10.1.2 事件的关系和运算 教学设计(表格式)
文档属性
| 名称 | 10.1.2 事件的关系和运算 教学设计(表格式) |  | |
| 格式 | docx | ||
| 文件大小 | 219.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-14 15:46:13 | ||
图片预览



文档简介
教学设计
课题 10.1.2事件的关系和运算
课型 新授课
教学内容分析 事件的关系与运算是继随机事件的后续部分,本节课提出了事件的关系、事件的运算等两部分学生将通过新旧知识的对比学习来进行自主学习,同时通过共同探讨来理解和掌握新知识的实际含义. 本节课应高度关注: 1.从具体的实力出发,让学生经历从特殊到一般、从具体到抽象的问题研究过程; 2.运用类比的方法把集合的关系和运算运用到事件的关系和运算上; 3.互斥事件和对立事件事件的关系,避免引起混淆.
学习目标确定 1.了解随机事件的并、交与互斥的含义,能结合实例进行随机事件的并、交运算 2.通过类比集合关系和运算,从而让学生更好的理解事件的关系和运算. 3.通过对事件的关系和运算的学习,培养学生数学抽象、数学运算、数学建模等数学素养.
学习重难点 重点:事件的包含、互斥、相互对立,并事件、交事件的含义; 难点:能进行随机事件的并、交运算,用简单事件表示复杂事件.
学习评价设计 针对我校学生的学习情况,我设计了三套评价表,主要从教师的课堂教学的评价、教师对学生课堂学习评价、学生课堂知识获得评价三个角度进行问卷调查来辅助敦师调整课堂教学. (1)学生对教师课堂教学的评价 从学生角度对教师的课堂教学进行评价,例如概念讲解清晰度、讲课速度、提问频率、做题留白等方面设计学生对教师课堂教学的评价量表,以便于老师对课堂教学进行反思和改进. 数学课堂教学评价表学习主题:4.1.1根式与分数指数幂项 目分值1.老师提出的问题比较清晰,我能听得很明白 1 2 3 4 52.老师在课堂中给了我们足够的谈论和分析时间 1 2 3 4 53.老师在整个课堂中经常会叫同学来谈谈对问题的看法 1 2 3 4 54.老师会叫同学去讲台上展示自己设计的方案 1 2 3 4 55.老师在课堂中多次下台走动听取大家的设计意见,并给予指导 1 2 3 4 56.整个课堂很有逻辑,问题进阶的很好 1 2 3 4 5给老师的课堂教学建议:
(2)学生课堂知识获得自我评价 大部分学生对自己课堂的学习获得会有一个比较准确的判断,而学生自我知识获得判断会与老师的反馈存在一定的偏差,而这个偏差对于一线教师有效诊断学生知识获得非常关键.有必要通过问卷或者课堂观测对学生进行知识获得自我感知的知识获得偏差诊断. 课堂学习评价项目分值1.今天数学课堂中老师讲的都听得很明白,记笔记清楚 ;1 2 3 4 52.了解事件的包含关系和相等关系;1 2 3 4 53.了解随机事件的并、交与互斥的含义;1 2 3 4 54.能结合具体实例进行随机事件的并、交运算;1 2 3 4 55.能从课堂中感受到事件关系和运算探究过过程培养我的数学抽象、数学运算.1 2 3 4 5小测1 1.在某高中的学生中任选一名学生,若事件A表示被选的学生是男生,事件B表示该生是高一的学生,事件C表示该生住宿的学生,则事件表示的含义是? 2.在某次随机试验的样本空间Ω={1,2,3,4,5,6,7,8},A=.则A∪B=______, 3.如何从集合的角度理解互斥事件和对立事件?
学习活动设计
教 师 活 动 学 生 活 动
环节一:创设情景 引入新课
我们来看一个很有意思但也很令人沮丧的事实:根据长期的观察和统计,一个人死于车祸的概率是1%;死于意外事故的概率是2%;死于呼吸道疾病的概率是5%;死于痴呆症的概率是10%;死于癌症的概率是20%;死于心脏病的概率是25%……假使这些疾病和事故不会同时发生在同一个人身上,虽然我们避开某种事故和疾病的概率是比较大的,但是避开所有疾病和事故的概率却是不容乐观的——不足20%! 当几个集合是有限集时,求集合A∪B与A∩B中元素的个数常用列举法列出集合中的元素. A∩B中元素的个数为即集合A与B中公共元素的个数;而当A∩B= 时,A∪B中元素的个数即为两个集合元素的个数之和;而当A∩B≠ 时,A∪B中元素的个数即为A,B中元素的个数之和减去A∩B中元素的个数. 从前面的学习中我们可以看到,我们在一个随机试验中可以定义许多随机事件.这些事件有的简单,有的复杂,我们希望从简单的事件的概率推算出复杂事件的概率,所以需要研究事件之间的关系和运算. 学生活动一 活动1:通过设计情景,引入本节新课。提高学生自主思考的能力,建立数学与生活实际的联系,提高学生的学习数学的兴趣. 活动2:复习回顾集合的交,并运算,并运用类比引入本节新。
环节二:事件的关系和运算
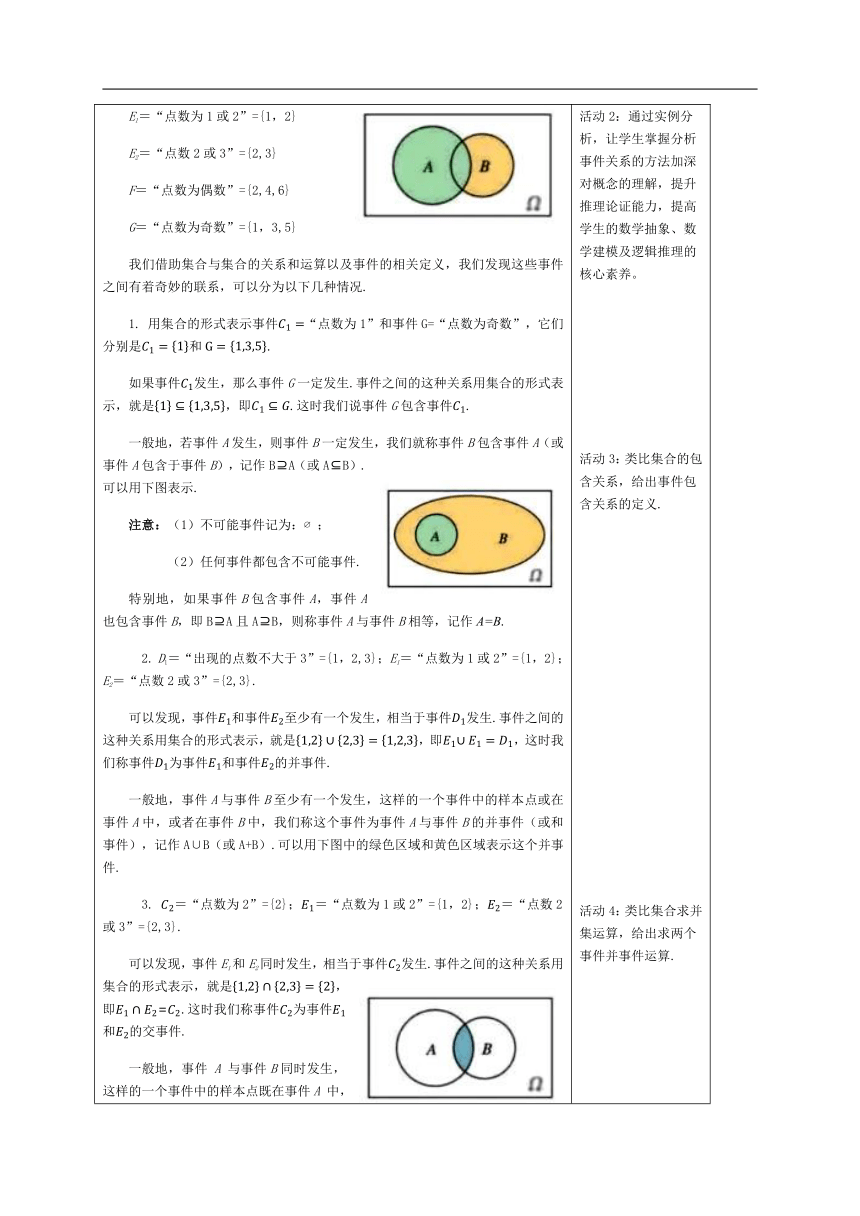
引例:在掷骰子试验中,观察骰子朝上面的点数,可以定义许多随机事件. 例如:Ci=“点数为i”,i=1,2,3,4,5,6 D1=“出现的点数不大于3”;D2=“点数大于3”;E1=“点数为1或2”,E2=“点数2或3”,F=“点数为偶数”,G=“点数为奇数”. 请用集合的形式表示这些事件,借助集合与集合的关系和运算,你能发现这些事件之间的联系么? 事实上,利用样本空间的的子集表示事件使我们可以利用集合的知识研究随机事件,从而为研究概率的性质和计算提供有效而简便的方法.下面我们按照这一思路展开研究: 我们把上述事件用集合的形式写出来得到下列集合 C1={1};C2={2};C3={3};C4={4};C5={5};C6={6}; D1=“出现的点数不大于3”={1,2,3} D2=“点数大于3”={4,5,6} E1=“点数为1或2”={1,2} E2=“点数2或3”={2,3} F=“点数为偶数”={2,4,6} G=“点数为奇数”={1,3,5} 我们借助集合与集合的关系和运算以及事件的相关定义,我们发现这些事件之间有着奇妙的联系,可以分为以下几种情况. 1. 用集合的形式表示事件“点数为1”和事件G=“点数为奇数”,它们分别是和. 如果事件发生,那么事件G一定发生.事件之间的这种关系用集合的形式表示,就是,即.这时我们说事件G包含事件. 一般地,若事件A发生,则事件B一定发生,我们就称事件B包含事件A(或事件A包含于事件B),记作B A(或A B).可以用下图表示. 注意:(1)不可能事件记为: ; (2)任何事件都包含不可能事件. 特别地,如果事件B包含事件A,事件A也包含事件B,即B A且A B,则称事件A与事件B相等,记作A=B. 2. D1=“出现的点数不大于3”={1,2,3};E1=“点数为1或2”={1,2};E2=“点数2或3”={2,3}. 可以发现,事件和事件至少有一个发生,相当于事件发生.事件之间的这种关系用集合的形式表示,就是,即,这时我们称事件为事件和事件的并事件. 一般地,事件A与事件B至少有一个发生,这样的一个事件中的样本点或在事件A中,或者在事件B中,我们称这个事件为事件A与事件B的并事件(或和事件),记作A∪B(或A+B).可以用下图中的绿色区域和黄色区域表示这个并事件. 3. =“点数为2”={2};=“点数为1或2”={1,2};=“点数2或3”={2,3}. 可以发现,事件E1和E2同时发生,相当于事件发生.事件之间的这种关系用集合的形式表示,就是,即=.这时我们称事件为事件和的交事件. 一般地,事件 A 与事件B同时发生,这样的一个事件中的样本点既在事件A 中,也在事件B中,我们称这样的一个事件为事件A 与事件B的交事件(或积事件),记作A∩B(或AB).可以用下图中的蓝色区域表示这个交事件. 4. 用集合的形式表示事件=“点数为3”和事件=“点数为4”,它们分别是=,=. 显然,事件与事件不可能同时发生,用集合的形式表示这种关系,就是,即,这时我们称事件与事件互斥. 一般地,如果事件A 与事件B不能同时发生,也就是说AB是一个不可能事件,即AB=,则称事件A与事件B互斥(或互不相容).可以用下图表示这两个事件互斥. 其含义是事件A与事件B在任何一次实验中不会同时发生. 5. 用集合的形式表示事件F=“点数为偶数”、事件G=“点数为奇数”,它们分别是,. 在任何一次试验中,事件F与事件G两者只能发生其中之一,而且也必然发生其中之一.事件之间的这种关系,用集合的形式可以表示为,即F=Ω,且,即F=.此时我们称事件F与事件G互为对立事件.事件 与 也有这种关系. 一般地,如果事件A和事件B在任何一次试验中有且仅有一个发生,即,且A=,那么称事件A与事件B互为对立.事件A的对立事件记为,可以用下图表示. 其含义是事件A与事件在任何一次实验中有且仅有一个发生. 总结:事件的关系或运算的含义,以及相应的符号表示如下: 事件的关系或运算含义符号表示包含A发生导致B发生并事件(和事件)A与B至少一个发生A∪B或A+B交事件(积事件)A与B同时发生A∩B或AB互斥(互不相容)A与B不能同时发生A∩B= 互为对立A与B有且仅有一个发生A=,
类似地,我们可以定义多个事件的和事件以及积事件.例如,对于三个事件A,B,C,A∪B∪C(A+B+C)发生当且仅当A,B,C中至少有一个发生,A∩B∩C(或ABC)发生当且仅当A,B,C同时发生,等等. 学生活动二 活动1:通过问题串的引导,思考问题,总结集合运算的定义。提高学生的分析问题、总结问题的能力。 活动2:通过实例分析,让学生掌握分析事件关系的方法加深对概念的理解,提升推理论证能力,提高学生的数学抽象、数学建模及逻辑推理的核心素养。 活动3:类比集合的包含关系,给出事件包含关系的定义. 活动4:类比集合求并集运算,给出求两个事件并事件运算. 活动5:类比集合求交集运算,给出求两个事件交事件运算. 活动6:类比两个集合交集运算,给出求两个事件互斥定义. 活动7:类比补集定义,给出求两个事件互为对立事件定义. 活动8 :通过表格汇总事件的定义,提高学生的分析问题、总结问题的能力。
环节三:例题讲解
例5 如图,由甲、乙两个元件组成一个并联电路,每个元件可能正常或失效.设事件A=“甲元件正常”,B=“乙元件正常”. (1)写出表示两个元件工作状态的样本空间; (2)用集合的形式表示事件A,B以及它们的对立事件; (3)用集合的形式表示事件A∪B和事件,并说明它们的含义及关系. 分析:注意到实验由甲、乙两个元件的状态组成,所以可以用数组(x1,x2)表示样本点.这样,确定事件A,B所包含的样本点时,不仅要考虑甲原件的状态 ,还要考虑乙原件的状态. 解:(1)用分别表示甲、乙两个元件的状态,则可以用表示这个并联电路的状态.以1表示元件正常,0表示元件失效,则样本空间为. 根据题意,可得,,. . (3).= 表示电路工作正常,表示电路工作不正常;和互为对立事件. 例 6一个袋子中有大小和质地相同的4个球,其中有有2个红色球(标号为1和2),2个绿色球(标号为3和4),从袋中不放回地依次随机摸出2个球设事件 =“第一次摸到红球”,=“第二次摸到红球”,R=“两次都摸到红球”,G=“两次都摸到绿球”,M=“两个球颜色相同”,N=“两个球颜色不同”. (1)用集合的形式分别写出试验的样本空间以及上述各事件; (2)事件R与 R1 ,R与G,M与N之间各有什么关系? (3)事件R与事件G的并事件与事件M有什么关系?事件 与事件的交事件与事件R有什么关系? 【解析】(1)所有的试验结果如图所示, 用数组表示可能的结果,是第一次摸到的球的标号,是第二次摸到的球的标号,则试验的样本空间= 事件R1=“第一次摸到红球”,即=1或2,于是 ; 事件=“第二次摸到红球”,即=1或2,于是. 同理,有 (2)因为,所以事件包含事件R; 因为R∩G= ,所以事件R与事件G互斥; 因为,所以事件M与事件N互为对立事件. (3)因为R∪G=M,所以事件M是事件R与事件G的并事件; 因为∩=R,所以事件R是事件与事件的交事件. 学生活动三 活动1:通过例5,让学生掌握怎样进行事件的运算,提高学生解决问题的能力。 活动2:通过例 6本,提高学生解决问题的能力,感悟其中蕴含的数学思想,增强学生的应用意识。
设计意图:从数与形两个角度呈现用逼近思想与极限思想,形象直观.
环节四: 课堂小结
(1)包含关系、相等关系的判定 ①事件的包含关系与集合的报刊关系相似; ②两事件相等的实质为相同事件,即同时发生或者同时不发生. (2)判断事件是否互斥的两个步骤 第一步,确定每个事件包含的结果; 第二步,确定是否有一个结果发生意味着两个事件都发生,若是,则两个事件不互斥,否则就是互斥的. (3)判断事件是否对立的两个步骤 第一步,判断是互斥事件; 第二步,确定两个事件必然有一个发生,否则只有互斥,但不对立. (4)事件的关系或运算的含义,以及相应的符号表示 事件的关系或运算含义符号表示包含A发生导致B发生并事件(和事件)A与B至少一个发生A∪B或A+B交事件(积事件)A与B同时发生A∩B或AB互斥(互不相容)A与B不能同时发生A∩B= 互为对立A与B有且仅有一个发生A=,
学生活动四 活动1:有理数指数幂的拓展 活动2:独立结题,有理数指数幂的运算
板书设计 10.1.2 事件的关系和运算 事件的关系或运算含义符号表示包含A发生导致B发生并事件(和事件)A与B至少一个发生A∪B或A+B交事件(积事件)A与B同时发生A∩B或AB互斥(互不相容)A与B不能同时发生A∩B= 互为对立A与B有且仅有一个发生A=,
课题 10.1.2事件的关系和运算
课型 新授课
教学内容分析 事件的关系与运算是继随机事件的后续部分,本节课提出了事件的关系、事件的运算等两部分学生将通过新旧知识的对比学习来进行自主学习,同时通过共同探讨来理解和掌握新知识的实际含义. 本节课应高度关注: 1.从具体的实力出发,让学生经历从特殊到一般、从具体到抽象的问题研究过程; 2.运用类比的方法把集合的关系和运算运用到事件的关系和运算上; 3.互斥事件和对立事件事件的关系,避免引起混淆.
学习目标确定 1.了解随机事件的并、交与互斥的含义,能结合实例进行随机事件的并、交运算 2.通过类比集合关系和运算,从而让学生更好的理解事件的关系和运算. 3.通过对事件的关系和运算的学习,培养学生数学抽象、数学运算、数学建模等数学素养.
学习重难点 重点:事件的包含、互斥、相互对立,并事件、交事件的含义; 难点:能进行随机事件的并、交运算,用简单事件表示复杂事件.
学习评价设计 针对我校学生的学习情况,我设计了三套评价表,主要从教师的课堂教学的评价、教师对学生课堂学习评价、学生课堂知识获得评价三个角度进行问卷调查来辅助敦师调整课堂教学. (1)学生对教师课堂教学的评价 从学生角度对教师的课堂教学进行评价,例如概念讲解清晰度、讲课速度、提问频率、做题留白等方面设计学生对教师课堂教学的评价量表,以便于老师对课堂教学进行反思和改进. 数学课堂教学评价表学习主题:4.1.1根式与分数指数幂项 目分值1.老师提出的问题比较清晰,我能听得很明白 1 2 3 4 52.老师在课堂中给了我们足够的谈论和分析时间 1 2 3 4 53.老师在整个课堂中经常会叫同学来谈谈对问题的看法 1 2 3 4 54.老师会叫同学去讲台上展示自己设计的方案 1 2 3 4 55.老师在课堂中多次下台走动听取大家的设计意见,并给予指导 1 2 3 4 56.整个课堂很有逻辑,问题进阶的很好 1 2 3 4 5给老师的课堂教学建议:
(2)学生课堂知识获得自我评价 大部分学生对自己课堂的学习获得会有一个比较准确的判断,而学生自我知识获得判断会与老师的反馈存在一定的偏差,而这个偏差对于一线教师有效诊断学生知识获得非常关键.有必要通过问卷或者课堂观测对学生进行知识获得自我感知的知识获得偏差诊断. 课堂学习评价项目分值1.今天数学课堂中老师讲的都听得很明白,记笔记清楚 ;1 2 3 4 52.了解事件的包含关系和相等关系;1 2 3 4 53.了解随机事件的并、交与互斥的含义;1 2 3 4 54.能结合具体实例进行随机事件的并、交运算;1 2 3 4 55.能从课堂中感受到事件关系和运算探究过过程培养我的数学抽象、数学运算.1 2 3 4 5小测1 1.在某高中的学生中任选一名学生,若事件A表示被选的学生是男生,事件B表示该生是高一的学生,事件C表示该生住宿的学生,则事件表示的含义是? 2.在某次随机试验的样本空间Ω={1,2,3,4,5,6,7,8},A=.则A∪B=______, 3.如何从集合的角度理解互斥事件和对立事件?
学习活动设计
教 师 活 动 学 生 活 动
环节一:创设情景 引入新课
我们来看一个很有意思但也很令人沮丧的事实:根据长期的观察和统计,一个人死于车祸的概率是1%;死于意外事故的概率是2%;死于呼吸道疾病的概率是5%;死于痴呆症的概率是10%;死于癌症的概率是20%;死于心脏病的概率是25%……假使这些疾病和事故不会同时发生在同一个人身上,虽然我们避开某种事故和疾病的概率是比较大的,但是避开所有疾病和事故的概率却是不容乐观的——不足20%! 当几个集合是有限集时,求集合A∪B与A∩B中元素的个数常用列举法列出集合中的元素. A∩B中元素的个数为即集合A与B中公共元素的个数;而当A∩B= 时,A∪B中元素的个数即为两个集合元素的个数之和;而当A∩B≠ 时,A∪B中元素的个数即为A,B中元素的个数之和减去A∩B中元素的个数. 从前面的学习中我们可以看到,我们在一个随机试验中可以定义许多随机事件.这些事件有的简单,有的复杂,我们希望从简单的事件的概率推算出复杂事件的概率,所以需要研究事件之间的关系和运算. 学生活动一 活动1:通过设计情景,引入本节新课。提高学生自主思考的能力,建立数学与生活实际的联系,提高学生的学习数学的兴趣. 活动2:复习回顾集合的交,并运算,并运用类比引入本节新。
环节二:事件的关系和运算
引例:在掷骰子试验中,观察骰子朝上面的点数,可以定义许多随机事件. 例如:Ci=“点数为i”,i=1,2,3,4,5,6 D1=“出现的点数不大于3”;D2=“点数大于3”;E1=“点数为1或2”,E2=“点数2或3”,F=“点数为偶数”,G=“点数为奇数”. 请用集合的形式表示这些事件,借助集合与集合的关系和运算,你能发现这些事件之间的联系么? 事实上,利用样本空间的的子集表示事件使我们可以利用集合的知识研究随机事件,从而为研究概率的性质和计算提供有效而简便的方法.下面我们按照这一思路展开研究: 我们把上述事件用集合的形式写出来得到下列集合 C1={1};C2={2};C3={3};C4={4};C5={5};C6={6}; D1=“出现的点数不大于3”={1,2,3} D2=“点数大于3”={4,5,6} E1=“点数为1或2”={1,2} E2=“点数2或3”={2,3} F=“点数为偶数”={2,4,6} G=“点数为奇数”={1,3,5} 我们借助集合与集合的关系和运算以及事件的相关定义,我们发现这些事件之间有着奇妙的联系,可以分为以下几种情况. 1. 用集合的形式表示事件“点数为1”和事件G=“点数为奇数”,它们分别是和. 如果事件发生,那么事件G一定发生.事件之间的这种关系用集合的形式表示,就是,即.这时我们说事件G包含事件. 一般地,若事件A发生,则事件B一定发生,我们就称事件B包含事件A(或事件A包含于事件B),记作B A(或A B).可以用下图表示. 注意:(1)不可能事件记为: ; (2)任何事件都包含不可能事件. 特别地,如果事件B包含事件A,事件A也包含事件B,即B A且A B,则称事件A与事件B相等,记作A=B. 2. D1=“出现的点数不大于3”={1,2,3};E1=“点数为1或2”={1,2};E2=“点数2或3”={2,3}. 可以发现,事件和事件至少有一个发生,相当于事件发生.事件之间的这种关系用集合的形式表示,就是,即,这时我们称事件为事件和事件的并事件. 一般地,事件A与事件B至少有一个发生,这样的一个事件中的样本点或在事件A中,或者在事件B中,我们称这个事件为事件A与事件B的并事件(或和事件),记作A∪B(或A+B).可以用下图中的绿色区域和黄色区域表示这个并事件. 3. =“点数为2”={2};=“点数为1或2”={1,2};=“点数2或3”={2,3}. 可以发现,事件E1和E2同时发生,相当于事件发生.事件之间的这种关系用集合的形式表示,就是,即=.这时我们称事件为事件和的交事件. 一般地,事件 A 与事件B同时发生,这样的一个事件中的样本点既在事件A 中,也在事件B中,我们称这样的一个事件为事件A 与事件B的交事件(或积事件),记作A∩B(或AB).可以用下图中的蓝色区域表示这个交事件. 4. 用集合的形式表示事件=“点数为3”和事件=“点数为4”,它们分别是=,=. 显然,事件与事件不可能同时发生,用集合的形式表示这种关系,就是,即,这时我们称事件与事件互斥. 一般地,如果事件A 与事件B不能同时发生,也就是说AB是一个不可能事件,即AB=,则称事件A与事件B互斥(或互不相容).可以用下图表示这两个事件互斥. 其含义是事件A与事件B在任何一次实验中不会同时发生. 5. 用集合的形式表示事件F=“点数为偶数”、事件G=“点数为奇数”,它们分别是,. 在任何一次试验中,事件F与事件G两者只能发生其中之一,而且也必然发生其中之一.事件之间的这种关系,用集合的形式可以表示为,即F=Ω,且,即F=.此时我们称事件F与事件G互为对立事件.事件 与 也有这种关系. 一般地,如果事件A和事件B在任何一次试验中有且仅有一个发生,即,且A=,那么称事件A与事件B互为对立.事件A的对立事件记为,可以用下图表示. 其含义是事件A与事件在任何一次实验中有且仅有一个发生. 总结:事件的关系或运算的含义,以及相应的符号表示如下: 事件的关系或运算含义符号表示包含A发生导致B发生并事件(和事件)A与B至少一个发生A∪B或A+B交事件(积事件)A与B同时发生A∩B或AB互斥(互不相容)A与B不能同时发生A∩B= 互为对立A与B有且仅有一个发生A=,
类似地,我们可以定义多个事件的和事件以及积事件.例如,对于三个事件A,B,C,A∪B∪C(A+B+C)发生当且仅当A,B,C中至少有一个发生,A∩B∩C(或ABC)发生当且仅当A,B,C同时发生,等等. 学生活动二 活动1:通过问题串的引导,思考问题,总结集合运算的定义。提高学生的分析问题、总结问题的能力。 活动2:通过实例分析,让学生掌握分析事件关系的方法加深对概念的理解,提升推理论证能力,提高学生的数学抽象、数学建模及逻辑推理的核心素养。 活动3:类比集合的包含关系,给出事件包含关系的定义. 活动4:类比集合求并集运算,给出求两个事件并事件运算. 活动5:类比集合求交集运算,给出求两个事件交事件运算. 活动6:类比两个集合交集运算,给出求两个事件互斥定义. 活动7:类比补集定义,给出求两个事件互为对立事件定义. 活动8 :通过表格汇总事件的定义,提高学生的分析问题、总结问题的能力。
环节三:例题讲解
例5 如图,由甲、乙两个元件组成一个并联电路,每个元件可能正常或失效.设事件A=“甲元件正常”,B=“乙元件正常”. (1)写出表示两个元件工作状态的样本空间; (2)用集合的形式表示事件A,B以及它们的对立事件; (3)用集合的形式表示事件A∪B和事件,并说明它们的含义及关系. 分析:注意到实验由甲、乙两个元件的状态组成,所以可以用数组(x1,x2)表示样本点.这样,确定事件A,B所包含的样本点时,不仅要考虑甲原件的状态 ,还要考虑乙原件的状态. 解:(1)用分别表示甲、乙两个元件的状态,则可以用表示这个并联电路的状态.以1表示元件正常,0表示元件失效,则样本空间为. 根据题意,可得,,. . (3).= 表示电路工作正常,表示电路工作不正常;和互为对立事件. 例 6一个袋子中有大小和质地相同的4个球,其中有有2个红色球(标号为1和2),2个绿色球(标号为3和4),从袋中不放回地依次随机摸出2个球设事件 =“第一次摸到红球”,=“第二次摸到红球”,R=“两次都摸到红球”,G=“两次都摸到绿球”,M=“两个球颜色相同”,N=“两个球颜色不同”. (1)用集合的形式分别写出试验的样本空间以及上述各事件; (2)事件R与 R1 ,R与G,M与N之间各有什么关系? (3)事件R与事件G的并事件与事件M有什么关系?事件 与事件的交事件与事件R有什么关系? 【解析】(1)所有的试验结果如图所示, 用数组表示可能的结果,是第一次摸到的球的标号,是第二次摸到的球的标号,则试验的样本空间= 事件R1=“第一次摸到红球”,即=1或2,于是 ; 事件=“第二次摸到红球”,即=1或2,于是. 同理,有 (2)因为,所以事件包含事件R; 因为R∩G= ,所以事件R与事件G互斥; 因为,所以事件M与事件N互为对立事件. (3)因为R∪G=M,所以事件M是事件R与事件G的并事件; 因为∩=R,所以事件R是事件与事件的交事件. 学生活动三 活动1:通过例5,让学生掌握怎样进行事件的运算,提高学生解决问题的能力。 活动2:通过例 6本,提高学生解决问题的能力,感悟其中蕴含的数学思想,增强学生的应用意识。
设计意图:从数与形两个角度呈现用逼近思想与极限思想,形象直观.
环节四: 课堂小结
(1)包含关系、相等关系的判定 ①事件的包含关系与集合的报刊关系相似; ②两事件相等的实质为相同事件,即同时发生或者同时不发生. (2)判断事件是否互斥的两个步骤 第一步,确定每个事件包含的结果; 第二步,确定是否有一个结果发生意味着两个事件都发生,若是,则两个事件不互斥,否则就是互斥的. (3)判断事件是否对立的两个步骤 第一步,判断是互斥事件; 第二步,确定两个事件必然有一个发生,否则只有互斥,但不对立. (4)事件的关系或运算的含义,以及相应的符号表示 事件的关系或运算含义符号表示包含A发生导致B发生并事件(和事件)A与B至少一个发生A∪B或A+B交事件(积事件)A与B同时发生A∩B或AB互斥(互不相容)A与B不能同时发生A∩B= 互为对立A与B有且仅有一个发生A=,
学生活动四 活动1:有理数指数幂的拓展 活动2:独立结题,有理数指数幂的运算
板书设计 10.1.2 事件的关系和运算 事件的关系或运算含义符号表示包含A发生导致B发生并事件(和事件)A与B至少一个发生A∪B或A+B交事件(积事件)A与B同时发生A∩B或AB互斥(互不相容)A与B不能同时发生A∩B= 互为对立A与B有且仅有一个发生A=,
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
