2024-2025学年上海市华东师范大学附属周浦中学高一下学期3月月考数学试卷(含答案)
文档属性
| 名称 | 2024-2025学年上海市华东师范大学附属周浦中学高一下学期3月月考数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 77.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-13 12:53:54 | ||
图片预览


文档简介
2024-2025学年上海市华东师范大学附属周浦中学高一下学期3月月考数学试卷
一、单选题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知是的内角,则“”是“”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
2.已知点,将线段绕坐标原点逆时针转动至,则点的纵坐标为( )
A. B. C. D.
3.若,则的值为
A. B. C. D.
4.如图,等腰是上一点,、的外接圆半径分别为、,则的值为 .
A. B. C. D. 由点的位置确定
二、填空题:本题共12小题,每小题5分,共60分。
5.与终边相同的角的集合是 .
6.弧度是第 象限角.
7.已知扇形的半径为,圆心角为,则扇形的弧长为 .
8.已知,则 .
9.若,则点在第 象限.
10.要使有意义,则的取值范围为 .
11.已知运算:,若,则 .
12.方程在上的解 .
13.已知,则 .
14.已知锐角,满足,则 .
15.已知命题:
若,则;
若,则;
若,则必定是第一或者第二象限角;
若是第一或者第二象限角,则.
则上述命题是真命题的个数为 .
16.已知函数,若,,则 .
三、解答题:本题共5小题,共70分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
已知角的终边过点.
求的值;
若角与角的终边关于轴对称,求.
18.本小题分
已知在中,三个内角所对的边分别为.
当时,求用反余弦表示.
当,时,的面积为,求的值.
19.本小题分
已知,求下列各式的值:
20.本小题分
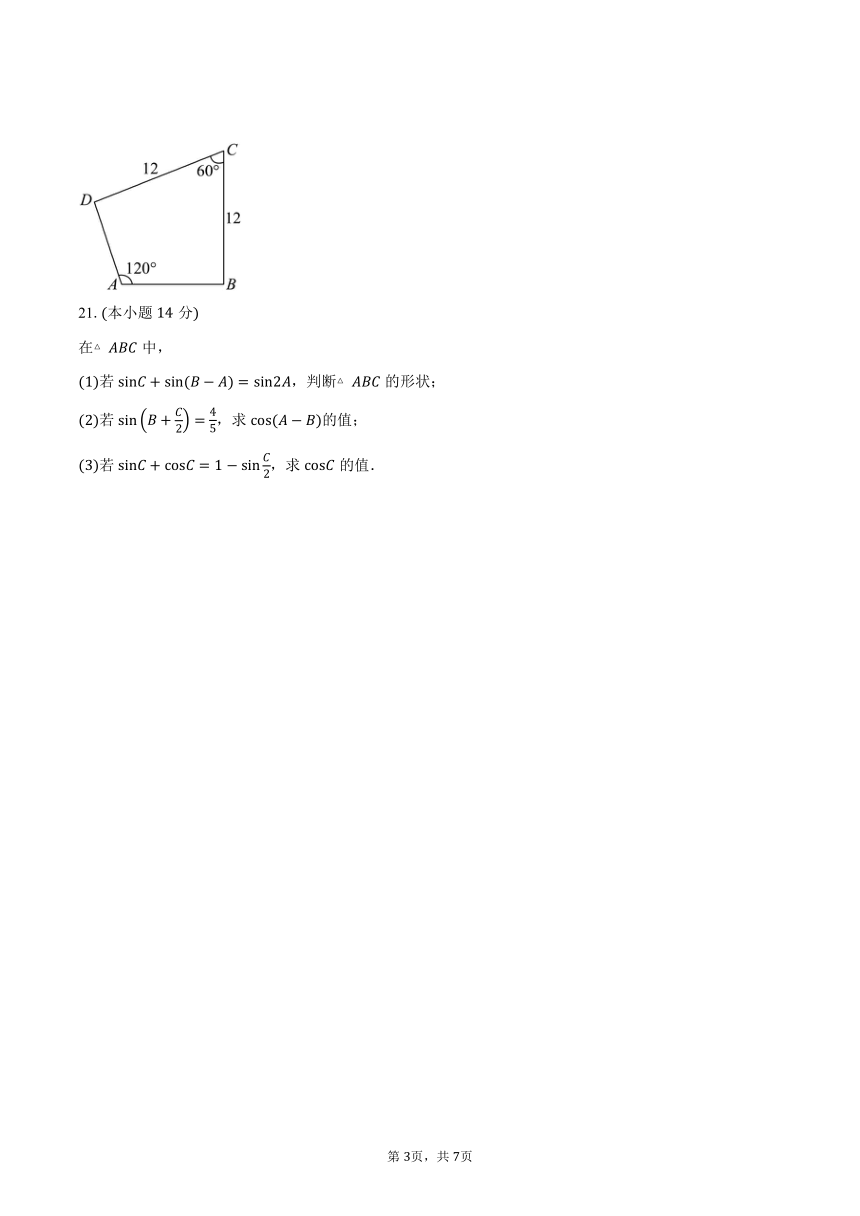
某校学生在学农期间参观了某农村的蔬菜园地,已知该农村中某块蔬菜园地的形状为如图所示的四边形,经测量,边界,,.
若的长为,求的长;
现需要沿该园地的边界修建篱笆不计宽度以提醒同学们不要随意进入该园地,问所需要的篱笆的最大长度为多少米?提示:设
21.本小题分
在中,
若,判断的形状;
若,求的值;
若,求的值.
参考答案
1.
2.
3.
4.
5.
6.三
7.或
8.或
9.二
10.
11.
12.
13.
14.
15.
16.
17.解:因为角的终边过点,
可知角的终边在第一象限,且,
则.
因为角和角的终边关于轴对称,且,
所以,
因为角的终边在第一象限,所以在第四象限,所以
18.解:由正弦定理和,可得,不妨设,则,
由余弦定理,,
故,则.
因,,且的面积为,
由,可得,
因,故或.
当时,由余弦定理,;
当时,由余弦定理,.
故的值为或.
19.解:若,则不符合题意,故,
则由可得,得;
;
20.解:由题意可知为等边三角形,即,
在中利用余弦定理得,
即,解得;
设,且,
则在中利用正弦定理得,
即,
则
,
因,则,结合正弦函数图象可知,,
则,故
则所需要的篱笆的最大长度为
21.解:因为,
又因为,
所以,
所以,
所以,
所以或,
所以或由正弦定理得,
所以为直角三角形或等腰三角形.
因为,所以,
所以
所以.
因为为三角形内角,所以,即
所以
平方得
因为,
所以
所以可得,即
则.
第1页,共1页
一、单选题:本题共4小题,每小题5分,共20分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知是的内角,则“”是“”的( )
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
2.已知点,将线段绕坐标原点逆时针转动至,则点的纵坐标为( )
A. B. C. D.
3.若,则的值为
A. B. C. D.
4.如图,等腰是上一点,、的外接圆半径分别为、,则的值为 .
A. B. C. D. 由点的位置确定
二、填空题:本题共12小题,每小题5分,共60分。
5.与终边相同的角的集合是 .
6.弧度是第 象限角.
7.已知扇形的半径为,圆心角为,则扇形的弧长为 .
8.已知,则 .
9.若,则点在第 象限.
10.要使有意义,则的取值范围为 .
11.已知运算:,若,则 .
12.方程在上的解 .
13.已知,则 .
14.已知锐角,满足,则 .
15.已知命题:
若,则;
若,则;
若,则必定是第一或者第二象限角;
若是第一或者第二象限角,则.
则上述命题是真命题的个数为 .
16.已知函数,若,,则 .
三、解答题:本题共5小题,共70分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
已知角的终边过点.
求的值;
若角与角的终边关于轴对称,求.
18.本小题分
已知在中,三个内角所对的边分别为.
当时,求用反余弦表示.
当,时,的面积为,求的值.
19.本小题分
已知,求下列各式的值:
20.本小题分
某校学生在学农期间参观了某农村的蔬菜园地,已知该农村中某块蔬菜园地的形状为如图所示的四边形,经测量,边界,,.
若的长为,求的长;
现需要沿该园地的边界修建篱笆不计宽度以提醒同学们不要随意进入该园地,问所需要的篱笆的最大长度为多少米?提示:设
21.本小题分
在中,
若,判断的形状;
若,求的值;
若,求的值.
参考答案
1.
2.
3.
4.
5.
6.三
7.或
8.或
9.二
10.
11.
12.
13.
14.
15.
16.
17.解:因为角的终边过点,
可知角的终边在第一象限,且,
则.
因为角和角的终边关于轴对称,且,
所以,
因为角的终边在第一象限,所以在第四象限,所以
18.解:由正弦定理和,可得,不妨设,则,
由余弦定理,,
故,则.
因,,且的面积为,
由,可得,
因,故或.
当时,由余弦定理,;
当时,由余弦定理,.
故的值为或.
19.解:若,则不符合题意,故,
则由可得,得;
;
20.解:由题意可知为等边三角形,即,
在中利用余弦定理得,
即,解得;
设,且,
则在中利用正弦定理得,
即,
则
,
因,则,结合正弦函数图象可知,,
则,故
则所需要的篱笆的最大长度为
21.解:因为,
又因为,
所以,
所以,
所以,
所以或,
所以或由正弦定理得,
所以为直角三角形或等腰三角形.
因为,所以,
所以
所以.
因为为三角形内角,所以,即
所以
平方得
因为,
所以
所以可得,即
则.
第1页,共1页
同课章节目录
