2024-2025学年北京166中学高二(下)段考数学试卷(3月份)(含答案)
文档属性
| 名称 | 2024-2025学年北京166中学高二(下)段考数学试卷(3月份)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 374.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-14 12:24:23 | ||
图片预览




文档简介
2024-2025学年北京166中学高二(下)3月段考
数学试卷
一、单选题:本题共10小题,每小题4分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.若直线:与直线:垂直,则实数为( )
A. B. C. D.
2.下列求导运算中,正确的一项是( )
A. B.
C. D.
3.某家新能源电池制造企业拥有两类生产线,分别生产高能量密度锂电池和低能量密度锂电池,两条线的日总产量为支锂电池,质检人员按两类生产线的产量比例采用分层抽样方法随机抽取一个容量为的样本进行质量检测,已知样本中高能量密度锂电池有支,则低能量密度锂电池的日产量为( )
A. 支 B. 支 C. 支 D. 支
4.的展开式中常数项为( )
A. B. C. D.
5.已知函数的定义域为,且的图象是一条连续不断的曲线,的导函数为若函数的图象如图所示,则( )
A. 在区间上单调递增
B. 在区间上单调递减
C.
D.
6.双曲线,点,则直线与双曲线的公共点的个数( )
A. 个 B. 恰有个 C. 恰有个 D. 恰有个
7.设定义在上的函数,,导函数分别为,,则“”是“”的( )
A. 充分而不必要条件 B. 必要而不充分条件
C. 充要条件 D. 既不充分也不必要条件
8.将名志愿者随机分配到个项目卫生、宣传、审计服务,卫生项目与宣传项目各分配名志愿者,审计项目只需名志愿者,则不同的分配方案共有( )
A. 种 B. 种 C. 种 D. 种
9.平面直角坐标系中,双曲线:的两条渐近线与抛物线:交于,,三点,若的垂心为的焦点,则的离心率为( )
A. B. C. D.
10.甲抛掷均匀硬币次,乙抛掷均匀硬币次,下列四个随机事件的概率是的是( )
甲抛出正面次数比乙抛出正面次数多.
甲抛出反面次数比乙抛出正面次数少.
甲抛出反面次数比甲抛出正面次数多.
乙抛出正面次数与乙抛出反面次数一样多.
A. B. C. D.
二、填空题:本题共6小题,共50分。
11.展开式的二项式系数和为______, ______用数字作答
12.若,则 ______;
若,则 ______.
13.某雪堆在融化过程中,其体积单位:与融化时间单位:近似满足函数关系:为常数,其图象如图所示.
设,从到的雪堆体积的平均变化率的值为______;
记时雪堆融化的瞬时速度为,时雪堆融化的瞬时速度为,则的值为______.
14.从甲、乙等名志愿者中选出名,分别从事,,,四项不同的工作,每人承担一项且甲、乙均不从事工作,则不同的工作分配方案共有______种
15.意大利画家列奥纳多达芬奇的画作抱银貂的女人中,女士脖颈上黑色珍珠项链与主人相互映衬呈现出不一样的美与光泽,达芬奇提出:一条粗细与质量分布均匀的项链,其长度不能自然伸缩,固定其两端,使其受重力作用自然下垂,项链所形成的曲线是什么?这就是著名的“悬链线问题”约翰伯努利给出了悬链线的函数解析式:,其中为悬链线系数,是曲线顶点到横坐标轴的距离并且由此数学世界中产生了一类新的函数:双曲函数包括双曲正弦函数,双曲余弦函数.
可见,悬链线的函数解析式恰好是 ______填或者之一.
若双曲正弦函数在点处的切线的斜率为,双曲余弦函数在点处的切线平行于轴,与相交于点,则的周长为______.
16.若双曲正弦函数在点处的切线的斜率为,双曲余弦函数在点处的切线平行于轴,与相交于点,则的周长为______.
三、解答题:本题共6小题,共60分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
已知函数.
求曲线在点处的切线方程;
求曲线过点处的切线方程.
18.本小题分
一个不透明的袋子中,放有大小相同的个小球,其中个黑球,个白球回答下列问题:
从袋中随机不放回地取出个球,求其中恰好有两个黑球的概率;
从袋中有放回地依次随机取球,每次取一个球,共取三次,求恰有两次取得黑球的概率;
从袋中不放回地随机取球,每次取一个球,共取两次,求第二次取出黑球的概率.
19.本小题分
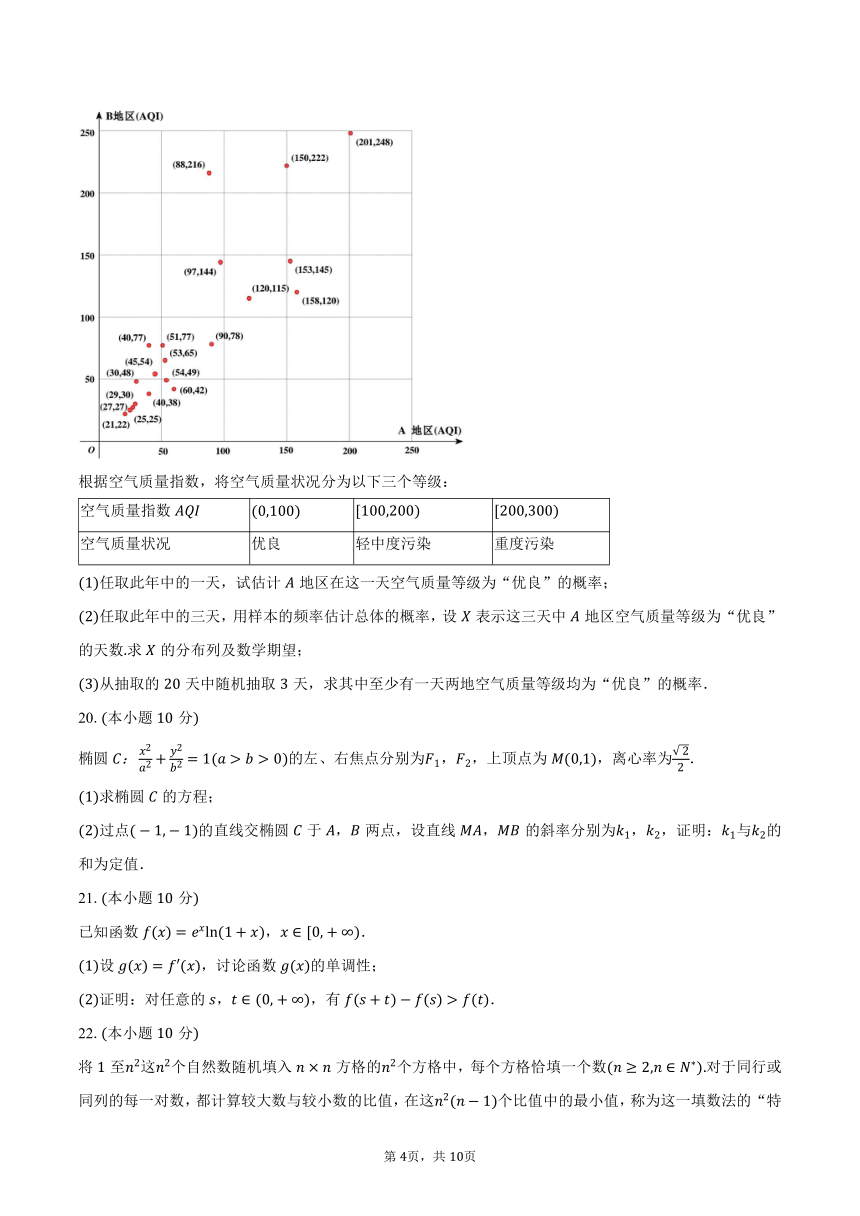
为评估大气污染防治效果,调查区域空气质量状况,某调研机构从同一年,两地区的空气质量指数数据中随机抽取相同天的观测数据,形成个有序数对分别为同一天,两地的空气质量指数,如图所示:
根据空气质量指数,将空气质量状况分为以下三个等级:
空气质量指数
空气质量状况 优良 轻中度污染 重度污染
任取此年中的一天,试估计地区在这一天空气质量等级为“优良”的概率;
任取此年中的三天,用样本的频率估计总体的概率,设表示这三天中地区空气质量等级为“优良”的天数求的分布列及数学期望;
从抽取的天中随机抽取天,求其中至少有一天两地空气质量等级均为“优良”的概率.
20.本小题分
椭圆的左、右焦点分别为,,上顶点为,离心率为.
求椭圆的方程;
过点的直线交椭圆于,两点,设直线,的斜率分别为,,证明:与的和为定值.
21.本小题分
已知函数,.
设,讨论函数的单调性;
证明:对任意的,,有.
22.本小题分
将至这个自然数随机填入方格的个方格中,每个方格恰填一个数对于同行或同列的每一对数,都计算较大数与较小数的比值,在这个比值中的最小值,称为这一填数法的“特征值”.
Ⅰ若,请写出一种填数法,并计算此填数法的“特征值”;
Ⅱ当时,请写出一种填数法,使得此填数法的“特征值”为;
Ⅲ求证:对任意一个填数法,其“特征值”不大于.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.解:因为 ,所以 ,
所以,,
所以所求切线方程为,即;
设切点坐标为,且,由知,
由直线的点斜式方程可得切线方程为 ,
由切线经过点,代入可得,
化简得 ,解得 或,又,
结合切线过点可得切线的方程为 或.
18.解:从袋中随机不放回地取出个球,其中恰好有两个黑球的概率为;
从袋中每次取一个球,其为黑球的概率为,
则随机有放回地依次取球,每次取一个球,共取三次,
恰有两次取得黑球的概率为;
设第一次取白球为事件,则第一次取为黑球为,第二次取黑球为事件,
则,,,,
所以.
19.解:根据题意,由图表的数据,
从地区选出的天中随机选出一天,这一天空气质量状况为“优良”的频率为 ,
估计地区当年的空气质量状况“优良”的概率为.
根据题意,表示这三天中地区空气质量等级为“优良”的天数,
则,可取的值为、、、,
则,
,
,
,
所以的分布列为
故.
由图知,在抽取的天中,两地空气质量等级均为“优良”的有天,
至少有一天两地空气质量等级均为“优良”的对立事件是天没有任何一天两地空气质量等级均为“优良”,
所以从抽取的天中随机抽取天,至少有一天两地空气质量等级均为“优良”的概率
.
所以至少有一天两地空气质量等级均为“优良”的概率为.
20.解:根据题目:椭圆的左、右焦点分别为,,
上顶点为,离心率为得,
由椭圆的离心率为,得,解得,
所以椭圆的方程为:.
证明:由题:过点的直线交椭圆于,两点,设直线,的斜率分别为,,
当直线的斜率存在时,设其方程为,,,,
由消去得:,
,解得或,
,,
因此,
当直线斜率不存在时,由,得,
不妨令,则,
所以与的和为定值.
21.解:因为,,
所以,.
所以,
则,
令,
则,
当时,恒成立,则单调递增,
又,所以恒成立,
则在上恒成立,
所以在上单调递增;
证明:令,其中,,
可得,
由可知在上单调递增,且,,
有,即恒成立,
即在上单调递增,
则,
即对任意,恒成立.
22.解:Ⅰ当时,如下表填数:
同行或同列的每一对数,计算较大数与较小数的比值分别为
,,,,可得此填数法的“特征值”为;
Ⅱ当时,如下表填数:
同行或同列的每一对数,计算较大数与较小数的比值分别为
,,,,,,,,,,,,,,,,,,
可得此填数法的“特征值”为;
Ⅲ不妨设为任意一个填数法,记此填数法的“特征值”为,
考虑含个元素的集合,
易知其中必有至少两个数处于同一行,设为
也必有至少两个数处于同一列,设为.
若
则有因为
若,即,
则,.
所以.
即不论何种情况,总有.
第1页,共1页
数学试卷
一、单选题:本题共10小题,每小题4分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.若直线:与直线:垂直,则实数为( )
A. B. C. D.
2.下列求导运算中,正确的一项是( )
A. B.
C. D.
3.某家新能源电池制造企业拥有两类生产线,分别生产高能量密度锂电池和低能量密度锂电池,两条线的日总产量为支锂电池,质检人员按两类生产线的产量比例采用分层抽样方法随机抽取一个容量为的样本进行质量检测,已知样本中高能量密度锂电池有支,则低能量密度锂电池的日产量为( )
A. 支 B. 支 C. 支 D. 支
4.的展开式中常数项为( )
A. B. C. D.
5.已知函数的定义域为,且的图象是一条连续不断的曲线,的导函数为若函数的图象如图所示,则( )
A. 在区间上单调递增
B. 在区间上单调递减
C.
D.
6.双曲线,点,则直线与双曲线的公共点的个数( )
A. 个 B. 恰有个 C. 恰有个 D. 恰有个
7.设定义在上的函数,,导函数分别为,,则“”是“”的( )
A. 充分而不必要条件 B. 必要而不充分条件
C. 充要条件 D. 既不充分也不必要条件
8.将名志愿者随机分配到个项目卫生、宣传、审计服务,卫生项目与宣传项目各分配名志愿者,审计项目只需名志愿者,则不同的分配方案共有( )
A. 种 B. 种 C. 种 D. 种
9.平面直角坐标系中,双曲线:的两条渐近线与抛物线:交于,,三点,若的垂心为的焦点,则的离心率为( )
A. B. C. D.
10.甲抛掷均匀硬币次,乙抛掷均匀硬币次,下列四个随机事件的概率是的是( )
甲抛出正面次数比乙抛出正面次数多.
甲抛出反面次数比乙抛出正面次数少.
甲抛出反面次数比甲抛出正面次数多.
乙抛出正面次数与乙抛出反面次数一样多.
A. B. C. D.
二、填空题:本题共6小题,共50分。
11.展开式的二项式系数和为______, ______用数字作答
12.若,则 ______;
若,则 ______.
13.某雪堆在融化过程中,其体积单位:与融化时间单位:近似满足函数关系:为常数,其图象如图所示.
设,从到的雪堆体积的平均变化率的值为______;
记时雪堆融化的瞬时速度为,时雪堆融化的瞬时速度为,则的值为______.
14.从甲、乙等名志愿者中选出名,分别从事,,,四项不同的工作,每人承担一项且甲、乙均不从事工作,则不同的工作分配方案共有______种
15.意大利画家列奥纳多达芬奇的画作抱银貂的女人中,女士脖颈上黑色珍珠项链与主人相互映衬呈现出不一样的美与光泽,达芬奇提出:一条粗细与质量分布均匀的项链,其长度不能自然伸缩,固定其两端,使其受重力作用自然下垂,项链所形成的曲线是什么?这就是著名的“悬链线问题”约翰伯努利给出了悬链线的函数解析式:,其中为悬链线系数,是曲线顶点到横坐标轴的距离并且由此数学世界中产生了一类新的函数:双曲函数包括双曲正弦函数,双曲余弦函数.
可见,悬链线的函数解析式恰好是 ______填或者之一.
若双曲正弦函数在点处的切线的斜率为,双曲余弦函数在点处的切线平行于轴,与相交于点,则的周长为______.
16.若双曲正弦函数在点处的切线的斜率为,双曲余弦函数在点处的切线平行于轴,与相交于点,则的周长为______.
三、解答题:本题共6小题,共60分。解答应写出文字说明,证明过程或演算步骤。
17.本小题分
已知函数.
求曲线在点处的切线方程;
求曲线过点处的切线方程.
18.本小题分
一个不透明的袋子中,放有大小相同的个小球,其中个黑球,个白球回答下列问题:
从袋中随机不放回地取出个球,求其中恰好有两个黑球的概率;
从袋中有放回地依次随机取球,每次取一个球,共取三次,求恰有两次取得黑球的概率;
从袋中不放回地随机取球,每次取一个球,共取两次,求第二次取出黑球的概率.
19.本小题分
为评估大气污染防治效果,调查区域空气质量状况,某调研机构从同一年,两地区的空气质量指数数据中随机抽取相同天的观测数据,形成个有序数对分别为同一天,两地的空气质量指数,如图所示:
根据空气质量指数,将空气质量状况分为以下三个等级:
空气质量指数
空气质量状况 优良 轻中度污染 重度污染
任取此年中的一天,试估计地区在这一天空气质量等级为“优良”的概率;
任取此年中的三天,用样本的频率估计总体的概率,设表示这三天中地区空气质量等级为“优良”的天数求的分布列及数学期望;
从抽取的天中随机抽取天,求其中至少有一天两地空气质量等级均为“优良”的概率.
20.本小题分
椭圆的左、右焦点分别为,,上顶点为,离心率为.
求椭圆的方程;
过点的直线交椭圆于,两点,设直线,的斜率分别为,,证明:与的和为定值.
21.本小题分
已知函数,.
设,讨论函数的单调性;
证明:对任意的,,有.
22.本小题分
将至这个自然数随机填入方格的个方格中,每个方格恰填一个数对于同行或同列的每一对数,都计算较大数与较小数的比值,在这个比值中的最小值,称为这一填数法的“特征值”.
Ⅰ若,请写出一种填数法,并计算此填数法的“特征值”;
Ⅱ当时,请写出一种填数法,使得此填数法的“特征值”为;
Ⅲ求证:对任意一个填数法,其“特征值”不大于.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.解:因为 ,所以 ,
所以,,
所以所求切线方程为,即;
设切点坐标为,且,由知,
由直线的点斜式方程可得切线方程为 ,
由切线经过点,代入可得,
化简得 ,解得 或,又,
结合切线过点可得切线的方程为 或.
18.解:从袋中随机不放回地取出个球,其中恰好有两个黑球的概率为;
从袋中每次取一个球,其为黑球的概率为,
则随机有放回地依次取球,每次取一个球,共取三次,
恰有两次取得黑球的概率为;
设第一次取白球为事件,则第一次取为黑球为,第二次取黑球为事件,
则,,,,
所以.
19.解:根据题意,由图表的数据,
从地区选出的天中随机选出一天,这一天空气质量状况为“优良”的频率为 ,
估计地区当年的空气质量状况“优良”的概率为.
根据题意,表示这三天中地区空气质量等级为“优良”的天数,
则,可取的值为、、、,
则,
,
,
,
所以的分布列为
故.
由图知,在抽取的天中,两地空气质量等级均为“优良”的有天,
至少有一天两地空气质量等级均为“优良”的对立事件是天没有任何一天两地空气质量等级均为“优良”,
所以从抽取的天中随机抽取天,至少有一天两地空气质量等级均为“优良”的概率
.
所以至少有一天两地空气质量等级均为“优良”的概率为.
20.解:根据题目:椭圆的左、右焦点分别为,,
上顶点为,离心率为得,
由椭圆的离心率为,得,解得,
所以椭圆的方程为:.
证明:由题:过点的直线交椭圆于,两点,设直线,的斜率分别为,,
当直线的斜率存在时,设其方程为,,,,
由消去得:,
,解得或,
,,
因此,
当直线斜率不存在时,由,得,
不妨令,则,
所以与的和为定值.
21.解:因为,,
所以,.
所以,
则,
令,
则,
当时,恒成立,则单调递增,
又,所以恒成立,
则在上恒成立,
所以在上单调递增;
证明:令,其中,,
可得,
由可知在上单调递增,且,,
有,即恒成立,
即在上单调递增,
则,
即对任意,恒成立.
22.解:Ⅰ当时,如下表填数:
同行或同列的每一对数,计算较大数与较小数的比值分别为
,,,,可得此填数法的“特征值”为;
Ⅱ当时,如下表填数:
同行或同列的每一对数,计算较大数与较小数的比值分别为
,,,,,,,,,,,,,,,,,,
可得此填数法的“特征值”为;
Ⅲ不妨设为任意一个填数法,记此填数法的“特征值”为,
考虑含个元素的集合,
易知其中必有至少两个数处于同一行,设为
也必有至少两个数处于同一列,设为.
若
则有因为
若,即,
则,.
所以.
即不论何种情况,总有.
第1页,共1页
同课章节目录
