6.3 特殊平行四边形-矩形 同步练习(无答案)
文档属性
| 名称 | 6.3 特殊平行四边形-矩形 同步练习(无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 22.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-05-27 15:26:28 | ||
图片预览

文档简介
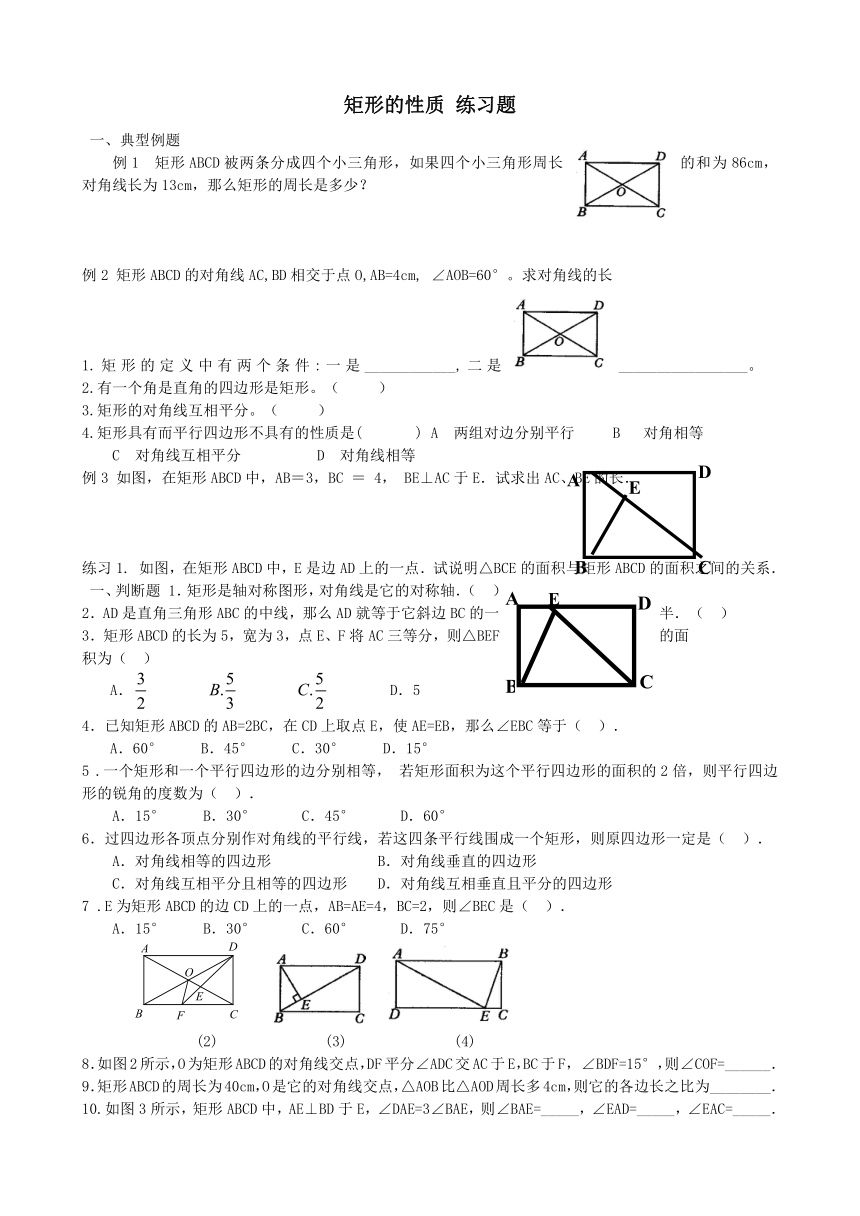
矩形的性质 练习题
一、典型例题
例1 矩形ABCD被两条分成四个小三角形,如果四个小三角形周长的和为86cm,对角线长为13cm,那么矩形的周长是多少?
例2 矩形ABCD的对角线AC,BD相交于点O,AB=4cm, ∠AOB=60°。求对角线的长
1.矩形的定义中有两个条件:一是____________,二是_________________。
2.有一个角是直角的四边形是矩形。( )
3.矩形的对角线互相平分。( )
4.矩形具有而平行四边形不具有的性质是( ) A 两组对边分别平行 B 对角相等
C 对角线互相平分 D 对角线相等
例3 如图,在矩形ABCD中,AB=3,BC = 4, BE⊥AC于E.试求出AC、BE的长.
练习1. 如图,在矩形ABCD中,E是边AD上的一点.试说明△BCE的面积与矩形ABCD的面积之间的关系.
一、判断题 1.矩形是轴对称图形,对角线是它的对称轴.( )
2.AD是直角三角形ABC的中线,那么AD就等于它斜边BC的一半.( )
3.矩形ABCD的长为5,宽为3,点E、F将AC三等分,则△BEF的面
积为( )
A. D.5
4.已知矩形ABCD的AB=2BC,在CD上取点E,使AE=EB,那么∠EBC等于( ).
A.60° B.45° C.30° D.15°
5 .一个矩形和一个平行四边形的边分别相等,若矩形面积为这个平行四边形的面积的2倍,则平行四边形的锐角的度数为( ).
A.15° B.30° C.45° D.60°
6.过四边形各顶点分别作对角线的平行线,若这四条平行线围成一个矩形,则原四边形一定是( ).
A.对角线相等的四边形 B.对角线垂直的四边形
C.对角线互相平分且相等的四边形 D.对角线互相垂直且平分的四边形
7 .E为矩形ABCD的边CD上的一点,AB=AE=4,BC=2,则∠BEC是( ).
A.15° B.30° C.60° D.75°
(2) (3) (4)
8.如图2所示,O为矩形ABCD的对角线交点,DF平分∠ADC交AC于E,BC于F,∠BDF=15°,则∠COF=______.
9.矩形ABCD的周长为40cm,O是它的对角线交点,△AOB比△AOD周长多4cm,则它的各边长之比为________.
10.如图3所示,矩形ABCD中,AE⊥BD于E,∠DAE=3∠BAE,则∠BAE=_____,∠EAD=_____,∠EAC=_____.
11.O为矩形ABCD的对角线交点,∠AOB=2∠BOC,对角线AC=12,则CB=_______.
12.如图4所示,在矩形ABCD中,AB=2BC,在CD上取点E,使AE=AB,则∠EAB=_____,∠BEC=________.
13、如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,E是AC的中点.若DE=5,则AB的长为 .
四、解答题
14.如图所示,矩形ABCD中,对角线AC、BD交于O点,CE⊥BD于E,OF⊥AB于F,BE:DE=1:3,OF=2cm,求AC的长.
D
E
A
C
B
E
A
B
D
C
一、典型例题
例1 矩形ABCD被两条分成四个小三角形,如果四个小三角形周长的和为86cm,对角线长为13cm,那么矩形的周长是多少?
例2 矩形ABCD的对角线AC,BD相交于点O,AB=4cm, ∠AOB=60°。求对角线的长
1.矩形的定义中有两个条件:一是____________,二是_________________。
2.有一个角是直角的四边形是矩形。( )
3.矩形的对角线互相平分。( )
4.矩形具有而平行四边形不具有的性质是( ) A 两组对边分别平行 B 对角相等
C 对角线互相平分 D 对角线相等
例3 如图,在矩形ABCD中,AB=3,BC = 4, BE⊥AC于E.试求出AC、BE的长.
练习1. 如图,在矩形ABCD中,E是边AD上的一点.试说明△BCE的面积与矩形ABCD的面积之间的关系.
一、判断题 1.矩形是轴对称图形,对角线是它的对称轴.( )
2.AD是直角三角形ABC的中线,那么AD就等于它斜边BC的一半.( )
3.矩形ABCD的长为5,宽为3,点E、F将AC三等分,则△BEF的面
积为( )
A. D.5
4.已知矩形ABCD的AB=2BC,在CD上取点E,使AE=EB,那么∠EBC等于( ).
A.60° B.45° C.30° D.15°
5 .一个矩形和一个平行四边形的边分别相等,若矩形面积为这个平行四边形的面积的2倍,则平行四边形的锐角的度数为( ).
A.15° B.30° C.45° D.60°
6.过四边形各顶点分别作对角线的平行线,若这四条平行线围成一个矩形,则原四边形一定是( ).
A.对角线相等的四边形 B.对角线垂直的四边形
C.对角线互相平分且相等的四边形 D.对角线互相垂直且平分的四边形
7 .E为矩形ABCD的边CD上的一点,AB=AE=4,BC=2,则∠BEC是( ).
A.15° B.30° C.60° D.75°
(2) (3) (4)
8.如图2所示,O为矩形ABCD的对角线交点,DF平分∠ADC交AC于E,BC于F,∠BDF=15°,则∠COF=______.
9.矩形ABCD的周长为40cm,O是它的对角线交点,△AOB比△AOD周长多4cm,则它的各边长之比为________.
10.如图3所示,矩形ABCD中,AE⊥BD于E,∠DAE=3∠BAE,则∠BAE=_____,∠EAD=_____,∠EAC=_____.
11.O为矩形ABCD的对角线交点,∠AOB=2∠BOC,对角线AC=12,则CB=_______.
12.如图4所示,在矩形ABCD中,AB=2BC,在CD上取点E,使AE=AB,则∠EAB=_____,∠BEC=________.
13、如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,E是AC的中点.若DE=5,则AB的长为 .
四、解答题
14.如图所示,矩形ABCD中,对角线AC、BD交于O点,CE⊥BD于E,OF⊥AB于F,BE:DE=1:3,OF=2cm,求AC的长.
D
E
A
C
B
E
A
B
D
C
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
