湖南省祁阳市浯溪二中2024-2025学年下学期中考一模数学仿真试卷(含答案)
文档属性
| 名称 | 湖南省祁阳市浯溪二中2024-2025学年下学期中考一模数学仿真试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 730.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-14 07:44:27 | ||
图片预览

文档简介
湖南省祁阳市浯溪二中2024-2025学年下学期中考一模数学仿真试卷
考试时间:120分钟 满分:120分
一.选择题(共10小题,每小题3分,满分30分)
1.﹣2025的相反数是( )
A.2025 B. C.﹣2025 D.
2.下列几何体中,俯视图与主视图形状相同的是( )
A.B.C. D.
3.下列计算正确的是( )
A.a6÷a2=a3 B.(﹣a2)5=﹣a7 C.(a+1)(1﹣a)=1﹣a2 D.(a+1)2=a2+1
4.截止2024年末,我市常住人口为434.3万人,其中434.3万用科学记数法表示为( )
A.43.43×105 B.4.343×106 C.4.343×107 D.0.4343×108
5.设点P(x,y)在第二象限内,且|x|=3,|y|=2,则点P关于原点的对称点为( )
A.(2,3) B.(﹣2,3) C.(3,﹣2) D.(﹣3,2)
6.如图,将一张含有30°角的三角形纸片的两个顶点分别叠放在长方形的两条对边上.若∠2=40°,则∠1的度数为( )
A.10° B.20° C.90°﹣α D.α﹣40°
7.如图,某同学用一个等边三角形ABC和一个正五边形BCDEF设计了一个宝石徽章,其中BC为两个图形的公共边,连接AE,CF交于点G,下列说法错误的是( )
A.AC⊥CF B.DE∥CF C.△EFG是等腰三角形 D.AE垂直平分BC
第6题图 第7题图 第8题图 第10题图
8.如图,BC是⊙O的直径,点A、D在⊙O上,若∠ADC=42°,则∠ACB等于( )
A.60° B.54° C.48° D.42°
9.已知一组数据:3,4,4,5,添加一个数据得到一组新的数据后,新的统计量(平均数、中位数、众数、方差)与原来相比有且只有一个发生变化,这个变化的统计量是( )
A.平均数 B.中位数 C.众数 D.方差
10.如图平面直角坐标系中,A(0,7)、,C为线段OA上一个动点.以CB为边作直角三角形BCD,∠BCD=90°且∠CBD=60°,连接AD,当AD有最小值时,点D的坐标为( )
A.(0,3) B. C. D.
二.填空题(共8小题,满分24分,每小题3分)
11.若二次根式有意义,则x的取值范围是 .
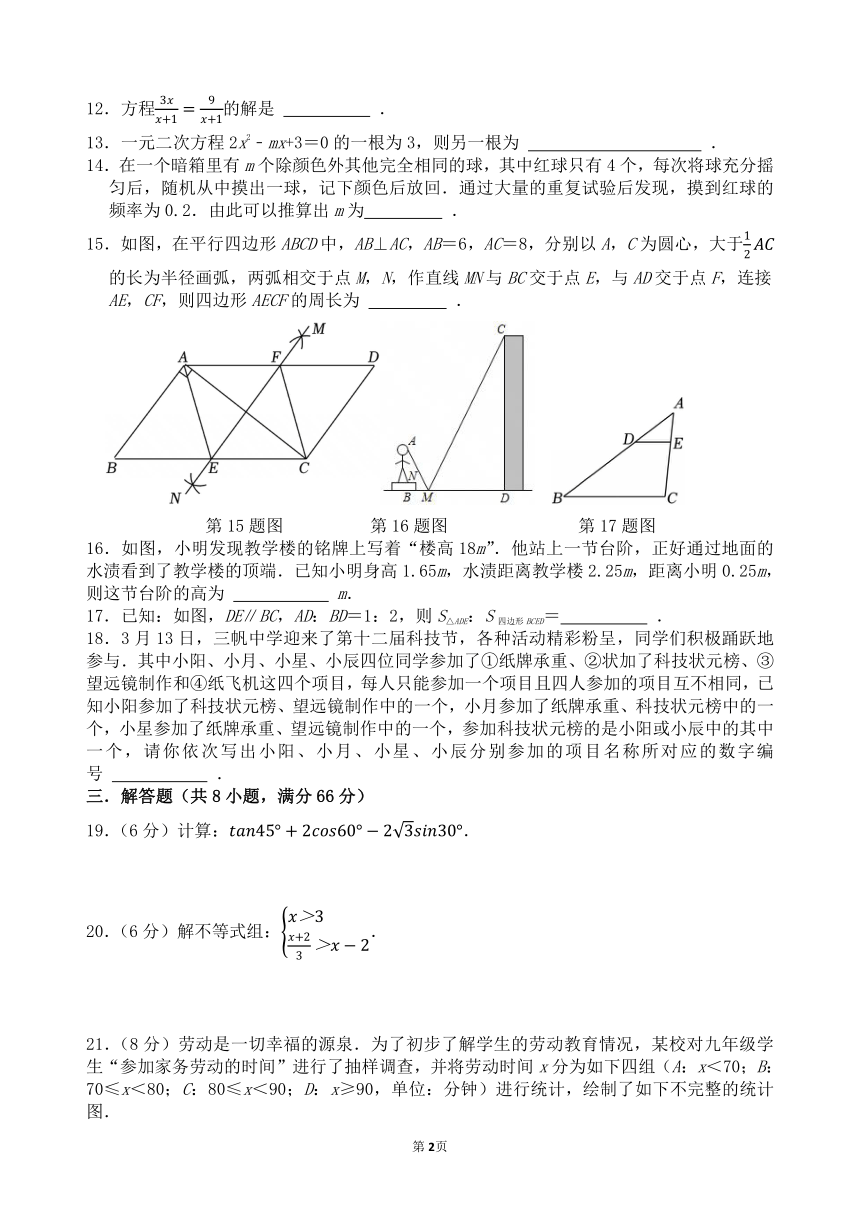
12.方程的解是 .
13.一元二次方程2x2﹣mx+3=0的一根为3,则另一根为 .
14.在一个暗箱里有m个除颜色外其他完全相同的球,其中红球只有4个,每次将球充分摇匀后,随机从中摸出一球,记下颜色后放回.通过大量的重复试验后发现,摸到红球的频率为0.2.由此可以推算出m为 .
15.如图,在平行四边形ABCD中,AB⊥AC,AB=6,AC=8,分别以A,C为圆心,大于的长为半径画弧,两弧相交于点M,N,作直线MN与BC交于点E,与AD交于点F,连接AE,CF,则四边形AECF的周长为 .
第15题图 第16题图 第17题图
16.如图,小明发现教学楼的铭牌上写着“楼高18m”.他站上一节台阶,正好通过地面的水渍看到了教学楼的顶端.已知小明身高1.65m,水渍距离教学楼2.25m,距离小明0.25m,则这节台阶的高为 m.
17.已知:如图,DE∥BC,AD:BD=1:2,则S△ADE:S四边形BCED= .
18.3月13日,三帆中学迎来了第十二届科技节,各种活动精彩粉呈,同学们积极踊跃地参与.其中小阳、小月、小星、小辰四位同学参加了①纸牌承重、②状加了科技状元榜、③望远镜制作和④纸飞机这四个项目,每人只能参加一个项目且四人参加的项目互不相同,已知小阳参加了科技状元榜、望远镜制作中的一个,小月参加了纸牌承重、科技状元榜中的一个,小星参加了纸牌承重、望远镜制作中的一个,参加科技状元榜的是小阳或小辰中的其中一个,请你依次写出小阳、小月、小星、小辰分别参加的项目名称所对应的数字编号 .
三.解答题(共8小题,满分66分)
19.(6分)计算:.
20.(6分)解不等式组:.
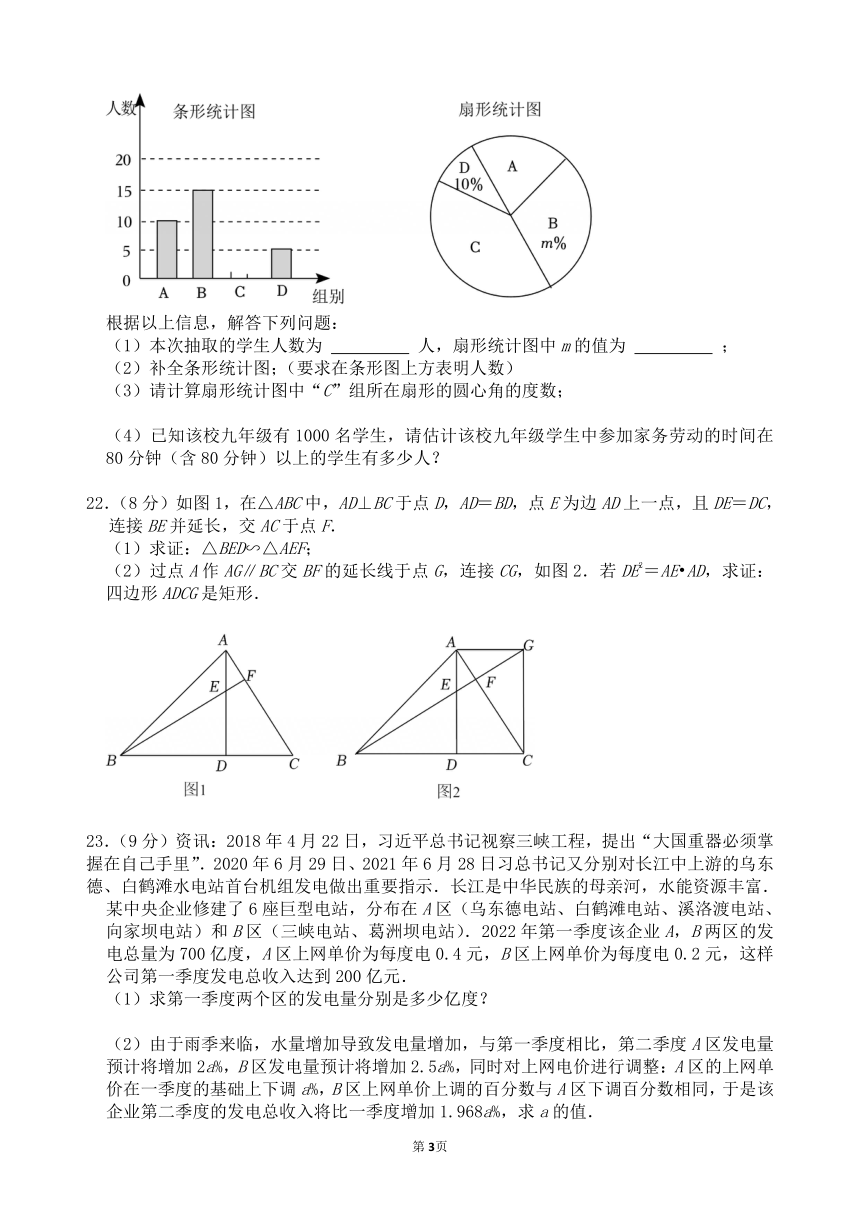
21.(8分)劳动是一切幸福的源泉.为了初步了解学生的劳动教育情况,某校对九年级学生“参加家务劳动的时间”进行了抽样调查,并将劳动时间x分为如下四组(A:x<70;B:70≤x<80;C:80≤x<90;D:x≥90,单位:分钟)进行统计,绘制了如下不完整的统计图.
根据以上信息,解答下列问题:
(1)本次抽取的学生人数为 人,扇形统计图中m的值为 ;
(2)补全条形统计图;(要求在条形图上方表明人数)
(3)请计算扇形统计图中“C”组所在扇形的圆心角的度数;
(4)已知该校九年级有1000名学生,请估计该校九年级学生中参加家务劳动的时间在80分钟(含80分钟)以上的学生有多少人?
22.(8分)如图1,在△ABC中,AD⊥BC于点D,AD=BD,点E为边AD上一点,且DE=DC,连接BE并延长,交AC于点F.
(1)求证:△BED∽△AEF;
(2)过点A作AG∥BC交BF的延长线于点G,连接CG,如图2.若DE2=AE AD,求证:四边形ADCG是矩形.
23.(9分)资讯:2018年4月22日,习近平总书记视察三峡工程,提出“大国重器必须掌握在自己手里”.2020年6月29日、2021年6月28日习总书记又分别对长江中上游的乌东德、白鹤滩水电站首台机组发电做出重要指示.长江是中华民族的母亲河,水能资源丰富.
某中央企业修建了6座巨型电站,分布在A区(乌东德电站、白鹤滩电站、溪洛渡电站、向家坝电站)和B区(三峡电站、葛洲坝电站).2022年第一季度该企业A,B两区的发电总量为700亿度,A区上网单价为每度电0.4元,B区上网单价为每度电0.2元,这样公司第一季度发电总收入达到200亿元.
(1)求第一季度两个区的发电量分别是多少亿度?
(2)由于雨季来临,水量增加导致发电量增加,与第一季度相比,第二季度A区发电量预计将增加2a%,B区发电量预计将增加2.5a%,同时对上网电价进行调整:A区的上网单价在一季度的基础上下调a%,B区上网单价上调的百分数与A区下调百分数相同,于是该企业第二季度的发电总收入将比一季度增加1.968a%,求a的值.
24.(9分)某房地产集团筹建一小区,居民楼均为平顶条式,南北朝向,楼高统一为16m(五层).已知该城市冬至正午时分太阳高度最低,太阳光线与水平线的夹角为32°.
(1)如果甲、乙两楼相隔仅有20m(如图),试求此时甲楼的影子落在乙楼上有多高;
(2)根据居住要求,每层楼在冬天都要受到阳光照射,请你重新设计一个方案.(精确到0.1m,参考数据:tan32°≈0.6249)
25.(10分)如图,直线y=﹣x+3与x轴的正半轴、y轴的正半轴分别相交于点A和点C,点B是点A关于原点O的对称点,四边形ABCD是平行四边形,抛物线y=ax2+bx﹣10经过点B和点D.
(1)求平行四边形ABCD的面积;
(2)求抛物线的解析式;
(3)动点P从点C出发,以每秒1个单位的速度匀速运动到点D;同时动点Q从点A出发,以每秒1个单位的速度匀速运动到点C,设运动的时间为t.
①当CP=CQ时,求t的值;
②请你猜想,在P,Q两点的运动过程中,是否存在某一时刻t,使得四边形ADPQ的面积最小?若存在,求出t的值,并求出这个最小值;若不存在,请说明理由.
26.(10分)如图,直线y=﹣x+b与x轴交于点A,与y轴交于点B,过原点O,点A和点B三点作⊙P,再过点A作⊙P的切线AM,Q为AM上一动点,过点Q作y轴的垂线,交y轴于点C,连接BQ,交⊙P于点D.
(1)求∠CQA的度数;
(2)连接DO,AD,当时,△DOA恰好为等腰三角形,求此时b的值;
(3)连接PC,DC,PC交BQ于点F,PC∥AD时,记△PFB的面积为S1,△CDF的面积为S2,求.
参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A C C B. C A A C D C
11.x.12.x=3.13..14.20. 15. 20.16. 0.35.17. 1:8.18.②①③④.
19.解:原式=1+2=1+1.
20.解:,由①得:x>3,由②得:x<4,∴不等式组的解集为3<x<4.
21.解:(1)本次抽取的学生人数为:5÷10%=50(人);,故答案为:50,30;(2)C组人数为:50﹣(10+15+5)=20(人),
如图:(3);(4)∵(人),∴时间在80分钟(含80分钟)以上的学生有500人.
22.证明:(1)如图1,
∵AD⊥BC,∴∠ADC=∠BDE=90°,∵AD=BD,DC=DE,∴△ACD≌△BED(SAS),
∴∠EBD=∠CAD,∵∠BED=∠AEF,∴△BED∽△AEF;(2)如图2,∵AG∥BC,∴∠AGE=∠EDB,∵∠EBD=∠CAD,∴∠AGE=∠CAD,∵∠AEG=∠BED=∠ACD,∴△AEG∽△DCA,
∴,∴AE AD=DC AG,∵DE2=AE AD,∴DC AG=DE2,∵DE=DC,∴DC AG=DC2,∴DC=AG,∵AG∥DC,∴四边形ADCG是平行四边形,∵AD⊥BC,∴四边形ADCG是矩形.
23.解:(1)设第一季度A区的发电量是x亿度,B区的发电量是y亿度,
依题意得:,解得:.
答:第一季度A区的发电量是300亿度,B区的发电量是400亿度.
(2)依题意得:0.4(1﹣a%)×300(1+2a%)+0.2(1+a%)×400(1+2.5a%)=200(1+1.968a%),
整理得:0.004a2﹣0.064a=0,解得:a1=16,a2=0(不合题意,舍去).
答:a的值为16.
24.解:(1)如图,过点C作CE⊥AB于E,由题意可知∠ACE=32°,CE=BD=20m.
在Rt△ACE中,∵tan∠ACE,∴AE=CE tan∠ACE=20 tan32°≈12.5,
∴DC=EB=AB﹣AE=16﹣12.5=3.5.答:此时南楼的影子落在北楼上约3.5米高;
(2)如图,设射线AC交直线BD于点F.在Rt△ABF中,∵AB=16,∠F=32°,
∴BF25.6.答:如按城市规划要求,使前后楼每层居民在冬天都能有阳光,两楼间的距离约是25.6米.
25.解:(1)当x=0时,y=3,∴C(0,3),当y=0时,x=3,∴A(3,0),∵点B是点A关于原点O的对称点,∴B(﹣3,0),∴AB=6,∴平行四边形ABCD的面积=AB CO=6×3=18;
(2)∵四边形ABCD是平行四边形,AB=6,∴D(6,3),将B点、D点代入y=ax2+bx﹣10,∴,解得,∴抛物线的解析式为yx2x﹣10;
(3)①∵A(3,0),C(0,3),∴AC=3,∵CP=CQ,∴t=3t,解得t;
②存在t,使得四边形ABCD的面积最小,理由如下:
当t=3时,点Q、CC重合,此时四边形ADPQ为三角形,且面积不为最小值,
故只研究0≤t≤3运动的情况,t秒时,点Q的纵坐标为t,
则四边形ADPQ的面积=S△ADC﹣S△CPQCD×OCCP×(yC﹣yQ)
t×(3t)t2t+9(t)2,
即t时,四边形ADPQ的面积的最小值为:.
26.解:(1)由题意得,OA=OB=b,∠AOB=90°,∴∠OAB=∠OBA=45°,∵AQ是⊙P的切线,∴∠BAQ=90°,∴∠OAQ=∠OAB+∠BAQ=135°,∵QC⊥y轴,OA⊥OB,∴CQ∥OA,
∴∠CQA=180°﹣∠OAQ=45°;(2)如图1,
当OD=AD时,
连接OP,PD,在AQ上截取AE=AB,连接BE,
∴OP=AP,PD=PD,∴△ADP≌△ODP(SSS),∴∠ADP=∠ODP,∴DP⊥OA,∵OB⊥OA,
∵OB∥DP,∴∠DPB=∠OBA=45°,∵PD=PA,
∴∠PAD=∠ADP,
∵AB是⊙P的直径,
∴∠ADB=90°,
∴∠ABD=90°﹣∠BAD=67.5°,
∵∠BAQ=90°,AB=AE,
∴∠Q=90°﹣∠ABD=22.5°,∠AEB=∠ABE=45°,
∴∠QEB=∠AEB﹣∠Q=22.5°,BEAB,
∴∠Q=∠EBQ,
∴BE=EQAE,∵AQ=2,∴AB=4﹣2,∵,∴b=2,
如图2,
当OA=OD时,∵∠ADB=90°,AD=OAAB,∴∠BAD=∠ABD=45°,
∵∠BAQ=90°,∴△ABD是等腰直角三角形,∴AB=AQ=2,
∴b,综上所述:b=2或2;
(3)如图3,作PG⊥OC于G,∵PC∥AD,AD⊥BD,
∴PC⊥BD,设Q(a+b,a),则C(0,a),∵B(0,b),
∴BC=a﹣b,∵∠BCQ=90°,
∴∠BQC+∠CBQ=90°,
∵∠CFB=90°,
∴∠BCF+∠CBQ=90°,
∴∠BCF=∠CQB,
∴tan∠BCF=tan∠CQB,
∴,
∴,∴a=2b,
∴tan∠CBF,
∵AB,AQa=2,
∴tan∠BPF=tan∠AQB,∵PF⊥BD,∴BF=DF,
∴S△BCF=S△CDF,
∵tan∠BCF,tan∠BPF,
∴,∴,∴.
第5页
考试时间:120分钟 满分:120分
一.选择题(共10小题,每小题3分,满分30分)
1.﹣2025的相反数是( )
A.2025 B. C.﹣2025 D.
2.下列几何体中,俯视图与主视图形状相同的是( )
A.B.C. D.
3.下列计算正确的是( )
A.a6÷a2=a3 B.(﹣a2)5=﹣a7 C.(a+1)(1﹣a)=1﹣a2 D.(a+1)2=a2+1
4.截止2024年末,我市常住人口为434.3万人,其中434.3万用科学记数法表示为( )
A.43.43×105 B.4.343×106 C.4.343×107 D.0.4343×108
5.设点P(x,y)在第二象限内,且|x|=3,|y|=2,则点P关于原点的对称点为( )
A.(2,3) B.(﹣2,3) C.(3,﹣2) D.(﹣3,2)
6.如图,将一张含有30°角的三角形纸片的两个顶点分别叠放在长方形的两条对边上.若∠2=40°,则∠1的度数为( )
A.10° B.20° C.90°﹣α D.α﹣40°
7.如图,某同学用一个等边三角形ABC和一个正五边形BCDEF设计了一个宝石徽章,其中BC为两个图形的公共边,连接AE,CF交于点G,下列说法错误的是( )
A.AC⊥CF B.DE∥CF C.△EFG是等腰三角形 D.AE垂直平分BC
第6题图 第7题图 第8题图 第10题图
8.如图,BC是⊙O的直径,点A、D在⊙O上,若∠ADC=42°,则∠ACB等于( )
A.60° B.54° C.48° D.42°
9.已知一组数据:3,4,4,5,添加一个数据得到一组新的数据后,新的统计量(平均数、中位数、众数、方差)与原来相比有且只有一个发生变化,这个变化的统计量是( )
A.平均数 B.中位数 C.众数 D.方差
10.如图平面直角坐标系中,A(0,7)、,C为线段OA上一个动点.以CB为边作直角三角形BCD,∠BCD=90°且∠CBD=60°,连接AD,当AD有最小值时,点D的坐标为( )
A.(0,3) B. C. D.
二.填空题(共8小题,满分24分,每小题3分)
11.若二次根式有意义,则x的取值范围是 .
12.方程的解是 .
13.一元二次方程2x2﹣mx+3=0的一根为3,则另一根为 .
14.在一个暗箱里有m个除颜色外其他完全相同的球,其中红球只有4个,每次将球充分摇匀后,随机从中摸出一球,记下颜色后放回.通过大量的重复试验后发现,摸到红球的频率为0.2.由此可以推算出m为 .
15.如图,在平行四边形ABCD中,AB⊥AC,AB=6,AC=8,分别以A,C为圆心,大于的长为半径画弧,两弧相交于点M,N,作直线MN与BC交于点E,与AD交于点F,连接AE,CF,则四边形AECF的周长为 .
第15题图 第16题图 第17题图
16.如图,小明发现教学楼的铭牌上写着“楼高18m”.他站上一节台阶,正好通过地面的水渍看到了教学楼的顶端.已知小明身高1.65m,水渍距离教学楼2.25m,距离小明0.25m,则这节台阶的高为 m.
17.已知:如图,DE∥BC,AD:BD=1:2,则S△ADE:S四边形BCED= .
18.3月13日,三帆中学迎来了第十二届科技节,各种活动精彩粉呈,同学们积极踊跃地参与.其中小阳、小月、小星、小辰四位同学参加了①纸牌承重、②状加了科技状元榜、③望远镜制作和④纸飞机这四个项目,每人只能参加一个项目且四人参加的项目互不相同,已知小阳参加了科技状元榜、望远镜制作中的一个,小月参加了纸牌承重、科技状元榜中的一个,小星参加了纸牌承重、望远镜制作中的一个,参加科技状元榜的是小阳或小辰中的其中一个,请你依次写出小阳、小月、小星、小辰分别参加的项目名称所对应的数字编号 .
三.解答题(共8小题,满分66分)
19.(6分)计算:.
20.(6分)解不等式组:.
21.(8分)劳动是一切幸福的源泉.为了初步了解学生的劳动教育情况,某校对九年级学生“参加家务劳动的时间”进行了抽样调查,并将劳动时间x分为如下四组(A:x<70;B:70≤x<80;C:80≤x<90;D:x≥90,单位:分钟)进行统计,绘制了如下不完整的统计图.
根据以上信息,解答下列问题:
(1)本次抽取的学生人数为 人,扇形统计图中m的值为 ;
(2)补全条形统计图;(要求在条形图上方表明人数)
(3)请计算扇形统计图中“C”组所在扇形的圆心角的度数;
(4)已知该校九年级有1000名学生,请估计该校九年级学生中参加家务劳动的时间在80分钟(含80分钟)以上的学生有多少人?
22.(8分)如图1,在△ABC中,AD⊥BC于点D,AD=BD,点E为边AD上一点,且DE=DC,连接BE并延长,交AC于点F.
(1)求证:△BED∽△AEF;
(2)过点A作AG∥BC交BF的延长线于点G,连接CG,如图2.若DE2=AE AD,求证:四边形ADCG是矩形.
23.(9分)资讯:2018年4月22日,习近平总书记视察三峡工程,提出“大国重器必须掌握在自己手里”.2020年6月29日、2021年6月28日习总书记又分别对长江中上游的乌东德、白鹤滩水电站首台机组发电做出重要指示.长江是中华民族的母亲河,水能资源丰富.
某中央企业修建了6座巨型电站,分布在A区(乌东德电站、白鹤滩电站、溪洛渡电站、向家坝电站)和B区(三峡电站、葛洲坝电站).2022年第一季度该企业A,B两区的发电总量为700亿度,A区上网单价为每度电0.4元,B区上网单价为每度电0.2元,这样公司第一季度发电总收入达到200亿元.
(1)求第一季度两个区的发电量分别是多少亿度?
(2)由于雨季来临,水量增加导致发电量增加,与第一季度相比,第二季度A区发电量预计将增加2a%,B区发电量预计将增加2.5a%,同时对上网电价进行调整:A区的上网单价在一季度的基础上下调a%,B区上网单价上调的百分数与A区下调百分数相同,于是该企业第二季度的发电总收入将比一季度增加1.968a%,求a的值.
24.(9分)某房地产集团筹建一小区,居民楼均为平顶条式,南北朝向,楼高统一为16m(五层).已知该城市冬至正午时分太阳高度最低,太阳光线与水平线的夹角为32°.
(1)如果甲、乙两楼相隔仅有20m(如图),试求此时甲楼的影子落在乙楼上有多高;
(2)根据居住要求,每层楼在冬天都要受到阳光照射,请你重新设计一个方案.(精确到0.1m,参考数据:tan32°≈0.6249)
25.(10分)如图,直线y=﹣x+3与x轴的正半轴、y轴的正半轴分别相交于点A和点C,点B是点A关于原点O的对称点,四边形ABCD是平行四边形,抛物线y=ax2+bx﹣10经过点B和点D.
(1)求平行四边形ABCD的面积;
(2)求抛物线的解析式;
(3)动点P从点C出发,以每秒1个单位的速度匀速运动到点D;同时动点Q从点A出发,以每秒1个单位的速度匀速运动到点C,设运动的时间为t.
①当CP=CQ时,求t的值;
②请你猜想,在P,Q两点的运动过程中,是否存在某一时刻t,使得四边形ADPQ的面积最小?若存在,求出t的值,并求出这个最小值;若不存在,请说明理由.
26.(10分)如图,直线y=﹣x+b与x轴交于点A,与y轴交于点B,过原点O,点A和点B三点作⊙P,再过点A作⊙P的切线AM,Q为AM上一动点,过点Q作y轴的垂线,交y轴于点C,连接BQ,交⊙P于点D.
(1)求∠CQA的度数;
(2)连接DO,AD,当时,△DOA恰好为等腰三角形,求此时b的值;
(3)连接PC,DC,PC交BQ于点F,PC∥AD时,记△PFB的面积为S1,△CDF的面积为S2,求.
参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A C C B. C A A C D C
11.x.12.x=3.13..14.20. 15. 20.16. 0.35.17. 1:8.18.②①③④.
19.解:原式=1+2=1+1.
20.解:,由①得:x>3,由②得:x<4,∴不等式组的解集为3<x<4.
21.解:(1)本次抽取的学生人数为:5÷10%=50(人);,故答案为:50,30;(2)C组人数为:50﹣(10+15+5)=20(人),
如图:(3);(4)∵(人),∴时间在80分钟(含80分钟)以上的学生有500人.
22.证明:(1)如图1,
∵AD⊥BC,∴∠ADC=∠BDE=90°,∵AD=BD,DC=DE,∴△ACD≌△BED(SAS),
∴∠EBD=∠CAD,∵∠BED=∠AEF,∴△BED∽△AEF;(2)如图2,∵AG∥BC,∴∠AGE=∠EDB,∵∠EBD=∠CAD,∴∠AGE=∠CAD,∵∠AEG=∠BED=∠ACD,∴△AEG∽△DCA,
∴,∴AE AD=DC AG,∵DE2=AE AD,∴DC AG=DE2,∵DE=DC,∴DC AG=DC2,∴DC=AG,∵AG∥DC,∴四边形ADCG是平行四边形,∵AD⊥BC,∴四边形ADCG是矩形.
23.解:(1)设第一季度A区的发电量是x亿度,B区的发电量是y亿度,
依题意得:,解得:.
答:第一季度A区的发电量是300亿度,B区的发电量是400亿度.
(2)依题意得:0.4(1﹣a%)×300(1+2a%)+0.2(1+a%)×400(1+2.5a%)=200(1+1.968a%),
整理得:0.004a2﹣0.064a=0,解得:a1=16,a2=0(不合题意,舍去).
答:a的值为16.
24.解:(1)如图,过点C作CE⊥AB于E,由题意可知∠ACE=32°,CE=BD=20m.
在Rt△ACE中,∵tan∠ACE,∴AE=CE tan∠ACE=20 tan32°≈12.5,
∴DC=EB=AB﹣AE=16﹣12.5=3.5.答:此时南楼的影子落在北楼上约3.5米高;
(2)如图,设射线AC交直线BD于点F.在Rt△ABF中,∵AB=16,∠F=32°,
∴BF25.6.答:如按城市规划要求,使前后楼每层居民在冬天都能有阳光,两楼间的距离约是25.6米.
25.解:(1)当x=0时,y=3,∴C(0,3),当y=0时,x=3,∴A(3,0),∵点B是点A关于原点O的对称点,∴B(﹣3,0),∴AB=6,∴平行四边形ABCD的面积=AB CO=6×3=18;
(2)∵四边形ABCD是平行四边形,AB=6,∴D(6,3),将B点、D点代入y=ax2+bx﹣10,∴,解得,∴抛物线的解析式为yx2x﹣10;
(3)①∵A(3,0),C(0,3),∴AC=3,∵CP=CQ,∴t=3t,解得t;
②存在t,使得四边形ABCD的面积最小,理由如下:
当t=3时,点Q、CC重合,此时四边形ADPQ为三角形,且面积不为最小值,
故只研究0≤t≤3运动的情况,t秒时,点Q的纵坐标为t,
则四边形ADPQ的面积=S△ADC﹣S△CPQCD×OCCP×(yC﹣yQ)
t×(3t)t2t+9(t)2,
即t时,四边形ADPQ的面积的最小值为:.
26.解:(1)由题意得,OA=OB=b,∠AOB=90°,∴∠OAB=∠OBA=45°,∵AQ是⊙P的切线,∴∠BAQ=90°,∴∠OAQ=∠OAB+∠BAQ=135°,∵QC⊥y轴,OA⊥OB,∴CQ∥OA,
∴∠CQA=180°﹣∠OAQ=45°;(2)如图1,
当OD=AD时,
连接OP,PD,在AQ上截取AE=AB,连接BE,
∴OP=AP,PD=PD,∴△ADP≌△ODP(SSS),∴∠ADP=∠ODP,∴DP⊥OA,∵OB⊥OA,
∵OB∥DP,∴∠DPB=∠OBA=45°,∵PD=PA,
∴∠PAD=∠ADP,
∵AB是⊙P的直径,
∴∠ADB=90°,
∴∠ABD=90°﹣∠BAD=67.5°,
∵∠BAQ=90°,AB=AE,
∴∠Q=90°﹣∠ABD=22.5°,∠AEB=∠ABE=45°,
∴∠QEB=∠AEB﹣∠Q=22.5°,BEAB,
∴∠Q=∠EBQ,
∴BE=EQAE,∵AQ=2,∴AB=4﹣2,∵,∴b=2,
如图2,
当OA=OD时,∵∠ADB=90°,AD=OAAB,∴∠BAD=∠ABD=45°,
∵∠BAQ=90°,∴△ABD是等腰直角三角形,∴AB=AQ=2,
∴b,综上所述:b=2或2;
(3)如图3,作PG⊥OC于G,∵PC∥AD,AD⊥BD,
∴PC⊥BD,设Q(a+b,a),则C(0,a),∵B(0,b),
∴BC=a﹣b,∵∠BCQ=90°,
∴∠BQC+∠CBQ=90°,
∵∠CFB=90°,
∴∠BCF+∠CBQ=90°,
∴∠BCF=∠CQB,
∴tan∠BCF=tan∠CQB,
∴,
∴,∴a=2b,
∴tan∠CBF,
∵AB,AQa=2,
∴tan∠BPF=tan∠AQB,∵PF⊥BD,∴BF=DF,
∴S△BCF=S△CDF,
∵tan∠BCF,tan∠BPF,
∴,∴,∴.
第5页
同课章节目录
