26.2 圆的对称性--垂径定理
图片预览




文档简介
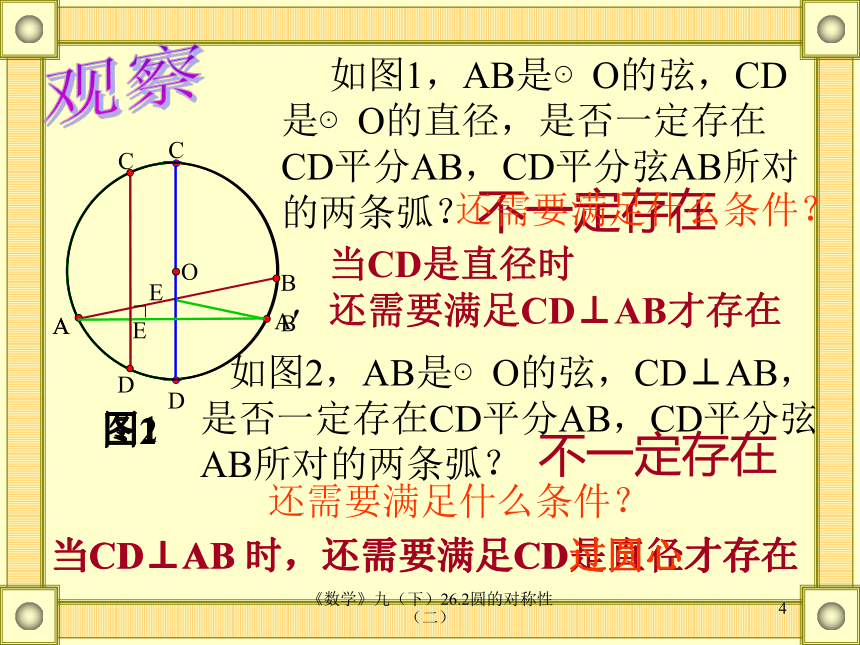
课件27张PPT。2009-12-15义务教育课程标准实验教科书《数学》九(下)126.2 圆的对称性第二课时 垂径定理桃铺中学 阮《数学》九(下)26.2圆的对称性(二)2复习提问1、什么是轴对称图形?我们初中学过的轴对称图形有哪些? 如果一个图形沿某条直线折叠后,直线两旁的部分能够完全重合,那么这个图形叫做轴对称图形。 矩形、正方形、等腰三角形、等边三角形、圆、扇形、等腰梯形、线段、角等等。2、圆是轴对称图形,它的对称轴是什么?你能找到多少条对称轴? 对称轴是任意一条过圆心的直线。无数条 你是用什么方法解决上述问题的?可利用折叠的方法。《数学》九(下)26.2圆的对称性(二)3探究 1、在纸上任意画一⊙O,对折,在半圆上用针刺一个小孔,得到两个重合的点A、BCDABEO直径再把对折的圆摊平,那么折痕CD是 ; 2、连接AB,这里直径CD与弦AB有怎样的位置关系? CD垂直平分AB即CD平分弦AB所对的两条弧《数学》九(下)26.2圆的对称性(二)4CEOBA′DAA观察 如图1,AB是⊙O的弦,CD是⊙O的直径,是否一定存在CD平分AB,CD平分弦AB所对的两条弧?当CD是直径时
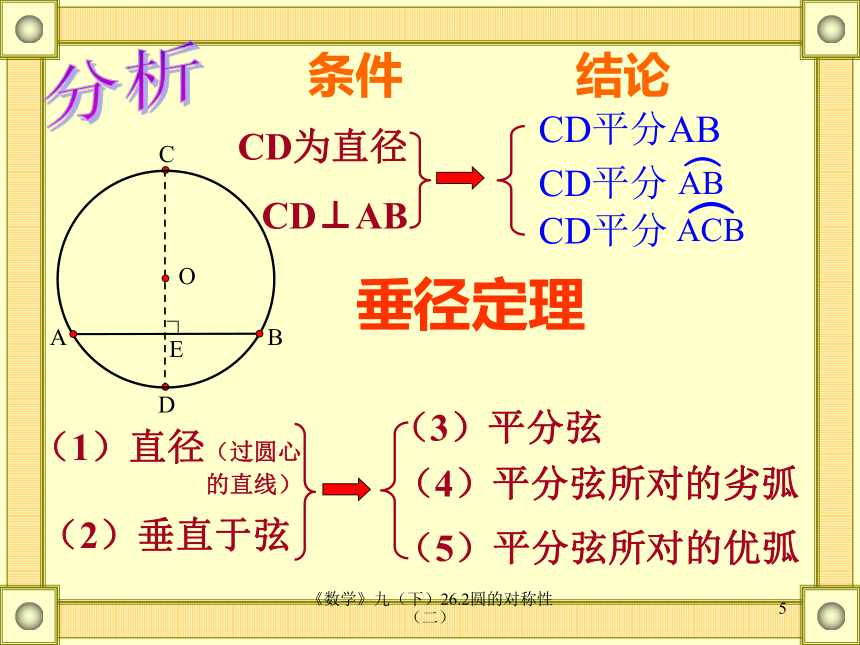
还需要满足CD⊥AB才存在 如图2,AB是⊙O的弦,CD⊥AB,是否一定存在CD平分AB,CD平分弦AB所对的两条弧?BCDE不一定存在还需要满足什么条件?不一定存在还需要满足什么条件?当CD⊥AB 时,还需要满足CD是直径才存在当CD⊥AB 时,还需要满足CD过圆心才存在图1图2《数学》九(下)26.2圆的对称性(二)5条件结论CD为直径
CD⊥ABO分析CD平分AB(1)直径(过圆心的直线)
(2)垂直于弦 (3)平分弦(4)平分弦所对的劣弧(5)平分弦所对的优弧垂径定理《数学》九(下)26.2圆的对称性(二)6归纳垂径定理 垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧。1、文字语言2、数学语言∵ CD是⊙O的直径
CD⊥AB
∴ AE = EB
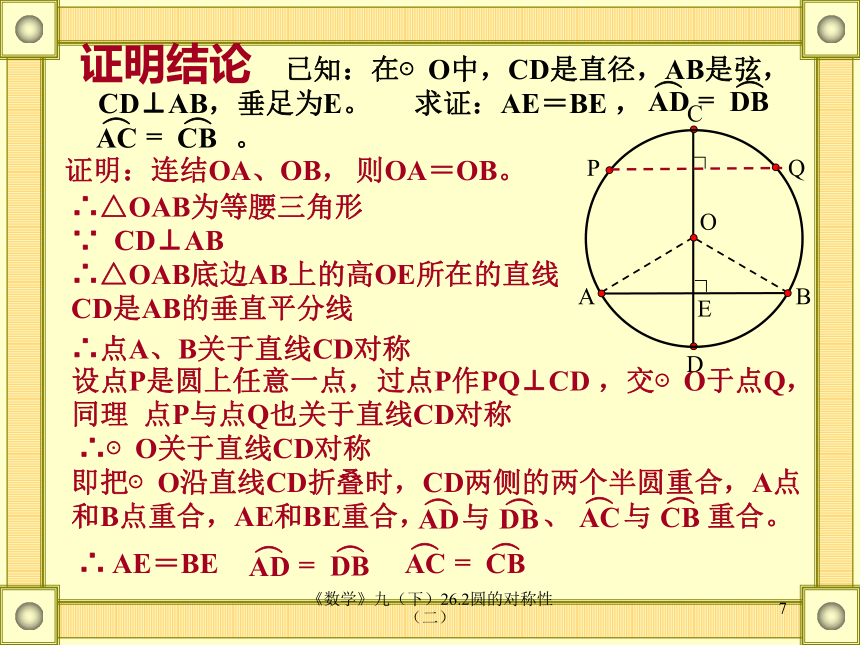
3、图形语言O《数学》九(下)26.2圆的对称性(二)7证明结论O证明:连结OA、OB,∴△OAB为等腰三角形∵ CD⊥AB∴△OAB底边AB上的高OE所在的直线CD是AB的垂直平分线∴点A、B关于直线CD对称则OA=OB。设点P是圆上任意一点,过点P作PQ⊥CD ,交⊙O于点Q,∴ AE=BE 已知:在⊙O中,CD是直径,AB是弦,CD⊥AB,垂足为E。 求证:AE=BE ,
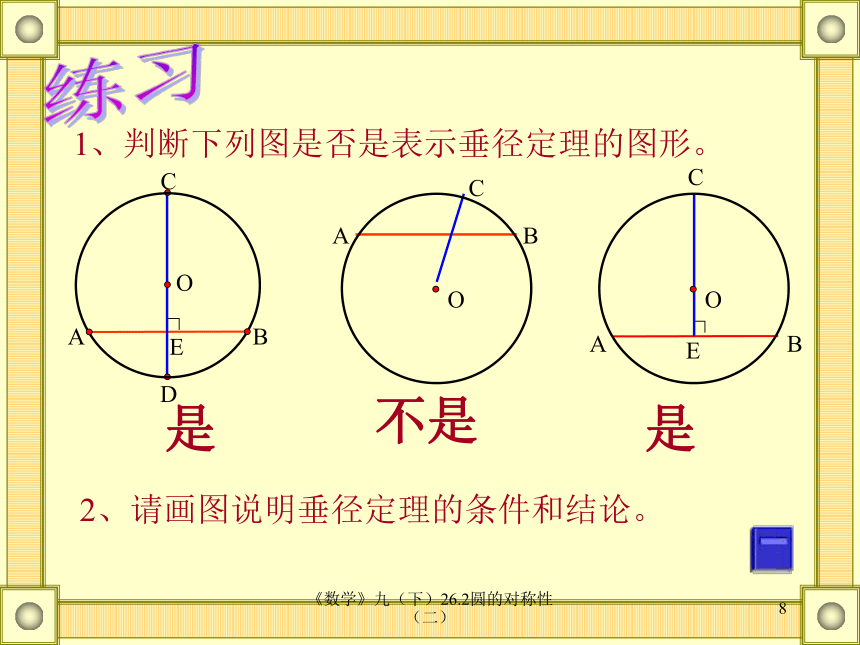
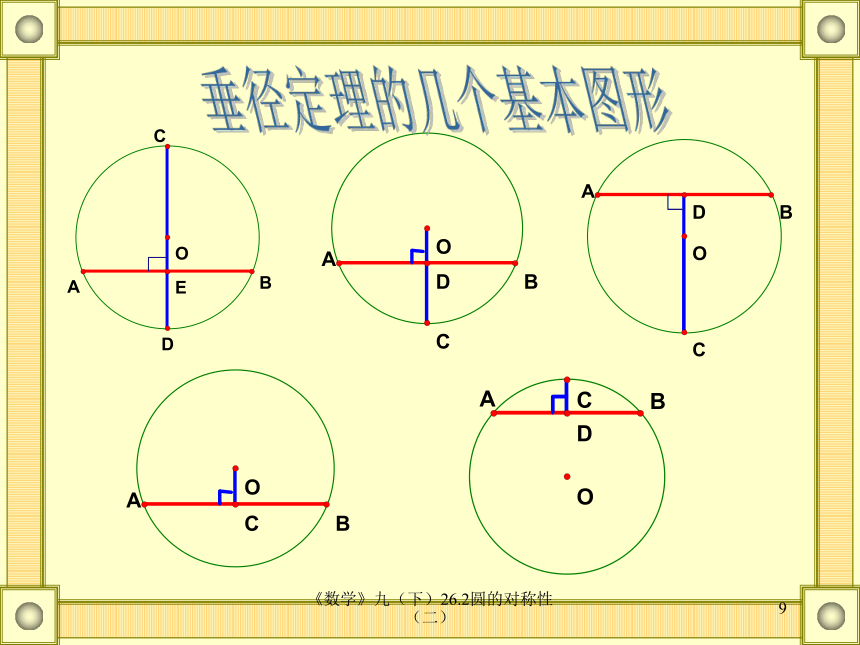
。∴⊙O关于直线CD对称P同理 点P与点Q也关于直线CD对称Q《数学》九(下)26.2圆的对称性(二)82、请画图说明垂径定理的条件和结论。1、判断下列图是否是表示垂径定理的图形。是不是是O练习《数学》九(下)26.2圆的对称性(二)9垂径定理的几个基本图形《数学》九(下)26.2圆的对称性(二)10例1 如图,已知在⊙O中,弦AB的长为8厘米,圆心O到AB的距离为3厘米,求⊙O的半径。解:连结OA。过O作OE⊥AB,垂足为E例题1《数学》九(下)26.2圆的对称性(二)11例题2 已知:如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C,D两点。
求证:AC=BD。ABCD证明:过O作OE⊥AB,垂足为E∴ AE=BE CE=DE ∴ AE-CE=BE-DE∴ AC=BD?《数学》九(下)26.2圆的对称性(二)12MN例题3证明:作直径MN⊥AB∵ AB∥CD∴ MN⊥CD∟∴(垂直于弦的直径平分弦所对的弧)∴推论:
圆的两条平行弦所夹的弧相等数学语言:∵AB∥CD ∴《数学》九(下)26.2圆的对称性(二)13O探究ECDAB∟由垂径定理可知:
① ② ③ ④ ⑤(1)① ③ ② ④ ⑤?推论⑴ 平分弦的直径垂直于弦,并且平分弦所对的两条弧。推论⑴ 平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。任意的弦AB都满足吗?A(2) ② ③ ① ④ ⑤?推论⑵ 弦的垂直平分线经过圆心,并且平分弦所对的两条弧。《数学》九(下)26.2圆的对称性(二)14探究还能得到哪些与上述不同的情况?OECDAB∟(3)① ④ ② ③ ⑤?(4)① ⑤ ② ③ ④?(5)② ④ ① ③ ⑤?(6)② ⑤ ① ③ ④?(7)③ ④ ① ② ⑤?(8)③ ⑤ ① ② ④?(9)④ ⑤ ① ② ③?《数学》九(下)26.2圆的对称性(二)15 1、如图:在⊙O中,AB为直径,CD为非直径的弦,对于(1)AB⊥CD (2)AB平分CD (3)AB平分CD所对的弧。若以其中的一个为条件,另两个为结论构成三个命题,其中真命题的个数为 ( )
A、3 B、2
C、1 D、0A练习《数学》九(下)26.2圆的对称性(二)16练习 2、如图:已知AB是⊙O的直径,弦CD与AB相交于点E,若 、
则CE=DE(只需填写一个你认为适当的条件)AB⊥CD第2题图第3题图2圆心到弦的距离叫做弦心距《数学》九(下)26.2圆的对称性(二)17在Rt△OAD中,由勾股定理,得解得 R≈27.9(m)答:赵州石拱桥的桥拱半径约为27.9米. AB=37.4m CD =7.2m例题4由垂径定理得:∴ ∴由题设可知:《数学》九(下)26.2圆的对称性(二)18问题1:如果两条弦所夹的弧相等,那么这两条弦一定平行吗?CDBA《数学》九(下)26.2圆的对称性(二)19问题2:已知:AB和CD是⊙O的两条弦,AB∥CD,AB=8cm,CD=6cm,⊙O的半径为5cm。(1)请根据题意画出符合条件的图形。
(2)求出AB与CD间的距离。EF=1cmEF=7cm《数学》九(下)26.2圆的对称性(二)20问题3:如图:图中是一个下水道的横截面。为了测量下水道的水深,先测得了水管的直径为10m,然后又测得了水面的宽度为8m。你能根据所提供的数据求得水深吗?《数学》九(下)26.2圆的对称性(二)211、垂径定理及其推论。 如图:对于一个圆中的弦长a、圆心距d、半径r、弓高h,这四个量中,只要已知其中任意两个量,就可以求出另外两个量。⑴ d + h = rrd本课小结常用的辅助线是过圆心作弦的垂线段(即弦心距)2、运用垂径定理及其推论解决有关几何问题。《数学》九(下)26.2圆的对称性(二)22 在我们生活中处处存在数学问题。 比如:某村在村口建一个如图形状的门楼,上半部是半圆拱,半径1.5米,圆心距地面2米。现有一辆高2.9米,宽2.5米的集装箱卡车,问能通过这个门楼吗?课后思考《数学》九(下)26.2圆的对称性(二)23再见《数学》九(下)26.2圆的对称性(二)24探究OECDAB(3)① ④ ② ③ ⑤?推论⑶ 平分弦所对优弧的直径垂直平分这条弦 ,并且平分这条弦所对的劣弧。(4)① ⑤ ② ③ ④?推论⑷ 平分弦所对劣弧的直径垂直平分这条弦 ,并且平分这条弦所对的优弧。推论 平分弦所对弧的直径垂直平分这条弦 ,并且平分这条弦所对的另一条弧。《数学》九(下)26.2圆的对称性(二)25探究OECDAB(5)② ④ ① ③ ⑤?推论⑸ 垂直于弦并且平分这条弦所对优弧的直线,经过圆心并且平分这条弦及这条弦所对的劣弧。(6)② ⑤ ① ③ ④?推论⑹ 垂直于弦并且平分这条弦所对劣弧的直线,经过圆心并且平分这条弦及这条弦所对的优弧。推论 垂直于弦并且平分这条弦所对一条弧的直线,经过圆心并且平分这条弦及这条弦所对的另一条弧。《数学》九(下)26.2圆的对称性(二)26探究OECDAB(7)③ ④ ① ② ⑤?推论⑺ 经过弦的中点并且平分这条弦所对优弧的直线,经过圆心并且垂直于这条弦及平分这条弦所对的劣弧。(8)③ ⑤ ① ② ④?推论⑻ 经过弦的中点并且平分这条弦所对劣弧的直线,经过圆心并且垂直于这条弦及平分这条弦所对的优弧。推论 经过弦的中点并且平分这条弦所对一条弧的直线,经过圆心并且垂直于这条弦及平分这条弦所对的另一条弧。《数学》九(下)26.2圆的对称性(二)27探究OECDAB(9)④ ⑤ ① ② ③?推论⑼ 平分一条弦所对两条弧的直线,经过圆心并且垂直平分这条弦。
还需要满足CD⊥AB才存在 如图2,AB是⊙O的弦,CD⊥AB,是否一定存在CD平分AB,CD平分弦AB所对的两条弧?BCDE不一定存在还需要满足什么条件?不一定存在还需要满足什么条件?当CD⊥AB 时,还需要满足CD是直径才存在当CD⊥AB 时,还需要满足CD过圆心才存在图1图2《数学》九(下)26.2圆的对称性(二)5条件结论CD为直径
CD⊥ABO分析CD平分AB(1)直径(过圆心的直线)
(2)垂直于弦 (3)平分弦(4)平分弦所对的劣弧(5)平分弦所对的优弧垂径定理《数学》九(下)26.2圆的对称性(二)6归纳垂径定理 垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧。1、文字语言2、数学语言∵ CD是⊙O的直径
CD⊥AB
∴ AE = EB
3、图形语言O《数学》九(下)26.2圆的对称性(二)7证明结论O证明:连结OA、OB,∴△OAB为等腰三角形∵ CD⊥AB∴△OAB底边AB上的高OE所在的直线CD是AB的垂直平分线∴点A、B关于直线CD对称则OA=OB。设点P是圆上任意一点,过点P作PQ⊥CD ,交⊙O于点Q,∴ AE=BE 已知:在⊙O中,CD是直径,AB是弦,CD⊥AB,垂足为E。 求证:AE=BE ,
。∴⊙O关于直线CD对称P同理 点P与点Q也关于直线CD对称Q《数学》九(下)26.2圆的对称性(二)82、请画图说明垂径定理的条件和结论。1、判断下列图是否是表示垂径定理的图形。是不是是O练习《数学》九(下)26.2圆的对称性(二)9垂径定理的几个基本图形《数学》九(下)26.2圆的对称性(二)10例1 如图,已知在⊙O中,弦AB的长为8厘米,圆心O到AB的距离为3厘米,求⊙O的半径。解:连结OA。过O作OE⊥AB,垂足为E例题1《数学》九(下)26.2圆的对称性(二)11例题2 已知:如图,在以O为圆心的两个同心圆中,大圆的弦AB交小圆于C,D两点。
求证:AC=BD。ABCD证明:过O作OE⊥AB,垂足为E∴ AE=BE CE=DE ∴ AE-CE=BE-DE∴ AC=BD?《数学》九(下)26.2圆的对称性(二)12MN例题3证明:作直径MN⊥AB∵ AB∥CD∴ MN⊥CD∟∴(垂直于弦的直径平分弦所对的弧)∴推论:
圆的两条平行弦所夹的弧相等数学语言:∵AB∥CD ∴《数学》九(下)26.2圆的对称性(二)13O探究ECDAB∟由垂径定理可知:
① ② ③ ④ ⑤(1)① ③ ② ④ ⑤?推论⑴ 平分弦的直径垂直于弦,并且平分弦所对的两条弧。推论⑴ 平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧。任意的弦AB都满足吗?A(2) ② ③ ① ④ ⑤?推论⑵ 弦的垂直平分线经过圆心,并且平分弦所对的两条弧。《数学》九(下)26.2圆的对称性(二)14探究还能得到哪些与上述不同的情况?OECDAB∟(3)① ④ ② ③ ⑤?(4)① ⑤ ② ③ ④?(5)② ④ ① ③ ⑤?(6)② ⑤ ① ③ ④?(7)③ ④ ① ② ⑤?(8)③ ⑤ ① ② ④?(9)④ ⑤ ① ② ③?《数学》九(下)26.2圆的对称性(二)15 1、如图:在⊙O中,AB为直径,CD为非直径的弦,对于(1)AB⊥CD (2)AB平分CD (3)AB平分CD所对的弧。若以其中的一个为条件,另两个为结论构成三个命题,其中真命题的个数为 ( )
A、3 B、2
C、1 D、0A练习《数学》九(下)26.2圆的对称性(二)16练习 2、如图:已知AB是⊙O的直径,弦CD与AB相交于点E,若 、
则CE=DE(只需填写一个你认为适当的条件)AB⊥CD第2题图第3题图2圆心到弦的距离叫做弦心距《数学》九(下)26.2圆的对称性(二)17在Rt△OAD中,由勾股定理,得解得 R≈27.9(m)答:赵州石拱桥的桥拱半径约为27.9米. AB=37.4m CD =7.2m例题4由垂径定理得:∴ ∴由题设可知:《数学》九(下)26.2圆的对称性(二)18问题1:如果两条弦所夹的弧相等,那么这两条弦一定平行吗?CDBA《数学》九(下)26.2圆的对称性(二)19问题2:已知:AB和CD是⊙O的两条弦,AB∥CD,AB=8cm,CD=6cm,⊙O的半径为5cm。(1)请根据题意画出符合条件的图形。
(2)求出AB与CD间的距离。EF=1cmEF=7cm《数学》九(下)26.2圆的对称性(二)20问题3:如图:图中是一个下水道的横截面。为了测量下水道的水深,先测得了水管的直径为10m,然后又测得了水面的宽度为8m。你能根据所提供的数据求得水深吗?《数学》九(下)26.2圆的对称性(二)211、垂径定理及其推论。 如图:对于一个圆中的弦长a、圆心距d、半径r、弓高h,这四个量中,只要已知其中任意两个量,就可以求出另外两个量。⑴ d + h = rrd本课小结常用的辅助线是过圆心作弦的垂线段(即弦心距)2、运用垂径定理及其推论解决有关几何问题。《数学》九(下)26.2圆的对称性(二)22 在我们生活中处处存在数学问题。 比如:某村在村口建一个如图形状的门楼,上半部是半圆拱,半径1.5米,圆心距地面2米。现有一辆高2.9米,宽2.5米的集装箱卡车,问能通过这个门楼吗?课后思考《数学》九(下)26.2圆的对称性(二)23再见《数学》九(下)26.2圆的对称性(二)24探究OECDAB(3)① ④ ② ③ ⑤?推论⑶ 平分弦所对优弧的直径垂直平分这条弦 ,并且平分这条弦所对的劣弧。(4)① ⑤ ② ③ ④?推论⑷ 平分弦所对劣弧的直径垂直平分这条弦 ,并且平分这条弦所对的优弧。推论 平分弦所对弧的直径垂直平分这条弦 ,并且平分这条弦所对的另一条弧。《数学》九(下)26.2圆的对称性(二)25探究OECDAB(5)② ④ ① ③ ⑤?推论⑸ 垂直于弦并且平分这条弦所对优弧的直线,经过圆心并且平分这条弦及这条弦所对的劣弧。(6)② ⑤ ① ③ ④?推论⑹ 垂直于弦并且平分这条弦所对劣弧的直线,经过圆心并且平分这条弦及这条弦所对的优弧。推论 垂直于弦并且平分这条弦所对一条弧的直线,经过圆心并且平分这条弦及这条弦所对的另一条弧。《数学》九(下)26.2圆的对称性(二)26探究OECDAB(7)③ ④ ① ② ⑤?推论⑺ 经过弦的中点并且平分这条弦所对优弧的直线,经过圆心并且垂直于这条弦及平分这条弦所对的劣弧。(8)③ ⑤ ① ② ④?推论⑻ 经过弦的中点并且平分这条弦所对劣弧的直线,经过圆心并且垂直于这条弦及平分这条弦所对的优弧。推论 经过弦的中点并且平分这条弦所对一条弧的直线,经过圆心并且垂直于这条弦及平分这条弦所对的另一条弧。《数学》九(下)26.2圆的对称性(二)27探究OECDAB(9)④ ⑤ ① ② ③?推论⑼ 平分一条弦所对两条弧的直线,经过圆心并且垂直平分这条弦。
