第六章 章未复习与提高 课件 高一下学期物理人教版(2019)必修第二册(共41张PPT)
文档属性
| 名称 | 第六章 章未复习与提高 课件 高一下学期物理人教版(2019)必修第二册(共41张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-04-14 10:25:37 | ||
图片预览






文档简介
(共41张PPT)
第六章
圆周运动
第六章 章未复习与提高
圆周运动
圆周运动
圆周运动
圆周运动
圆周运动
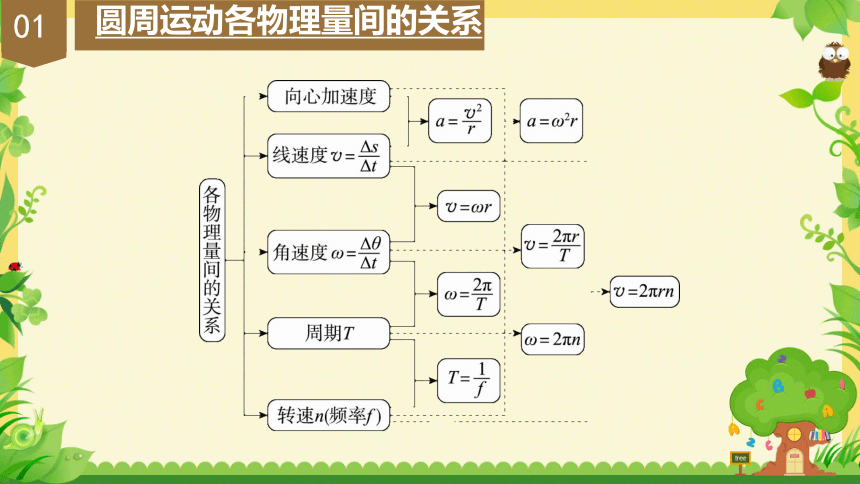
圆周运动各物理量间的关系
N
ω
O
N
G
f
T
G
o’
o
F
F
G
N
f
G
F
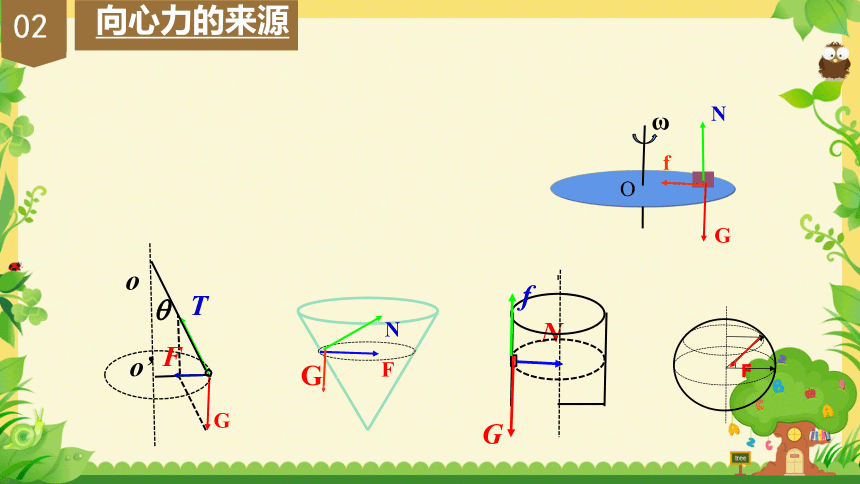
向心力的来源
竖直面
绳
环
杆
管
水平面
M
r
o
m
θ
ω
圆周运动的临界问题
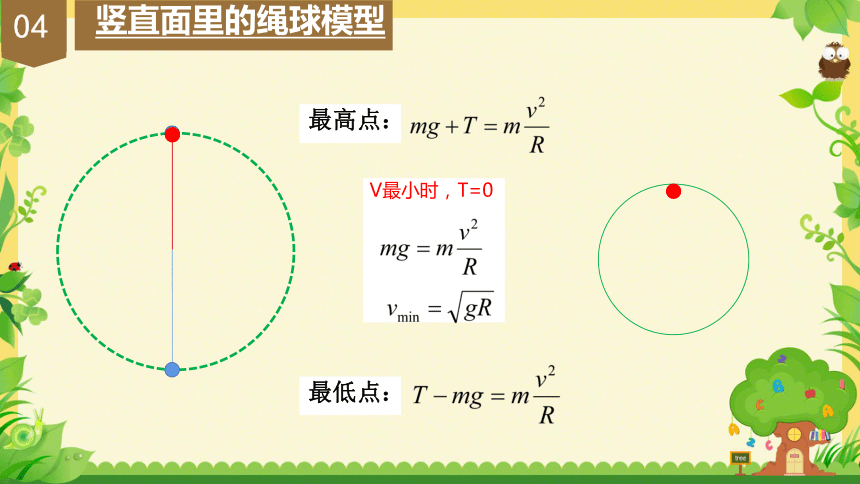
最高点:
最低点:
V最小时,T=0
竖直面里的绳球模型
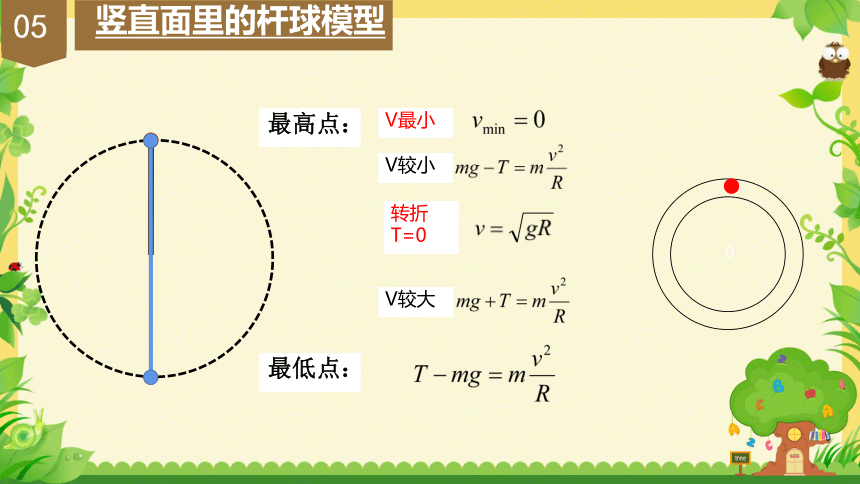
最高点:
0
最低点:
V较小
V最小
V较大
转折
T=0
竖直面里的杆球模型
O1
a
b
c
O2
Ra
Rc
Rb
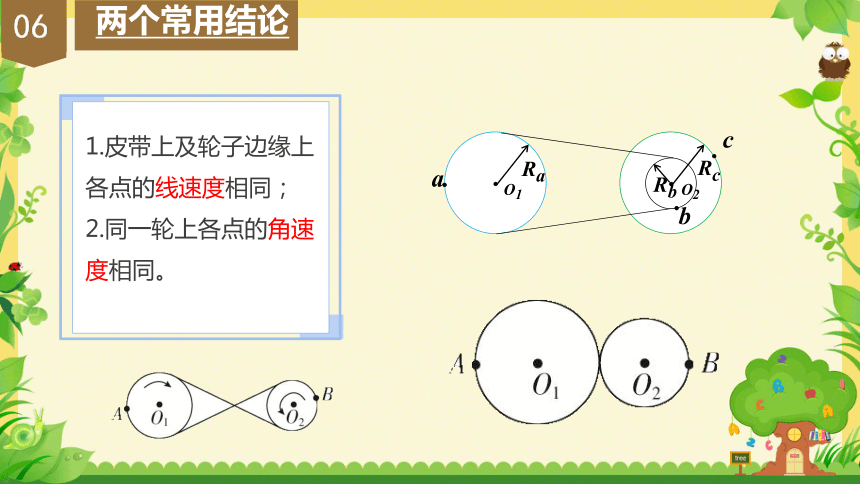
两个常用结论
1.皮带上及轮子边缘上各点的线速度相同;
2.同一轮上各点的角速度相同。
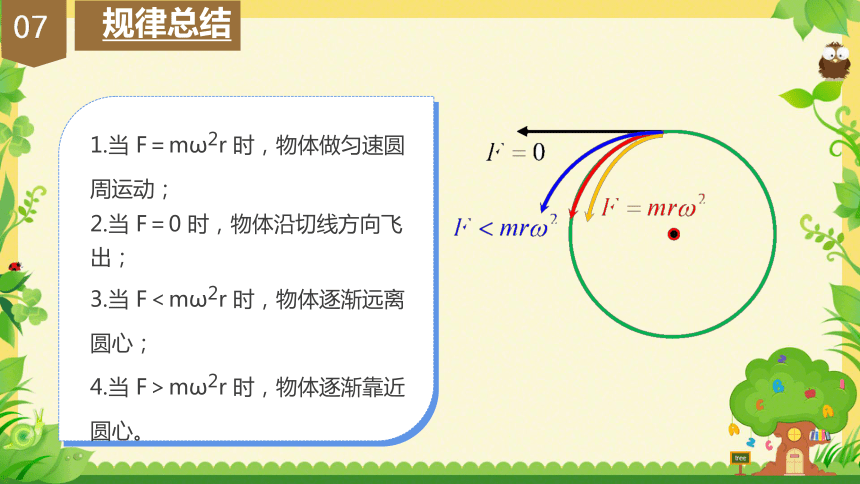
当 F=mω2r 时,物体做匀速圆周运动;
当 F=0 时,物体沿切线方向飞出;
当 F<mω2r 时,物体逐渐远离圆心;
当 F>mω2r 时,物体逐渐靠近圆心。
规律总结
斜面上的圆周运动
在斜面上做圆周运动的物体,因所受的控制因素不同,如静摩擦力控制、轻绳控制、轻杆控制,物体的受力情况和临界条件也不相同。(1)静摩擦力控制下的圆周运动
(2)轻绳控制下的圆周运动
(3)轻杆控制下的圆周运动
极限思想
思想方法
O
B
A
vA
vB
vA
Δv
Δθ
Δθ
Δt趋于0时,Δv 逐渐趋向于平行 OA,即Δv指向圆心,此时加速度a也指向圆心。
vA
O
A
B
vB
Δv
Δv
FN = G
G
FN
G
G
FN
FN
比较三种桥面的受力情况
圆锥摆的临界问题,主要就是与弹力有关的临界问题。
(1)绳上拉力的临界条件是:
①绳恰好拉直且没有弹力;②绳上的拉力恰好达最大值。
(2)接触或脱离的临界条件是物体与物体间的弹力恰好为零。
(3)对于火车转弯、半圆形碗内的水平圆周运动有两类临界情况: ①摩擦力的方向发生改变;②发生相对滑动。
解圆锥摆临界问题的技巧
复习与提高
A组
1.请根据加速度的特点,对以下七种运动进行分类,并画出分类的树状结构图:匀速直线运动;匀变速直线运动;自由落体运动;抛体运动;平抛运动;匀速圆周运动;变速圆周运动。
2.图6-1是一皮带传动装置的示意图,右轮半径为r,A是它边缘上的一点。左侧是一轮轴,大轮半径为4r,小轮半径为2r。B点在小轮上,到小轮中心的距离为r。C点和D点分别位于小轮和大轮的边缘上。如果传动过程中皮带不打滑,那么A、B、C、D点的线速度、角速度、向心加速度之比分别是多少
比较A、C:v相同
比较B、C、D:ω相同
2:1:2:4,
2:1:1:1;
4:1:2:4。
3.在空间站中,宇航员长期处于失重状态。为缓解这种状态带来的不适,科学家设想建造一种环形空间站,如图6-2所示。圆环绕中心匀速旋转,宇航员站在旋转舱内的侧壁上,可以受到与他站在地球表面时相同大小的支持力。已知地球表面的重力加速度为g,圆环的半径为r,宇航员可视为质点,为达到目的,旋转舱绕其轴线匀速转动的角速度应为多大
图6-2
宇航员站在地球表面时有FN=mg
要使宇航员站在旋转舱内侧壁上受到与他站在地球表面时相同大小的支持力,则有:
由此解得:
FN=mrω2
4.如图6-3所示,长L的轻杆两端分别固定着可以视为质点的小球A、B,放置在光滑水平桌面上,杆中心O有一竖直方向的固定转动轴,A、B的质量分别为3m、m。当轻杆以角速度ω绕轴在水平桌面上转动时,求转轴受杆拉力的大小。
对A球有:
对B球有:
又有:
A球对杆的拉力:
B球对杆的拉力:
转轴受到杆的拉力:
5.如图6-4所示,滚筒洗衣机脱水时,滚筒绕水平转动轴转动。滚筒上有很多漏水孔,滚筒转动时,附着在潮湿衣服上的水从漏水孔中被甩出,达到脱水的目的。如果认为湿衣服在竖直平面内做匀速圆周运动,那么,湿衣服上的水是在最低点还是最高点时更容易甩出 请说明道理。
滚筒洗衣机的脱水筒匀速旋转时,附着在筒壁上的衣服做圆周运动的向心力由重力和弹力的合力提供。
脱水筒匀速旋转时,附着在潮湿衣服上的水的重力mg和衣服与水之间的附着力(分子力)F的合力提供水的向心力。
在最高点有:
在最低点有:
对比最高点和最低点水的受力情况可知:
由此可见,在同一转速的情况下,水在最低点所受到的分子力更大,所以更容易在最低点从漏水孔甩出,做离心运动。
6.波轮洗衣机中的脱水筒(图6-5)在脱水时,衣服紧贴在筒壁上做匀速圆周运动。某洗衣机的有关规格如下表所示。在运行脱水程序时,有一质量m=6g的硬币被甩到桶壁上,随桶壁一起做匀速圆周运动。求桶壁对它的静摩擦力和弹力的大小。在解答本题时可以选择表格中有用的数据。g取10m/s2。
mg
Ff
FN
分析硬币的受力情况如图所示。
由表格中的数据可知,脱水桶的转速n=600r/min=10r/s,脱水桶的直径D=0.3m,则半径r=0.15m。在水平方向由弹力提供向心力,即FN =4π2mn2r,得FN=3.6N。
在竖直方向上,摩擦力与重力平衡,故Ff=mg=0.06N。
7.如图6-6所示,半径为R的半球形陶罐,固定在可以绕竖直轴转动的水平转台上,转台转轴与过陶罐球心O的对称轴OO'重合。转台以一定角速度匀速转动,一质量为m的小物块落入陶罐内,经过一段时间后小物块随陶罐一起转动且相对罐壁静止,此时小物块受到的摩擦力恰好为0,且它和O点的连线与OO'之间的夹角θ为60°,重力加速度为g。求转台转动的角速度。
mg
FN
F合
得:
复习与提高
B组
1.如图6-7所示,半径R=0.40m的光滑半圆环轨道处于竖直平面内,半圆环与水平地面相切于圆环的端点A。一小球从A点冲上竖直半圆环,沿轨道运动到B点飞出,最后落在水平地面上的C点(图上未画),g取10m/s2。
(1)能实现上述运动时,小球在B点的最小速度是多少
(2)能实现上述运动时,A、C间的最小距离是多少
(1)设小球通过B点的最小速度为v0,有:
解得:
(2)小球从B点水平飞出后做平抛运动,小球以最小速度平抛时距离最小,设小球做平抛运动的时间为t,AC间最小距离为x,则水平方向有:
由此解得t=0.4s,x=0.8m。
x=v0t
竖直方向有:
(1)质点做圆周运动的半径 ,角速度 ,向心加速度的大小
2.如图6-8所示,做匀速圆周运动的质点在时间t内由A点运
动到B点,AB所对的圆心角为θ,AB长为l。
(1)求质点向心加速度的大小。
(2)若某段时间内θ=60°,根据矢量的运算法则,求这段
时间内 与圆周运动的向心加速度的大小之比是多少
(2)如图所示,速度矢量三角形为等边三角形,因此有:
vA
vB
vA
△v
θ
θ
l
又有:
向心加速度:
与圆周运动的向心加速度的大小之比为:
3.如图6-9所示,带有一白点的灰色圆盘,绕过其中心且垂直于盘面的轴沿顺时针方向匀速转动,转速n=20r/s。在暗室中用每秒闪光21次的频闪光源照射圆盘,求观察到白点转动的方向和转动的周期。
θ
1
2
白光转动周期T1=1/20s,频闪周期T2=1/21s,设两次闪光间隔白点的位置如图所示,位置2相对位置1沿逆时针转过的角度:
所以观察到白点会逆时针转动。
白点转动角速度:
白点转动周期:
4.如图6-10所示,一长为l的轻杆的一端固定在水平转轴上,另一端固定一质量为m的小球,轻杆随转轴在竖直平面内做角速度为ω的匀速圆周运动,重力加速度为g。
(1)小球运动到最高点时,求杆对球的作用力。
(2)小球运动到水平位置A时,求杆对球的作用力。
(1)因转动的角速度大小未知,故小球在最高点时,杆对球的作用力F的方向不能确定。假设F1的方向竖直向下。根据F1+mg=mω2l ,解得F1=m(ω2l-g)。
①若 ,杆对小球的作用力为拉力,大小为F1=m(ω2l-g),方向竖直向下。
②若 ,F1=0,杆对小球恰好无作用力。
③若 ,杆对小球的作用力为支持力,大小为F1=m(g-ω2l),方向竖直向上。
(2)小球运动到水平位置A处时,杆对球的竖直方向分力Fy=mg,水平分力Fx=mω2l,故杆对球的作用力大小:
设该作用力与水平方向夹角为θ,则有:
故在位置A处杆对球的作用力方向斜向右上,与水平方向夹角为
5.如图6-11所示,质量为m的小球用细线悬于P点,使小球在水平面内做匀速圆周运动,重力加速度为g。
(1)若悬挂小球的绳长为l,小球做匀速圆周运动的角速度为ω,绳对小球的拉力F有多大
(2)若保持轨迹圆的圆心O到悬点P的距离h不变,改变绳长l,求小球做匀速圆周运动的角速度ω与绳长l的关系。
(3)若保持轨迹圆的圆心O到悬点P的距离h不变,改变绳长l,求绳对小球的拉力F与绳长l的关系。
mg
F
Fn
θ
θ
(1)如图所示,小球受到重力和沿细绳方向的拉力,设细绳与竖直方向的夹角为θ。沿水平方向有:Fn=Fsinθ=mω2lsinθ
解得细绳对小球的拉力:F=mω2l。
(2)小球受到重力和细绳拉力的合力指向圆心,有mg tan θ = mω2h tan θ,
解得: ,可见,轨迹圆的圆心O到悬点B的距离h不变,改变绳长l时,角速度ω保持不变,与绳长l无关。
(3)由第(1)(2)两问的结论F=mω2l和 , 解得 。可见,细绳的拉力F与绳长l成正比。
6.某人站在水平地面上,手握不可伸长的轻绳一端,绳的另一端系有质量为m的小球,使球在竖直平面内以手为圆心做圆周运动。当球某次运动到最低点时,绳恰好受到所能承受的最大拉力被拉断,球以绳断时的速度水平飞出,通过水平距离d后落地。已知握绳的手离地面高度为d,手与球之间的绳长为 ,重力加速度为g,忽略空气阻力。
(1)绳能承受的最大拉力是多少
(2)保持手的高度不变,改变绳长,使球重复上述运动,若绳仍在球运动到最低点时达到最大拉力被拉断,要使球抛出的水平距离最大,绳长应是多少 最大水平距离是多少
7.某场地自行车比赛圆形赛道的路面与水平面的
夹角为15°,sin15°=0.259,cos15°=0.966,不考虑
空气阻力,g取10 m/s2。
(1)运动员骑自行车在该赛道上做匀速圆周运动
(图6-12),圆周的半径为60m,要使自行车不受
摩擦力作用,其速度应等于多少
(2)若该运动员骑自行车以18m/s的速度仍沿该赛
道做匀速圆周运动,自行车和运动员的质量一共
是100kg,此时自行车所受摩擦力的大小又是多少 方向如何
巩固提升
【练习1】市面上有一种自动计数的智能呼拉圈深受女士们喜爱。如图甲,腰带外侧带有轨道,轨道内有一滑轮,滑轮与细绳连接,细绳的另一端连接配重,其模型简化如图乙所示.已知配重质量0.5kg,绳长为0.4m,悬挂点到腰带中心的距离为0.2m,水平固定好腰带,通过人体微小扭动,使配重在水平面内做匀速圆周运动,计数器显示在1min内圈数为120,此时绳子与竖直方向夹角为θ,配重运动过程中腰带可看做不动,g=10m/s2,sin37°=0.6,cos37°=0.8,下列说法正确的是( )
A.匀速转动时,配重受到的合力恒定不变
B.配重的角速度是240πrad/s
C.θ为37°
D.若增大转速,细绳拉力变大
【参考答案】D
课堂练习
【练习2】自行车的大齿轮、小齿轮、后轮三个轮子的边缘上有A、B、C三点,向心加速度随半径变化图像如图所示,则( )
A.A、B两点加速度关系满足甲图线
B.A、B两点加速度关系满足乙图线
C.A、C两点加速度关系满足甲图线
D.A、C两点加速度关系满足乙图线
【参考答案】A
课堂练习
【练习3】2022年北京冬奥会后,滑雪已然成为了冬天最受大家欢迎的体育项目。如图甲所示,整体质量为m的单板滑雪爱好者在安全速降过程中获得了最大速度为v,为了顺利通过一个半径为R的水平弯道,滑雪者尝试以雪板紧贴弯道侧壁的方式过弯。如图乙所示,此侧壁与水平面的夹角为θ,此时滑雪板所受支持力大小为F,两侧面不受力,该弯道回转半径R远大于滑雪者的身高,重力加速度大小为g,不计空气与摩擦阻力影响,下列说法正确的是( )
A. B.
C. D.
【参考答案】A
课堂练习
【练习4】如图为某型号圆锥面型娱乐设施“魔盘”的侧视图,“魔盘”可绕中心轴OO 转动。儿童坐在锥面上,“魔盘”从静止开始转动,转速逐渐增大。最大静摩擦跟正压力成正比,儿童可视为质点,下列说法正确的是( )
A.玩乐的过程中,儿童受到的合外力方向时刻水平指向转轴
B.其他条件相同时,儿童的质量越大越容易滑动
C.当“魔盘”的转速增大到一定值时,儿童一定会向上滑动
D.“魔盘”加速转动的过程,儿童未发生滑动时,受到的摩擦力可能减小
【参考答案】D
课堂练习
【练习5】(多选)如图所示为向心力演示仪,质量相同的钢球①、②分别固定在A、B盘的边缘,A、B两盘的半径之比为3:1,a、b分别是与A盘、B盘一起同轴转动的轮,a、b轮半径之比为1:3,a、b两轮在同一皮带带动下匀速转动,且皮带与轮间不打滑,下列说法正确的是( )
A.钢球①、②角速度大小之比ω1:ω2=3:1
B.钢球①、②线速度大小之比v1:v2=3:1
C.钢球①、②加速度大小之比a1:a2=27:1
D.钢球①、②受到的向心力大小之比F1:F2=1:1
【参考答案】AC
【练习6】如图所示,两个质量分别为m、2m的小木块a和b(可视为质点)放在水平圆盘上,a与转轴OO′的距离为l,b与转轴OO′的距离为2l,两木块与圆盘间的最大静摩擦力均为木块所受重力的k倍,重力加速度大小为g。若圆盘从静止开始绕转轴缓慢地加速转动,用ω表示圆盘转动的角速度,下列说法正确的是( )
A.a、b相对圆盘刚开始滑动时的临界角速度大小之比为ω1 :ω2 = :1
B.a、b相对圆盘有沿半径向外运动的趋势
C. 是a开始滑动的临界角速度
D.当 时,b所受摩擦力的大小为kmg
【参考答案】A
【练习7】(多选)如图所示,质量为M = 4kg、半径R = 0.6m的光滑细圆管用轻杆固定在竖直平面内,小球A和B的直径略小于细圆管的内径,它们的质量分别为mA= 1kg,mB= 2kg。某时刻,小球A、B分别位于圆管最低点和最高点,且A的速度大小为vA= 3m/s,此时竖直轻杆受到细圆管的作用力大小为F = 55N。则B球的速度vB大小为(取g = 10m/s2)( )
A.3m/s B. C.6m/s D.
【参考答案】AD
【练习8】如图所示,一个质量为60kg的滑板运动员,以 的初速度从某一高台的A点水平飞出,恰好从圆轨道的B点的切线方向进入圆弧(不计空气阻力,进入圆弧时无机械能损失),最终滑板运动员刚好到达圆轨道的最高点D。已知圆弧的半径R=3m, ,取g = 10m/s2,求:
(1)A距C点的高度和滑板运动员在D点的速度大小。
(2)若滑板运动员运动到圆弧轨道点C时的速度大小
为15m/s则滑板运动员对轨道的压力。
课堂练习
课堂练习
第六章
圆周运动
第六章 章未复习与提高
圆周运动
圆周运动
圆周运动
圆周运动
圆周运动
圆周运动各物理量间的关系
N
ω
O
N
G
f
T
G
o’
o
F
F
G
N
f
G
F
向心力的来源
竖直面
绳
环
杆
管
水平面
M
r
o
m
θ
ω
圆周运动的临界问题
最高点:
最低点:
V最小时,T=0
竖直面里的绳球模型
最高点:
0
最低点:
V较小
V最小
V较大
转折
T=0
竖直面里的杆球模型
O1
a
b
c
O2
Ra
Rc
Rb
两个常用结论
1.皮带上及轮子边缘上各点的线速度相同;
2.同一轮上各点的角速度相同。
当 F=mω2r 时,物体做匀速圆周运动;
当 F=0 时,物体沿切线方向飞出;
当 F<mω2r 时,物体逐渐远离圆心;
当 F>mω2r 时,物体逐渐靠近圆心。
规律总结
斜面上的圆周运动
在斜面上做圆周运动的物体,因所受的控制因素不同,如静摩擦力控制、轻绳控制、轻杆控制,物体的受力情况和临界条件也不相同。(1)静摩擦力控制下的圆周运动
(2)轻绳控制下的圆周运动
(3)轻杆控制下的圆周运动
极限思想
思想方法
O
B
A
vA
vB
vA
Δv
Δθ
Δθ
Δt趋于0时,Δv 逐渐趋向于平行 OA,即Δv指向圆心,此时加速度a也指向圆心。
vA
O
A
B
vB
Δv
Δv
FN = G
G
FN
G
G
FN
FN
比较三种桥面的受力情况
圆锥摆的临界问题,主要就是与弹力有关的临界问题。
(1)绳上拉力的临界条件是:
①绳恰好拉直且没有弹力;②绳上的拉力恰好达最大值。
(2)接触或脱离的临界条件是物体与物体间的弹力恰好为零。
(3)对于火车转弯、半圆形碗内的水平圆周运动有两类临界情况: ①摩擦力的方向发生改变;②发生相对滑动。
解圆锥摆临界问题的技巧
复习与提高
A组
1.请根据加速度的特点,对以下七种运动进行分类,并画出分类的树状结构图:匀速直线运动;匀变速直线运动;自由落体运动;抛体运动;平抛运动;匀速圆周运动;变速圆周运动。
2.图6-1是一皮带传动装置的示意图,右轮半径为r,A是它边缘上的一点。左侧是一轮轴,大轮半径为4r,小轮半径为2r。B点在小轮上,到小轮中心的距离为r。C点和D点分别位于小轮和大轮的边缘上。如果传动过程中皮带不打滑,那么A、B、C、D点的线速度、角速度、向心加速度之比分别是多少
比较A、C:v相同
比较B、C、D:ω相同
2:1:2:4,
2:1:1:1;
4:1:2:4。
3.在空间站中,宇航员长期处于失重状态。为缓解这种状态带来的不适,科学家设想建造一种环形空间站,如图6-2所示。圆环绕中心匀速旋转,宇航员站在旋转舱内的侧壁上,可以受到与他站在地球表面时相同大小的支持力。已知地球表面的重力加速度为g,圆环的半径为r,宇航员可视为质点,为达到目的,旋转舱绕其轴线匀速转动的角速度应为多大
图6-2
宇航员站在地球表面时有FN=mg
要使宇航员站在旋转舱内侧壁上受到与他站在地球表面时相同大小的支持力,则有:
由此解得:
FN=mrω2
4.如图6-3所示,长L的轻杆两端分别固定着可以视为质点的小球A、B,放置在光滑水平桌面上,杆中心O有一竖直方向的固定转动轴,A、B的质量分别为3m、m。当轻杆以角速度ω绕轴在水平桌面上转动时,求转轴受杆拉力的大小。
对A球有:
对B球有:
又有:
A球对杆的拉力:
B球对杆的拉力:
转轴受到杆的拉力:
5.如图6-4所示,滚筒洗衣机脱水时,滚筒绕水平转动轴转动。滚筒上有很多漏水孔,滚筒转动时,附着在潮湿衣服上的水从漏水孔中被甩出,达到脱水的目的。如果认为湿衣服在竖直平面内做匀速圆周运动,那么,湿衣服上的水是在最低点还是最高点时更容易甩出 请说明道理。
滚筒洗衣机的脱水筒匀速旋转时,附着在筒壁上的衣服做圆周运动的向心力由重力和弹力的合力提供。
脱水筒匀速旋转时,附着在潮湿衣服上的水的重力mg和衣服与水之间的附着力(分子力)F的合力提供水的向心力。
在最高点有:
在最低点有:
对比最高点和最低点水的受力情况可知:
由此可见,在同一转速的情况下,水在最低点所受到的分子力更大,所以更容易在最低点从漏水孔甩出,做离心运动。
6.波轮洗衣机中的脱水筒(图6-5)在脱水时,衣服紧贴在筒壁上做匀速圆周运动。某洗衣机的有关规格如下表所示。在运行脱水程序时,有一质量m=6g的硬币被甩到桶壁上,随桶壁一起做匀速圆周运动。求桶壁对它的静摩擦力和弹力的大小。在解答本题时可以选择表格中有用的数据。g取10m/s2。
mg
Ff
FN
分析硬币的受力情况如图所示。
由表格中的数据可知,脱水桶的转速n=600r/min=10r/s,脱水桶的直径D=0.3m,则半径r=0.15m。在水平方向由弹力提供向心力,即FN =4π2mn2r,得FN=3.6N。
在竖直方向上,摩擦力与重力平衡,故Ff=mg=0.06N。
7.如图6-6所示,半径为R的半球形陶罐,固定在可以绕竖直轴转动的水平转台上,转台转轴与过陶罐球心O的对称轴OO'重合。转台以一定角速度匀速转动,一质量为m的小物块落入陶罐内,经过一段时间后小物块随陶罐一起转动且相对罐壁静止,此时小物块受到的摩擦力恰好为0,且它和O点的连线与OO'之间的夹角θ为60°,重力加速度为g。求转台转动的角速度。
mg
FN
F合
得:
复习与提高
B组
1.如图6-7所示,半径R=0.40m的光滑半圆环轨道处于竖直平面内,半圆环与水平地面相切于圆环的端点A。一小球从A点冲上竖直半圆环,沿轨道运动到B点飞出,最后落在水平地面上的C点(图上未画),g取10m/s2。
(1)能实现上述运动时,小球在B点的最小速度是多少
(2)能实现上述运动时,A、C间的最小距离是多少
(1)设小球通过B点的最小速度为v0,有:
解得:
(2)小球从B点水平飞出后做平抛运动,小球以最小速度平抛时距离最小,设小球做平抛运动的时间为t,AC间最小距离为x,则水平方向有:
由此解得t=0.4s,x=0.8m。
x=v0t
竖直方向有:
(1)质点做圆周运动的半径 ,角速度 ,向心加速度的大小
2.如图6-8所示,做匀速圆周运动的质点在时间t内由A点运
动到B点,AB所对的圆心角为θ,AB长为l。
(1)求质点向心加速度的大小。
(2)若某段时间内θ=60°,根据矢量的运算法则,求这段
时间内 与圆周运动的向心加速度的大小之比是多少
(2)如图所示,速度矢量三角形为等边三角形,因此有:
vA
vB
vA
△v
θ
θ
l
又有:
向心加速度:
与圆周运动的向心加速度的大小之比为:
3.如图6-9所示,带有一白点的灰色圆盘,绕过其中心且垂直于盘面的轴沿顺时针方向匀速转动,转速n=20r/s。在暗室中用每秒闪光21次的频闪光源照射圆盘,求观察到白点转动的方向和转动的周期。
θ
1
2
白光转动周期T1=1/20s,频闪周期T2=1/21s,设两次闪光间隔白点的位置如图所示,位置2相对位置1沿逆时针转过的角度:
所以观察到白点会逆时针转动。
白点转动角速度:
白点转动周期:
4.如图6-10所示,一长为l的轻杆的一端固定在水平转轴上,另一端固定一质量为m的小球,轻杆随转轴在竖直平面内做角速度为ω的匀速圆周运动,重力加速度为g。
(1)小球运动到最高点时,求杆对球的作用力。
(2)小球运动到水平位置A时,求杆对球的作用力。
(1)因转动的角速度大小未知,故小球在最高点时,杆对球的作用力F的方向不能确定。假设F1的方向竖直向下。根据F1+mg=mω2l ,解得F1=m(ω2l-g)。
①若 ,杆对小球的作用力为拉力,大小为F1=m(ω2l-g),方向竖直向下。
②若 ,F1=0,杆对小球恰好无作用力。
③若 ,杆对小球的作用力为支持力,大小为F1=m(g-ω2l),方向竖直向上。
(2)小球运动到水平位置A处时,杆对球的竖直方向分力Fy=mg,水平分力Fx=mω2l,故杆对球的作用力大小:
设该作用力与水平方向夹角为θ,则有:
故在位置A处杆对球的作用力方向斜向右上,与水平方向夹角为
5.如图6-11所示,质量为m的小球用细线悬于P点,使小球在水平面内做匀速圆周运动,重力加速度为g。
(1)若悬挂小球的绳长为l,小球做匀速圆周运动的角速度为ω,绳对小球的拉力F有多大
(2)若保持轨迹圆的圆心O到悬点P的距离h不变,改变绳长l,求小球做匀速圆周运动的角速度ω与绳长l的关系。
(3)若保持轨迹圆的圆心O到悬点P的距离h不变,改变绳长l,求绳对小球的拉力F与绳长l的关系。
mg
F
Fn
θ
θ
(1)如图所示,小球受到重力和沿细绳方向的拉力,设细绳与竖直方向的夹角为θ。沿水平方向有:Fn=Fsinθ=mω2lsinθ
解得细绳对小球的拉力:F=mω2l。
(2)小球受到重力和细绳拉力的合力指向圆心,有mg tan θ = mω2h tan θ,
解得: ,可见,轨迹圆的圆心O到悬点B的距离h不变,改变绳长l时,角速度ω保持不变,与绳长l无关。
(3)由第(1)(2)两问的结论F=mω2l和 , 解得 。可见,细绳的拉力F与绳长l成正比。
6.某人站在水平地面上,手握不可伸长的轻绳一端,绳的另一端系有质量为m的小球,使球在竖直平面内以手为圆心做圆周运动。当球某次运动到最低点时,绳恰好受到所能承受的最大拉力被拉断,球以绳断时的速度水平飞出,通过水平距离d后落地。已知握绳的手离地面高度为d,手与球之间的绳长为 ,重力加速度为g,忽略空气阻力。
(1)绳能承受的最大拉力是多少
(2)保持手的高度不变,改变绳长,使球重复上述运动,若绳仍在球运动到最低点时达到最大拉力被拉断,要使球抛出的水平距离最大,绳长应是多少 最大水平距离是多少
7.某场地自行车比赛圆形赛道的路面与水平面的
夹角为15°,sin15°=0.259,cos15°=0.966,不考虑
空气阻力,g取10 m/s2。
(1)运动员骑自行车在该赛道上做匀速圆周运动
(图6-12),圆周的半径为60m,要使自行车不受
摩擦力作用,其速度应等于多少
(2)若该运动员骑自行车以18m/s的速度仍沿该赛
道做匀速圆周运动,自行车和运动员的质量一共
是100kg,此时自行车所受摩擦力的大小又是多少 方向如何
巩固提升
【练习1】市面上有一种自动计数的智能呼拉圈深受女士们喜爱。如图甲,腰带外侧带有轨道,轨道内有一滑轮,滑轮与细绳连接,细绳的另一端连接配重,其模型简化如图乙所示.已知配重质量0.5kg,绳长为0.4m,悬挂点到腰带中心的距离为0.2m,水平固定好腰带,通过人体微小扭动,使配重在水平面内做匀速圆周运动,计数器显示在1min内圈数为120,此时绳子与竖直方向夹角为θ,配重运动过程中腰带可看做不动,g=10m/s2,sin37°=0.6,cos37°=0.8,下列说法正确的是( )
A.匀速转动时,配重受到的合力恒定不变
B.配重的角速度是240πrad/s
C.θ为37°
D.若增大转速,细绳拉力变大
【参考答案】D
课堂练习
【练习2】自行车的大齿轮、小齿轮、后轮三个轮子的边缘上有A、B、C三点,向心加速度随半径变化图像如图所示,则( )
A.A、B两点加速度关系满足甲图线
B.A、B两点加速度关系满足乙图线
C.A、C两点加速度关系满足甲图线
D.A、C两点加速度关系满足乙图线
【参考答案】A
课堂练习
【练习3】2022年北京冬奥会后,滑雪已然成为了冬天最受大家欢迎的体育项目。如图甲所示,整体质量为m的单板滑雪爱好者在安全速降过程中获得了最大速度为v,为了顺利通过一个半径为R的水平弯道,滑雪者尝试以雪板紧贴弯道侧壁的方式过弯。如图乙所示,此侧壁与水平面的夹角为θ,此时滑雪板所受支持力大小为F,两侧面不受力,该弯道回转半径R远大于滑雪者的身高,重力加速度大小为g,不计空气与摩擦阻力影响,下列说法正确的是( )
A. B.
C. D.
【参考答案】A
课堂练习
【练习4】如图为某型号圆锥面型娱乐设施“魔盘”的侧视图,“魔盘”可绕中心轴OO 转动。儿童坐在锥面上,“魔盘”从静止开始转动,转速逐渐增大。最大静摩擦跟正压力成正比,儿童可视为质点,下列说法正确的是( )
A.玩乐的过程中,儿童受到的合外力方向时刻水平指向转轴
B.其他条件相同时,儿童的质量越大越容易滑动
C.当“魔盘”的转速增大到一定值时,儿童一定会向上滑动
D.“魔盘”加速转动的过程,儿童未发生滑动时,受到的摩擦力可能减小
【参考答案】D
课堂练习
【练习5】(多选)如图所示为向心力演示仪,质量相同的钢球①、②分别固定在A、B盘的边缘,A、B两盘的半径之比为3:1,a、b分别是与A盘、B盘一起同轴转动的轮,a、b轮半径之比为1:3,a、b两轮在同一皮带带动下匀速转动,且皮带与轮间不打滑,下列说法正确的是( )
A.钢球①、②角速度大小之比ω1:ω2=3:1
B.钢球①、②线速度大小之比v1:v2=3:1
C.钢球①、②加速度大小之比a1:a2=27:1
D.钢球①、②受到的向心力大小之比F1:F2=1:1
【参考答案】AC
【练习6】如图所示,两个质量分别为m、2m的小木块a和b(可视为质点)放在水平圆盘上,a与转轴OO′的距离为l,b与转轴OO′的距离为2l,两木块与圆盘间的最大静摩擦力均为木块所受重力的k倍,重力加速度大小为g。若圆盘从静止开始绕转轴缓慢地加速转动,用ω表示圆盘转动的角速度,下列说法正确的是( )
A.a、b相对圆盘刚开始滑动时的临界角速度大小之比为ω1 :ω2 = :1
B.a、b相对圆盘有沿半径向外运动的趋势
C. 是a开始滑动的临界角速度
D.当 时,b所受摩擦力的大小为kmg
【参考答案】A
【练习7】(多选)如图所示,质量为M = 4kg、半径R = 0.6m的光滑细圆管用轻杆固定在竖直平面内,小球A和B的直径略小于细圆管的内径,它们的质量分别为mA= 1kg,mB= 2kg。某时刻,小球A、B分别位于圆管最低点和最高点,且A的速度大小为vA= 3m/s,此时竖直轻杆受到细圆管的作用力大小为F = 55N。则B球的速度vB大小为(取g = 10m/s2)( )
A.3m/s B. C.6m/s D.
【参考答案】AD
【练习8】如图所示,一个质量为60kg的滑板运动员,以 的初速度从某一高台的A点水平飞出,恰好从圆轨道的B点的切线方向进入圆弧(不计空气阻力,进入圆弧时无机械能损失),最终滑板运动员刚好到达圆轨道的最高点D。已知圆弧的半径R=3m, ,取g = 10m/s2,求:
(1)A距C点的高度和滑板运动员在D点的速度大小。
(2)若滑板运动员运动到圆弧轨道点C时的速度大小
为15m/s则滑板运动员对轨道的压力。
课堂练习
课堂练习
