第3单元长方体和正方体素养检测卷-2024-2025学年数学五年级下册人教版(含解析)
文档属性
| 名称 | 第3单元长方体和正方体素养检测卷-2024-2025学年数学五年级下册人教版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 303.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-14 11:10:33 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
第3单元长方体和正方体素养检测卷-2024-2025学年数学五年级下册人教版
一、选择题
1.下面可以算出正方体体积的公式有( )。
A.棱长×棱长×棱长
B.长×宽×高
C.底面积×高
D.以上都可以
2.如图与4号面相对的面是( )。
A.1 B.2 C.3 D.6
3.一个长方体右面的面积是56cm2,长是7cm,高是6cm。要计算这个长方体的体积,正确的算式是( )。
A.6×7 B.56×6 C.56×7 D.56×6×7
4.如图是一个长方体,与棱h平行的棱一共有( )条。
A.1 B.2 C.3 D.4
5.一个棱长为8的正方体,由若干个棱长为1的小正方体组成,那么这个大正方体含有( )个这样的小正方体。
A.296 B.384 C.328 D.512
6.正方体的棱长扩大2倍,表面积扩大到原来的( )倍,体积扩大到原来的( )倍。括号里依次应填入( )。
A.2;8 B.4;8 C.6;8 D.8;4
二、填空题
7.填一填。
3升40毫升=( )升 8.25时=( )分 5.04平方千米=( )公顷
8.(如图)用彩带包扎一个长40cm、宽20cm、高18cm的长方体礼盒。打结处用了彩带15cm,包装这个礼盒共用彩带( )。
9.如图,墙角堆放一些棱长5cm的正方体,露在外面的面的面积是( )cm2。
10.一个能容纳128L水的长方体桶,高0.64m,它的底面积是( )。
11.一个长方体,如果高减少就变成了一个正方体,这时表面积就减少,原来长方体的表面积是( )。
12.一个底面积是100平方厘米的正方体容器,最多能装( )L水。
三、判断题
13.至少用4个小正方体就可以拼成一个大正方体。( )
14.棱长是9cm的正方体,它的体积大于表面积。( )
15.李师傅家的冰箱容积有220毫升。( )
16.棱长为6cm的正方体表面积和体积相等。( )
17.一个正方体玻璃鱼缸的棱长是6分米,求制作这个鱼缸至少需要多少平方分米玻璃,就是求这个鱼缸的表面积是多少。( )
四、计算题
18.直接写出得数。
0.7×100= 12.5×0.8= 0.25×4= 9.8÷0.01= 3.4+13=
0.36÷0.12= 350÷50= 10-9.12= 0.23= 2×0.1÷2×0.1=
19.按要求计算。
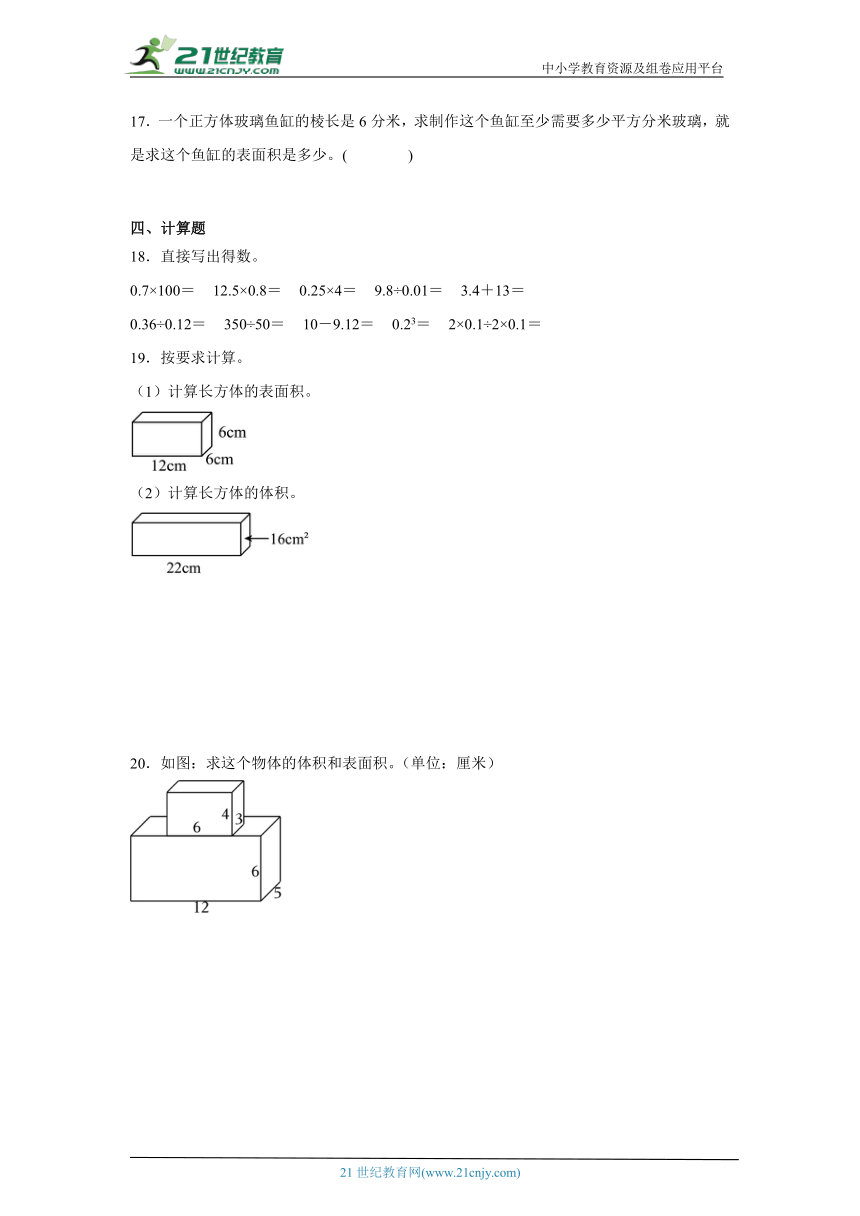
(1)计算长方体的表面积。
(2)计算长方体的体积。
20.如图:求这个物体的体积和表面积。(单位:厘米)
五、解答题
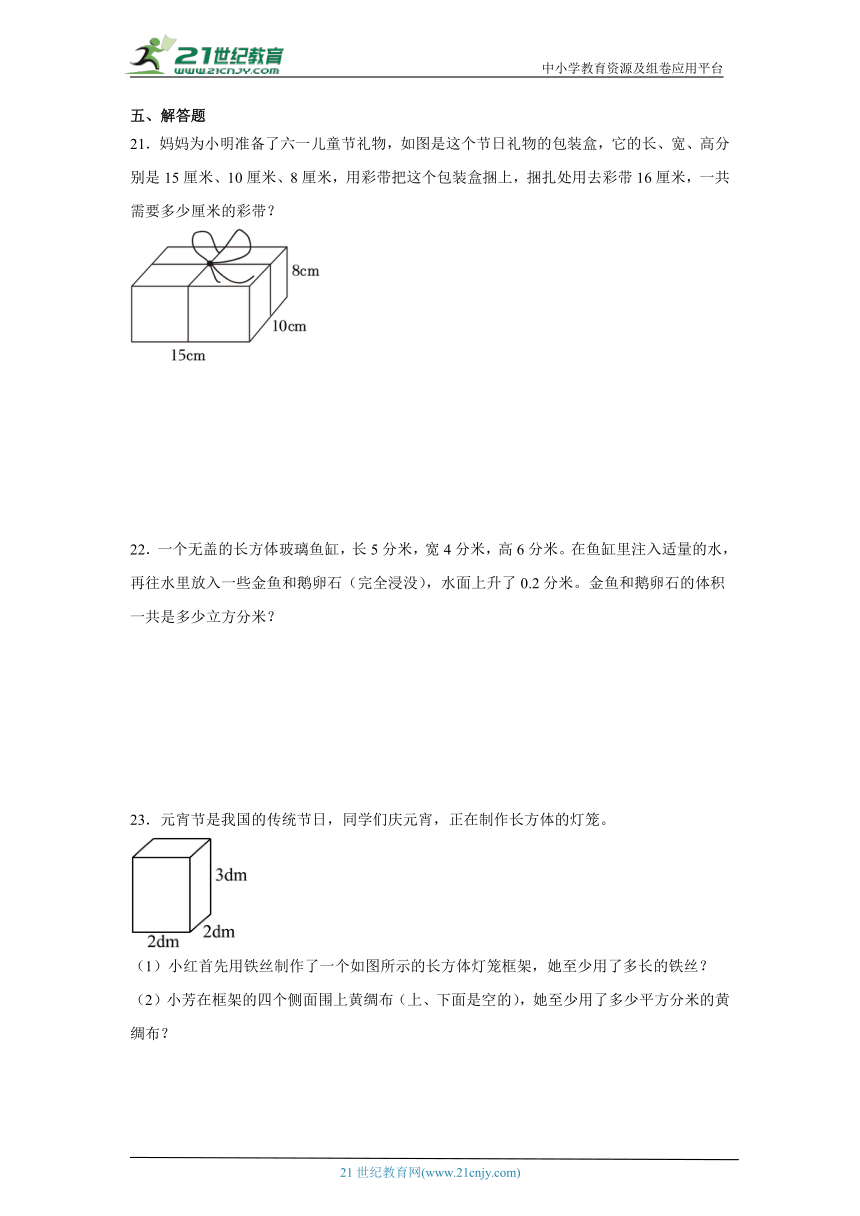
21.妈妈为小明准备了六一儿童节礼物,如图是这个节日礼物的包装盒,它的长、宽、高分别是15厘米、10厘米、8厘米,用彩带把这个包装盒捆上,捆扎处用去彩带16厘米,一共需要多少厘米的彩带?
22.一个无盖的长方体玻璃鱼缸,长5分米,宽4分米,高6分米。在鱼缸里注入适量的水,再往水里放入一些金鱼和鹅卵石(完全浸没),水面上升了0.2分米。金鱼和鹅卵石的体积一共是多少立方分米?
23.元宵节是我国的传统节日,同学们庆元宵,正在制作长方体的灯笼。
(1)小红首先用铁丝制作了一个如图所示的长方体灯笼框架,她至少用了多长的铁丝?
(2)小芳在框架的四个侧面围上黄绸布(上、下面是空的),她至少用了多少平方分米的黄绸布?
24.一个长方体水池从里面量长15分米,宽6分米,高10分米。
(1)如果把这个水池的四周及底部贴上瓷砖,那么需要贴瓷砖的面积是多少?
(2)如果要往这个水池里注入5分米深的水,那么需要多少升水?
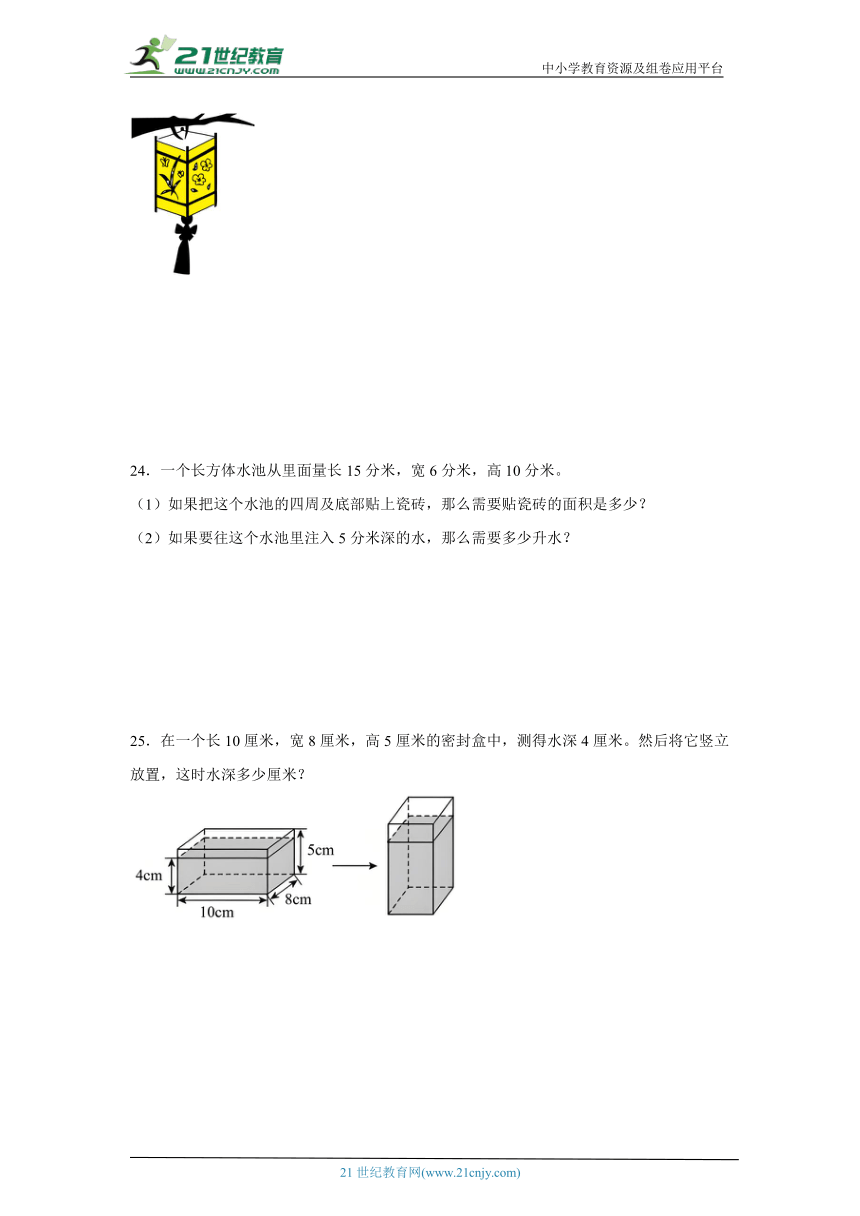
25.在一个长10厘米,宽8厘米,高5厘米的密封盒中,测得水深4厘米。然后将它竖立放置,这时水深多少厘米?
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
《第3单元长方体和正方体素养检测卷-2024-2025学年数学五年级下册人教版》参考答案
题号 1 2 3 4 5 6
答案 D C C C D B
1.D
【分析】根据,及,逐项分析。
【详解】A.根据正方体的体积公式可知,该选项符合题意。
B.正方体是长、宽、高相等的长方体,所以长×宽×高即棱长×棱长×棱长,该选项符合题意。
C.底面积为棱长×棱长,高等于棱长,乘积仍与棱长×棱长×棱长相等,该选项符合题意。
选项A、B、C都可以算出正方体体积。
故答案为:D
2.C
【分析】据图可知,这是“1-3-2”型正方体展开图,可以把4号面看作下面,则5号面和1号面是左右面,2号面和6号面是前后面,3号面和4号面是上下面,据此解答。
【详解】据图可知,6号面和2号面相对,1号面和5号面相对,4号面和3号面相对。
故答案为:C
3.C
【分析】分析题目,长方体右面的面积=宽×高,根据长方体的体积=长×宽×高可知:长方体的体积=右面的面积×长,据此解答。
【详解】56×7=392(cm3)
一个长方体右面的面积是56cm2,长是7cm,高是6cm。要计算这个长方体的体积,正确的算式是56×7。
故答案为:C
4.C
【分析】长方体有12条棱,相对的四条棱长度相等,按长度可分为三组,每一组有4条棱。
【详解】如图:
与棱h平行的棱分别是AB、CD、EF,一共有3条。
故答案为:C
5.D
【分析】根据正方体的体积=棱长×棱长×棱长,分别求出大、小正方体的体积,再相除即可求出小正方体的个数。
【详解】(8×8×8)÷(1×1×1)
=512÷1
=512(个)
这个大正方体含有512个这样的小正方体。
故答案为:D
6.B
【分析】根据正方体的表面积=棱长×棱长×6,正方体的体积=棱长×棱长×棱长可知,正方体的棱长扩大2倍,表面积扩大到原来的(2×2)倍,体积扩大到原来的(2×2×2)倍,据此解答。
【详解】2×2=4
2×2×2=8
正方体的棱长扩大2倍,表面积扩大到原来的4倍,体积扩大到原来的8倍。
故答案为:B
7. 3.04// 495 504
【分析】根据1升=1000毫升,1时=60分,1平方千米=100公顷,把高级单位的名数换算成低级单位的名数,就乘单位间的进率,把低级单位的名数换算成高级单位的名数,就除以单位间的进率。复名数换单名数,单位相同的不用换,单位不同的先统一单位,再加上之前没换单位部分的数,据此解答。
【详解】
(升)或(升)或(升)
(分)
(公顷)
3升40毫升=3.4(或或)升 8.25时=495分 5.04平方千米=504公顷
8.207cm/207厘米
【分析】观察图形可知,包装这个礼盒至少需要彩带的长度=2条长+2条宽+4条高+打结用的长度,据此解答。
【详解】40×2+20×2+18×4+15
=80+40+72+15
=207(cm)
包装这个礼盒共用彩带207cm。
9.225
【分析】分析题目,露在外面的面的面积=露在外面的面的个数×一个面的面积,据此先数出露在外面的一共有几个面,再根据棱长×棱长求出一个面的面积,最后求出它们的乘积即可。
【详解】9×(5×5)
=9×25
=225(cm2)
墙角堆放一些棱长5cm的正方体,露在外面的面的面积是225cm2。
10.0.2 m2
【分析】1L=1dm3,1m3=1000dm3;根据长方体的体积(容积)公式:v=sh,那么s=v÷h,用水的体积除以长方体水桶的高即可解答。
【详解】128L=128dm3=0.128m3
0.128÷0.64=0.2()
所以,它的底面积是0.2 。
11.480
【分析】一个长方体如果高减少3cm就变成一个正方体,说明原来长方体的长和宽相等;高减少3cm,表面积就减少96cm2,则减少的表面积就是4个相同的长方形的面积之和,用96除以4求出一个面的面积,再除以3计算出原来长方体的长,原来长方体的宽和长相等,用长加上3cm就是原来长方体的高;最后根据长方体的表面积=(长×宽+长×高+宽×高)×2,代入相应数值计算,据此解答。
【详解】原来长方体的长:96÷4÷3=8(cm)
原来长方体的宽:8cm
原来长方体的高:8+3=11(cm)
(8×8+8×11+8×11)×2
=(64+88+88)×2
=240×2
=480(cm2)
因此原来长方体的表面积是480cm2。
12.1
【分析】由题意可知,底面积是100平方厘米的正方体容器,则这个正方体容器的棱长是10厘米,再根据正方体的体积=底面积×高,可求得这个容器的容积,最后根据1L=1000立方厘米转换单位即可解答。
【详解】因为10×10=100(平方厘米),所以正方体的棱长是10厘米。
100×10=1000(立方厘米)
1000立方厘米=1升
所以,最多能装1升水。
13.×
【分析】根据正方体的特征,12条棱都相等,那么拼成的大正方体的每条棱长上至少要放2个同样的小正方体,即至少需要2×2×2=8(个)小正方体。
【详解】如图:
2×2×2=8(个)
至少用8个小正方体就可以拼成一个大正方体。原题说法错误。
故答案为:×
14.×
【分析】正方体的表面积是指它的6个面的总面积;正方体的体积是指正方体所占空间的大小;据此判断即可。
【详解】由分析可知:
表面积和体积是不同的量,无法进行比较。则原题干说法错误。
故答案为:×
15.×
【分析】常见的容积单位有毫升、升,计量比较少的液体,通常用毫升作单位,1瓶可乐的容积差不多是300毫升,1升相当于2瓶矿泉水的容积。据此判断。
【详解】结合生活实际,冰箱容积一般用升作单位,所以原题说法错误。
故答案为:×
16.×
【分析】正方体的表面积是指正方体的6个面的总面积。正方体的体积是指正方体所占空间的大小。因为表面积和体积不是同类量,所以无法进行比较,据此判断。
【详解】正方体的表面积和体积不是同类量,所以无法进行比较。
原题说法错误。
故答案为:×
17.√
【分析】表面积是指物体所有面的面积总和。正方体玻璃鱼缸没有盖,所以鱼缸的只有5个面,制作这5个面至少需要多少平方分米玻璃,就是求这个鱼缸的表面积是多少。这个鱼缸的表面积=棱长×棱长×5,代入数据计算,即可解答。
【详解】由分析得:
6×6×5=180(平方分米)
制作这个鱼缸至少需要180平方分米玻璃。
一个正方体玻璃鱼缸的棱长是6分米,求制作这个鱼缸至少需要多少平方分米玻璃,就是求这个鱼缸的表面积是多少,该说法是正确的。
故答案为:√
18.70;10;1;980;16.4
3;7;0.88;0.008;0.01
【解析】略
19.(1)360
(2)352
【分析】(1)根据长方体的表面积=(长×宽+宽×高+长×高)×2,代入数据计算即可。
(2)由图可知,长方体的底面积是16,高是22cm,根据长方体的体积=底面积×高,代入数据计算即可。
【详解】(1)(12×6+6×6+12×6)×2
=(72+36+72)×2
=(108+72)×2
=180×2
=360()
(2)16×22=352()
20.432立方厘米;396平方厘米
【分析】这个物体的体积等于长6厘米、宽3厘米、高4厘米的长方体的体积加上长12厘米、宽5厘米、高6厘米的长方体的体积,根据长方体的体积=长×宽×高计算;
这个物体的表面积等于长12厘米、宽5厘米、高6厘米的长方体的表面积加上长6厘米、宽3厘米、高4厘米的长方体的侧面积,根据长方体的表面积=(长×宽+宽×高+长×高)×2,长方体的侧面积=(长+宽)×2×高,代入数据计算即可解答。
【详解】6×3×4+12×5×6
=18×4+60×6
=72+360
=432(立方厘米)
(12×5+5×6+12×6)×2+(6+3)×2×4
=(60+30+72)×2+9×2×4
=(90+72)×2+18×4
=162×2+72
=324+72
=396(平方厘米)
21.98厘米
【分析】观察图形可知,捆扎这个包装盒至少需要彩带的长度=2条长+2条宽+4条高+打结用的长度,据此解答。
【详解】15×2+10×2+8×4+16
=30+20+32+16
=98(厘米)
答:一共需要98厘米的彩带。
22.4立方分米
【分析】根据题意,把一些金鱼和鹅卵石完全浸没在装有水的长方体玻璃鱼缸里,水面上升了0.2分米,那么水上升部分的体积就是金鱼和鹅卵石的体积;根据长方体的体积=长×宽×高,代入数据计算求解。
【详解】5×4×0.2
=20×0.2
=4(立方分米)
答:金鱼和鹅卵石的体积一共是4立方分米。
23.(1)28分米;
(2)24平方分米
【分析】(1)计算需要铁丝的长度就是求长方体的棱长之和,长方体的棱长之和=(长+宽+高)×4,把图中数据代入公式计算;
(2)长方体有两个相对的面是正方形,其它四个面都是相同的长方形,计算需要黄绸布的面积就是求长方体四个侧面的面积之和,据此解答。
【详解】(1)(2+2+3)×4
=7×4
=28(分米)
答:她至少用了28分米长的铁丝。
(2)2×3×4
=6×4
=24(平方分米)
答:她至少用了24平方分米的黄绸布。
24.(1)510平方分米
(2)450升
【分析】(1)根据题意,给长方体水池的四周及底部贴上瓷砖,即贴瓷砖的是长方体的下面、前后面、左右面共5个面;根据“长×宽+长×高×2+宽×高×2”求出这5个面的面积之和,即是需要贴瓷砖的面积。
(2)如果要往这个水池里注入5分米深的水,根据长方体的体积=长×宽×高,求出水的体积,然后根据进率“1立方分米=1升”换算单位即可。
【详解】(1)15×6+15×10×2+6×10×2
=90+300+120
=510(平方分米)
答:需要贴瓷砖的面积是510平方分米。
(2)15×6×5
=90×5
=450(立方分米)
450立方分米=450升
答:需要450升水。
25.8厘米
【分析】已知一个长10厘米、宽8厘米的长方体密封盒内水深4厘米,根据长方体的体积=长×宽×高,求出水的体积;
然后将它竖立放置,水的体积不变,但密封盒的底面积变成是(8×5)平方厘米,根据长方体的高=体积÷底面积,即可求出这时水的深度。
【详解】水的体积:
10×8×4=320(立方厘米)
水深:
320÷(8×5)
=320÷40
=8(厘米)
答:这时水深8厘米。
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
中小学教育资源及组卷应用平台
第3单元长方体和正方体素养检测卷-2024-2025学年数学五年级下册人教版
一、选择题
1.下面可以算出正方体体积的公式有( )。
A.棱长×棱长×棱长
B.长×宽×高
C.底面积×高
D.以上都可以
2.如图与4号面相对的面是( )。
A.1 B.2 C.3 D.6
3.一个长方体右面的面积是56cm2,长是7cm,高是6cm。要计算这个长方体的体积,正确的算式是( )。
A.6×7 B.56×6 C.56×7 D.56×6×7
4.如图是一个长方体,与棱h平行的棱一共有( )条。
A.1 B.2 C.3 D.4
5.一个棱长为8的正方体,由若干个棱长为1的小正方体组成,那么这个大正方体含有( )个这样的小正方体。
A.296 B.384 C.328 D.512
6.正方体的棱长扩大2倍,表面积扩大到原来的( )倍,体积扩大到原来的( )倍。括号里依次应填入( )。
A.2;8 B.4;8 C.6;8 D.8;4
二、填空题
7.填一填。
3升40毫升=( )升 8.25时=( )分 5.04平方千米=( )公顷
8.(如图)用彩带包扎一个长40cm、宽20cm、高18cm的长方体礼盒。打结处用了彩带15cm,包装这个礼盒共用彩带( )。
9.如图,墙角堆放一些棱长5cm的正方体,露在外面的面的面积是( )cm2。
10.一个能容纳128L水的长方体桶,高0.64m,它的底面积是( )。
11.一个长方体,如果高减少就变成了一个正方体,这时表面积就减少,原来长方体的表面积是( )。
12.一个底面积是100平方厘米的正方体容器,最多能装( )L水。
三、判断题
13.至少用4个小正方体就可以拼成一个大正方体。( )
14.棱长是9cm的正方体,它的体积大于表面积。( )
15.李师傅家的冰箱容积有220毫升。( )
16.棱长为6cm的正方体表面积和体积相等。( )
17.一个正方体玻璃鱼缸的棱长是6分米,求制作这个鱼缸至少需要多少平方分米玻璃,就是求这个鱼缸的表面积是多少。( )
四、计算题
18.直接写出得数。
0.7×100= 12.5×0.8= 0.25×4= 9.8÷0.01= 3.4+13=
0.36÷0.12= 350÷50= 10-9.12= 0.23= 2×0.1÷2×0.1=
19.按要求计算。
(1)计算长方体的表面积。
(2)计算长方体的体积。
20.如图:求这个物体的体积和表面积。(单位:厘米)
五、解答题
21.妈妈为小明准备了六一儿童节礼物,如图是这个节日礼物的包装盒,它的长、宽、高分别是15厘米、10厘米、8厘米,用彩带把这个包装盒捆上,捆扎处用去彩带16厘米,一共需要多少厘米的彩带?
22.一个无盖的长方体玻璃鱼缸,长5分米,宽4分米,高6分米。在鱼缸里注入适量的水,再往水里放入一些金鱼和鹅卵石(完全浸没),水面上升了0.2分米。金鱼和鹅卵石的体积一共是多少立方分米?
23.元宵节是我国的传统节日,同学们庆元宵,正在制作长方体的灯笼。
(1)小红首先用铁丝制作了一个如图所示的长方体灯笼框架,她至少用了多长的铁丝?
(2)小芳在框架的四个侧面围上黄绸布(上、下面是空的),她至少用了多少平方分米的黄绸布?
24.一个长方体水池从里面量长15分米,宽6分米,高10分米。
(1)如果把这个水池的四周及底部贴上瓷砖,那么需要贴瓷砖的面积是多少?
(2)如果要往这个水池里注入5分米深的水,那么需要多少升水?
25.在一个长10厘米,宽8厘米,高5厘米的密封盒中,测得水深4厘米。然后将它竖立放置,这时水深多少厘米?
中小学教育资源及组卷应用平台
中小学教育资源及组卷应用平台
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
《第3单元长方体和正方体素养检测卷-2024-2025学年数学五年级下册人教版》参考答案
题号 1 2 3 4 5 6
答案 D C C C D B
1.D
【分析】根据,及,逐项分析。
【详解】A.根据正方体的体积公式可知,该选项符合题意。
B.正方体是长、宽、高相等的长方体,所以长×宽×高即棱长×棱长×棱长,该选项符合题意。
C.底面积为棱长×棱长,高等于棱长,乘积仍与棱长×棱长×棱长相等,该选项符合题意。
选项A、B、C都可以算出正方体体积。
故答案为:D
2.C
【分析】据图可知,这是“1-3-2”型正方体展开图,可以把4号面看作下面,则5号面和1号面是左右面,2号面和6号面是前后面,3号面和4号面是上下面,据此解答。
【详解】据图可知,6号面和2号面相对,1号面和5号面相对,4号面和3号面相对。
故答案为:C
3.C
【分析】分析题目,长方体右面的面积=宽×高,根据长方体的体积=长×宽×高可知:长方体的体积=右面的面积×长,据此解答。
【详解】56×7=392(cm3)
一个长方体右面的面积是56cm2,长是7cm,高是6cm。要计算这个长方体的体积,正确的算式是56×7。
故答案为:C
4.C
【分析】长方体有12条棱,相对的四条棱长度相等,按长度可分为三组,每一组有4条棱。
【详解】如图:
与棱h平行的棱分别是AB、CD、EF,一共有3条。
故答案为:C
5.D
【分析】根据正方体的体积=棱长×棱长×棱长,分别求出大、小正方体的体积,再相除即可求出小正方体的个数。
【详解】(8×8×8)÷(1×1×1)
=512÷1
=512(个)
这个大正方体含有512个这样的小正方体。
故答案为:D
6.B
【分析】根据正方体的表面积=棱长×棱长×6,正方体的体积=棱长×棱长×棱长可知,正方体的棱长扩大2倍,表面积扩大到原来的(2×2)倍,体积扩大到原来的(2×2×2)倍,据此解答。
【详解】2×2=4
2×2×2=8
正方体的棱长扩大2倍,表面积扩大到原来的4倍,体积扩大到原来的8倍。
故答案为:B
7. 3.04// 495 504
【分析】根据1升=1000毫升,1时=60分,1平方千米=100公顷,把高级单位的名数换算成低级单位的名数,就乘单位间的进率,把低级单位的名数换算成高级单位的名数,就除以单位间的进率。复名数换单名数,单位相同的不用换,单位不同的先统一单位,再加上之前没换单位部分的数,据此解答。
【详解】
(升)或(升)或(升)
(分)
(公顷)
3升40毫升=3.4(或或)升 8.25时=495分 5.04平方千米=504公顷
8.207cm/207厘米
【分析】观察图形可知,包装这个礼盒至少需要彩带的长度=2条长+2条宽+4条高+打结用的长度,据此解答。
【详解】40×2+20×2+18×4+15
=80+40+72+15
=207(cm)
包装这个礼盒共用彩带207cm。
9.225
【分析】分析题目,露在外面的面的面积=露在外面的面的个数×一个面的面积,据此先数出露在外面的一共有几个面,再根据棱长×棱长求出一个面的面积,最后求出它们的乘积即可。
【详解】9×(5×5)
=9×25
=225(cm2)
墙角堆放一些棱长5cm的正方体,露在外面的面的面积是225cm2。
10.0.2 m2
【分析】1L=1dm3,1m3=1000dm3;根据长方体的体积(容积)公式:v=sh,那么s=v÷h,用水的体积除以长方体水桶的高即可解答。
【详解】128L=128dm3=0.128m3
0.128÷0.64=0.2()
所以,它的底面积是0.2 。
11.480
【分析】一个长方体如果高减少3cm就变成一个正方体,说明原来长方体的长和宽相等;高减少3cm,表面积就减少96cm2,则减少的表面积就是4个相同的长方形的面积之和,用96除以4求出一个面的面积,再除以3计算出原来长方体的长,原来长方体的宽和长相等,用长加上3cm就是原来长方体的高;最后根据长方体的表面积=(长×宽+长×高+宽×高)×2,代入相应数值计算,据此解答。
【详解】原来长方体的长:96÷4÷3=8(cm)
原来长方体的宽:8cm
原来长方体的高:8+3=11(cm)
(8×8+8×11+8×11)×2
=(64+88+88)×2
=240×2
=480(cm2)
因此原来长方体的表面积是480cm2。
12.1
【分析】由题意可知,底面积是100平方厘米的正方体容器,则这个正方体容器的棱长是10厘米,再根据正方体的体积=底面积×高,可求得这个容器的容积,最后根据1L=1000立方厘米转换单位即可解答。
【详解】因为10×10=100(平方厘米),所以正方体的棱长是10厘米。
100×10=1000(立方厘米)
1000立方厘米=1升
所以,最多能装1升水。
13.×
【分析】根据正方体的特征,12条棱都相等,那么拼成的大正方体的每条棱长上至少要放2个同样的小正方体,即至少需要2×2×2=8(个)小正方体。
【详解】如图:
2×2×2=8(个)
至少用8个小正方体就可以拼成一个大正方体。原题说法错误。
故答案为:×
14.×
【分析】正方体的表面积是指它的6个面的总面积;正方体的体积是指正方体所占空间的大小;据此判断即可。
【详解】由分析可知:
表面积和体积是不同的量,无法进行比较。则原题干说法错误。
故答案为:×
15.×
【分析】常见的容积单位有毫升、升,计量比较少的液体,通常用毫升作单位,1瓶可乐的容积差不多是300毫升,1升相当于2瓶矿泉水的容积。据此判断。
【详解】结合生活实际,冰箱容积一般用升作单位,所以原题说法错误。
故答案为:×
16.×
【分析】正方体的表面积是指正方体的6个面的总面积。正方体的体积是指正方体所占空间的大小。因为表面积和体积不是同类量,所以无法进行比较,据此判断。
【详解】正方体的表面积和体积不是同类量,所以无法进行比较。
原题说法错误。
故答案为:×
17.√
【分析】表面积是指物体所有面的面积总和。正方体玻璃鱼缸没有盖,所以鱼缸的只有5个面,制作这5个面至少需要多少平方分米玻璃,就是求这个鱼缸的表面积是多少。这个鱼缸的表面积=棱长×棱长×5,代入数据计算,即可解答。
【详解】由分析得:
6×6×5=180(平方分米)
制作这个鱼缸至少需要180平方分米玻璃。
一个正方体玻璃鱼缸的棱长是6分米,求制作这个鱼缸至少需要多少平方分米玻璃,就是求这个鱼缸的表面积是多少,该说法是正确的。
故答案为:√
18.70;10;1;980;16.4
3;7;0.88;0.008;0.01
【解析】略
19.(1)360
(2)352
【分析】(1)根据长方体的表面积=(长×宽+宽×高+长×高)×2,代入数据计算即可。
(2)由图可知,长方体的底面积是16,高是22cm,根据长方体的体积=底面积×高,代入数据计算即可。
【详解】(1)(12×6+6×6+12×6)×2
=(72+36+72)×2
=(108+72)×2
=180×2
=360()
(2)16×22=352()
20.432立方厘米;396平方厘米
【分析】这个物体的体积等于长6厘米、宽3厘米、高4厘米的长方体的体积加上长12厘米、宽5厘米、高6厘米的长方体的体积,根据长方体的体积=长×宽×高计算;
这个物体的表面积等于长12厘米、宽5厘米、高6厘米的长方体的表面积加上长6厘米、宽3厘米、高4厘米的长方体的侧面积,根据长方体的表面积=(长×宽+宽×高+长×高)×2,长方体的侧面积=(长+宽)×2×高,代入数据计算即可解答。
【详解】6×3×4+12×5×6
=18×4+60×6
=72+360
=432(立方厘米)
(12×5+5×6+12×6)×2+(6+3)×2×4
=(60+30+72)×2+9×2×4
=(90+72)×2+18×4
=162×2+72
=324+72
=396(平方厘米)
21.98厘米
【分析】观察图形可知,捆扎这个包装盒至少需要彩带的长度=2条长+2条宽+4条高+打结用的长度,据此解答。
【详解】15×2+10×2+8×4+16
=30+20+32+16
=98(厘米)
答:一共需要98厘米的彩带。
22.4立方分米
【分析】根据题意,把一些金鱼和鹅卵石完全浸没在装有水的长方体玻璃鱼缸里,水面上升了0.2分米,那么水上升部分的体积就是金鱼和鹅卵石的体积;根据长方体的体积=长×宽×高,代入数据计算求解。
【详解】5×4×0.2
=20×0.2
=4(立方分米)
答:金鱼和鹅卵石的体积一共是4立方分米。
23.(1)28分米;
(2)24平方分米
【分析】(1)计算需要铁丝的长度就是求长方体的棱长之和,长方体的棱长之和=(长+宽+高)×4,把图中数据代入公式计算;
(2)长方体有两个相对的面是正方形,其它四个面都是相同的长方形,计算需要黄绸布的面积就是求长方体四个侧面的面积之和,据此解答。
【详解】(1)(2+2+3)×4
=7×4
=28(分米)
答:她至少用了28分米长的铁丝。
(2)2×3×4
=6×4
=24(平方分米)
答:她至少用了24平方分米的黄绸布。
24.(1)510平方分米
(2)450升
【分析】(1)根据题意,给长方体水池的四周及底部贴上瓷砖,即贴瓷砖的是长方体的下面、前后面、左右面共5个面;根据“长×宽+长×高×2+宽×高×2”求出这5个面的面积之和,即是需要贴瓷砖的面积。
(2)如果要往这个水池里注入5分米深的水,根据长方体的体积=长×宽×高,求出水的体积,然后根据进率“1立方分米=1升”换算单位即可。
【详解】(1)15×6+15×10×2+6×10×2
=90+300+120
=510(平方分米)
答:需要贴瓷砖的面积是510平方分米。
(2)15×6×5
=90×5
=450(立方分米)
450立方分米=450升
答:需要450升水。
25.8厘米
【分析】已知一个长10厘米、宽8厘米的长方体密封盒内水深4厘米,根据长方体的体积=长×宽×高,求出水的体积;
然后将它竖立放置,水的体积不变,但密封盒的底面积变成是(8×5)平方厘米,根据长方体的高=体积÷底面积,即可求出这时水的深度。
【详解】水的体积:
10×8×4=320(立方厘米)
水深:
320÷(8×5)
=320÷40
=8(厘米)
答:这时水深8厘米。
21世纪教育网(www.21cnjy.com)
21世纪教育网(www.21cnjy.com)
