10.3 一次函数的性质 课件

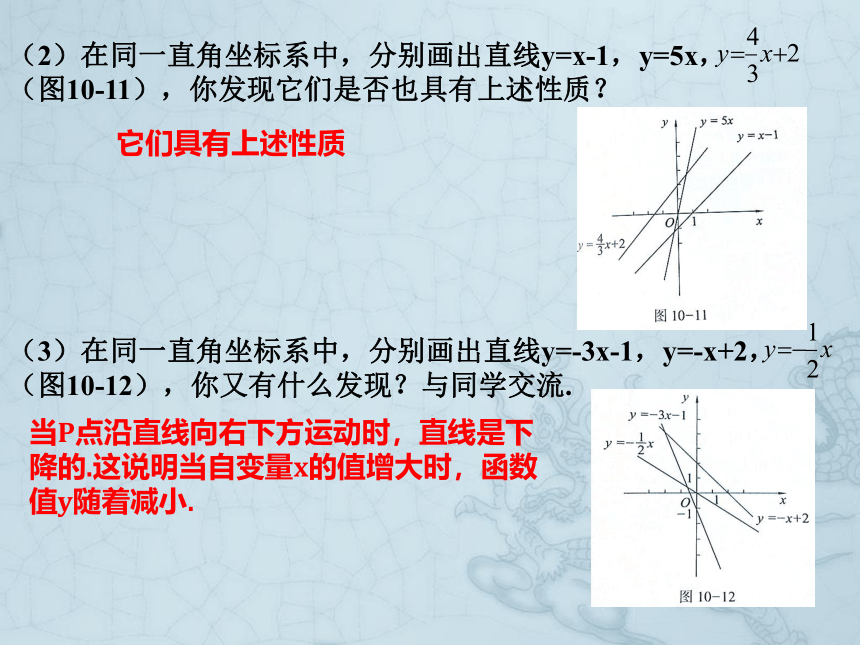
课件10张PPT。10.3 一次函数的性质学习目标1.结合函数图象，理解正比例函数与一次函数的性质.2.加强图象与函数表达式，即“数”与“形”的联系.相关知识链接1.一次函数：形如 （k≠0）的函数叫做x的一次函数，其中k与b是常数.特别地，当b=0时，一次函数y=kx也叫做正比例函数，k叫做比例系数.y=k x＋b2.一次函数y=k x＋b（k≠0），当b≠0时，它的图象与x轴的交点坐标是 ，与y轴的交点坐标是 .（ ，0）（0，b）观察与思考（1）如图10-9，设P(x，y)是直线y=2x+4上的一个动点，当点P沿直线向右上方运动时，点的横坐标x与纵坐标y发生怎样的变化？这说明一次函数y=2x+4当自变量x的值增大时，函数值y有怎样的变化？当P沿直线向右上方运动时，直线是上升的.这说明当自变量x的值增大时，函数y的值也随着增大.（2）在同一直角坐标系中，分别画出直线y=x-1，y=5x， （图10-11），你发现它们是否也具有上述性质？它们具有上述性质（3）在同一直角坐标系中，分别画出直线y=-3x-1，y=-x+2， （图10-12），你又有什么发现？与同学交流.当P点沿直线向右下方运动时，直线是下降的.这说明当自变量x的值增大时，函数值y随着减小.（4）比较（2）（3）中你的发现，你能总结出一次函数y=k x＋b当自变量x增加时，函数值y的变化吗？一般地，对于一次函数y=k x＋b，当k>0时，y随着x的增大而增大；当k<0时，y随着x的增大而减小.例1已知一次函数y=（m+2）x+ ，当m为何值时，y随着x的增大而减小？解：根据一次函数的性质，当m+2<0时，y随着x的增大而减小.解不等式m+2<0，得m<-2.所以，当m<-2时，y随着x的增大而减小.例2已知一次函数y=kx-k ，且y随着x的增大而增大，试探索它的图象经过哪几个象限.解：因为一次函数y=kx-k的y随x的增大而增大，所以k>0.又因为x=0时，y=-k<0，所以直线y=kx-k与y轴的交点（0，-k）在y轴的负半轴，且当y=0时，x=1，故直线y=kx-k与x轴的交点为（1,0）.它的图象大致如图10-13所示，这条直线经过第一、三、四象限.练习作业布置课本146页 习题10.3
第1、3、4题.