浙江中考复习——集训精选题（二）

中小学教育资源及组卷应用平台
浙江中考复习——集训精选题（二）
一、选择题
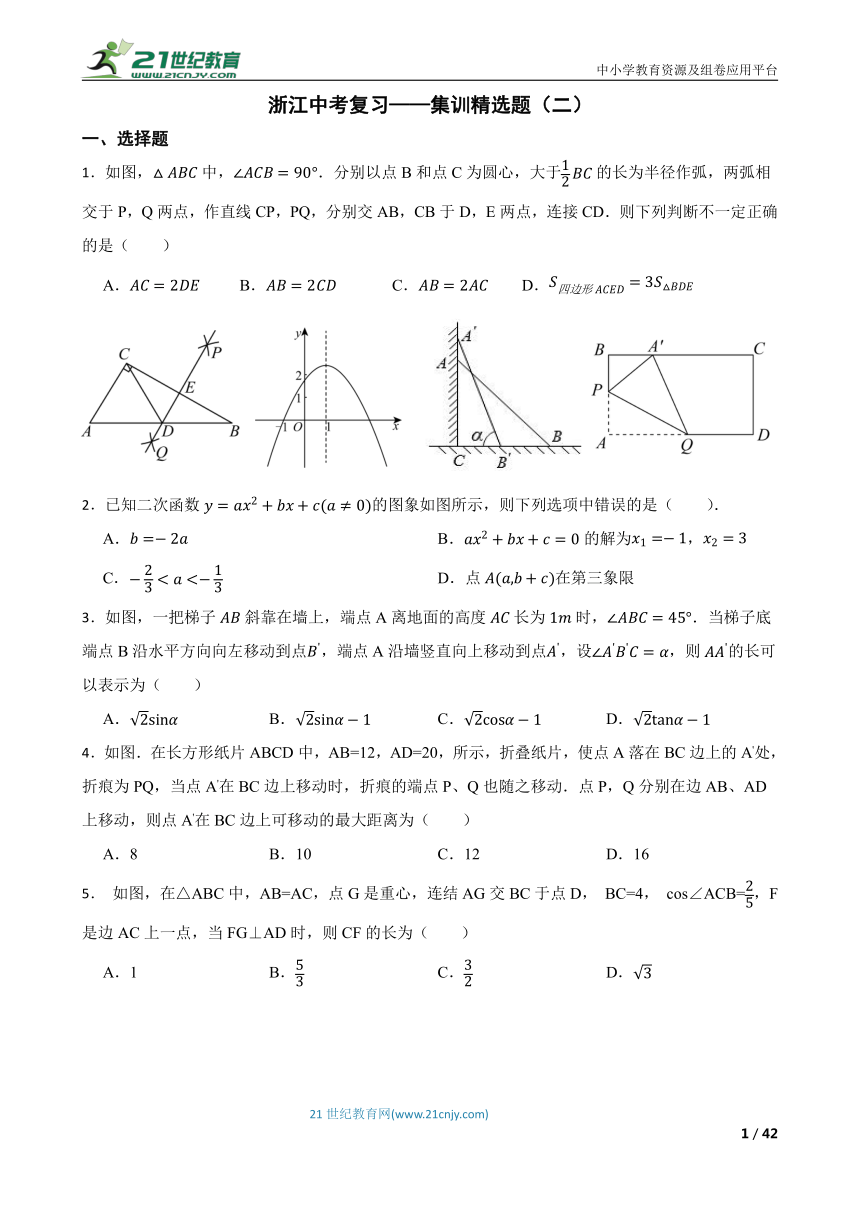
1．如图，中，．分别以点B和点C为圆心，大于的长为半径作弧，两弧相交于P，Q两点，作直线CP，PQ，分别交AB，CB于D，E两点，连接CD．则下列判断不一定正确的是（　　）
A． B． C． D．
2．已知二次函数的图象如图所示，则下列选项中错误的是（　　）．
A． B．的解为，
C． D．点在第三象限
3．如图，一把梯子斜靠在墙上，端点A离地面的高度长为时，．当梯子底端点B沿水平方向向左移动到点，端点A沿墙竖直向上移动到点，设，则的长可以表示为（　　）
A． B． C． D．
4．如图．在长方形纸片ABCD中，AB=12，AD=20，所示，折叠纸片，使点A落在BC边上的A'处，折痕为PQ，当点A'在BC边上移动时，折痕的端点P、Q也随之移动．点P，Q分别在边AB、AD上移动，则点A'在BC边上可移动的最大距离为（　　）
A．8 B．10 C．12 D．16
5． 如图，在△ABC中，AB=AC，点G是重心，连结AG交BC于点D， BC=4， cos∠ACB=，F是边AC上一点，当FG⊥AD时，则CF的长为（　　）
A．1 B． C． D．
6．如图，已知CD⊥x轴，垂足为D，CO，CD分别交反比例函数y=的图象于点A，B.若OA=AC，则△OBC的面积为（　　）
A．4 B．6 C．8 D．10
二、填空题（本大题有6小题，每小题3分，共18分）
7．如图，在△ABC中，AB＝AC＝，BC＝2，以点A为圆心作圆弧，与BC相切于点D，且分别交边AB，AC于点EF，则扇形AEF的面积为 　 　．（结果保留π）
8．如图，已知点 A ，B分别在反比例函数与的图象上，且．若，则的面积为　 　．
9．如图，在四边形ABCD中，AD//BC，∠ABC=90°，点E在AB的延长线上，DE分别交BC，AC于点F，G.若AB=5，AE=AD=8，EF=DG，则BC=　 　.
10．如图1是某一遮阳蓬支架从闭合到完全展开的一个过程，当遮阳蓬支架完全闭合时，支架的若干支杆可看作共线．图2是遮阳蓬支架完全展开时的一个示意图，支杆MN固定在垂直于地面的墙壁上，支杆CE与水平地面平行，且G，F，B三点共线，在支架展开过程中四边形ABCD始终是平行四边形．
（1）若遮阳蓬完全展开时，CE长2米，在与水平地面呈60°的太阳光照射下，CE在地面的影子有　 　米（影子完全落在地面）
（2）长支杆与短支杆的长度比（即CE与AD的长度比）是　 　．
三、一次函数与反比例函数
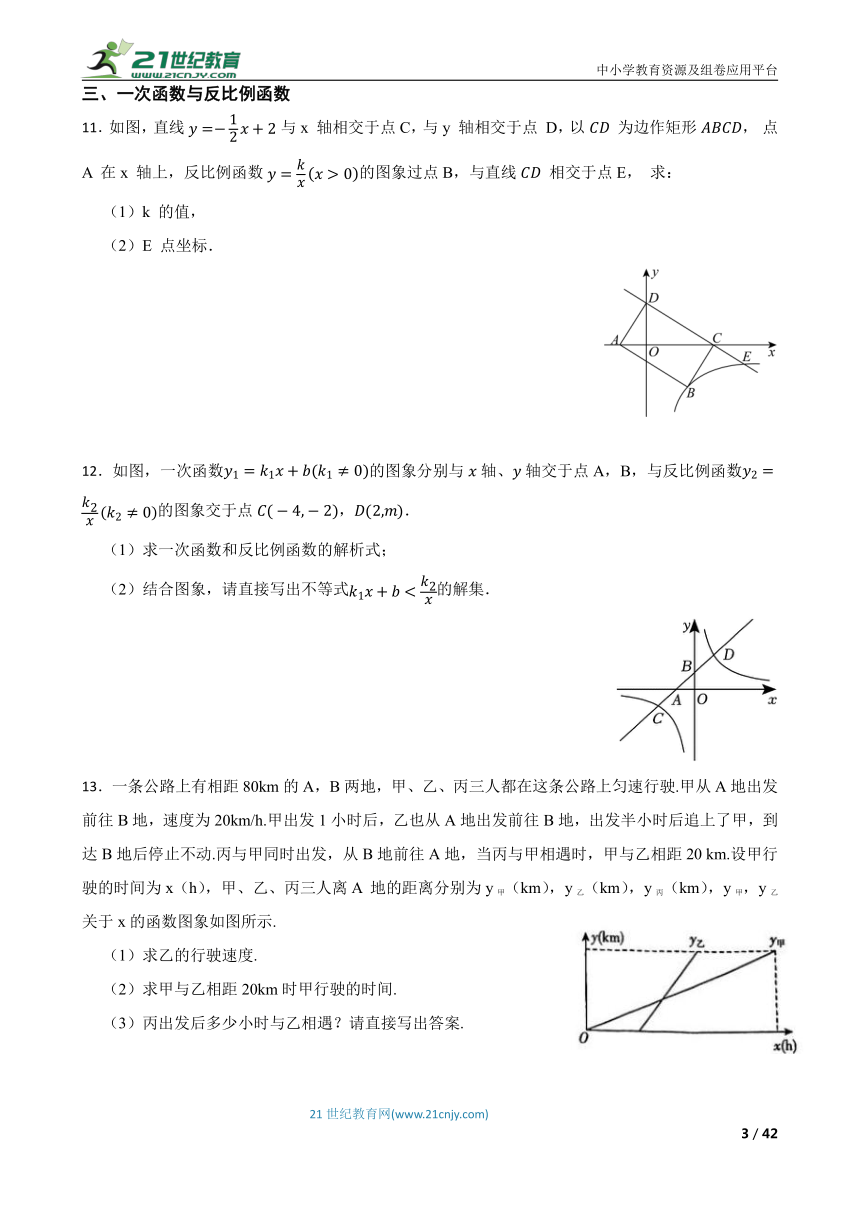
11．如图，直线与x 轴相交于点C，与y 轴相交于点 D，以 为边作矩形， 点 A 在x 轴上，反比例函数的图象过点B，与直线 相交于点E， 求：
（1）k 的值，
（2）E 点坐标．
12．如图，一次函数的图象分别与轴、轴交于点A，B，与反比例函数的图象交于点，．
（1）求一次函数和反比例函数的解析式；
（2）结合图象，请直接写出不等式的解集．
13．一条公路上有相距80km的A，B两地，甲、乙、丙三人都在这条公路上匀速行驶.甲从A地出发前往B地，速度为20km/h.甲出发1小时后，乙也从A地出发前往B地，出发半小时后追上了甲，到达B地后停止不动.丙与甲同时出发，从B地前往A地，当丙与甲相遇时，甲与乙相距20 km.设甲行驶的时间为x（h），甲、乙、丙三人离A 地的距离分别为y甲（km），y乙（km），y丙（km），y甲，y乙关于x的函数图象如图所示.
（1）求乙的行驶速度.
（2）求甲与乙相距20km时甲行驶的时间.
（3）丙出发后多少小时与乙相遇？请直接写出答案.
四、解直角三角形
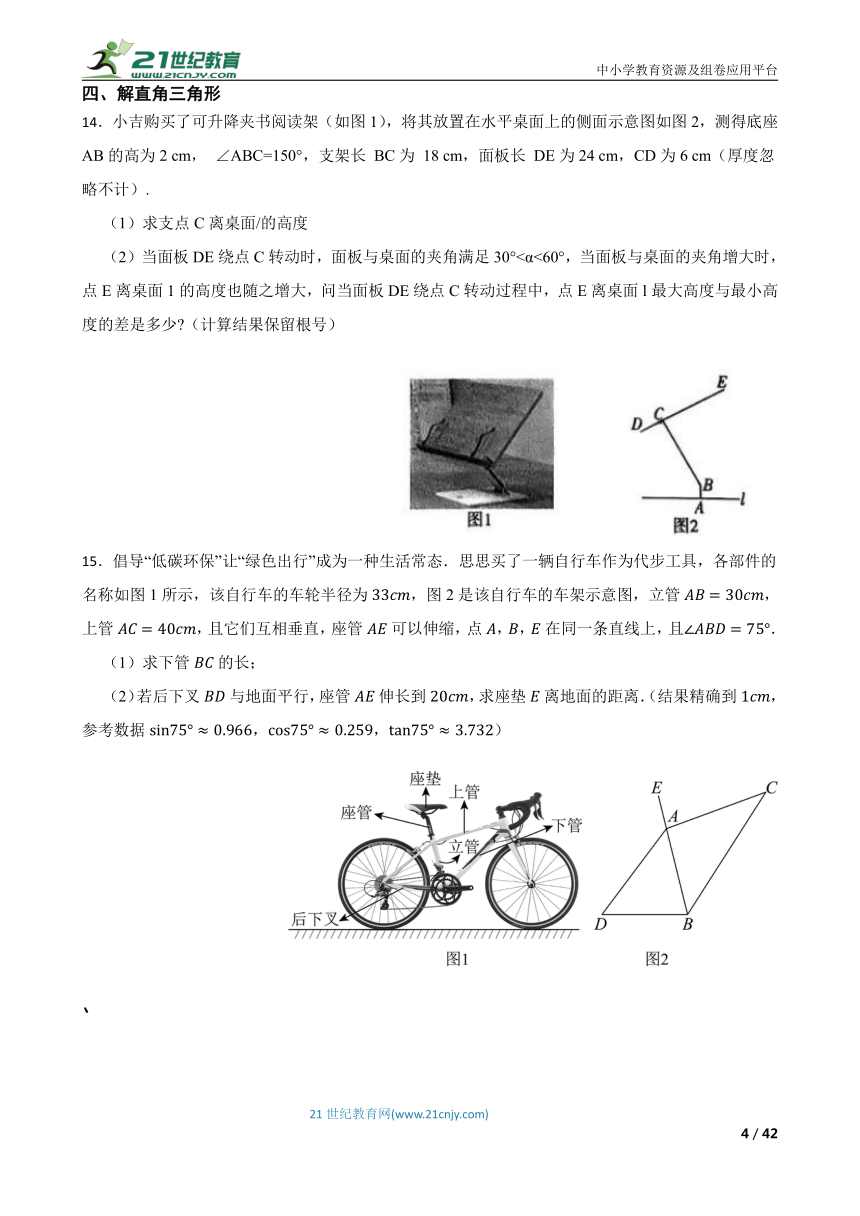
14．小吉购买了可升降夹书阅读架（如图1），将其放置在水平桌面上的侧面示意图如图2，测得底座AB的高为2 cm， ∠ABC=150°，支架长 BC为 18 cm，面板长 DE为24 cm，CD为6 cm（厚度忽略不计）.
（1）求支点C离桌面/的高度
（2）当面板DE绕点C转动时，面板与桌面的夹角满足30°<α<60°，当面板与桌面的夹角增大时，点E离桌面1的高度也随之增大，问当面板DE绕点C转动过程中，点E离桌面l最大高度与最小高度的差是多少 （计算结果保留根号）
15．倡导“低碳环保”让“绿色出行”成为一种生活常态．思思买了一辆自行车作为代步工具，各部件的名称如图1所示，该自行车的车轮半径为，图2是该自行车的车架示意图，立管，上管，且它们互相垂直，座管可以伸缩，点，，在同一条直线上，且．
（1）求下管的长；
（2）若后下叉与地面平行，座管伸长到，求座垫离地面的距离．（结果精确到，参考数据，，）
、
五、函数实际应用
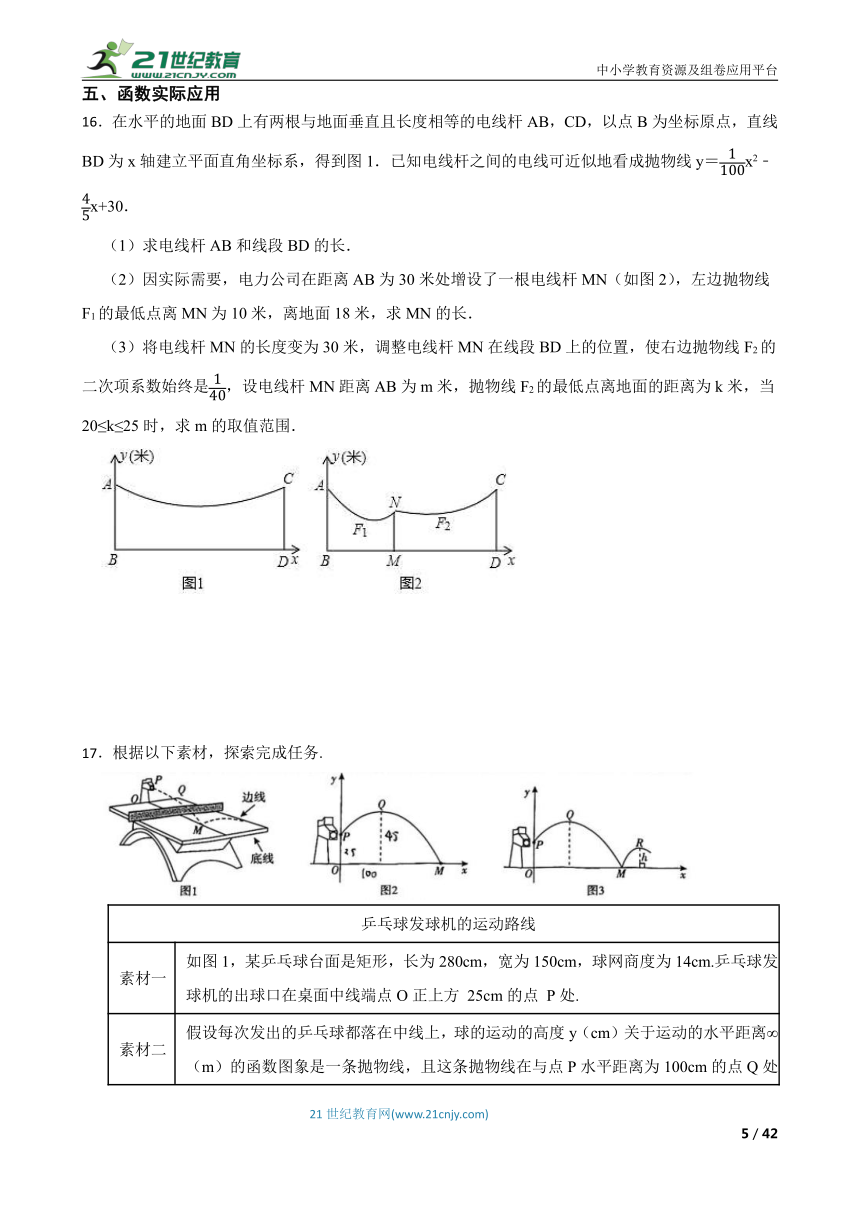
16．在水平的地面BD上有两根与地面垂直且长度相等的电线杆AB，CD，以点B为坐标原点，直线BD为x轴建立平面直角坐标系，得到图1．已知电线杆之间的电线可近似地看成抛物线y＝x2﹣x+30．
（1）求电线杆AB和线段BD的长．
（2）因实际需要，电力公司在距离AB为30米处增设了一根电线杆MN（如图2），左边抛物线F1的最低点离MN为10米，离地面18米，求MN的长．
（3）将电线杆MN的长度变为30米，调整电线杆MN在线段BD上的位置，使右边抛物线F2的二次项系数始终是，设电线杆MN距离AB为m米，抛物线F2的最低点离地面的距离为k米，当20≤k≤25时，求m的取值范围．
17．根据以下素材，探索完成任务.
乒乓球发球机的运动路线
素材一 如图1，某乒乓球台面是矩形，长为280cm，宽为150cm，球网商度为14cm.乒乓球发球机的出球口在桌面中线端点O正上方 25cm的点 P处.
素材二 假设每次发出的乒乓球都落在中线上，球的运动的高度y（cm）关于运动的水平距离∞（m）的函数图象是一条抛物线，且这条抛物线在与点P水平距离为100cm的点Q处达到最高高度，此时距桌面的高度为45cm，乒乓球落在桌面的点M处.以O为原点，桌面中线所在直线为∞轴，建立如图2所示的平面直角坐标系。
素材三 如图3，若乒乓球落在桌面上弹起后，在与点O的水平距离为300cm的点R处达到最高，设弹起后球达到最高时距离桌面的高度为h（cm）.
问题解决
任务一 研究乒乓球的 （1）求出从发球机发球后到落在桌面前，乒乓球运动轨迹的函数表达式（不要求飞行轨迹写出自变量的取值范围）.
任务二 击球点的确定 （2）当h=20时，运动员小亮想在点R处把球沿直线擦网击打到点O，他能不能实现？请说明理由。
任务三 击球点的距离 （3）若h=40，且弹起后球飞行的高度在离桌面30cm至50cm时，小亮可以获得最佳击球效果，求击球点与发球机水平距离的取值范围。
六、二次函数
18．已知二次函数．
（1）若函数图象经过点．
①求该二次函数的表达式．
②若将平面内一点向左平移个单位，则与图象上的点重合；若将点A向右平移个单位，则与图象上的点重合，求的值．
（2）设点，是该函数图象上的两点，若，求证：．
19．在直角坐标系中，设函数（m，n是实数）．
（1）当时，若该函数的图象经过点，求函数的表达式．
（2）若，且当时，y随x的增大而减小，求m的取值范围．
（3）若该函数的图象经过，两点（a，b是实数）．当时，求证：．
20．如图，二次函数的图象过，，三点，点是二次函数图象上一点，点的横坐标是，直线与轴交于点，且．
（1）求二次函数的表达式；
（2）过点，作直线于点，作轴于点，并交于点．
①当时，求的长；
②是否存在点，使最大？若存在，求出点坐标，若不存在，请说明理由．
七、平面几何
21．如图，在中，，垂足为D，E为线段上一点，且，过E作交于F．
（1）求证：．
（2）求的长．
22．在中，D，E分别是，的中点，延长至点F，使得，连接．
（1）求证：四边形是平行四边形．
（2）于点G，连接，若G是的中点，，，
①求的长．
②求平行四边形的周长．
23．如图，在中，，D，E为上的动点，且，P为的中点．
（1）若，求的长．
（2）在线段的运动过程中，的长由2到，求这一变化过程中，点 P运动的路程．
（3）连结，求的最小值．
八、园几何综合体
24．如图，为的直径，是圆上一点，是的中点，于点，延长至点，连接，．
（1）求证：是的切线；
（2）若点是上的一点，连接、，，．
①求的值；
②若为的角平分线，求的长．
25．如图，内接于，直径交边于点，过点作于点，交于点，连接．
（1）求证：．
（2）若．
①当是等腰三角形时，求的度数．
②若，求的值．
26．如图，为的直径，弦于，为弦上一点，且，射线与射线相交与点.
（1）求证：为的中点.
（2）①若，求的值.
②当为直角三角形时，求的正切值.
答案解析部分
1．【答案】C
【解析】【解答】解：由做图可知垂直平分线段，
得，，
，
，
，
，
是的中位线，，
故选项B正确，不符合题意；
，
故选项A正确，不符合题意；
，，
，，
，
，
故选项D正确，不符合题意；
只有当时，，
故选项C错误，符合题意．
故选：C．
【分析】
由尺规作图的过程知，PQ垂直平分BC，则CD为直角三角形ABC斜边AB上的中线，DE为中位线，再分别对照它们的性质即可判断．
2．【答案】D
【解析】【解答】解：A、由图象可得：对称轴，即，即A选项正确，不符合题意；
B、由函数图象可知：的解为，另一个解为：，即B选项正确，不符合题意；
C、由函数图象可知：且，则有；又当时，，即，即，即C选项正确，不符合题意；
D、由意义可知：，则，又，则，可得点在第二象限，故D选项错误，符合题意．
故选D．
【分析】
观察图象知，抛物线的对称轴为直线，则；若抛物线上任意两点的纵坐标相等，则其横坐标和的一半等于对称轴对应的数字，可知的对称点为；由于抛物线交轴于点，观察图象知，，可利用抛物线与轴的交点坐标确定出的取值范围；由于的取值范围可以确定，则的大体位置也可确定．
3．【答案】B
【解析】【解答】解：由题意可知，，
∵，
∴，故，
∵，
∴，
则：，
故选：B．
【分析】本题考查锐角三角函数.根据正弦的定义可得：，据此可求出，再利用正弦的定义可得：，利用线段的运算可得：，代入数据可求出答案.
4．【答案】A
【解析】【解答】解：①在长方形纸片ABCD中，AB=12，AD=20，
∴BC=AD=20，
当p与B重合时，BA'=BA=12，
CA'=BC-BA'=20-12=8，
②当Q与D重合时，
由折叠得A'D=AD=20，
由勾股定理，得
CA'==16，
CA'最远是16，CA'最近是8，点A'在BC边上可移动的最大距离为16-8=8，
故选：A．
【分析】 本题考查矩形的性质，翻折的性质，勾股定理.利用长方形的性质可得BC=AD=20，分两种情况：当p与B重合时；当Q与D重合时；利用折叠的性质可得：BA'=BA=12，或A'D=AD=20，利用线段的运算，勾股定理可求出A'C，进而求出点A'在BC边上可移动的最大距离．
5．【答案】B
【解析】【解答】解：∵ 在△ABC中，点G是重心，连结AG交BC于点D， BC=4，
∴AD为中线，CD=BC=2，AG：GD=2：1.
∵AB=AC，
∴AD⊥BC，
∴cos∠ACB=，
∵ cos∠ACB=，
∴=，
∴=，解得AC=5，
当FG⊥AD时， GF//CD，
∴AG：GD=AF：FC，
∴AF：FC=2：1，
∴CF=AC=.
故答案为：B.
【分析】先利用三角形重心的意义，说明AD为中线，并求出CD，得出AG：GD=2：1，再利用余弦，求得AC，然后说明GF//CD，列出比例式，说明AF：FC=2：1，就可求出FC.
6．【答案】B
【解析】【解答】解：设A（a，)，则C（2a，），
∵CD⊥x轴，垂足为D，CO，CD分别交反比例函数y=的图象于点A，B，OA=AC，
∴B（2a，)，D（2a，0），
∴.
∴.
∴.
故答案为：B.
【分析】设A（a，)，可用a分别表示出B，C，D的坐标，再求出△BOD，△COD的面积，相减可得△COB的面积.
7．【答案】
【解析】【解答】解：∵AB=AC=，BC=2，
∴AB2+AC2=BC2，
∴△ABC是等腰直角三角形，
∴∠BAC=90°，
连接AD，则AD=BC=1，
则S扇形AEF=．
故答案为：．
【分析】
求扇形面积可先示扇形的中心角，可借助已知条件结合勾股定理的逆定理判定三角形ABC是等腰直角三角形，从而得出中心角是45度，再利用等腰三角形三线合一的性质作底边上的高，从而计算出扇形的半径即可．
8．【答案】
9．【答案】
【解析】【解答】解：∵AB=5，AE=AD=8，
∴BE=AE-AB=3，
∵AD//BC，∠ABC=90°，
∴∠DAE=∠FBE=90°，
∴DE=.
∴∠ADE=∠AED =(180°-∠DAE)=45°，
∴∠BFE=∠ADE=45°，
∴BF=BE=3，
∴EF=.
∴DG=EF=3.
∴FG=DE-DG-EF=2.
∵AD//BC，
∴△ADG∽△CFG.
∴CF：AD=FG：DG，
∴CF：8=2：3，解得CF=.
∴BC=BF+CF=3+=.
故答案为：.
【分析】先利用线段差求出BE，再利用勾股定理求得DE，EF，然后求出FG，再证明△ADG∽△CFG，列出关于CF的比例式，求出CF，再根据BC=BF+CF，求出BC.
10．【答案】2米；2：1
【解析】【解答】解：（1）过C作与水平地面呈60°的直线KC交MN的延长线于K，分别过K、E作KS//CE，ES//CK
∴四边形CESK是平行四边形
∴KS=CE=2，即CE在地面上影子的长为2米；
（2）由题意可知：支杆的竖直长度都一样，且竖直的支点为长支杆的中点，即G为OM、B为OC的中点
当遮阳棚完全闭合后，每根杆的长度都一样，即AD的长度为长支杆的一半
∵CE为长支杆的长度，AD为短支杆的长度．
∴CE：AD=2：1．
【分析】本题考查平行四边形的判定与性质、折叠的性质.
（1） 过C作与水平地面呈60°的直线KC交MN的延长线于K，分别过K、E作KS//CE，ES//CK，利用平行四边形的判定定理可证明四边形CESK是平行四边形，再根据平行四边形的性质可得： KS=CE=2， 据此可求出答案；
（2）由题意可知：支杆的竖直长度都一样，且竖直的支点为长支杆的中点，即G为OM、B为OC的中点，进而可得： 当遮阳棚完全闭合后，每根杆的长度都一样，即AD的长度为长支杆的一半，再根据 CE为长支杆的长度，AD为短支杆的长度． 据此可求出答案.
11．【答案】（1）解：根据题意可知CD所在的直线与AD所在的直线互相垂直，CD所在的直线为 ，
∴可设AD所在的直线为y=2x+b，
∵ 直线与x 轴相交于点C，与y 轴相交于点 D，
∴令x=0，则y=2，
令y=0，则x=4，
∴C（4，0），D（0，2），
∴AD所在的直线为y=2x+2，
∴A（-1，0），
∴在Rt△COD中，CD==，
在Rt△AOD中，AD==，
过点作轴于点M，如图所示：
∵AD∥BC，
∴∠ADO=∠CBM
∵∠AOD=∠COB=90°，AD=BC，
∴△AOD≌△CMB（AAS），
∴BM=OD，CM=AO，
∴OM=OC-CM=3，
∴B（3，-2），
将B代入 反比例函数 ，得：-2=，
∴k=-6
（2）解：根据题意可知点E为 直线与反比例函数的图象的交点，
由（1）可知：反比例函数的解析式为y=（x＞0），
∴将两个函数联立方程组，得：，
解得：（不符合题意，舍去）或
∴
【解析】【分析】（1）根据根据题意可知CD所在的直线与AD所在的直线互相垂直，可设AD所在的直线为y=2x+b，一次函数解析式可得点的坐标，即可求出直线AD的解析式，进而求出点A的坐标，根据勾股定理可得、AD的长，作轴，根据平行线的性质，全等三角形的判定和性质可得△AOD≌△CMB，即可得点的坐标，由此即可求解；
（2）将直线与反比例函数y=联立方程组，求二元一次方程组的解即可．
（1）解：在一次函数中，令，则；令，则；
∴，则，
在中，，
∵四边形是矩形，
∴，，
∴，
∴，且，
∴，
∴，
∴，
∴，，
∴，
∴，
∵，
∴，
如图所示，过点作轴于点，
∴，
∴，
∴，，
∴，即，
∴，
∴反比例函数中；
（2）解：由（1）可得反比例函数，
∴联立方程组得，，
解得，或，
∴．
12．【答案】（1）解：一次函数的图象与反比例函数的图象的相交于点、，
，
，，
反比例函数解析式为，，
把点、的坐标代入得，
解得，
一次函数的表达式为
（2）解：由图象可知，当或时，．
【解析】【分析】 本题反比例函数与一次函数的交点问题，考查待定系数法求函数解析式，反比例函数图象上点的坐标特征，函数与不等式的关系.（1）根据的图象的相交于点、，可得，据此可求出和m的值，据此可得反比例函数解析式为，，把点、的坐标代入可列出方程组，解方程组可求出的值，求出一次函数的表达式；
（2）观察函数图象，找出一次函数图象在反比例函数图象下方的的取值范围为或，据此可写出不等式的解集．
13．【答案】（1）解：乙的速度为20×(1+0.5)÷0.5=60（km/h）.
（2）解：∵甲的速度为20km/h，乙的速度为60km/h，
∴y甲=20x，y乙=60（x-1)，
当甲在乙前面20km时，
20x-60(x-1)=20，
解得x=1，
当乙在甲前面20km时，
60(x-1)-20x=20，
解得x=2，
综上所述，甲与乙相距20km时甲行驶的时间为1h或2h．
（3）解：丙与甲同时出发，从B地前往A地，当丙与甲相遇时，甲与乙相距20km，
∴甲与乙相距20km时，甲和丙行驶时间相等，
∴乙与甲相遇时间为1h或2h，
在y甲=20x中，
当x=1时，y甲=20，
当x=2时，y甲=40，
∴y丙过（1，20）或（2，40），
设y丙=kx+b，
当y丙过（1，20）时，
，
解得；
当y丙过（2，40）时，
，
解得；
∴或.
当丙与乙相遇时，
或，
解得或.
【解析】【分析】（1）根据甲的速度乘以甲出发1小时后，乙用半小时追上，可求出乙的速度；
（2）根据甲、乙的速度，分别求得甲、乙的运动的函数表达式，再分“甲在乙前面20km”、“乙在甲前面20km”两种情况，分别求出所需的时间；
（3）分y丙过（1，20）或（2，40）两种情况，分别求出y丙，当丙与乙相遇时，分别求出x即可.
14．【答案】（1）解：如图，过点C作CF⊥l于点F，过点B作BM⊥CF于点M，
∴∠CFA=∠BMC＝∠BMF=∠BAF=90°，
∴四边形ABMF是矩形，
∴∠ABM=90°，MF=AB=2，
∵∠ABC=150°，
∴∠MBC=∠ABC-∠ABM=60°，
∵BC=18，
∴CM=BCsin60°=9，
∴CF=CM+MF=2+9，
即支点C离桌面l的高度为2+9cm.

（2）解：如图，过点C作CN//l，过E作EH⊥CN于点H，
∴∠EHC=90，
∵DE=24，CD=2，
∴CE=DE-CD=18，
当∠ECH=30°时，
EH=CEsin30°=9；
当∠ECH=60°时，EH=CEsin60°=9；
∴当面板DE绕点C转动过程中，E离桌面1最大高度与最小 高度的差是 9-9cm.
【解析】【分析】(1)先证明四边形ABMF是矩形，根据矩形的性质，可得∠ABM=90°，MF=AB=2，再利用角的和差求出∠MBC，然后利用正弦求出CM，再利用线段的和差求出CF即为支点C离桌面l的高度；
（2）分“∠ECH=30°”、“∠ECH=60°”两种情况，分别求出CH，再求出E离桌面1最大高度与最小 高度的差.
15．【答案】（1）解：根据题意可知：∠CAB=90°，
在△ABC中，AB=30cm，AC=40cm，
根据勾股定理可得：BC==50cm，
答：下管的长为.
（2）解：过点作，垂足为，如图所示：
，，
，
∵，，
∴sin∠ABD=，
，
座垫离地面的距离，
答：座垫离地面的距离约为．
【解析】【分析】（1）根据题意可知∠CAB=90°，利用勾股定理进行计算即可得出BC的值；
（2）过点作，垂足为，根据已知可求出的长，然后根据，得直角三角形利用锐角三角函数的定义求出的长，再加上车轮半径即可．
（1）解：，
，
在中，，，
，
下管的长为；
（2）解：过点作，垂足为，
，，
，
在中，，
，
座垫离地面的距离，
座垫离地面的距离约为．
16．【答案】解：（1）将抛物线 y＝x2﹣x+30转化成顶点式为： y＝（x-40）2+14，
∴对称轴为x=40，
∴BD=40×2=80米，
当x=0时，y=30，
∴AB=30米，
答： 电线杆AB和线段BD的长分别是30米，80米；
（2）根据（1）可知： 抛物线y＝x2﹣x+30的对称轴是x=40，BF=80米，A（0，30），则点C（80，30），
根据题意可知，BM=30米，
∴ 左边抛物线F1 的顶点为（20，18），
设左边抛物线F1的解析式为y1=a（x-20）2+18，
把点A（0，30）代入得：30=202a+18，
∴a=0.03，
∴左边抛物线F1的解析式为y1=0.03（x-20）2+18
把x=30代入F1的解析式得：y1=0.03（30-20）2+18=21，
∴MN=21米，
答：MN的长21米；
（3）由题意可知：MN=CD=30米，
根据抛物线的对称性可知，抛物线F2的顶点在线段CN的垂直平分线上，
∴抛物线F2的顶点的横坐标为+m=+40，
设抛物线F2的顶点的坐标为（+40，n），则抛物线F2的解析式为：y＝(x﹣﹣40)2+n，
将C(80，30)代入得：(80﹣﹣40)2+n＝30，
解得：n＝﹣(40﹣m)2+30，
∴n＝﹣(m﹣80)2+30，
∴n是关于m的二次函数，
又∵由已知m＜80，在对称轴的左侧，
∴n随m的增大而增大，
∴当n＝20时，﹣(m﹣80)2+30＝20，
解得：m1＝40，m2＝120(不符合题意，舍去)，
当n＝25时，﹣(m﹣80)2+30＝25，
解得：m1＝60，m2＝100(不符合题意，舍去)，
∴m的取值范围是：40≤m≤60；
【解析】【分析】(1)将抛物线 y＝x2﹣x+30转化成顶点式为： y＝（x-40）2+14可得对称轴为x＝40，继而得BD，AB的长即可；
(2)由(1)可知， 抛物线y＝x2﹣x+30的对称轴是x=40，BF=80米，A（0，30），则点C（80，30）， 左边抛物线F1 的顶点为(20，18)，设顶点式解析式y1=a（x-20）2+18，把点A（0，30）代入解得a＝0.03，当x＝30时，MN的长度为21米；
(3)根据抛物线的对称性可知抛物线F2的顶点在线段CN的垂直平分线上，可得抛物线F2的顶点的横坐标为+40，设抛物线F2的顶点的坐标为（+40，n），则抛物线F2的解析式为：y＝(x﹣﹣40)2+n，把C(80，30)代入得n＝﹣(m﹣80)2+30，分别求出
n=20与n=25时对应的m值，继而可得m的取值范围是：40≤m≤60.
17．【答案】解：任务一：∵抛物线的顶点坐标为：（100，45），
∴设抛物线的解析式为y=a(x-100)2+45，
∵点P（0，25）在抛物线上，
∴a(x-100)2+45=25，解得：a=-，
所以抛物线的解析式为y=-(x-100)2+45；
任务二：不能实现，理由如下：
击球点为R（300，20），
球网上方点F的坐标为（140，14），
设直线RO解析式为：y=kx，
∴300k=20，
解得：k=，
∴直线RO解析式为y=x，
当x=140时，y=，14=，
所以不能实现；
任务三：设弹起后抛物线的表达式为：y=a1(x-300)2+40，
当a1=a时，y=-(x-300)2+40，
当y=0时， -(x-300)2+40=0，
解得：x=250或x=-50，
∴点M的坐标为（250，0），
∵点M在抛物线y=a1(x-300)2+40上，
∴a1(250-300)2+40=0，
解得：a1=，
∴弹起后抛物线的表达式为：y=(x-300)2+40，
∵a=，
∴弹起时最大高度为40cm，
∴弹起高度范围为30≤y≤40，
当y=30时，(x-300)2+40=30，
解得：x=275或x=325，
∵ 当x=300时，y=40，275<300<325，
∴击球点与发球机水平距离 的取值范围为275【解析】【分析】任务一：根据抛物线的顶点坐标，设出顶点式，将点P的坐标代入，求出a，得出抛物线的解析式；
任务二：先判断不能实现，再说明理由.
设直线RO解析式为：y=kx，将R点坐标代入，求出k，得到直线RO的解析式，将x=140代入，求出函数值与14比较，说明不能实现；
任务三：设弹起后抛物线的表达式为：y=a1(x-300)2+40，
当a1=a时，取y=0，求出点M的坐标，根据点M在抛物线y=a1(x-300)2+40上，求出a1，从而，可得弹起高度范围，取y=30，求出x的值，得出击球点与发球机水平距离 的取值范围.
18．【答案】（1）解：（1）①将代入可得，解得：，
∴该二次函数的表达式为；
②∵将平面内一点向左平移个单位，则与图象上的点重合；若将点A向右平移个单位，则与图象上的点重合，
∴，
∵，
∴抛物线的对称轴为：，
∴，解得：，
∴，
∴．
（2）解：∵设点，是该函数图象上的两点，
∴
∴，，
∴
，
∵，
∴，即．
【解析】【分析】
（1）①利用待定系数法将代入二次函数解析式即可；
②由于B、C两点的纵坐标相同，则B、C两点关于抛物线的对称轴对称，此时可利用抛物线解析式得到对称轴的表达式从而求出的值，再利用二次函数图象上点的坐标特征代入点坐标即可求得n；
（2）由于 与和是定值，则可用含的代数式表示，则可分别用含的代数式表示出与的和，最后再使用配方法即可．
19．【答案】（1）解：当时，则，把点代入得，，
∴，
∴，即；
（2）解：∵，
∴抛物线与轴的交点为，
∴抛物线的对称轴为直线，
∴，
∴对称轴为直线，
∵抛物线开口向上且当时，随的增大而减小，
∴，
∴；
（3）证明：∵函数的图象经过，两点（是实数），
∴，，
∴
，
∵，
∴，，
∴．
【解析】【分析】 本题考查待定系数法求二次函数的解析式，二次函数的性质，二次函数图象上点的坐标特征.（1）当时，则，把点代入解析式可列出方程，解方程可求出n的值，据此可求出函数表达式.
（2）先求出抛物线与的交点坐标，进而可求出抛物线的对称轴为直线，根据抛物线开口向上且当时，随的增大而减小，利用二次函数的性质即可得出，解不等式可求出m的取值范围；
（3）把，两点代入，表示出和为，，然后将配方可得：，利用二次函数的性质可求出最大值和最小值，进而可证明结论．
20．【答案】（1）解：把，，代入中得：
解得，
所以解析式为：；
（2）解：①点的横坐标是，
的纵坐标是
由，求得直线解析式为
的纵坐标是，
所以当时，
②存在，理由如下：
点在直线上，
点的横坐标是
，当时，最大
点坐标为．
【解析】【分析】（1）已知抛物线上三个点的坐标，可利用待定系数法求解；
（2）
①先利用待定系数法求出直线的解析式，由于DF垂直x轴交直线BC于点H，则D、H、F三点的横坐标相同，由于点D在抛物线上，此时可设出点D的坐标，则可表示出点H的坐标，则DH的长度是关于点D横坐标的二次函数，利用二次函数图象上点的坐标特征代入计算即可；
②利用点D的坐标可得出DG的长，则DG+DH的长依然是关于点D横坐标的二次函数，再利用二次函数的增减性即可求解．
21．【答案】（1）证明：∵CD⊥AB，EF∥CD，
∴∠CDB=∠ACB=∠AEF=90°
∴∠B+∠BCD=∠A+∠B
∴∠A=∠BCD
在△AEF和△CDB中，
，
∴△AEF≌△CDB（ASA）.
（2）解：由（1）可知，△AEF≌△CDB，
AF=BC，
∴CF=AC-AF=AC-BC=2.
22．【答案】（1）证明：∵D，E分别是，的中点，
∴，，
∵，
∴，，
∴四边形是平行四边形；
（2）解：①设与交于点H，
∵G是的中点，
∴，
∵四边形是平行四边形，
∴，，，
设，则，
∵，
，
∴，
∴，
∵，
∴，，
∵，
∴，
∵，，
∴，，
∴，
∵，
∴是等腰直角三角形，
∵，
∴，
②由①知，，
∴，
在中，根据勾股定理得：
，
∴平行四边形的周长．
23．【答案】（1）解：∵，
∴，
∴，
∵
∴，
∵DE=4，
∴，
∴CD=.
（2）解：解：连接，如图所示：
∵，P为的中点，，
∴，
∴点P运动的轨迹是以C为圆心，2为半径的圆上的一段弧，
当时，为等边三角形，；
当时，，得到弧的圆心角为，
∴点P运动的路程为圆心角为的弧的长度，即为.
答： 点 P运动的路程是.
（3）解：如图，在上取一点F，使得，连接，，
由（2）可知，，
∵，，
∴，
∵，
∴，
∴，
∴，
∴，
在Rt△ACF中，，
∵，
∴，
∴的最小值为．
24．【答案】（1）证明：连接，如图所示，
为的直径
∴90°，
是的切线.
（2）解：①连接，如图所示，
是的中点
为的直径
∴∠ACB=∠DFO，
，
，
设的半径为，则，，
，，
，
，解得，
经检验，是方程的解，
，
，
，
②过点作交于点，如图所示，
∵是的角平分线，，
，
∴∠CBG=∠BCP，
∴BG=CG，
由（2）①得：，BC=8，
在Rt△BCG中，BC==，即=8，
∴BG=，
∴tan∠BPC=，
∴PG=，
∴CP=CG+PG=.
【解析】【分析】（1）根据，可知，再根据圆周角定理得出∴90°，从而得到，即可证明；
（2）①连接，证明，进而得出，设的半径为，利用相似三角形的性质得，，由勾股定理求得=8，得到，即可得到；
②过点作交于点，推出∴BG=CG，解直角三角形得到，易得tan∠BPC=，解得，由即可求解．
（1）证明：如图，连接，
为的直径
是的切线
（2）解：①如图，连接，
是的中点
为的直径
设的半径为，则，
，
，解得
经检验，是方程的解
②如图，过点作交于点，
，是的角平分线
．
25．【答案】（1）解：是直径，
∴，
∴，
∵，
∴，
∵，
∴．
（2）解：设，则，∵，
∴，
∵，
∴，
∵是等腰三角形，
∴a.当时，，
∴，解得：，
∴；
b：当时，，
∴，
∴，解得：，
∴；
c. 当时，，
∴，解得：，即三点共线，不符合题意；
综上，的度数为和．
②如图：连接并延长交于G，连接，则，
∵，
∴，
∵是的直径，
∴，
设圆的直径为d，
∴，
∴，
∵，
∴
∴，
∴，
∵，
∴，即，
∴，
∴
∵，，
∴，解得：，
∴，
∴，
∵，，
∴，
∴，
∴，即．
【解析】【分析】
（1）由圆周角定理可知等于、是直角，再由等角的余角相等即可得证；
（2）由于，所以EB不可能等于EC，因此当是等腰三角形时只有两种可能，即CE＝CB或BE＝BC，分类讨论并计算即可；
由于锐角三角函数离不开直角三角形，因此可连接OD构造直角三角形，利用圆周角定理把转化到直角三角形ABD中，由AB＝AC，则由垂径定理知半径AO必然垂直平分BC，因此可连接AO并延长交BC于点G，则BG＝CG，且等于等于，此时再设出AD的长，则利用解直角三角形可分别求出AB、BC的长，再利用同角的余角相等可得也等于，解直角三角形可得BH、CH、CF的长，再利用平行线的性质证，从而利用相似比可求出结果．
26．【答案】（1）证明：∵为的直径，，
∴，
∴，
∵，
∴，
∴，
∵为的直径，
∴，
，
，
∴，
∴，即为的中点；
（2）解：①，且，，
∴，
∴设，，
∴，
∵为的直径，，
∴，
∴，
∵，，
∴，
∴，
∴，
，
∴，
∴；
②∵射线与射线相交与点，
∴，
（i）如图，当时，，由（1）得，
，
设，
∴，
由（1）得，
∴，
；
（ii）如图，当时，，
，
∴四边形为平行四边形，
∵，
∴，
∴四边形为菱形，
∵，
∴四边形为正方形，
，
∴；
综上所述，的正切值为或1.
【解析】【分析】（1）根据垂径定理得，根据圆周角定理得，从而得，进而得，根据直径所对的圆周角是直角得，于是得，则有，即可得证结论；
（2）①根据，设，，利用勾股定理、垂径定理得，于是得，然后根据“母子”相似模型证出，从而得，进而求出，代入数据即可求；
②根据题意可知，然后两种情况讨论：（i）当时，先求出，设，得，从而得，进而得；（ii）当时，证出四边形为正方形，从而得，进而根据特殊角的三角函数值可知.
21世纪教育网(www.21cnjy.com)
1 / 1