鲁教版(五四制)九年级上册数学 1.2.2反比例函数的图象与性质(2) 课件(共24张PPT)
文档属性
| 名称 | 鲁教版(五四制)九年级上册数学 1.2.2反比例函数的图象与性质(2) 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-14 15:46:44 | ||
图片预览





文档简介
(共24张PPT)
鲁教版数学(五四制)九年级上册课件
1.2.2反比例函数的图象与性质(2)
《目录》
1
新课导入
2
新知讲解
3
整体感知
《01》
新课导入
Click here to enter your text and change the color or size of the text. Insert the data text icon, change the picture, and have a good time.contents
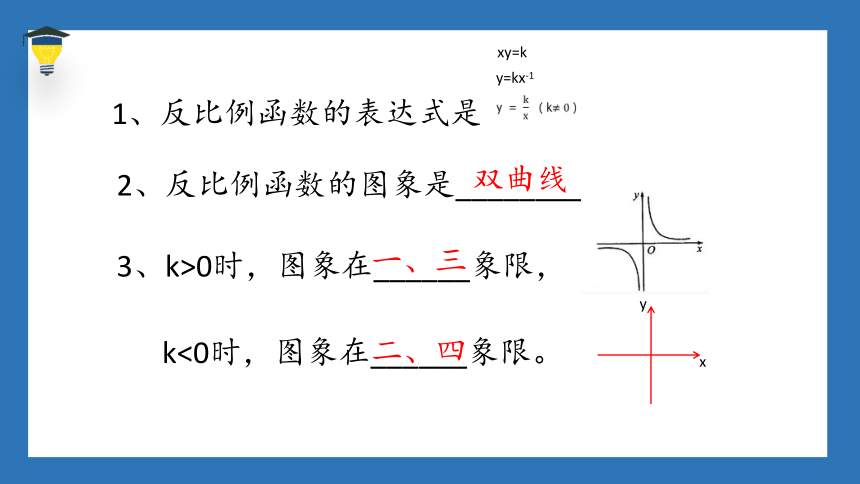
2、反比例函数的图象是_________。
3、k>0时,图象在______象限,
k<0时,图象在______象限。
双曲线
一、三
二、四
1、反比例函数的表达式是______
x
y
y=kx-1
xy=k
1
结合反比例函数的图象,进一步掌握反比例函数的性质,提高从图象中获取信息的能力。
3
能利用反比例函数的增减性,比较函数值的大小。
2
探究并掌握反比例函数的增减性,体会分类讨论的思想。
利用函数图象,理解反比例函数中k的几何意义,渗透数形结合思想。
4
《02》
新知讲解
Click here to enter your text and change the color or size of the text. Insert the data text icon, change the picture, and have a good time.contents
x
y
x
x
y
y
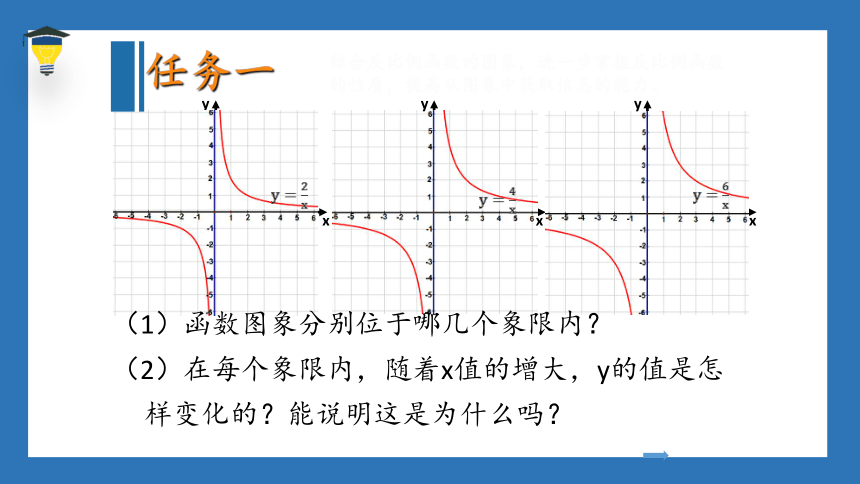
(1)函数图象分别位于哪几个象限内?
任务一
结合反比例函数的图象,进一步掌握反比例函数的性质,提高从图象中获取信息的能力。
(2)在每个象限内,随着x值的增大,y的值是怎
样变化的?能说明这是为什么吗?
X
y
y变小
x
y
O
A
x1
y1
B
x2
y2
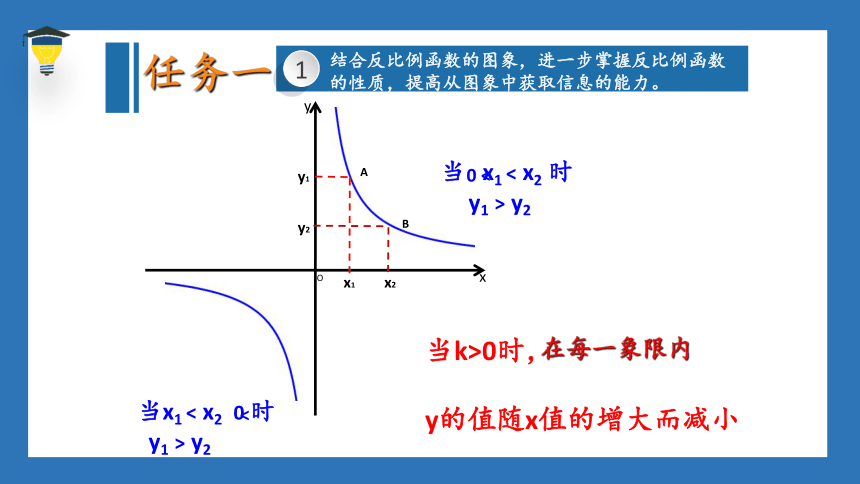
当k>0时,
y的值随x值的增大而减小
任务一
在每一象限内
当 x1 < x2 时
y1 > y2
0 <
当x1 < x2 0 时
y1 > y2
<
1
结合反比例函数的图象,进一步掌握反比例函数的性质,提高从图象中获取信息的能力。
x
y
x
x
y
y
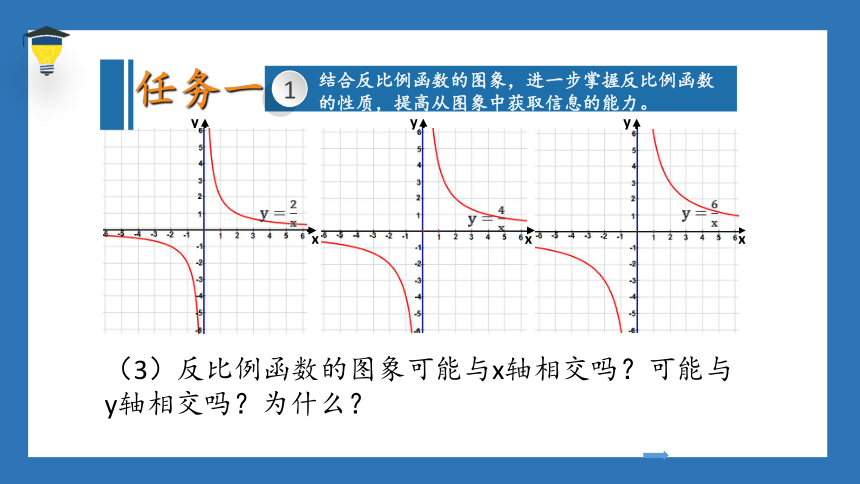
(3)反比例函数的图象可能与x轴相交吗?可能与y轴相交吗?为什么?
任务一
1
结合反比例函数的图象,进一步掌握反比例函数的性质,提高从图象中获取信息的能力。
x
y
x
x
y
y
思考:当k=-2,-4,-6时,反比例函数图象有哪些共同特征?
当k<0时,在每一象限内,y的值随x值的增大而增大。
当 0 < x1 < x2 时
y1 < y2
当 x1 < x2 < 0 时
y1 < y2
反比例函数 的图象:
增减性:
当k>0时,在每一象限内,y的值随x值的增大而减小;
当k<0时,在每一象限内,y的值随x值的增大而增大。
x
y
x
y
当x值的绝对值无限增大时,反比例函数图象的两个分支都无限接近x轴;
当x值的绝对值无限接近于零时,反比例函数图象的两个分支都无限接近y轴。
但永远不会与x轴和y轴相交。
若反比例函数的图象经过点A(-3,6).
解:
(1)
设反比例函数的关系式为
将A(-3,6)的坐标代入 中,得
解得 k=-18.
所以这个反比例函数的表达式为
(2)因为k=-18<0,
所以在每一象限内,y的值随x值的增大而增大。
又 a>b>0
所以 m>n
(1)求这个反比例函数的表达式;
(2)在这个函数的图象上任取点A(a,m)和点B(b,n),
若a>b>0,
那么m和n有怎样的大小关系?
《03》
整体感知
Click here to enter your text and change the color or size of the text. Insert the data text icon, change the picture, and have a good time.contents
若反比例函数的图象经过点A(-3,6).
解:
(1)
设反比例函数的关系式为
将A(-3,6)的坐标代入 中,得
解得 k=-18.
所以这个反比例函数的表达式为
(1)求这个反比例函数的表达式;
(2)在这个函数的图象上任取点A(a,m)和点B(b,n)
若 那么m和n有怎样的大小关系?
a>b>0,
aa>0>b,
(2)因为k=-18<0,
所以在每一象限内,y的值随x值的增大而增大。
又 a所以 my
x
A(a,m)
B(b,n)
n > m
A、y1>y2>y3 B、y2>y1>y3
C、y3>y1>y2 D、y3>y2>y1
C
3
能利用反比例函数的增减性,比较函数值的大小。
评测一
若点A(x1,y1),B(x2,y2),C(x3,y3)在
反比例函数 的图象上,且 x1则( )
若点A(-2,y1),B(-1,y2),C(2,y3)在
反比例函数 的图象上,
则( )
3
能利用反比例函数的增减性,比较函数值的大小。
评测一
已知点(x1,y1),(x2,y2)都在反比例函数
的图象上,且x1>x2,
比较y1与y2的大小.
解:
y1 y2
若两点在同一象限内,则
若两点不在同一象限内,则
y1 y2
<
>
K的几何意义:
x
O
B
A
y
x
O
y
A
B
C
任务二
利用函数图象,理解反比例函数中k的几何意义,渗透数形结合思想。
4
已知点 P(3,2),Q(-2,a)都在反比例函数
的图象上.
过点P分别作两坐标轴的垂线,垂线与两坐标轴围成
的矩形面积为S1;过点Q分别作两坐标轴的垂线,垂
线与两坐标轴围成的矩形面积为S2.
则S1 = ,S2 = , a= .
6
6
-3
任务二
利用函数图象,理解反比例函数中k的几何意义,渗透数形结合思想。
4
我学会了...
使我感触最深的是…
我还感到疑惑的是…
回 扣 目 标
反比例函数
解析式
图象
过点(1,k)
双曲线
性质
增减性
对称性
等面积
颗粒归仓
数形结合
已知点A(-6,y1)、B(-4,y2)在反比例函数
的图象上,试比较y1与y2的大小。
2. 已知点 C(4,y3)、 D(6,y4)在反比例函数
的图象上,试比较y3与y4的大小.
3. 已知点E(-4,y5)、F(6,y6)在反比例函数
的图象上,试比较y5与y6的大小.
y1>y2
y3>y4
y5知识检测
蓄力远航
1-6颗 你掌握了一定的数学基础知识和基本技能,今后若能再注重数学基本思想和方法的应用,成功就会属于你!
7-14颗 你不仅掌握了基础知识和基本技能,还能够注重解题思路和方法的灵活运用,很棒
15-20颗 你的数学素养很好,有着数学家的思维和才智,祝贺你!
星级评价
阳光作业
必做:课本13页,习题 1、2
选做:课本14页,联系拓广
鲁教版数学(五四制)九年级上册课件
1.2.2反比例函数的图象与性质(2)
鲁教版数学(五四制)九年级上册课件
1.2.2反比例函数的图象与性质(2)
《目录》
1
新课导入
2
新知讲解
3
整体感知
《01》
新课导入
Click here to enter your text and change the color or size of the text. Insert the data text icon, change the picture, and have a good time.contents
2、反比例函数的图象是_________。
3、k>0时,图象在______象限,
k<0时,图象在______象限。
双曲线
一、三
二、四
1、反比例函数的表达式是______
x
y
y=kx-1
xy=k
1
结合反比例函数的图象,进一步掌握反比例函数的性质,提高从图象中获取信息的能力。
3
能利用反比例函数的增减性,比较函数值的大小。
2
探究并掌握反比例函数的增减性,体会分类讨论的思想。
利用函数图象,理解反比例函数中k的几何意义,渗透数形结合思想。
4
《02》
新知讲解
Click here to enter your text and change the color or size of the text. Insert the data text icon, change the picture, and have a good time.contents
x
y
x
x
y
y
(1)函数图象分别位于哪几个象限内?
任务一
结合反比例函数的图象,进一步掌握反比例函数的性质,提高从图象中获取信息的能力。
(2)在每个象限内,随着x值的增大,y的值是怎
样变化的?能说明这是为什么吗?
X
y
y变小
x
y
O
A
x1
y1
B
x2
y2
当k>0时,
y的值随x值的增大而减小
任务一
在每一象限内
当 x1 < x2 时
y1 > y2
0 <
当x1 < x2 0 时
y1 > y2
<
1
结合反比例函数的图象,进一步掌握反比例函数的性质,提高从图象中获取信息的能力。
x
y
x
x
y
y
(3)反比例函数的图象可能与x轴相交吗?可能与y轴相交吗?为什么?
任务一
1
结合反比例函数的图象,进一步掌握反比例函数的性质,提高从图象中获取信息的能力。
x
y
x
x
y
y
思考:当k=-2,-4,-6时,反比例函数图象有哪些共同特征?
当k<0时,在每一象限内,y的值随x值的增大而增大。
当 0 < x1 < x2 时
y1 < y2
当 x1 < x2 < 0 时
y1 < y2
反比例函数 的图象:
增减性:
当k>0时,在每一象限内,y的值随x值的增大而减小;
当k<0时,在每一象限内,y的值随x值的增大而增大。
x
y
x
y
当x值的绝对值无限增大时,反比例函数图象的两个分支都无限接近x轴;
当x值的绝对值无限接近于零时,反比例函数图象的两个分支都无限接近y轴。
但永远不会与x轴和y轴相交。
若反比例函数的图象经过点A(-3,6).
解:
(1)
设反比例函数的关系式为
将A(-3,6)的坐标代入 中,得
解得 k=-18.
所以这个反比例函数的表达式为
(2)因为k=-18<0,
所以在每一象限内,y的值随x值的增大而增大。
又 a>b>0
所以 m>n
(1)求这个反比例函数的表达式;
(2)在这个函数的图象上任取点A(a,m)和点B(b,n),
若a>b>0,
那么m和n有怎样的大小关系?
《03》
整体感知
Click here to enter your text and change the color or size of the text. Insert the data text icon, change the picture, and have a good time.contents
若反比例函数的图象经过点A(-3,6).
解:
(1)
设反比例函数的关系式为
将A(-3,6)的坐标代入 中,得
解得 k=-18.
所以这个反比例函数的表达式为
(1)求这个反比例函数的表达式;
(2)在这个函数的图象上任取点A(a,m)和点B(b,n)
若 那么m和n有怎样的大小关系?
a>b>0,
a
(2)因为k=-18<0,
所以在每一象限内,y的值随x值的增大而增大。
又 a
x
A(a,m)
B(b,n)
n > m
A、y1>y2>y3 B、y2>y1>y3
C、y3>y1>y2 D、y3>y2>y1
C
3
能利用反比例函数的增减性,比较函数值的大小。
评测一
若点A(x1,y1),B(x2,y2),C(x3,y3)在
反比例函数 的图象上,且 x1
若点A(-2,y1),B(-1,y2),C(2,y3)在
反比例函数 的图象上,
则( )
3
能利用反比例函数的增减性,比较函数值的大小。
评测一
已知点(x1,y1),(x2,y2)都在反比例函数
的图象上,且x1>x2,
比较y1与y2的大小.
解:
y1 y2
若两点在同一象限内,则
若两点不在同一象限内,则
y1 y2
<
>
K的几何意义:
x
O
B
A
y
x
O
y
A
B
C
任务二
利用函数图象,理解反比例函数中k的几何意义,渗透数形结合思想。
4
已知点 P(3,2),Q(-2,a)都在反比例函数
的图象上.
过点P分别作两坐标轴的垂线,垂线与两坐标轴围成
的矩形面积为S1;过点Q分别作两坐标轴的垂线,垂
线与两坐标轴围成的矩形面积为S2.
则S1 = ,S2 = , a= .
6
6
-3
任务二
利用函数图象,理解反比例函数中k的几何意义,渗透数形结合思想。
4
我学会了...
使我感触最深的是…
我还感到疑惑的是…
回 扣 目 标
反比例函数
解析式
图象
过点(1,k)
双曲线
性质
增减性
对称性
等面积
颗粒归仓
数形结合
已知点A(-6,y1)、B(-4,y2)在反比例函数
的图象上,试比较y1与y2的大小。
2. 已知点 C(4,y3)、 D(6,y4)在反比例函数
的图象上,试比较y3与y4的大小.
3. 已知点E(-4,y5)、F(6,y6)在反比例函数
的图象上,试比较y5与y6的大小.
y1>y2
y3>y4
y5
蓄力远航
1-6颗 你掌握了一定的数学基础知识和基本技能,今后若能再注重数学基本思想和方法的应用,成功就会属于你!
7-14颗 你不仅掌握了基础知识和基本技能,还能够注重解题思路和方法的灵活运用,很棒
15-20颗 你的数学素养很好,有着数学家的思维和才智,祝贺你!
星级评价
阳光作业
必做:课本13页,习题 1、2
选做:课本14页,联系拓广
鲁教版数学(五四制)九年级上册课件
1.2.2反比例函数的图象与性质(2)
