2025年中考数学二轮复习-专题1平面直角坐标系中三角形的面积【课件】(共27张PPT)
文档属性
| 名称 | 2025年中考数学二轮复习-专题1平面直角坐标系中三角形的面积【课件】(共27张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 798.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-14 00:00:00 | ||
图片预览




文档简介
(共27张PPT)
专题一 平面直角坐标系中三角形的面积
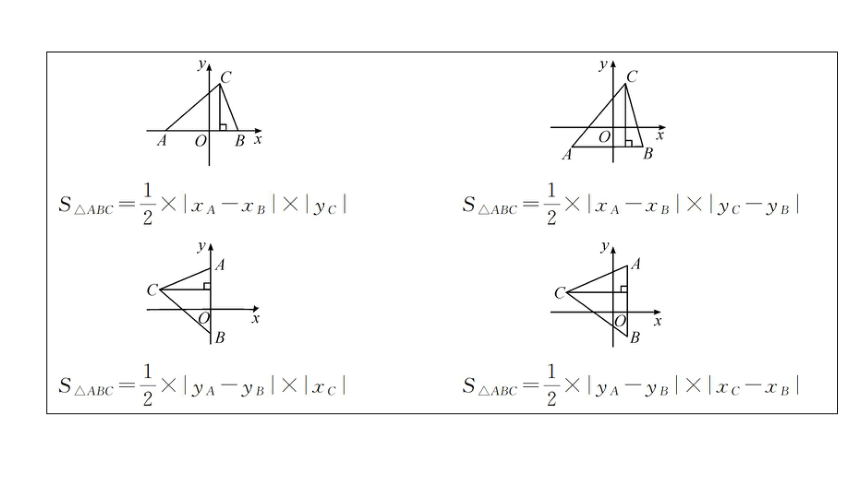
类型一 三角形有一边在坐标轴上或与坐标轴平行
当三角形有一边在坐标轴上或与坐标轴平行时,通常以与坐标轴
平行的边为底边,利用“S△= ×底×高”进行计算.若AB∥x轴,则
AB= ;若AB∥y轴,则AB= .
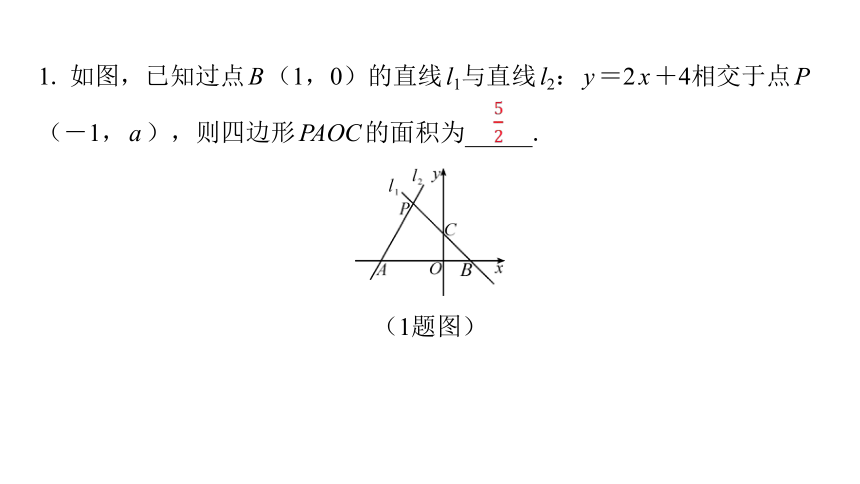
1. 如图,已知过点B(1,0)的直线l1与直线l2:y=2x+4相交于点P
(-1,a),则四边形PAOC的面积为 .
(1题图)
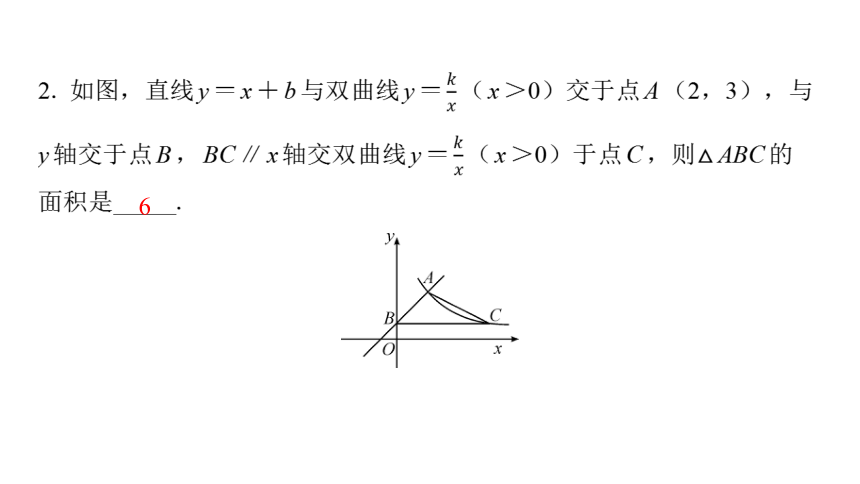
2. 如图,直线y=x+b与双曲线y= (x>0)交于点A(2,3),与
y轴交于点B,BC∥x轴交双曲线y= (x>0)于点C,则△ABC的
面积是 .
6
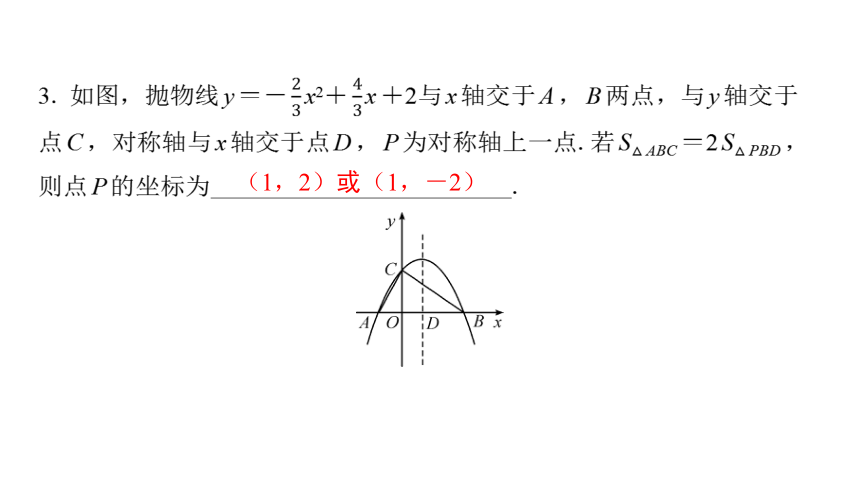
3. 如图,抛物线y=- x2+ x+2与x轴交于A,B两点,与y轴交于
点C,对称轴与x轴交于点D,P为对称轴上一点.若S△ABC=2S△PBD,
则点P的坐标为 .
(1,2)或(1,-2)
4. [2024·苏州]如图,△ABC中,AC=BC,∠ACB=90°,A(-2,
0),C(6,0),反比例函数y= (k≠0,x>0)的图象与AB交于
点D(m,4),与BC交于点E.
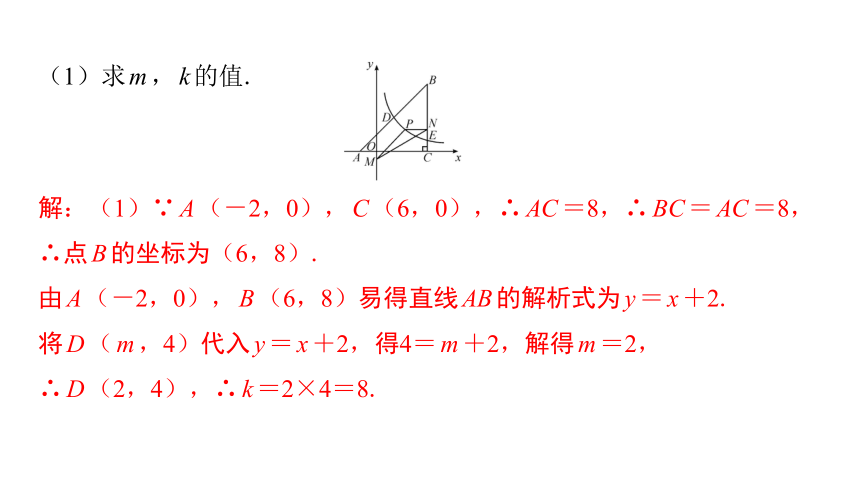
(1)求m,k的值.
解:(1)∵A(-2,0),C(6,0),∴AC=8,∴BC=AC=8,
∴点B的坐标为(6,8).
由A(-2,0),B(6,8)易得直线AB的解析式为y=x+2.
将D(m,4)代入y=x+2,得4=m+2,解得m=2,
∴D(2,4),∴k=2×4=8.
(2)P为反比例函数y= (k≠0,x>0)图象上一动点(点P在D,
E之间运动,不与D,E重合).过点P作PM∥AB,交y轴于点M,过
点P作PN∥x轴,交BC于点N,连接MN,求△PMN面积的最大值,
并求出此时点P的坐标.
解:(2)如图,延长NP交y轴于点G,交AB于点H.
∵BC=AC,∠ACB=90°,∴∠BAC=45°.
∵PN∥x轴,PM∥AB,∴∠GPM=∠BHN=∠BAC=45°,∴PG=MG.
易得E(6, ).设P(t, ),且2<t<6,则MG=PG=t,
PN=6-t,
∴S△PMN= PN·MG= ×(6-t)×t=- (t-3)2+ ,
∴当t=3时,△PMN面积有最大值,最大值为 ,此时
点P的坐标为(3, ).
类型二 三角形的三边与坐标轴都不平行
当三角形的三边与坐标轴都不平行时,常利用“补形”或“分
形”进行三角形面积的转化.
(1)补形:S△ABC=SRt△ABD-S△ACD-S△BCD;S△ABC=S矩形EFBD
-S△ABF-S△BCD-S△ACE.
(2)分形:竖分△ABC,S△ABC= AD· ;横分
△ABC,S△ABC= CD· .
1. 如图,在平面直角坐标系中,已知A(3,2),B(4,1),则
△AOB的面积是 .
2. 如图,直线AB与双曲线交于A(1,6),B(m,-2)两点,直线
BO与双曲线在第一象限交于点C,连接AC,则△ABC的面积
为 .
16
3. 如图,二次函数图象与x轴交于A(-1,0),B(5,0),与y轴
交于点C,顶点为D,tan∠ACO= ,则四边形ACDB的面积
是 .
30
4. 如图,抛物线y=-x2-2x+3与x轴交于A,B两点,与y轴交于点
C,过点B的直线m∥AC,E是直线AC上方抛物线上一动点,H为直
线m上一动点,连接AE,EC,CH,CB,AH,当四边形AHCE面积
最大时,求点E的坐标.
解:由y=-x2-2x+3易得A(-3,0),B(1,0),C(0,3).
∵直线m∥AC,∴S△AHC=S△ABC= AB·OC= ×4×3=6.
∵S四边形AHCE=S△AEC+S△AHC=S△AEC+6,
∴当△AEC的面积最大时,四边形AHCE的面积最大.
由A(-3,0),C(0,3)易得直线AC的解析式为y=x+3.
如图,过点E作EF∥y轴,交AC于点F. 设E(t,-t2-2t+3),则
F(t,t+3),
∴EF=-t2-2t+3-(t+3)=-t2-3t,∴S△AEC= EF· = ×
(-t2-3t)×3,
整理可得S△AEC=- + ,∴当t=- 时,△AEC的面积
最大,
当t=- 时,-t2-2t+3=- -2×(- )+3= ,
∴当四边形AHCE面积最大时,点E的坐标为(- , ).
5. 如图,抛物线y=ax2+bx+c 与x轴交于点A(-1,0),B(3,
0),与y轴交于点C(0,-3),Q为线段BC上的动点.
(1)求抛物线的解析式.
解:(1)抛物线的解析式为y=x2-2x-3.
(2)如图①,求OQ+AQ的最小值.
解:(2)易得直线BC的解析式为y=x-3.
如图①,作点O关于直线BC的对称点D,连接AD交BC于点Q,则
OQ+AQ=DQ+AQ,由“两点之间,线段最短”可得OQ+AQ的最
小值为线段AD的长.
∵△OCB为等腰直角三角形,∴D(3,-3).∵DB⊥x轴,
∴AD= =5,即OQ+AQ的最小值为5.
(3)如图②,过点Q作PQ∥AC,交抛物线的第四象限部分于点P,
连接PA,PB,记△PAQ与△PBQ的面积分别为S1,S2.设S=S1+S2,
求使得S最大的点P的坐标,并求出S的最大值.
解:(3)如图②,连接PC,过点P作PN∥y轴,交BC于点N.
∵PQ∥AC,∴S1=S△PAQ=S△PCQ,∴S=S△PBC.
设P(m,m2-2m-3),则N(m,m-3),∴PN=m-3-(m2
-2m-3)=-m2+3m,
∴S=S△PBC= PN·OB= ×(-m2+3m)×3,即S=- m2+ m
=- + .
∵0<m<3,∴当m= 时,S最大= ,∴当点P的坐标为( ,-
)时,S有最大值为 .
谢谢观看
专题一 平面直角坐标系中三角形的面积
类型一 三角形有一边在坐标轴上或与坐标轴平行
当三角形有一边在坐标轴上或与坐标轴平行时,通常以与坐标轴
平行的边为底边,利用“S△= ×底×高”进行计算.若AB∥x轴,则
AB= ;若AB∥y轴,则AB= .
1. 如图,已知过点B(1,0)的直线l1与直线l2:y=2x+4相交于点P
(-1,a),则四边形PAOC的面积为 .
(1题图)
2. 如图,直线y=x+b与双曲线y= (x>0)交于点A(2,3),与
y轴交于点B,BC∥x轴交双曲线y= (x>0)于点C,则△ABC的
面积是 .
6
3. 如图,抛物线y=- x2+ x+2与x轴交于A,B两点,与y轴交于
点C,对称轴与x轴交于点D,P为对称轴上一点.若S△ABC=2S△PBD,
则点P的坐标为 .
(1,2)或(1,-2)
4. [2024·苏州]如图,△ABC中,AC=BC,∠ACB=90°,A(-2,
0),C(6,0),反比例函数y= (k≠0,x>0)的图象与AB交于
点D(m,4),与BC交于点E.
(1)求m,k的值.
解:(1)∵A(-2,0),C(6,0),∴AC=8,∴BC=AC=8,
∴点B的坐标为(6,8).
由A(-2,0),B(6,8)易得直线AB的解析式为y=x+2.
将D(m,4)代入y=x+2,得4=m+2,解得m=2,
∴D(2,4),∴k=2×4=8.
(2)P为反比例函数y= (k≠0,x>0)图象上一动点(点P在D,
E之间运动,不与D,E重合).过点P作PM∥AB,交y轴于点M,过
点P作PN∥x轴,交BC于点N,连接MN,求△PMN面积的最大值,
并求出此时点P的坐标.
解:(2)如图,延长NP交y轴于点G,交AB于点H.
∵BC=AC,∠ACB=90°,∴∠BAC=45°.
∵PN∥x轴,PM∥AB,∴∠GPM=∠BHN=∠BAC=45°,∴PG=MG.
易得E(6, ).设P(t, ),且2<t<6,则MG=PG=t,
PN=6-t,
∴S△PMN= PN·MG= ×(6-t)×t=- (t-3)2+ ,
∴当t=3时,△PMN面积有最大值,最大值为 ,此时
点P的坐标为(3, ).
类型二 三角形的三边与坐标轴都不平行
当三角形的三边与坐标轴都不平行时,常利用“补形”或“分
形”进行三角形面积的转化.
(1)补形:S△ABC=SRt△ABD-S△ACD-S△BCD;S△ABC=S矩形EFBD
-S△ABF-S△BCD-S△ACE.
(2)分形:竖分△ABC,S△ABC= AD· ;横分
△ABC,S△ABC= CD· .
1. 如图,在平面直角坐标系中,已知A(3,2),B(4,1),则
△AOB的面积是 .
2. 如图,直线AB与双曲线交于A(1,6),B(m,-2)两点,直线
BO与双曲线在第一象限交于点C,连接AC,则△ABC的面积
为 .
16
3. 如图,二次函数图象与x轴交于A(-1,0),B(5,0),与y轴
交于点C,顶点为D,tan∠ACO= ,则四边形ACDB的面积
是 .
30
4. 如图,抛物线y=-x2-2x+3与x轴交于A,B两点,与y轴交于点
C,过点B的直线m∥AC,E是直线AC上方抛物线上一动点,H为直
线m上一动点,连接AE,EC,CH,CB,AH,当四边形AHCE面积
最大时,求点E的坐标.
解:由y=-x2-2x+3易得A(-3,0),B(1,0),C(0,3).
∵直线m∥AC,∴S△AHC=S△ABC= AB·OC= ×4×3=6.
∵S四边形AHCE=S△AEC+S△AHC=S△AEC+6,
∴当△AEC的面积最大时,四边形AHCE的面积最大.
由A(-3,0),C(0,3)易得直线AC的解析式为y=x+3.
如图,过点E作EF∥y轴,交AC于点F. 设E(t,-t2-2t+3),则
F(t,t+3),
∴EF=-t2-2t+3-(t+3)=-t2-3t,∴S△AEC= EF· = ×
(-t2-3t)×3,
整理可得S△AEC=- + ,∴当t=- 时,△AEC的面积
最大,
当t=- 时,-t2-2t+3=- -2×(- )+3= ,
∴当四边形AHCE面积最大时,点E的坐标为(- , ).
5. 如图,抛物线y=ax2+bx+c 与x轴交于点A(-1,0),B(3,
0),与y轴交于点C(0,-3),Q为线段BC上的动点.
(1)求抛物线的解析式.
解:(1)抛物线的解析式为y=x2-2x-3.
(2)如图①,求OQ+AQ的最小值.
解:(2)易得直线BC的解析式为y=x-3.
如图①,作点O关于直线BC的对称点D,连接AD交BC于点Q,则
OQ+AQ=DQ+AQ,由“两点之间,线段最短”可得OQ+AQ的最
小值为线段AD的长.
∵△OCB为等腰直角三角形,∴D(3,-3).∵DB⊥x轴,
∴AD= =5,即OQ+AQ的最小值为5.
(3)如图②,过点Q作PQ∥AC,交抛物线的第四象限部分于点P,
连接PA,PB,记△PAQ与△PBQ的面积分别为S1,S2.设S=S1+S2,
求使得S最大的点P的坐标,并求出S的最大值.
解:(3)如图②,连接PC,过点P作PN∥y轴,交BC于点N.
∵PQ∥AC,∴S1=S△PAQ=S△PCQ,∴S=S△PBC.
设P(m,m2-2m-3),则N(m,m-3),∴PN=m-3-(m2
-2m-3)=-m2+3m,
∴S=S△PBC= PN·OB= ×(-m2+3m)×3,即S=- m2+ m
=- + .
∵0<m<3,∴当m= 时,S最大= ,∴当点P的坐标为( ,-
)时,S有最大值为 .
谢谢观看
同课章节目录
