2025年中考数学二轮复习-专题2与角平分线相关的辅助线添加【课件】(共20张PPT)
文档属性
| 名称 | 2025年中考数学二轮复习-专题2与角平分线相关的辅助线添加【课件】(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 372.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-14 16:33:39 | ||
图片预览






文档简介
(共20张PPT)
专题二 与角平分线相关的辅助线添加
类型一 过角平分线上一点作角两边的垂线构造全等直角三角形
OP平分∠MON,过点P作PA⊥OM于点A,PB⊥ON于点B.
PA=PB,△POA≌△POB.
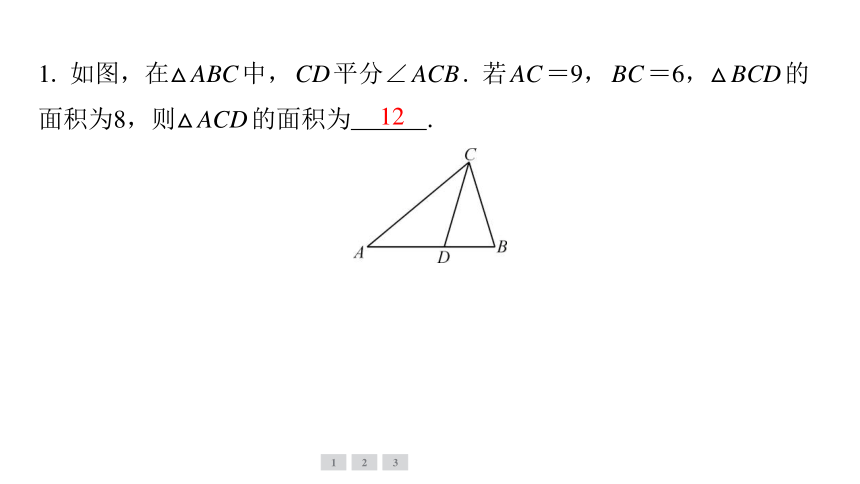
1. 如图,在△ABC中,CD平分∠ACB. 若AC=9,BC=6,△BCD的
面积为8,则△ACD的面积为 .
12
1
2
3
2. 如图,在△ABC中,∠C=90°,AD平分∠CAB,CD= ,BD=
,则AC的长是 .
3
1
2
3
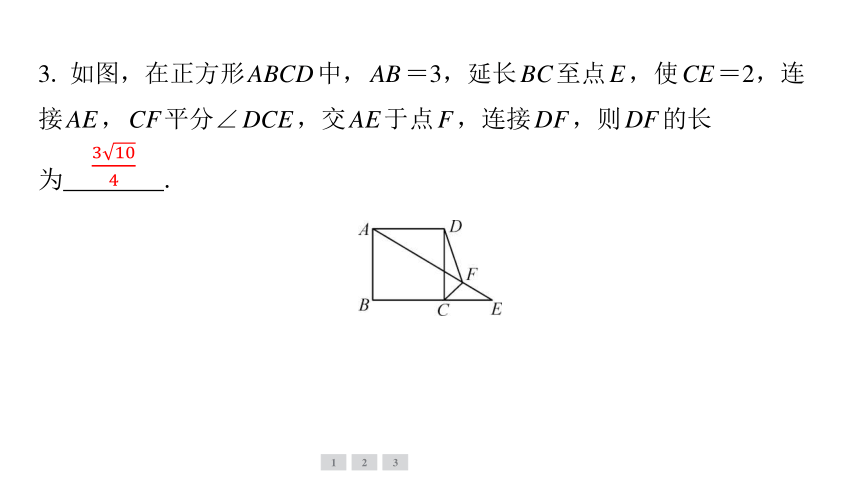
3. 如图,在正方形ABCD中,AB=3,延长BC至点E,使CE=2,连
接AE,CF平分∠DCE,交AE于点F,连接DF,则DF的长
为 .
1
2
3
类型二 过角平分线上一点作角一边的平行线构造等腰三角形
(1)OP平分∠MON,过点P作PA∥ON,交OM于点A PA=
OA.
(2)平行线+角平分线 等腰三角形.
1
2
3
1. 如图,在 ABCD中,CD=4,∠D=30°,BE平分∠ABC,交
AD于点E,则△ABE的面积是 .
4
1
2
3
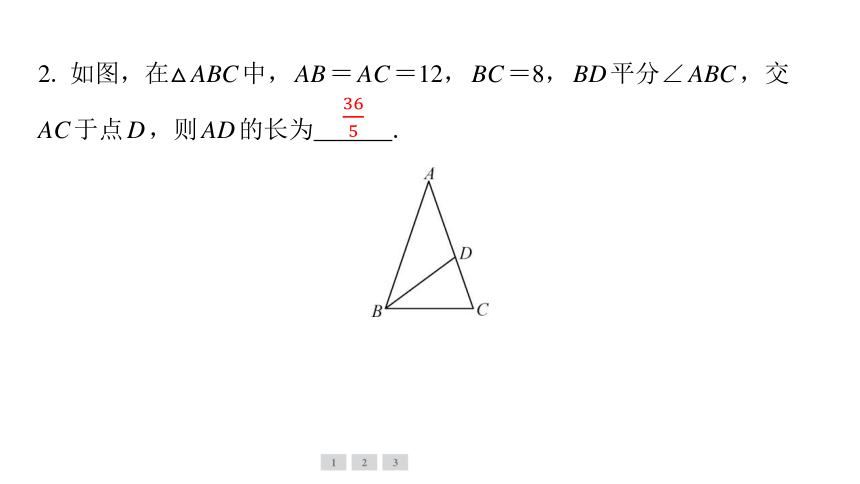
2. 如图,在△ABC中,AB=AC=12,BC=8,BD平分∠ABC,交
AC于点D,则AD的长为 .
1
2
3
3. 如图,在平面直角坐标中,直线y=- x+3分别与x轴、y轴交于
点A,B,C为BC上一点,且AC平分∠OAB,则直线AC的解析式
为 .
y=- x+
1
2
3
类型三 过角平分线上一点作角平分线的垂线构造等腰三角形
(1)OP平分∠MON,PB⊥OP,延长BP交OM于点A OA=
OB.
(2)构造出等腰三角形后,与等腰三角形的“三线合一”性质相
联系.
1
2
3
1. 如图,△ABC的面积为4,AP与∠ABC的平分线垂直,垂足为P,
则△PBC的面积为 .
2
1
2
3
4
2. 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AN平分
∠CAB,CN⊥AN于点N,BM平分∠CBA,CM⊥BM于点M,连接
MN,则MN的长为 .
2
1
2
3
4
3. 如图,在△ABC中,∠C=90°,AB=10,AC=8,AD平分
∠BAC,交BC边于点D,BE⊥AD,交AD的延长线于点E,则BE的
长为 .
1
2
3
4
4. 如图,△ABC内接于☉O,点O在AB上,AD平分∠BAC,交☉O于
点D,连接BD. 若AB=10,BD=2 ,则BC的长为 .
8
1
2
3
4
类型四 通过截长补短构造全等三角形
如图①,AD平分∠BAC→在AC上截取AE=
AB→△ABD≌△AED,BD=ED.
如图②,AD平分∠BAC→延长AB至点E,使得AE=
AC→△AED≌△ACD,ED=CD.
1
2
3
4
1. 如图,在△ABC中,AD平分∠BAC,∠B=2∠C. 求证:
AC=AB+BD.
1
2
证明:如图,在AC上截取AE=AB,连接DE.
∵AD平分∠BAC,∴∠BAD=∠EAD.
又∵AB=AE,AD=AD,∴△ABD≌△AED(SAS),
∴BD=ED,∠AED=∠B.
又∵∠B=∠AED=∠EDC+∠C,∠B=2∠C,∴∠EDC=∠C,
∴EC=ED=BD,∴AC=AE+EC=AB+BD.
1
2
2. 如图,在等边三角形ABC中,E为边AC上一定点,D是BC延长线
上一动点,连接ED,并在其右侧作等边三角形DEF,连接CF. 请探究
CE,CF与CD之间的数量关系,并说明理由.
1
2
解:如图,延长EC至点G,使得CG=CD,连接DG.
∵∠DCG=∠ACB=60°,∴△CDG是等边三角形,
∴DG=DC,∠GDC=60°.
又∵△DEF是等边三角形,∴DE=DF,∠EDF=60°,
∴∠GDC=∠EDF=60°,∴∠GDE=∠CDF,
∴△EDG≌△FDC(SAS),∴CF=EG=CE+CG=CE+CD.
1
2
谢谢观看
专题二 与角平分线相关的辅助线添加
类型一 过角平分线上一点作角两边的垂线构造全等直角三角形
OP平分∠MON,过点P作PA⊥OM于点A,PB⊥ON于点B.
PA=PB,△POA≌△POB.
1. 如图,在△ABC中,CD平分∠ACB. 若AC=9,BC=6,△BCD的
面积为8,则△ACD的面积为 .
12
1
2
3
2. 如图,在△ABC中,∠C=90°,AD平分∠CAB,CD= ,BD=
,则AC的长是 .
3
1
2
3
3. 如图,在正方形ABCD中,AB=3,延长BC至点E,使CE=2,连
接AE,CF平分∠DCE,交AE于点F,连接DF,则DF的长
为 .
1
2
3
类型二 过角平分线上一点作角一边的平行线构造等腰三角形
(1)OP平分∠MON,过点P作PA∥ON,交OM于点A PA=
OA.
(2)平行线+角平分线 等腰三角形.
1
2
3
1. 如图,在 ABCD中,CD=4,∠D=30°,BE平分∠ABC,交
AD于点E,则△ABE的面积是 .
4
1
2
3
2. 如图,在△ABC中,AB=AC=12,BC=8,BD平分∠ABC,交
AC于点D,则AD的长为 .
1
2
3
3. 如图,在平面直角坐标中,直线y=- x+3分别与x轴、y轴交于
点A,B,C为BC上一点,且AC平分∠OAB,则直线AC的解析式
为 .
y=- x+
1
2
3
类型三 过角平分线上一点作角平分线的垂线构造等腰三角形
(1)OP平分∠MON,PB⊥OP,延长BP交OM于点A OA=
OB.
(2)构造出等腰三角形后,与等腰三角形的“三线合一”性质相
联系.
1
2
3
1. 如图,△ABC的面积为4,AP与∠ABC的平分线垂直,垂足为P,
则△PBC的面积为 .
2
1
2
3
4
2. 如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AN平分
∠CAB,CN⊥AN于点N,BM平分∠CBA,CM⊥BM于点M,连接
MN,则MN的长为 .
2
1
2
3
4
3. 如图,在△ABC中,∠C=90°,AB=10,AC=8,AD平分
∠BAC,交BC边于点D,BE⊥AD,交AD的延长线于点E,则BE的
长为 .
1
2
3
4
4. 如图,△ABC内接于☉O,点O在AB上,AD平分∠BAC,交☉O于
点D,连接BD. 若AB=10,BD=2 ,则BC的长为 .
8
1
2
3
4
类型四 通过截长补短构造全等三角形
如图①,AD平分∠BAC→在AC上截取AE=
AB→△ABD≌△AED,BD=ED.
如图②,AD平分∠BAC→延长AB至点E,使得AE=
AC→△AED≌△ACD,ED=CD.
1
2
3
4
1. 如图,在△ABC中,AD平分∠BAC,∠B=2∠C. 求证:
AC=AB+BD.
1
2
证明:如图,在AC上截取AE=AB,连接DE.
∵AD平分∠BAC,∴∠BAD=∠EAD.
又∵AB=AE,AD=AD,∴△ABD≌△AED(SAS),
∴BD=ED,∠AED=∠B.
又∵∠B=∠AED=∠EDC+∠C,∠B=2∠C,∴∠EDC=∠C,
∴EC=ED=BD,∴AC=AE+EC=AB+BD.
1
2
2. 如图,在等边三角形ABC中,E为边AC上一定点,D是BC延长线
上一动点,连接ED,并在其右侧作等边三角形DEF,连接CF. 请探究
CE,CF与CD之间的数量关系,并说明理由.
1
2
解:如图,延长EC至点G,使得CG=CD,连接DG.
∵∠DCG=∠ACB=60°,∴△CDG是等边三角形,
∴DG=DC,∠GDC=60°.
又∵△DEF是等边三角形,∴DE=DF,∠EDF=60°,
∴∠GDC=∠EDF=60°,∴∠GDE=∠CDF,
∴△EDG≌△FDC(SAS),∴CF=EG=CE+CG=CE+CD.
1
2
谢谢观看
同课章节目录
