【核心考点集训】第三单元《圆柱和圆锥》复习检测卷(含答案)--人教版六年级下册数学
文档属性
| 名称 | 【核心考点集训】第三单元《圆柱和圆锥》复习检测卷(含答案)--人教版六年级下册数学 |
|
|
| 格式 | docx | ||
| 文件大小 | 185.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-14 00:00:00 | ||
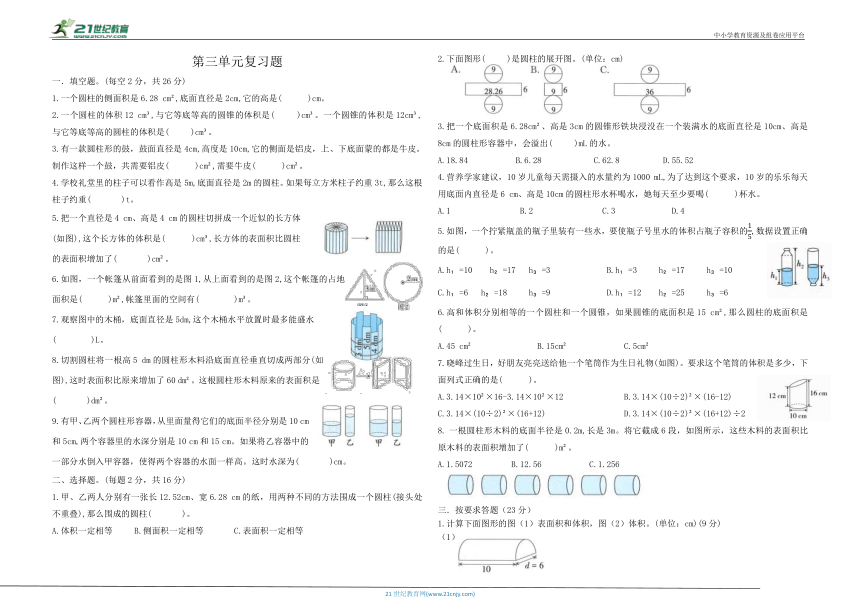
图片预览

文档简介
中小学教育资源及组卷应用平台
第三单元复习题
一.填空题。(每空2分,共26分)
1.一个圆柱的侧面积是6.28 cm ,底面直径是2cm,它的高是( )cm。
2.一个圆柱的体积12 cm ,与它等底等高的圆锥的体积是( )cm 。一个圆锥的体积是12cm ,与它等底等高的圆柱的体积是( )cm 。
3.有一款圆柱形的鼓,鼓面直径是4cm,高度是10cm,它的侧面是铝皮,上、下底面蒙的都是牛皮。制作这样一个鼓,共需要铝皮( )cm ,需要牛皮( )cm 。
4.学校礼堂里的柱子可以看作高是5m,底面直径是2m的圆柱。如果每立方米柱子约重3t,那么这根柱子约重( )t。
5.把一个直径是4 cm、高是4 cm的圆柱切拼成一个近似的长方体(如图),这个长方体的体积是( )cm ,长方体的表面积比圆柱的表面积增加了( )cm 。
6.如图,一个帐篷从前面看到的是图1,从上面看到的是图2,这个帐篷的占地面积是( )m ,帐篷里面的空间有( )m 。
7.观察图中的木桶,底面直径是5dm,这个木桶水平放置时最多能盛水
( )L。
8.切割圆柱将一根高5 dm的圆柱形木料沿底面直径垂直切成两部分(如图),这时表面积比原来增加了60 dm 。这根圆柱形木料原来的表面积是( )dm 。
9.有甲、乙两个圆柱形容器,从里面量得它们的底面半径分别是10 cm和5cm,两个容器里的水深分别是10 cm和15 cm。如果将乙容器中的一部分水倒入甲容器,使得两个容器的水面一样高。这时水深为( )cm。
二、选择题。(每题2分,共16分)
1.甲、乙两人分别有一张长12.52cm、宽6.28 cm的纸,用两种不同的方法围成一个圆柱(接头处不重叠),那么围成的圆柱( )。
A.体积一定相等 B.侧面积一定相等 C.表面积一定相等
2.下面图形( )是圆柱的展开图。(单位:cm)
3.把一个底面积是6.28cm 、高是3cm的圆锥形铁块浸没在一个装满水的底面直径是10cm、高是8cm的圆柱形容器中,会溢出( )mL的水。
A.18.84 B.6.28 C.62.8 D.55.52
4.营养学家建议,10岁儿童每天需摄入的水量约为1000 mL,为了达到这个要求,10岁的乐乐每天用底面内直径是6 cm、高是10cm的圆柱形水杯喝水,她每天至少要喝( )杯水。
A.1 B.2 C.3 D.4
5.如图,一个拧紧瓶盖的瓶子里装有一些水,要使瓶子号里水的体积占瓶子容积的,数据设置正确的是( )。
A.h =10 h =17 h =3 B.h =3 h =17 h =10
C.h =6 h =18 h =9 D.h =12 h =25 h =6
6.高和体积分别相等的一个圆柱和一个圆锥,如果圆锥的底面积是15 cm ,那么圆柱的底面积是( )。
A.45 cm B.15cm C.5cm
7.晓峰过生日,好朋友亮亮送给他一个笔筒作为生日礼物(如图)。要求这个笔筒的体积是多少,下面列式正确的是( )。
A.3.14×10 ×16-3.14×10 ×12 B.3.14×(10÷2) ×(16-12)
C.3.14×(10÷2) ×(16+12) D.3.14×(10÷2) ×(16+12)÷2
一根圆柱形木料的底面半径是0.2m,长是3m。将它截成6段,如图所示,这些木料的表面积比原木料的表面积增加了( )m 。
A.1.5072 B.12.56 C.1.256
三.按要求答题(23分)
1.计算下面图形的图(1)表面积和体积,图(2)体积。(单位:cm)(9分)
(1)
(2)
2.计算图形旋转一周得到的立体图形的体积。(单位:dm)(4分)
3.为了测量一个空瓶子的容积,一个学习小组进行了如下实验。(10分)
①测量出整个瓶子的高度是22 cm;
②测量出整个瓶子圆柱部分的内直径是6 cm;
③给瓶子里注入一些水,把瓶子正放时,测量出水的高度是5cm;
④把瓶子倒放时,无水部分是圆柱形,测量出该圆柱的高是12 cm。
(1)要求这个瓶子的容积,上面记录中哪些信息是必须有的 。(填序号)(3分)
(2)请根据选出的信息,求出这个瓶子的容积。(7分)
四.解决问题(35分)
1.为减少小硕妹妹在学校削铅笔的次数,妈妈把她的铅笔两端都削了削(如图)。已知铅笔的直径是0.8 cm,这支削好的铅笔的体积是多少立方厘米 (6分)
2.妈妈用废旧床单给小硕做了一个圆柱形沙袋,不仅缓解学习压力,还增强体质。沙袋底面周长是6.28 dm,高是3 dm(外层厚度忽略不计)。
(1)做这个沙袋用了多少平方分米废旧床单 (损耗忽略不计)(5分)
(2)等积变形一次沙袋底破了,沙子全部流到地板上形成了一个高2 dm的圆锥形沙堆,这个圆锥形沙堆的占地面积是多少平方分米 (5分)
3.如图,粮仓的总高度为3.5m,它的圆柱部分底面周长为12.56m,圆锥部分高为1.5m。(9分)
(1)不考虑粮仓内壁的厚度,这个粮仓的体积是多少 (4分)
(2)每立方米稻谷大约重0.65t。如果稻谷的出米率是70%,一个粮仓的稻谷大约能出多少吨大米 (粮仓装满稻谷,结果保留两位小数)(5分)
4.如果用如图的玻璃杯喝果汁,一壶果汁正好能倒满8杯。现在用如图的塑料杯喝果汁,同样一壶果汁正好能倒满5杯,塑料杯的高是多少 (5分)
5.“铁质零件总是生锈,应该怎么办呢 ”“将零件浸没在防锈油中就可以了。”将一个长10 cm、宽10cm、高12 cm的长方体铁质零件放入一个底面直径是20cm、高20cm的圆柱形容器中浸防锈油,那么容器内至少需要注人多少升防锈油才能完全将零件浸没
答案:
一.填空。
1. 1
2.4;36
3.125.6;25.12
4.47.1
5.5024;16
6.12.56;12.56
7.58.875
8.150.72
9.11
二.选择
B;A;B;D;C;C;D;C
按要求答题
1.(1)表面积:2×3.14×(6÷2) +3.14 ×6×10÷2+6×10=210.72(m )
体积:3.14×(6÷2) ×10×2=141.3(m )
(2)底面半径:2÷2=1 (cm)
圆柱体积:3.14×12×4=12.56 (cm )
圆锥体积:3.14×12×1.5-3=1.57(cm )
组合图形体积:12.56-1.57=10.99 (cm )
3.14×3 ×6×(2+)=39.564(dm )
3.(1)②③④
(2)3.14×(6÷2) ×(5+12)=480.42(cm )
480.42 cm =480.42 mL
四.解决问题
1.3.14×(0.8÷2) ×14+×3.14×(0.8÷2) ×1.5×2=7.536(cm )
2.(1)6.28÷3.14÷2=1(dm) 3.14×1 ×2+6.28×3=25.12(dm )
(2)3.14×1 ×3=9.42(dm ) 9.42×3÷2=14.13(dm )
3.(1)12.56÷3.14=4(m)3.5-1.5=2(m)3.14×(4÷2) ×2=25.12(m )
×314×(4÷2) ×1.5=628(m )6.28+25.12=31.4(m )
(2)31.4×0.65×70%≈14.29(t)
4. 8×10÷5=16(cm)
5.3.14×(20÷2) ×10-10×10×12=1940(cm )
1940cm =1940 mL=1.94 L
21世纪教育网(www.21cnjy.com)
第三单元复习题
一.填空题。(每空2分,共26分)
1.一个圆柱的侧面积是6.28 cm ,底面直径是2cm,它的高是( )cm。
2.一个圆柱的体积12 cm ,与它等底等高的圆锥的体积是( )cm 。一个圆锥的体积是12cm ,与它等底等高的圆柱的体积是( )cm 。
3.有一款圆柱形的鼓,鼓面直径是4cm,高度是10cm,它的侧面是铝皮,上、下底面蒙的都是牛皮。制作这样一个鼓,共需要铝皮( )cm ,需要牛皮( )cm 。
4.学校礼堂里的柱子可以看作高是5m,底面直径是2m的圆柱。如果每立方米柱子约重3t,那么这根柱子约重( )t。
5.把一个直径是4 cm、高是4 cm的圆柱切拼成一个近似的长方体(如图),这个长方体的体积是( )cm ,长方体的表面积比圆柱的表面积增加了( )cm 。
6.如图,一个帐篷从前面看到的是图1,从上面看到的是图2,这个帐篷的占地面积是( )m ,帐篷里面的空间有( )m 。
7.观察图中的木桶,底面直径是5dm,这个木桶水平放置时最多能盛水
( )L。
8.切割圆柱将一根高5 dm的圆柱形木料沿底面直径垂直切成两部分(如图),这时表面积比原来增加了60 dm 。这根圆柱形木料原来的表面积是( )dm 。
9.有甲、乙两个圆柱形容器,从里面量得它们的底面半径分别是10 cm和5cm,两个容器里的水深分别是10 cm和15 cm。如果将乙容器中的一部分水倒入甲容器,使得两个容器的水面一样高。这时水深为( )cm。
二、选择题。(每题2分,共16分)
1.甲、乙两人分别有一张长12.52cm、宽6.28 cm的纸,用两种不同的方法围成一个圆柱(接头处不重叠),那么围成的圆柱( )。
A.体积一定相等 B.侧面积一定相等 C.表面积一定相等
2.下面图形( )是圆柱的展开图。(单位:cm)
3.把一个底面积是6.28cm 、高是3cm的圆锥形铁块浸没在一个装满水的底面直径是10cm、高是8cm的圆柱形容器中,会溢出( )mL的水。
A.18.84 B.6.28 C.62.8 D.55.52
4.营养学家建议,10岁儿童每天需摄入的水量约为1000 mL,为了达到这个要求,10岁的乐乐每天用底面内直径是6 cm、高是10cm的圆柱形水杯喝水,她每天至少要喝( )杯水。
A.1 B.2 C.3 D.4
5.如图,一个拧紧瓶盖的瓶子里装有一些水,要使瓶子号里水的体积占瓶子容积的,数据设置正确的是( )。
A.h =10 h =17 h =3 B.h =3 h =17 h =10
C.h =6 h =18 h =9 D.h =12 h =25 h =6
6.高和体积分别相等的一个圆柱和一个圆锥,如果圆锥的底面积是15 cm ,那么圆柱的底面积是( )。
A.45 cm B.15cm C.5cm
7.晓峰过生日,好朋友亮亮送给他一个笔筒作为生日礼物(如图)。要求这个笔筒的体积是多少,下面列式正确的是( )。
A.3.14×10 ×16-3.14×10 ×12 B.3.14×(10÷2) ×(16-12)
C.3.14×(10÷2) ×(16+12) D.3.14×(10÷2) ×(16+12)÷2
一根圆柱形木料的底面半径是0.2m,长是3m。将它截成6段,如图所示,这些木料的表面积比原木料的表面积增加了( )m 。
A.1.5072 B.12.56 C.1.256
三.按要求答题(23分)
1.计算下面图形的图(1)表面积和体积,图(2)体积。(单位:cm)(9分)
(1)
(2)
2.计算图形旋转一周得到的立体图形的体积。(单位:dm)(4分)
3.为了测量一个空瓶子的容积,一个学习小组进行了如下实验。(10分)
①测量出整个瓶子的高度是22 cm;
②测量出整个瓶子圆柱部分的内直径是6 cm;
③给瓶子里注入一些水,把瓶子正放时,测量出水的高度是5cm;
④把瓶子倒放时,无水部分是圆柱形,测量出该圆柱的高是12 cm。
(1)要求这个瓶子的容积,上面记录中哪些信息是必须有的 。(填序号)(3分)
(2)请根据选出的信息,求出这个瓶子的容积。(7分)
四.解决问题(35分)
1.为减少小硕妹妹在学校削铅笔的次数,妈妈把她的铅笔两端都削了削(如图)。已知铅笔的直径是0.8 cm,这支削好的铅笔的体积是多少立方厘米 (6分)
2.妈妈用废旧床单给小硕做了一个圆柱形沙袋,不仅缓解学习压力,还增强体质。沙袋底面周长是6.28 dm,高是3 dm(外层厚度忽略不计)。
(1)做这个沙袋用了多少平方分米废旧床单 (损耗忽略不计)(5分)
(2)等积变形一次沙袋底破了,沙子全部流到地板上形成了一个高2 dm的圆锥形沙堆,这个圆锥形沙堆的占地面积是多少平方分米 (5分)
3.如图,粮仓的总高度为3.5m,它的圆柱部分底面周长为12.56m,圆锥部分高为1.5m。(9分)
(1)不考虑粮仓内壁的厚度,这个粮仓的体积是多少 (4分)
(2)每立方米稻谷大约重0.65t。如果稻谷的出米率是70%,一个粮仓的稻谷大约能出多少吨大米 (粮仓装满稻谷,结果保留两位小数)(5分)
4.如果用如图的玻璃杯喝果汁,一壶果汁正好能倒满8杯。现在用如图的塑料杯喝果汁,同样一壶果汁正好能倒满5杯,塑料杯的高是多少 (5分)
5.“铁质零件总是生锈,应该怎么办呢 ”“将零件浸没在防锈油中就可以了。”将一个长10 cm、宽10cm、高12 cm的长方体铁质零件放入一个底面直径是20cm、高20cm的圆柱形容器中浸防锈油,那么容器内至少需要注人多少升防锈油才能完全将零件浸没
答案:
一.填空。
1. 1
2.4;36
3.125.6;25.12
4.47.1
5.5024;16
6.12.56;12.56
7.58.875
8.150.72
9.11
二.选择
B;A;B;D;C;C;D;C
按要求答题
1.(1)表面积:2×3.14×(6÷2) +3.14 ×6×10÷2+6×10=210.72(m )
体积:3.14×(6÷2) ×10×2=141.3(m )
(2)底面半径:2÷2=1 (cm)
圆柱体积:3.14×12×4=12.56 (cm )
圆锥体积:3.14×12×1.5-3=1.57(cm )
组合图形体积:12.56-1.57=10.99 (cm )
3.14×3 ×6×(2+)=39.564(dm )
3.(1)②③④
(2)3.14×(6÷2) ×(5+12)=480.42(cm )
480.42 cm =480.42 mL
四.解决问题
1.3.14×(0.8÷2) ×14+×3.14×(0.8÷2) ×1.5×2=7.536(cm )
2.(1)6.28÷3.14÷2=1(dm) 3.14×1 ×2+6.28×3=25.12(dm )
(2)3.14×1 ×3=9.42(dm ) 9.42×3÷2=14.13(dm )
3.(1)12.56÷3.14=4(m)3.5-1.5=2(m)3.14×(4÷2) ×2=25.12(m )
×314×(4÷2) ×1.5=628(m )6.28+25.12=31.4(m )
(2)31.4×0.65×70%≈14.29(t)
4. 8×10÷5=16(cm)
5.3.14×(20÷2) ×10-10×10×12=1940(cm )
1940cm =1940 mL=1.94 L
21世纪教育网(www.21cnjy.com)
