湘教版(2024)九年级上册数学1.1反比例函数【课件】(共31张PPT)
文档属性
| 名称 | 湘教版(2024)九年级上册数学1.1反比例函数【课件】(共31张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 11.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-14 19:01:16 | ||
图片预览











文档简介
(共31张PPT)
第一章 反比例函数 1.1
反比例函数
湘教版(2024)九年级上册数学课件
01
新课导入
03
课堂小结
02
新课讲解
04
课后作业
目录
新课导入
第一部分
PART 01
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
少年雪地驰骋赛马
新课导入
赛 马
历史最悠久的运动之一.自古至今形式变化甚多,但基本原则都是竞赛速度.
不变
新课导入
在小学,我们已经知道,如果两个量 x,y 满足xy=k(k为常数,k≠0),那么 x,y 就成反比例关系.
不变
速度v与时间t成反比例关系.
新课导入
新课讲解
第二部分
PART 02
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
(1)一群选手在进行全程为3000m的赛马比赛时,各选手的平均速度v(m/s)与所用时间t(s)之间有怎样的关系?并写出它们之间的关系式;
(2)利用(1)的关系式完成下表:
随着时间 t 的变化,平均速度v发生了怎样的变化?
(3)平均速度 v 是所用时间 t 的函数吗?为什么?
所用时间 t /s 121 137 139 143 149
平均速度 v /(m/s) (精确到0.01)
新课讲解
(1)一群选手在进行全程为3000m的赛马比赛时,各选手的平均速度v(m/s)与所用时间t(s)之间有怎样的关系?并写出它们之间的关系式;
我们已经知道,路程与速度、时间之间的关系式为s = vt,因此 .
上述问题中路程s = 3000m,因此选手的平均速度v (m/s)与所用时间t(s)之间的关系式为
新课讲解
(1)一群选手在进行全程为3000m的赛马比赛时,各选手的平均速度v(m/s)与所用时间t(s)之间有怎样的关系?并写出它们之间的关系式;
(2)利用(1)的关系式完成下表:
随着时间 t 的变化,平均速度v发生了怎样的变化?
24.79
21.90
21.58
20.98
20.13
时间 t 越大,平均速度 v 越小;
新课讲解
所用时间 t /s 121 137 139 143 149
平均速度 v /(m/s) (精确到0.01)
(1)一群选手在进行全程为3000m的赛马比赛时,各选手的平均速度v(m/s)与所用时间t(s)之间有怎样的关系?并写出它们之间的关系式;
(2)利用(1)的关系式完成下表:
随着时间 t 的变化,平均速度v发生了怎样的变化?
(3)平均速度 v 是所用时间 t 的函数吗?为什么?
新课讲解
24.79
21.90
21.58
20.98
20.13
所用时间 t /s 121 137 139 143 149
平均速度 v /(m/s) (精确到0.01)
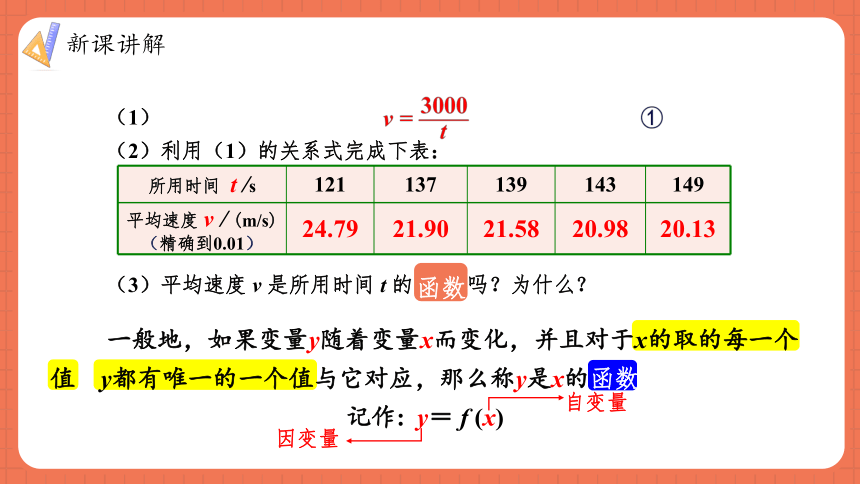
记作: y= f (x)
一般地,如果变量y随着变量x而变化,并且对于x的取的每一个值,y都有唯一的一个值与它对应,那么称y是x的函数.
(1)
(2)利用(1)的关系式完成下表:
(3)平均速度 v 是所用时间 t 的 函数 吗?为什么?
所用时间 t /s 121 137 139 143 149
平均速度 v / (m/s) (精确到0.01) 24.79 21.90 21.58 20.98 20.13
函数
自变量
因变量
新课讲解
(1)
(2)利用(1)的关系式完成下表:
(3)平均速度 v 是所用时间 t 的 函数 吗?为什么?
所用时间 t /(s) 121 137 139 143 149
平均速度 v / (m/s) (精确到0.01) 24.79 21.90 21.58 20.98 20.13
函数
①式表明:当路程 s 一定时,每当 t 取一个值时,v 都有唯一的一个值与它对应,因此平均速度 v 是所用时间 t 的函数.
新课讲解
由于当路程 s 一定时, 平均速度 v 与时间 t 成反比例关系,因此,我们把这样的函数称为反比例函数.
的形式,那么称y是x的反比例函数,其中x是自变量,常数k(k ≠0)称为反比例函数的比例系数.
一般地,如果两个变量 y 与 x 的关系可以表示成
(k为常数,k≠0)
或
(k为常数,k≠0)
x≠0
(所有非零实数)
新课讲解
=
一般地,如果两个变量 y 与 x 的关系可以表示成
(k为常数,k≠0)
或
——
3000
v
t
①
3000
比例系数
表明 是 的反比例函数.
速度 v
时间 t
t>0
(k为常数,k≠0)
x≠0
(所有非零实数)
v>0
新课讲解
的形式,那么称y是x的反比例函数,其中x是自变量,常数k(k ≠0)称为反比例函数的比例系数.
如图1-1,已知菱形ABCD的面积180,设它的两条对角线AC,BD的长分别为x,y.写出变量y与x之间的函数表达式,并指出它是什么函数.
例
解:因为菱形的面积等于两条对角线长乘积的一半,
所以xy=360(定值),即y与x成反比例关系.
因此,当菱形的面积一定时,它的一条对角线长y是另一条对角线长x的反比例函数.
所以
所以
图1-1
新课讲解
[选自教材P3 练习 第1题]
1.下列函数是不是反比例函数?若是,请写出它的比例系数.
(1)是,比例系数是3;
(2)不是;
(3)是,比例系数是 ;
(4)是,比例系数是 .
课堂练习
[选自教材P3 练习 第2题]
2.下列问题中,变量间的对应关系可以用怎样的函数表达式表示?
(1)已知矩形的面积为120cm2,矩形的长y(cm)随宽x(cm)的变化而变化;
(2)用 100 元买某种水果,水果的单价 x(元/kg)与购买的数量 y(kg)之间的对应关系.
课堂练习
1. 下列函数是不是反比例函数?若是,请写出它的比例系数.
[选自教材P4 习题1.1 A组 第1题]
是,比例系数是2;
是,比例系数是1;
是,比例系数是﹣2;
是,比例系数是 .
课堂练习
2. 已知某空游泳池的容积为270 m3,用恰当的函数表达式来表示进水速度v(m3/h)与注满该游泳池所需时间t(h)之间的关系.
[选自教材P4 习题1.1 A组 第2题]
解:
课堂练习
[选自教材P4 习题1.1 A组 第3题]
(2)求当x=﹣3时的函数的值;
(3)求当y=﹣2时自变量x的值.
3.已知反比例函数
(1)写出这个函数的比例系数和自变量的取值范围;
解:(1)比例系数是﹣6,自变量的取值范围是x≠0;
(2)
(3)
课堂练习
[选自教材P4 习题1.1 A组 第4题]
4.(1)根据函数表达式填写下表:
x ﹣4 ﹣3 ﹣2 ﹣1 1 2 3 4
﹣2
﹣4
﹣8
8
4
2
(2)观察上表,由此猜测,当x取正数时,随着x的增大,y的值是怎样变化的?当x取负数时,随着x的增大,y的值是怎样变化的?
(2)当x取正数时,随着x的增大,y的值减小;
当x取负数时,随着x的增大,y的值减小.
课堂练习
5.分别写出下列函数的表达式,并指出其中哪些是正比例函数,哪些是反比例函数.
(1)当速度v=3 m/s时,路程s(m)关于时间t(s)的函数;
(2)当购买了300kW·h电时,每天的用电量n(kW·h)关于可使用天数 m(天)的函数;
(3)当圆柱体的体积V=100 cm3时,其底面积S(cm2)关于高h(cm)的函数.
解:(1)s=3t,是正比例函数;
(2) 是反比例函数;
(3) 是反比例函数;
[选自教材P4 习题1.1 B组 第5题]
课堂练习
6.根据下列式子,写出y关于x的函数表达式,并指出其中哪些是一次函数,哪些是反比例函数.
[选自教材P4 习题1.1 B组 第6题]
课堂练习
1.一张矩形纸的面积为100cm2 ,相邻两条边长分别为x cm和
y cm,y是x的反比例函数吗?_______ (填“是”或“否”).
是
课堂练习
2.(2011 ·扬州)某反比例函数的图象经过点(-1,6),则
下列各点中函数图象也经过的点是( )
A.(-3,2) B.(3,2)
C.(2,3) D.(6,1)
A
课堂练习
课堂小结
第三部分
PART 03
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
的形式,那么称y是x的反比例函数,其中x是自变量,常数k(k ≠0)称为反比例函数的比例系数.
一般地,如果两个变量 y 与 x 的关系可以表示成
(k为常数,k≠0)
或
(k为常数,k≠0)
x≠0
(所有非零实数)
课堂小结
课后作业
第四部分
PART 04
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
1.从课后习题中选取;
2.完成练习册本课时的习题.
课后作业
第一章 反比例函数 1.1
反比例函数
湘教版(2024)九年级上册数学课件
第一章 反比例函数 1.1
反比例函数
湘教版(2024)九年级上册数学课件
01
新课导入
03
课堂小结
02
新课讲解
04
课后作业
目录
新课导入
第一部分
PART 01
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
少年雪地驰骋赛马
新课导入
赛 马
历史最悠久的运动之一.自古至今形式变化甚多,但基本原则都是竞赛速度.
不变
新课导入
在小学,我们已经知道,如果两个量 x,y 满足xy=k(k为常数,k≠0),那么 x,y 就成反比例关系.
不变
速度v与时间t成反比例关系.
新课导入
新课讲解
第二部分
PART 02
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
(1)一群选手在进行全程为3000m的赛马比赛时,各选手的平均速度v(m/s)与所用时间t(s)之间有怎样的关系?并写出它们之间的关系式;
(2)利用(1)的关系式完成下表:
随着时间 t 的变化,平均速度v发生了怎样的变化?
(3)平均速度 v 是所用时间 t 的函数吗?为什么?
所用时间 t /s 121 137 139 143 149
平均速度 v /(m/s) (精确到0.01)
新课讲解
(1)一群选手在进行全程为3000m的赛马比赛时,各选手的平均速度v(m/s)与所用时间t(s)之间有怎样的关系?并写出它们之间的关系式;
我们已经知道,路程与速度、时间之间的关系式为s = vt,因此 .
上述问题中路程s = 3000m,因此选手的平均速度v (m/s)与所用时间t(s)之间的关系式为
新课讲解
(1)一群选手在进行全程为3000m的赛马比赛时,各选手的平均速度v(m/s)与所用时间t(s)之间有怎样的关系?并写出它们之间的关系式;
(2)利用(1)的关系式完成下表:
随着时间 t 的变化,平均速度v发生了怎样的变化?
24.79
21.90
21.58
20.98
20.13
时间 t 越大,平均速度 v 越小;
新课讲解
所用时间 t /s 121 137 139 143 149
平均速度 v /(m/s) (精确到0.01)
(1)一群选手在进行全程为3000m的赛马比赛时,各选手的平均速度v(m/s)与所用时间t(s)之间有怎样的关系?并写出它们之间的关系式;
(2)利用(1)的关系式完成下表:
随着时间 t 的变化,平均速度v发生了怎样的变化?
(3)平均速度 v 是所用时间 t 的函数吗?为什么?
新课讲解
24.79
21.90
21.58
20.98
20.13
所用时间 t /s 121 137 139 143 149
平均速度 v /(m/s) (精确到0.01)
记作: y= f (x)
一般地,如果变量y随着变量x而变化,并且对于x的取的每一个值,y都有唯一的一个值与它对应,那么称y是x的函数.
(1)
(2)利用(1)的关系式完成下表:
(3)平均速度 v 是所用时间 t 的 函数 吗?为什么?
所用时间 t /s 121 137 139 143 149
平均速度 v / (m/s) (精确到0.01) 24.79 21.90 21.58 20.98 20.13
函数
自变量
因变量
新课讲解
(1)
(2)利用(1)的关系式完成下表:
(3)平均速度 v 是所用时间 t 的 函数 吗?为什么?
所用时间 t /(s) 121 137 139 143 149
平均速度 v / (m/s) (精确到0.01) 24.79 21.90 21.58 20.98 20.13
函数
①式表明:当路程 s 一定时,每当 t 取一个值时,v 都有唯一的一个值与它对应,因此平均速度 v 是所用时间 t 的函数.
新课讲解
由于当路程 s 一定时, 平均速度 v 与时间 t 成反比例关系,因此,我们把这样的函数称为反比例函数.
的形式,那么称y是x的反比例函数,其中x是自变量,常数k(k ≠0)称为反比例函数的比例系数.
一般地,如果两个变量 y 与 x 的关系可以表示成
(k为常数,k≠0)
或
(k为常数,k≠0)
x≠0
(所有非零实数)
新课讲解
=
一般地,如果两个变量 y 与 x 的关系可以表示成
(k为常数,k≠0)
或
——
3000
v
t
①
3000
比例系数
表明 是 的反比例函数.
速度 v
时间 t
t>0
(k为常数,k≠0)
x≠0
(所有非零实数)
v>0
新课讲解
的形式,那么称y是x的反比例函数,其中x是自变量,常数k(k ≠0)称为反比例函数的比例系数.
如图1-1,已知菱形ABCD的面积180,设它的两条对角线AC,BD的长分别为x,y.写出变量y与x之间的函数表达式,并指出它是什么函数.
例
解:因为菱形的面积等于两条对角线长乘积的一半,
所以xy=360(定值),即y与x成反比例关系.
因此,当菱形的面积一定时,它的一条对角线长y是另一条对角线长x的反比例函数.
所以
所以
图1-1
新课讲解
[选自教材P3 练习 第1题]
1.下列函数是不是反比例函数?若是,请写出它的比例系数.
(1)是,比例系数是3;
(2)不是;
(3)是,比例系数是 ;
(4)是,比例系数是 .
课堂练习
[选自教材P3 练习 第2题]
2.下列问题中,变量间的对应关系可以用怎样的函数表达式表示?
(1)已知矩形的面积为120cm2,矩形的长y(cm)随宽x(cm)的变化而变化;
(2)用 100 元买某种水果,水果的单价 x(元/kg)与购买的数量 y(kg)之间的对应关系.
课堂练习
1. 下列函数是不是反比例函数?若是,请写出它的比例系数.
[选自教材P4 习题1.1 A组 第1题]
是,比例系数是2;
是,比例系数是1;
是,比例系数是﹣2;
是,比例系数是 .
课堂练习
2. 已知某空游泳池的容积为270 m3,用恰当的函数表达式来表示进水速度v(m3/h)与注满该游泳池所需时间t(h)之间的关系.
[选自教材P4 习题1.1 A组 第2题]
解:
课堂练习
[选自教材P4 习题1.1 A组 第3题]
(2)求当x=﹣3时的函数的值;
(3)求当y=﹣2时自变量x的值.
3.已知反比例函数
(1)写出这个函数的比例系数和自变量的取值范围;
解:(1)比例系数是﹣6,自变量的取值范围是x≠0;
(2)
(3)
课堂练习
[选自教材P4 习题1.1 A组 第4题]
4.(1)根据函数表达式填写下表:
x ﹣4 ﹣3 ﹣2 ﹣1 1 2 3 4
﹣2
﹣4
﹣8
8
4
2
(2)观察上表,由此猜测,当x取正数时,随着x的增大,y的值是怎样变化的?当x取负数时,随着x的增大,y的值是怎样变化的?
(2)当x取正数时,随着x的增大,y的值减小;
当x取负数时,随着x的增大,y的值减小.
课堂练习
5.分别写出下列函数的表达式,并指出其中哪些是正比例函数,哪些是反比例函数.
(1)当速度v=3 m/s时,路程s(m)关于时间t(s)的函数;
(2)当购买了300kW·h电时,每天的用电量n(kW·h)关于可使用天数 m(天)的函数;
(3)当圆柱体的体积V=100 cm3时,其底面积S(cm2)关于高h(cm)的函数.
解:(1)s=3t,是正比例函数;
(2) 是反比例函数;
(3) 是反比例函数;
[选自教材P4 习题1.1 B组 第5题]
课堂练习
6.根据下列式子,写出y关于x的函数表达式,并指出其中哪些是一次函数,哪些是反比例函数.
[选自教材P4 习题1.1 B组 第6题]
课堂练习
1.一张矩形纸的面积为100cm2 ,相邻两条边长分别为x cm和
y cm,y是x的反比例函数吗?_______ (填“是”或“否”).
是
课堂练习
2.(2011 ·扬州)某反比例函数的图象经过点(-1,6),则
下列各点中函数图象也经过的点是( )
A.(-3,2) B.(3,2)
C.(2,3) D.(6,1)
A
课堂练习
课堂小结
第三部分
PART 03
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
的形式,那么称y是x的反比例函数,其中x是自变量,常数k(k ≠0)称为反比例函数的比例系数.
一般地,如果两个变量 y 与 x 的关系可以表示成
(k为常数,k≠0)
或
(k为常数,k≠0)
x≠0
(所有非零实数)
课堂小结
课后作业
第四部分
PART 04
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
1.从课后习题中选取;
2.完成练习册本课时的习题.
课后作业
第一章 反比例函数 1.1
反比例函数
湘教版(2024)九年级上册数学课件
同课章节目录
- 第1章 反比例函数
- 1.1 反比例函数
- 1.2 反比例函数的图像与性质
- 1.3 反比例函数的应用
- 第2章 一元二次方程
- 2.1 一元二次方程
- 2.2 一元二次方程的解法
- 2.3 一元二次方程根的判别式
- 2.4 一元二次方程根与系数的关系
- 2.5 一元二次方程的应用
- 第3章 图形的相似
- 3.1 比例线段
- 3.2 平行线分线段成比例
- 3.3 相似图形
- 3.4 相似三角形的判定与性质
- 3.5 相似三角形的应用
- 3.6 位似
- 第4章 锐角三角函数
- 4.1 正弦和余弦
- 4.2 正切
- 4.3 解直角三角形
- 4.4 解直接三角形的应用
- 第5章 用样本推断总体
- 5.1 总体平均数与方差的估计
- 5.2 统计的简单应用
