湘教版(2024)九年级下册数学 2.2.1圆心角 课件(共21张PPT)
文档属性
| 名称 | 湘教版(2024)九年级下册数学 2.2.1圆心角 课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 10.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-15 07:59:33 | ||
图片预览





文档简介
(共21张PPT)
第二章 圆 2.2.1
圆心角
湘教版(2024)九年级下册数学课件
01
新课导入
03
课堂练习
02
新课讲解
04
课堂小结
目录
新课导入
第一部分
PART 01
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
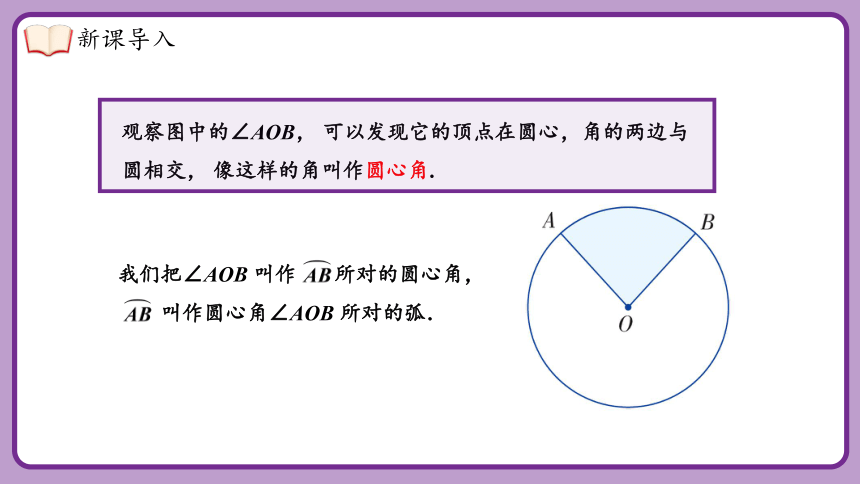
观察图中的∠AOB, 可以发现它的顶点在圆心,角的两边与圆相交, 像这样的角叫作圆心角.
我们把∠AOB 叫作 所对的圆心角,
叫作圆心角∠AOB 所对的弧.
新课导入
新课讲解
第二部分
PART 02
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
在生活中,我们常遇到圆心角,如飞镖靶中有圆心角,还有手表的时针与分针所成的角等也是圆心角.
新课讲解
判断下列各图中的角是不是圆心角,并说明理由.
【对应练习】
新课讲解
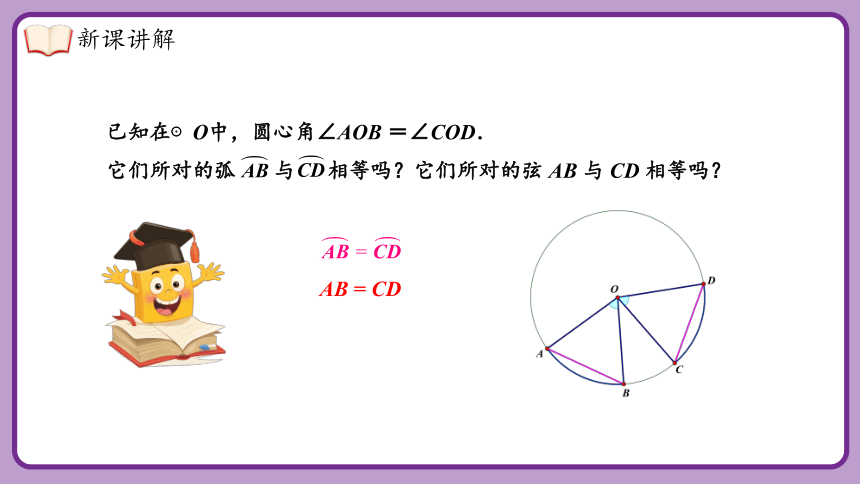
已知在⊙O中,圆心角∠AOB =∠COD.
它们所对的弧 与 相等吗?它们所对的弦 AB 与 CD 相等吗?
AB = CD
新课讲解
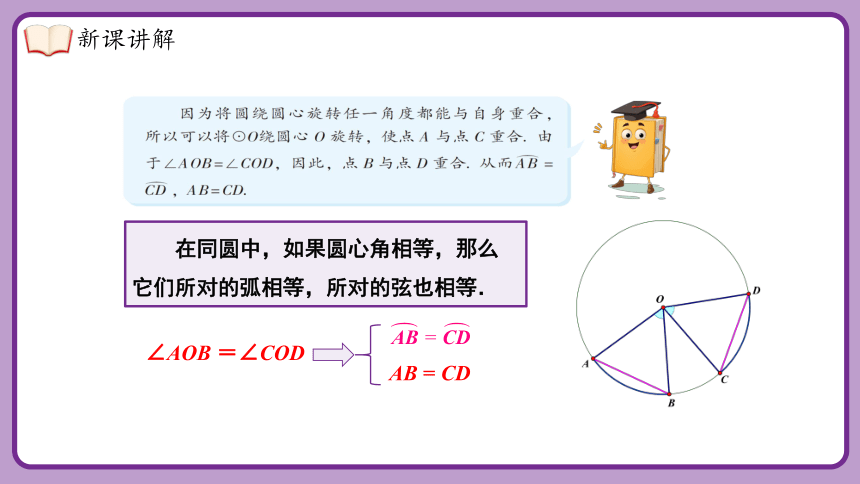
在同圆中,如果圆心角相等,那么它们所对的弧相等,所对的弦也相等.
∠AOB =∠COD
AB = CD
新课讲解
在同圆或等圆中,如果弧相等,那么它们所对的圆心角相等吗?所对的弦相等吗?
在同圆或等圆中,如果弦相等,那么它们所对的圆心角相等吗?所对的弧相等吗?
在同圆或等圆中,如果两个圆心角、两条弧和两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.
新课讲解
如图,等边△ABC 的顶点 A,B,C 在⊙O 上,求圆心角 ∠AOB 的度数.
解 ∵ △ABC 为等边三角形,
∴ AB = BC = AC.
∴ ∠AOB =∠BOC =∠COA .
又∵ ∠AOB +∠BOC +∠COA = 360°,
∴ ∠AOB = (∠AOB+∠BOC+∠COA)
= × 360 ° = 120° .
【教材P48页】
新课讲解
1.在⊙O中,已知∠AOB = 40°, ,求∠COD的度数.
解 ∵
∴∠COD = ∠AOB = 40°
【教材P48页】
新课讲解
2. 如图,在⊙O中,AB 是直径,∠AOE = 60°,点 C,D 是 的三等分点,求∠COE 的度数.
解 ∵ ∠AOE = 60°
∴∠BOE = 120°
又∵点 C,D 是 的三等分点
∴∠BOC = ∠COD = ∠DOE = 40°
∴∠COE = 80°
【教材P48页】
新课讲解
课堂练习
第三部分
PART 03
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
如图, 在☉O 中, ,∠A=30°,则∠B 的度数为( )
A. 150°
B. 75°
C. 60°
D. 15°
B
课堂练习
2. 如图,在☉O 中,若 C 是 的中点, ∠OAB=50°,
则∠BOC 的度数为( )
A. 40°
B. 45°
C. 50°
D. 60°
A
课堂练习
3. 如图, AB 是 ☉O 的直径, BC , CD , DA 是☉O 的弦,
且 BC = CD = DA , 则∠BCD 的度数为( )
A. 100° B. 110° C. 120° D.135°
C
课堂练习
课堂小结
第四部分
PART 04
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
在同圆或等圆中,如果圆心角相等,那么它们所对的弧相等,所对的弦也相等.
∠AOB =∠COD
AB = CD
课堂小结
在同圆或等圆中,如果两个圆心角、两条弧和两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.
∠AOB =∠COD
AB = CD
∠AOB =∠COD
AB = CD
AB = CD
∠AOB =∠COD
课堂小结
第二章 圆 2.2.1
圆心角
湘教版(2024)九年级下册数学课件
第二章 圆 2.2.1
圆心角
湘教版(2024)九年级下册数学课件
01
新课导入
03
课堂练习
02
新课讲解
04
课堂小结
目录
新课导入
第一部分
PART 01
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
观察图中的∠AOB, 可以发现它的顶点在圆心,角的两边与圆相交, 像这样的角叫作圆心角.
我们把∠AOB 叫作 所对的圆心角,
叫作圆心角∠AOB 所对的弧.
新课导入
新课讲解
第二部分
PART 02
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
在生活中,我们常遇到圆心角,如飞镖靶中有圆心角,还有手表的时针与分针所成的角等也是圆心角.
新课讲解
判断下列各图中的角是不是圆心角,并说明理由.
【对应练习】
新课讲解
已知在⊙O中,圆心角∠AOB =∠COD.
它们所对的弧 与 相等吗?它们所对的弦 AB 与 CD 相等吗?
AB = CD
新课讲解
在同圆中,如果圆心角相等,那么它们所对的弧相等,所对的弦也相等.
∠AOB =∠COD
AB = CD
新课讲解
在同圆或等圆中,如果弧相等,那么它们所对的圆心角相等吗?所对的弦相等吗?
在同圆或等圆中,如果弦相等,那么它们所对的圆心角相等吗?所对的弧相等吗?
在同圆或等圆中,如果两个圆心角、两条弧和两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.
新课讲解
如图,等边△ABC 的顶点 A,B,C 在⊙O 上,求圆心角 ∠AOB 的度数.
解 ∵ △ABC 为等边三角形,
∴ AB = BC = AC.
∴ ∠AOB =∠BOC =∠COA .
又∵ ∠AOB +∠BOC +∠COA = 360°,
∴ ∠AOB = (∠AOB+∠BOC+∠COA)
= × 360 ° = 120° .
【教材P48页】
新课讲解
1.在⊙O中,已知∠AOB = 40°, ,求∠COD的度数.
解 ∵
∴∠COD = ∠AOB = 40°
【教材P48页】
新课讲解
2. 如图,在⊙O中,AB 是直径,∠AOE = 60°,点 C,D 是 的三等分点,求∠COE 的度数.
解 ∵ ∠AOE = 60°
∴∠BOE = 120°
又∵点 C,D 是 的三等分点
∴∠BOC = ∠COD = ∠DOE = 40°
∴∠COE = 80°
【教材P48页】
新课讲解
课堂练习
第三部分
PART 03
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
如图, 在☉O 中, ,∠A=30°,则∠B 的度数为( )
A. 150°
B. 75°
C. 60°
D. 15°
B
课堂练习
2. 如图,在☉O 中,若 C 是 的中点, ∠OAB=50°,
则∠BOC 的度数为( )
A. 40°
B. 45°
C. 50°
D. 60°
A
课堂练习
3. 如图, AB 是 ☉O 的直径, BC , CD , DA 是☉O 的弦,
且 BC = CD = DA , 则∠BCD 的度数为( )
A. 100° B. 110° C. 120° D.135°
C
课堂练习
课堂小结
第四部分
PART 04
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
在同圆或等圆中,如果圆心角相等,那么它们所对的弧相等,所对的弦也相等.
∠AOB =∠COD
AB = CD
课堂小结
在同圆或等圆中,如果两个圆心角、两条弧和两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等.
∠AOB =∠COD
AB = CD
∠AOB =∠COD
AB = CD
AB = CD
∠AOB =∠COD
课堂小结
第二章 圆 2.2.1
圆心角
湘教版(2024)九年级下册数学课件
