湘教版(2024)九年级下册数学 2.5.2.2 切线的性质 课件(共18张ppt)
文档属性
| 名称 | 湘教版(2024)九年级下册数学 2.5.2.2 切线的性质 课件(共18张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-15 00:00:00 | ||
图片预览




文档简介
(共18张PPT)
第二章 圆 2.5.2
圆的切线
2.5.2.2 切线的性质
01
新课导入
03
课堂练习
02
新课讲解
04
课堂小结
目录
新课导入
第一部分
PART 01
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
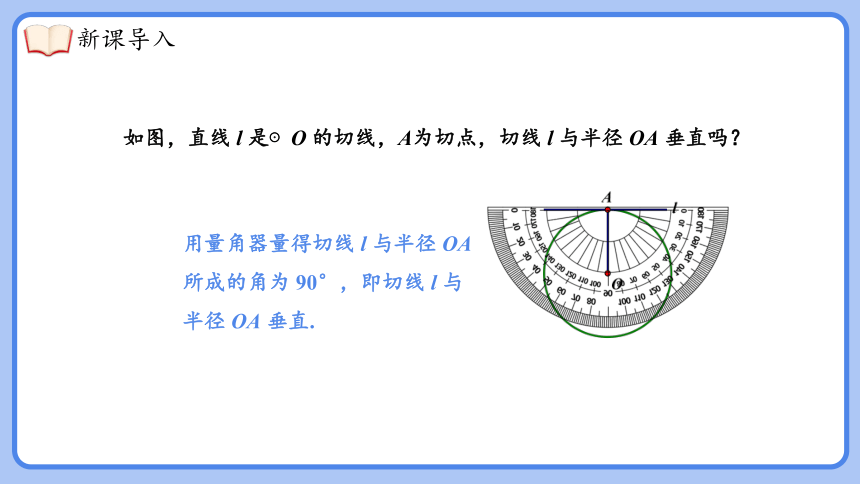
用量角器量得切线 l 与半径 OA 所成的角为 90°,即切线 l 与半径 OA 垂直.
如图,直线 l 是⊙O 的切线,A为切点,切线 l 与半径 OA 垂直吗?
新课导入
如图,直线 l 是⊙O 的切线,A为切点,切线 l 与半径 OA 垂直吗?
下面我们用反证法来证明这个结论.
假设直线 l 与半径 OA 不垂直.
过圆心 O 作 OB ⊥ l 于点 B.
由于垂线段最短, 可得 OB < OA,
那么圆心 O 到直线 l 的距离小于半径,
即直线 l 与⊙O 相交. 这与已知直线 l 是 ⊙O 的切线相矛盾.
因此直线 l ⊥ OA.
新课导入
新课讲解
第二部分
PART 02
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
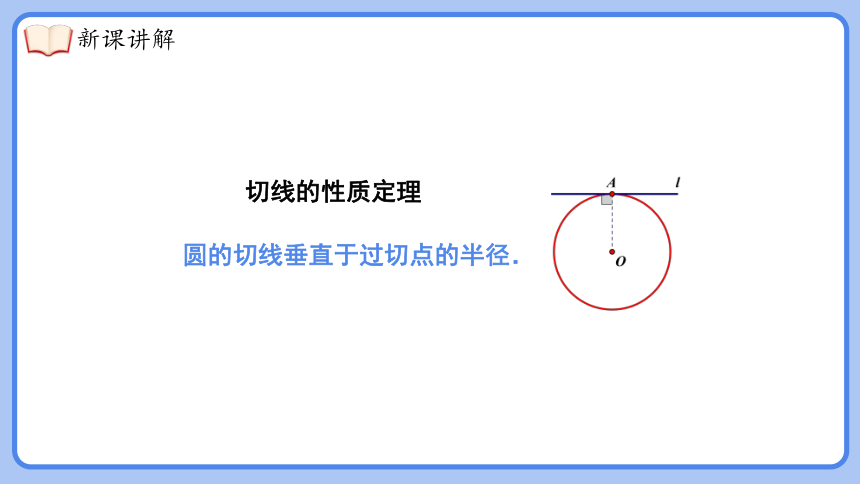
切线的性质定理
圆的切线垂直于过切点的半径.
新课讲解
对于任意一条直线,如果具备下列条件中的两个,就可以推出第三个结论:
(1)垂直于切线;
(2)经过切点;
(3)经过圆心.
新课讲解
如图,AB 是⊙O 的直径,C 为⊙O 上一点,BD 和过点 C 的切线 CD 垂直,垂足为D.求证:BC 平分∠ABD.
证明: 连接 OC.
∵ CD 是⊙O 的切线,
∴ OC⊥CD .
又∵ BD⊥CD ,
∴ BD∥OC .
【教材P68页】
∴ ∠1 =∠2 .
又OC = OB ,
∴ ∠1 =∠3 .
∴ ∠2 =∠3 ,
即 BC 平分∠ABD.
新课讲解
证明:经过直径两端点的切线互相平行.
已知:如图,AB 是⊙O 的直径, l1,l2 分别是经过点 A,B 的切线.
求证:l1∥l2 .
证明: ∵ OA 是⊙O 的半径,
l1是过点 A 的切线,
∴ l1⊥OA. 同理 l2 ⊥ OB.
∴ l1⊥ AB,且 l2⊥ AB.
∴ l1∥l2 .
【教材P68页】
新课讲解
如图,两个同心圆的圆心是 O,大圆的弦 AB 所在直线 切小圆于点 C.
求证:点 C 是线段 AB 的中点.
证明:连接 OC,OA,OB.
∵ AB 是小圆的切线,切点为 C,
∴ OC⊥AB.
又∵在大圆中,OA=OB,
∴ 点 C 是线段 AB 的中点.
【教材P69页】
新课讲解
2. 如图,在⊙O 中,AB 为直径,AD 为弦,过点 B 的切线
与 AD 的延长线交于点 C,且 AD = DC. 求∠ABD 的度数.
【教材P69页】
解: ∵ CB 是⊙O 的切线, 切点为 B,
∴ AB⊥BC.
∵ AB为⊙O 的直径,∴ ∠ADB = 90°.
又∵ AD=DC,
∴ 在Rt△ABC 中, DB=AD=DC,
∴ ∠ABD = 45°.
新课讲解
课堂练习
第三部分
PART 03
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
1. 如图, 已知直线 AD 是☉O 的切线 , A 为切点 , OD 交
☉O 于点 B , 点 C 在☉O 上 , 且∠ODA =36°, 则
∠ACB 的度数为( )
A. 54° B. 36°
C. 30° D. 27°
D
课堂练习
2. (分类讨论题)直线 AB 与☉O 相切于点 B , C 是☉O 与 OA 的交点 , D 是☉O 上的动点(点 D 与点 B, C 不重合).
若∠A= 40°, 则∠BDC 的度数是( )
A. 25°或 155° B. 50°或 155°
C. 25°或 130° D. 50°或 130°
A
课堂练习
3. 如图 , 直线 AB 与☉O 相切于点 A , AC , CD 是☉O 的两条弦 , 且 CD ∥AB.若☉O 的半径为 , CD = 4 , 则弦AC 的长为__________.
A
O
C
D
B
课堂练习
课堂小结
第四部分
PART 04
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
切线的性质有如下几个:
(1) 切线和圆只有一个公共点;
(2) 切线和圆心的距离等于圆的半径;
(3) 切线垂直于过切点的半径.
课堂小结
第二章 圆 2.5.2
圆的切线
2.5.2.2 切线的性质
01
新课导入
03
课堂练习
02
新课讲解
04
课堂小结
目录
新课导入
第一部分
PART 01
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
用量角器量得切线 l 与半径 OA 所成的角为 90°,即切线 l 与半径 OA 垂直.
如图,直线 l 是⊙O 的切线,A为切点,切线 l 与半径 OA 垂直吗?
新课导入
如图,直线 l 是⊙O 的切线,A为切点,切线 l 与半径 OA 垂直吗?
下面我们用反证法来证明这个结论.
假设直线 l 与半径 OA 不垂直.
过圆心 O 作 OB ⊥ l 于点 B.
由于垂线段最短, 可得 OB < OA,
那么圆心 O 到直线 l 的距离小于半径,
即直线 l 与⊙O 相交. 这与已知直线 l 是 ⊙O 的切线相矛盾.
因此直线 l ⊥ OA.
新课导入
新课讲解
第二部分
PART 02
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
切线的性质定理
圆的切线垂直于过切点的半径.
新课讲解
对于任意一条直线,如果具备下列条件中的两个,就可以推出第三个结论:
(1)垂直于切线;
(2)经过切点;
(3)经过圆心.
新课讲解
如图,AB 是⊙O 的直径,C 为⊙O 上一点,BD 和过点 C 的切线 CD 垂直,垂足为D.求证:BC 平分∠ABD.
证明: 连接 OC.
∵ CD 是⊙O 的切线,
∴ OC⊥CD .
又∵ BD⊥CD ,
∴ BD∥OC .
【教材P68页】
∴ ∠1 =∠2 .
又OC = OB ,
∴ ∠1 =∠3 .
∴ ∠2 =∠3 ,
即 BC 平分∠ABD.
新课讲解
证明:经过直径两端点的切线互相平行.
已知:如图,AB 是⊙O 的直径, l1,l2 分别是经过点 A,B 的切线.
求证:l1∥l2 .
证明: ∵ OA 是⊙O 的半径,
l1是过点 A 的切线,
∴ l1⊥OA. 同理 l2 ⊥ OB.
∴ l1⊥ AB,且 l2⊥ AB.
∴ l1∥l2 .
【教材P68页】
新课讲解
如图,两个同心圆的圆心是 O,大圆的弦 AB 所在直线 切小圆于点 C.
求证:点 C 是线段 AB 的中点.
证明:连接 OC,OA,OB.
∵ AB 是小圆的切线,切点为 C,
∴ OC⊥AB.
又∵在大圆中,OA=OB,
∴ 点 C 是线段 AB 的中点.
【教材P69页】
新课讲解
2. 如图,在⊙O 中,AB 为直径,AD 为弦,过点 B 的切线
与 AD 的延长线交于点 C,且 AD = DC. 求∠ABD 的度数.
【教材P69页】
解: ∵ CB 是⊙O 的切线, 切点为 B,
∴ AB⊥BC.
∵ AB为⊙O 的直径,∴ ∠ADB = 90°.
又∵ AD=DC,
∴ 在Rt△ABC 中, DB=AD=DC,
∴ ∠ABD = 45°.
新课讲解
课堂练习
第三部分
PART 03
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
1. 如图, 已知直线 AD 是☉O 的切线 , A 为切点 , OD 交
☉O 于点 B , 点 C 在☉O 上 , 且∠ODA =36°, 则
∠ACB 的度数为( )
A. 54° B. 36°
C. 30° D. 27°
D
课堂练习
2. (分类讨论题)直线 AB 与☉O 相切于点 B , C 是☉O 与 OA 的交点 , D 是☉O 上的动点(点 D 与点 B, C 不重合).
若∠A= 40°, 则∠BDC 的度数是( )
A. 25°或 155° B. 50°或 155°
C. 25°或 130° D. 50°或 130°
A
课堂练习
3. 如图 , 直线 AB 与☉O 相切于点 A , AC , CD 是☉O 的两条弦 , 且 CD ∥AB.若☉O 的半径为 , CD = 4 , 则弦AC 的长为__________.
A
O
C
D
B
课堂练习
课堂小结
第四部分
PART 04
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
切线的性质有如下几个:
(1) 切线和圆只有一个公共点;
(2) 切线和圆心的距离等于圆的半径;
(3) 切线垂直于过切点的半径.
课堂小结
