湘教版(2024)九年级下册数学 2.7 正多边形与圆 课件(共22张PPT)
文档属性
| 名称 | 湘教版(2024)九年级下册数学 2.7 正多边形与圆 课件(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-15 14:06:51 | ||
图片预览




文档简介
(共22张PPT)
第二章 圆 2.7
正多边形与圆
01
新课导入
03
课堂练习
02
新课讲解
04
课堂小结
目录
新课导入
第一部分
PART 01
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
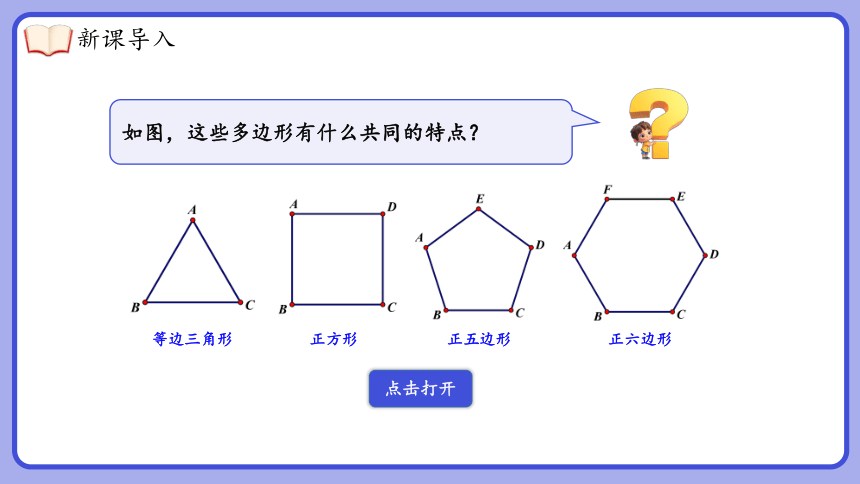
如图,这些多边形有什么共同的特点?
等边三角形
正方形
正五边形
正六边形
点击打开
新课导入
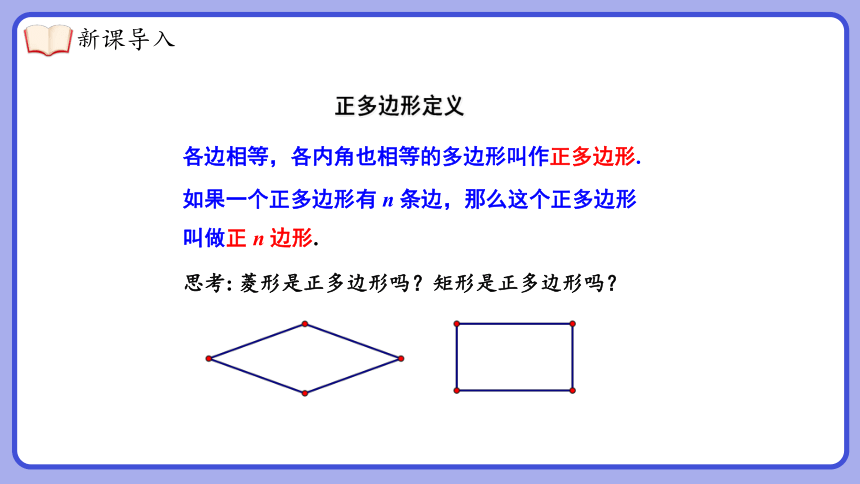
各边相等,各内角也相等的多边形叫作正多边形.
正多边形定义
如果一个正多边形有 n 条边,那么这个正多边形
叫做正 n 边形.
思考: 菱形是正多边形吗?矩形是正多边形吗?
新课导入
新课讲解
第二部分
PART 02
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
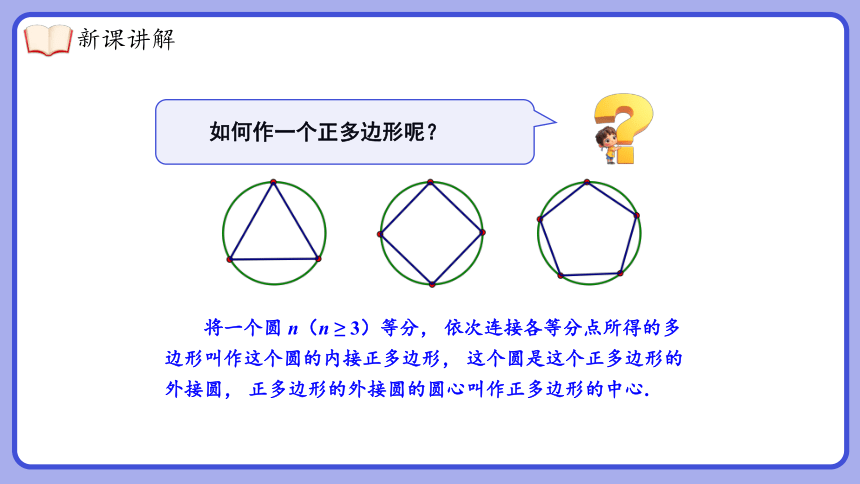
如何作一个正多边形呢?
新课讲解
如何作一个正多边形呢?
将一个圆 n(n ≥ 3)等分, 依次连接各等分点所得的多边形叫作这个圆的内接正多边形, 这个圆是这个正多边形的外接圆, 正多边形的外接圆的圆心叫作正多边形的中心.
新课讲解
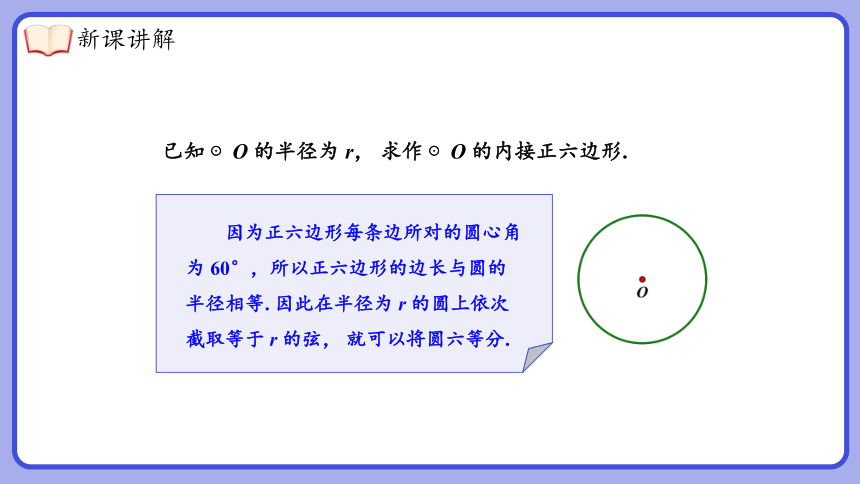
已知 ⊙O 的半径为 r, 求作 ⊙O 的内接正六边形.
因为正六边形每条边所对的圆心角为 60°,所以正六边形的边长与圆的半径相等. 因此在半径为 r 的圆上依次截取等于 r 的弦, 就可以将圆六等分.
新课讲解
已知 ⊙O 的半径为 r, 求作 ⊙O 的内接正六边形.
作法:(1)作⊙O 的任意直径 BE,分别以 B,E 为圆心,以 r 为半径作弧,与⊙O分别相交于点 A,C 和 F,D.
(2) 依次连接 AB,BC,CD,DE,EF, FA,则六边形 ABCDEF 就是所求作的⊙O 的内接正六边形.
新课讲解
如图,已知⊙O 的半径为 r,求作⊙O 的内接正方形.
分析 作两条互相垂直的直径,就可以将 ⊙O 四等分.
作法:(1)作直径 AC与 BD,使 AC ⊥ BD.
(2) 依次连接 AB,BC,CD,DA,则四边形 ABCD 就是所求作的 ⊙O 的内接正方形.
【教材P84页】
新课讲解
在生产设计中,人们经常会遇到等分圆的问题. 例如设计剪纸、齿轮、汽车轮毂等就是通过等分圆而得到的.
新课讲解
观察图中的正多边形,哪些是轴对称图形?哪些是中心对称图形?如果是轴对称图形,画出其对称轴; 如果是中心对称图形,找出其对称中心.
新课讲解
正多边形都是 图形,一个正 n 边形共有 条对称轴,每条对称轴都通过 n 边形的 .
轴对称
n
中心
边数是偶数的正多边形还是 ,它的中心就是对称中心.
中心对称图形
新课讲解
已知⊙O 的半径为 2 cm, 求作⊙O 的内接正方形和内接正六边形.
【教材P85页】
新课讲解
2. 许多图案设计都和圆有关,观察下图,请利用等分圆
的方法设计一幅图案.
【教材P86页】
新课讲解
课堂练习
第三部分
PART 03
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
1. 对于一个正多边形,下列四个命题中, 错误的是( )
A. 正多边形是轴对称图形, 每条边的垂直平分线是它的对称轴
B. 正多边形是中心对称图形, 正多边形的中心是它的对称中心
C. 正多边形每一个外角都等于正多边形的中心角
D. 正多边形每一个内角都与正多边形的中心角互补
B
课堂练习
2. 如图, 平面上两个正方形与正五边形都有一条公共边,
则∠α 等于( )
A. 45° B. 56°
C. 60° D. 72°
D
课堂练习
3. (贵阳中考)如图, 正六边形 ABCDEF 内接于☉O,
☉O 的半径为 6, OM ⊥ BC 于点 M , 则 OM 的长为
_______.
课堂练习
课堂小结
第四部分
PART 04
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
1.什么是正多边形?
2.如何画正多边形?
课堂小结
第二章 圆 2.7
正多边形与圆
01
新课导入
03
课堂练习
02
新课讲解
04
课堂小结
目录
新课导入
第一部分
PART 01
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
如图,这些多边形有什么共同的特点?
等边三角形
正方形
正五边形
正六边形
点击打开
新课导入
各边相等,各内角也相等的多边形叫作正多边形.
正多边形定义
如果一个正多边形有 n 条边,那么这个正多边形
叫做正 n 边形.
思考: 菱形是正多边形吗?矩形是正多边形吗?
新课导入
新课讲解
第二部分
PART 02
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
如何作一个正多边形呢?
新课讲解
如何作一个正多边形呢?
将一个圆 n(n ≥ 3)等分, 依次连接各等分点所得的多边形叫作这个圆的内接正多边形, 这个圆是这个正多边形的外接圆, 正多边形的外接圆的圆心叫作正多边形的中心.
新课讲解
已知 ⊙O 的半径为 r, 求作 ⊙O 的内接正六边形.
因为正六边形每条边所对的圆心角为 60°,所以正六边形的边长与圆的半径相等. 因此在半径为 r 的圆上依次截取等于 r 的弦, 就可以将圆六等分.
新课讲解
已知 ⊙O 的半径为 r, 求作 ⊙O 的内接正六边形.
作法:(1)作⊙O 的任意直径 BE,分别以 B,E 为圆心,以 r 为半径作弧,与⊙O分别相交于点 A,C 和 F,D.
(2) 依次连接 AB,BC,CD,DE,EF, FA,则六边形 ABCDEF 就是所求作的⊙O 的内接正六边形.
新课讲解
如图,已知⊙O 的半径为 r,求作⊙O 的内接正方形.
分析 作两条互相垂直的直径,就可以将 ⊙O 四等分.
作法:(1)作直径 AC与 BD,使 AC ⊥ BD.
(2) 依次连接 AB,BC,CD,DA,则四边形 ABCD 就是所求作的 ⊙O 的内接正方形.
【教材P84页】
新课讲解
在生产设计中,人们经常会遇到等分圆的问题. 例如设计剪纸、齿轮、汽车轮毂等就是通过等分圆而得到的.
新课讲解
观察图中的正多边形,哪些是轴对称图形?哪些是中心对称图形?如果是轴对称图形,画出其对称轴; 如果是中心对称图形,找出其对称中心.
新课讲解
正多边形都是 图形,一个正 n 边形共有 条对称轴,每条对称轴都通过 n 边形的 .
轴对称
n
中心
边数是偶数的正多边形还是 ,它的中心就是对称中心.
中心对称图形
新课讲解
已知⊙O 的半径为 2 cm, 求作⊙O 的内接正方形和内接正六边形.
【教材P85页】
新课讲解
2. 许多图案设计都和圆有关,观察下图,请利用等分圆
的方法设计一幅图案.
【教材P86页】
新课讲解
课堂练习
第三部分
PART 03
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
1. 对于一个正多边形,下列四个命题中, 错误的是( )
A. 正多边形是轴对称图形, 每条边的垂直平分线是它的对称轴
B. 正多边形是中心对称图形, 正多边形的中心是它的对称中心
C. 正多边形每一个外角都等于正多边形的中心角
D. 正多边形每一个内角都与正多边形的中心角互补
B
课堂练习
2. 如图, 平面上两个正方形与正五边形都有一条公共边,
则∠α 等于( )
A. 45° B. 56°
C. 60° D. 72°
D
课堂练习
3. (贵阳中考)如图, 正六边形 ABCDEF 内接于☉O,
☉O 的半径为 6, OM ⊥ BC 于点 M , 则 OM 的长为
_______.
课堂练习
课堂小结
第四部分
PART 04
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
1.什么是正多边形?
2.如何画正多边形?
课堂小结
