北师版小学数学六年级上册第一单元 圆综合素养测评A卷(含答案)
文档属性
| 名称 | 北师版小学数学六年级上册第一单元 圆综合素养测评A卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 859.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-14 00:00:00 | ||
图片预览


文档简介
第一单元综合素养测评A卷
时间:60分钟 总分:100+10
一、填空题。(每空1分,共17分)
1. 战国时期墨家所著的《墨经》一书中记载:“圆,一中同长也。”它表示圆上任意一点到( )的距离都相等,也就是圆的( )都相等。
2. 如图,梯形的上底是( )cm,梯形的高是( )cm。
3. 用圆规在一个长10厘米,宽8厘米的长方形纸上画圆,这个圆的直径最大是( )厘米,圆规两脚间的距离最大是( )厘米。
4. 金箍棒全称如意金箍棒,是中国明代神魔小说《西游记》中孙悟空的标志性兵器。当金箍棒长8 dm时,如果抓住它的中点使其旋转,那么此时金箍棒旋转所形成的圆的面积是( )dm2。
5. 如果一个大圆的半径等于一个小圆的直径,那么大圆的周长是小圆周长的( )倍,小圆的面积是大圆面积的( )。
6. 一个半径是2厘米的圆形纸片,沿一条直径剪开,得到两个相同的半圆形纸片。每个半圆形纸片的面积是( )平方厘米,周长是( )厘米。
7. 一个杂技独轮车的车轮直径是40 cm,这个车轮向前滚动10周,前进了( )m。
8. 如图,小圆的周长是31.4 cm,它的半径是( )cm,圆环的面积是( )cm2。
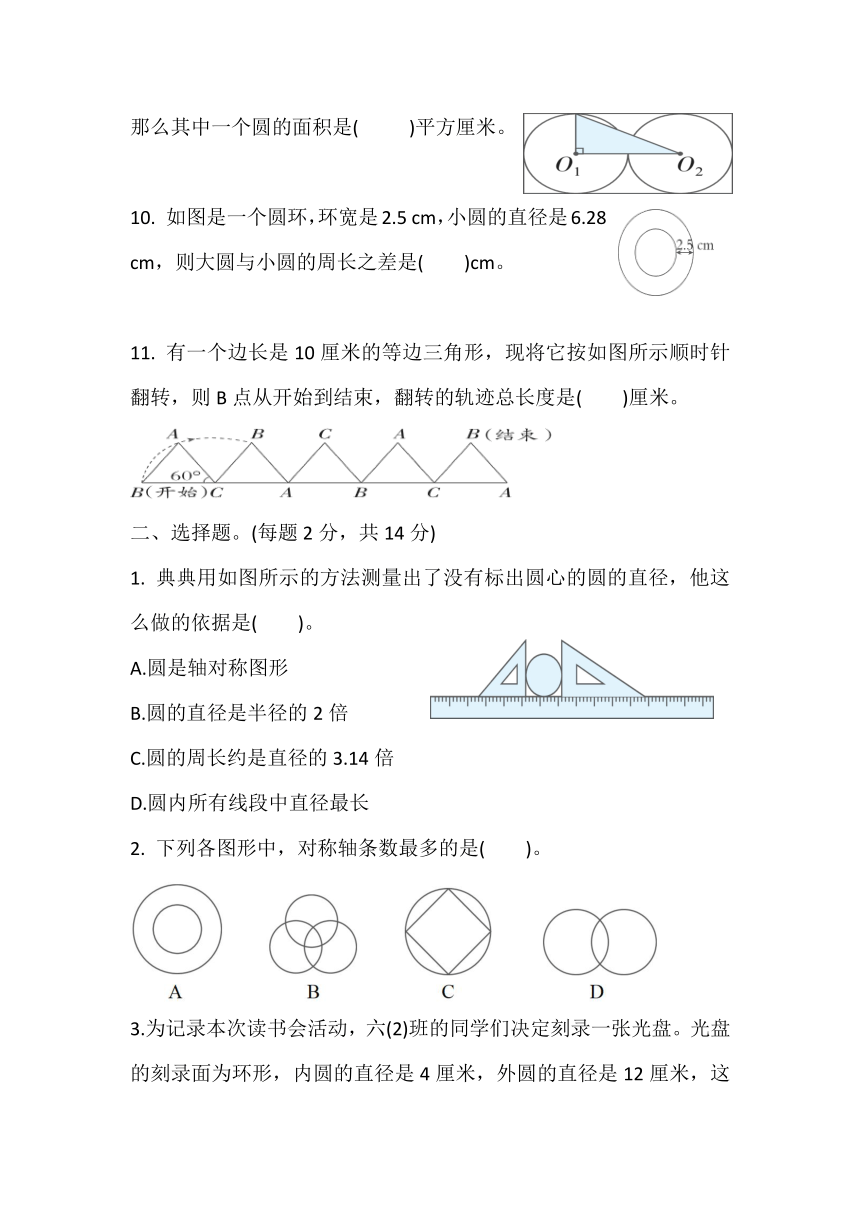
9. 如图,长方形里有两个等圆,如果涂色部分的面积是20平方厘米,那么其中一个圆的面积是( )平方厘米。
10. 如图是一个圆环,环宽是2.5 cm,小圆的直径是6.28 cm,则大圆与小圆的周长之差是( )cm。
11. 有一个边长是10厘米的等边三角形,现将它按如图所示顺时针翻转,则B点从开始到结束,翻转的轨迹总长度是( )厘米。
二、选择题。(每题2分,共14分)
1. 典典用如图所示的方法测量出了没有标出圆心的圆的直径,他这么做的依据是( )。
A.圆是轴对称图形
B.圆的直径是半径的2倍
C.圆的周长约是直径的3.14倍
D.圆内所有线段中直径最长
2. 下列各图形中,对称轴条数最多的是( )。
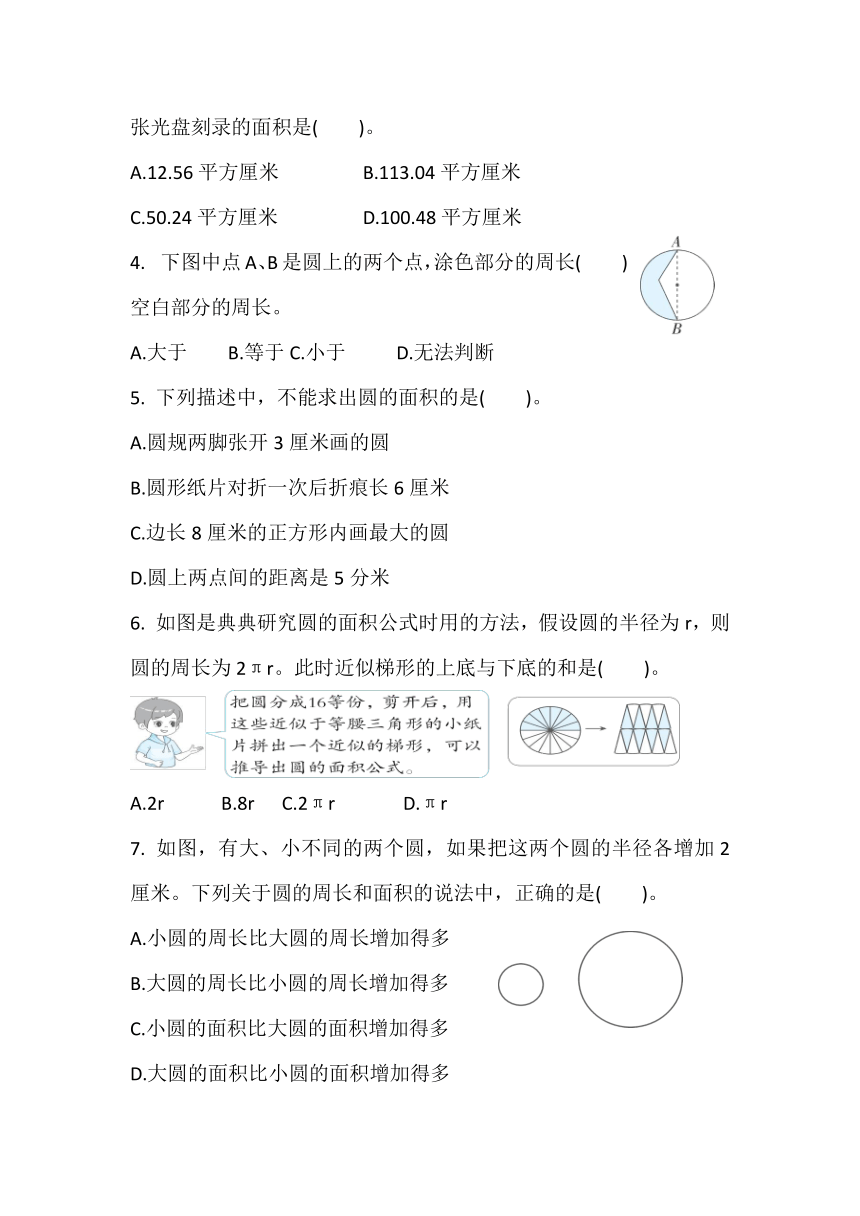
3.为记录本次读书会活动,六(2)班的同学们决定刻录一张光盘。光盘的刻录面为环形,内圆的直径是4厘米,外圆的直径是12厘米,这张光盘刻录的面积是( )。
A.12.56平方厘米 B.113.04平方厘米
C.50.24平方厘米 D.100.48平方厘米
4. 下图中点A、B是圆上的两个点,涂色部分的周长( )空白部分的周长。
A.大于 B.等于C.小于 D.无法判断
5. 下列描述中,不能求出圆的面积的是( )。
A.圆规两脚张开3厘米画的圆
B.圆形纸片对折一次后折痕长6厘米
C.边长8厘米的正方形内画最大的圆
D.圆上两点间的距离是5分米
6. 如图是典典研究圆的面积公式时用的方法,假设圆的半径为r,则圆的周长为2πr。此时近似梯形的上底与下底的和是( )。
A.2r B.8r C.2πr D.πr
7. 如图,有大、小不同的两个圆,如果把这两个圆的半径各增加2厘米。下列关于圆的周长和面积的说法中,正确的是( )。
A.小圆的周长比大圆的周长增加得多
B.大圆的周长比小圆的周长增加得多
C.小圆的面积比大圆的面积增加得多
D.大圆的面积比小圆的面积增加得多
三、计算题。(共25分)
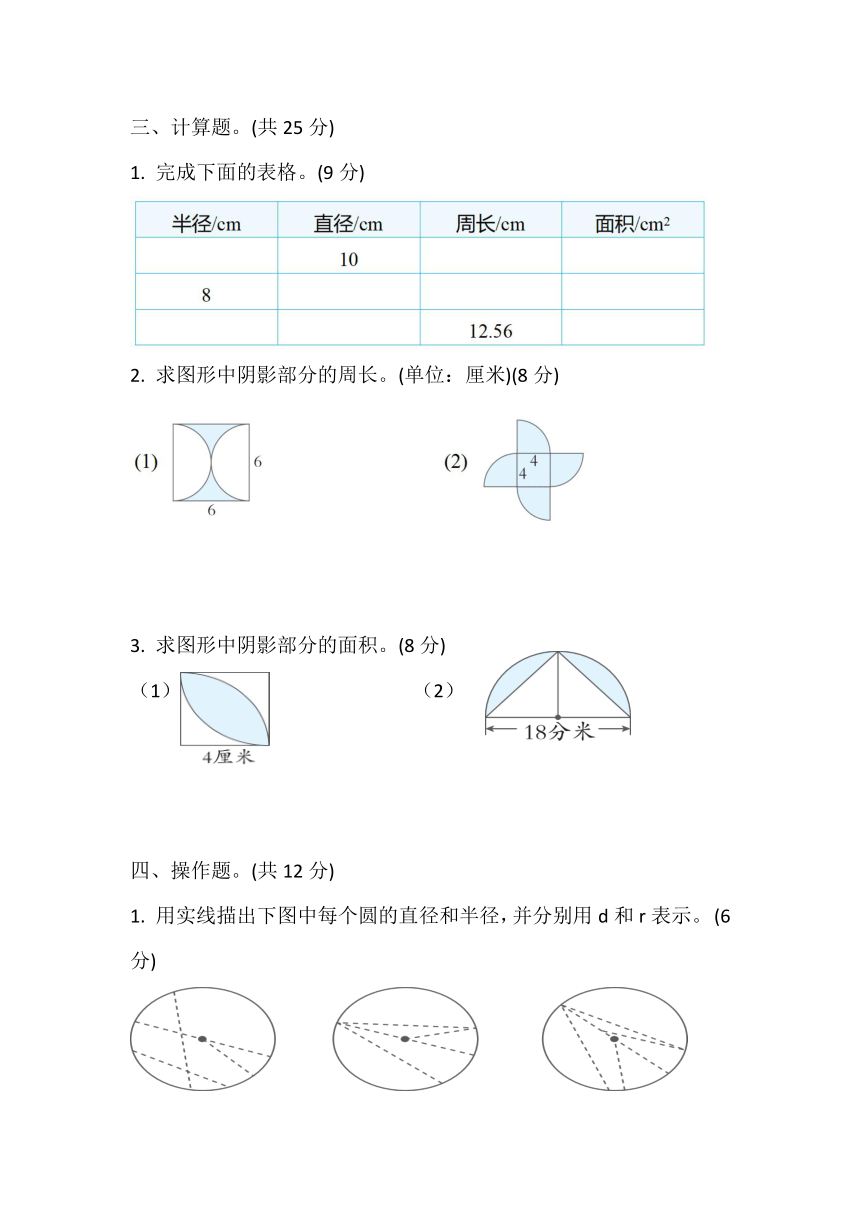
1. 完成下面的表格。(9分)
2. 求图形中阴影部分的周长。(单位:厘米)(8分)
3. 求图形中阴影部分的面积。(8分)
(1) (2)
四、操作题。(共12分)
1. 用实线描出下图中每个圆的直径和半径,并分别用d和r表示。 (6分)
2. 在下面的长方形中画出一个最大的半圆形,并求出半圆形的周长。(6分)
五、解决问题。(共32分)
1. 华华买了一个储蓄罐(如图),这个储蓄罐能放进一元的硬币吗?(5分)
2. 如图是龙龙家的扫地机器人,它的底面是一个圆形,直径是40 cm,将这个扫地机器人平放在地面上,它的占地面积是多少平方厘米?(5分)
3. 启德小学有一个半径是6米的圆形花坛,现准备在花坛周围铺一条9分米宽的鹅卵石小路,这条鹅卵石小路的占地面积是多少平方米?(5分)
4. 哥哥用一根铁丝围成一个半径是6 cm的圆(铁丝用完),弟弟用同样长的铁丝围成一个最大的正方形,这个正方形的边长是多少厘米?(5分)
5. 梦梦和天天从圆形场地的同一地点出发,沿着场地的边相背而行(如图),2分钟后两人相遇,梦梦每分钟走75 m,天天每分钟走82 m。这个圆形场地的占地面积是多少平方米?(6分)
6. 2024年巴黎奥运会于7月26日开幕,会上升起了奥运五环旗。奥运五环是由5个相同大小的圆环套接组成。如图,每个圆环的内外直径分别是10厘米和12厘米,每个圆环相交处的面积大约是4平方厘米。这个奥运五环的面积是多少平方厘米?(6分)
挑战题:天才的你,试一试。(共10分)
转化思想作为重要的数学思想方法之一,在我们的学习中无处不在。下面是一种有意思的推导圆的面积的方法。请先仔细观察下图,再填一填。
1. 上面转化过程中,圆的面积相当于( )。(4分)
2. 三角形的面积S=ah÷2,如果圆的半径是r,那么圆的面积
S=( )×( )÷2=( )。(用字母表示)(6分)
参考答案
一、1.圆心 半径
2.8 4
3.8 4
4.50.24
5.2
6.6.28 10.28
7.12.56
8.5 75.36
9.62.8
10.15.7
11.62.8
二、1.D 2.A 3.D 4.B 5.D 6.D 7.D
三、1.
(1)3.14×6+6×2=30.84(厘米)
(2)2×3.14×4+4×4=41.12(厘米)
(1)3.14×42÷2-4×4=9.12(平方厘米)
(2)18÷2=9(分米)
3.14×92÷2-18×9÷2=46.17(平方分米)
四、1.
2.
2×3.14×4÷2+4×2=20.56(厘米)
五、1.7.85÷3.14=2.5(cm) 2.5<2.55
答:这个储蓄罐能放进一元的硬币。
2.40÷2=20(cm) 3.14×202=1256(cm2)
答:它的占地面积是1256 cm2。
3.9分米=0.9米 3.14×[(6+0.9)2-62]=36.4554(平方米)
答:这条鹅卵石小路的占地面积是36.4554平方米。
4.2×3.14×6÷4=9.42(cm)
答:这个正方形的边长是9.42 cm。
5.(82+75)×2=314(m)
3.14×(314÷3.14÷2)2=7850(m2)
答:这个圆形场地的占地面积是7850 m2。
6.
挑战题:1.三角形的面积
解析:根据圆的面积公式的推导方法,通过观察题图可知,把这个用草绳编织成的圆形茶杯垫,沿一条半径将绳子剪断,并拉直,拼成了一个近似的三角形,这个三角形的底等于圆的周长,高等于圆的半径,虽然形状变了但是面积不变,所以圆的面积等于三角形的面积。
2.
解析:根据三角形的面积S=ah÷2,可以推导出圆的面积。
时间:60分钟 总分:100+10
一、填空题。(每空1分,共17分)
1. 战国时期墨家所著的《墨经》一书中记载:“圆,一中同长也。”它表示圆上任意一点到( )的距离都相等,也就是圆的( )都相等。
2. 如图,梯形的上底是( )cm,梯形的高是( )cm。
3. 用圆规在一个长10厘米,宽8厘米的长方形纸上画圆,这个圆的直径最大是( )厘米,圆规两脚间的距离最大是( )厘米。
4. 金箍棒全称如意金箍棒,是中国明代神魔小说《西游记》中孙悟空的标志性兵器。当金箍棒长8 dm时,如果抓住它的中点使其旋转,那么此时金箍棒旋转所形成的圆的面积是( )dm2。
5. 如果一个大圆的半径等于一个小圆的直径,那么大圆的周长是小圆周长的( )倍,小圆的面积是大圆面积的( )。
6. 一个半径是2厘米的圆形纸片,沿一条直径剪开,得到两个相同的半圆形纸片。每个半圆形纸片的面积是( )平方厘米,周长是( )厘米。
7. 一个杂技独轮车的车轮直径是40 cm,这个车轮向前滚动10周,前进了( )m。
8. 如图,小圆的周长是31.4 cm,它的半径是( )cm,圆环的面积是( )cm2。
9. 如图,长方形里有两个等圆,如果涂色部分的面积是20平方厘米,那么其中一个圆的面积是( )平方厘米。
10. 如图是一个圆环,环宽是2.5 cm,小圆的直径是6.28 cm,则大圆与小圆的周长之差是( )cm。
11. 有一个边长是10厘米的等边三角形,现将它按如图所示顺时针翻转,则B点从开始到结束,翻转的轨迹总长度是( )厘米。
二、选择题。(每题2分,共14分)
1. 典典用如图所示的方法测量出了没有标出圆心的圆的直径,他这么做的依据是( )。
A.圆是轴对称图形
B.圆的直径是半径的2倍
C.圆的周长约是直径的3.14倍
D.圆内所有线段中直径最长
2. 下列各图形中,对称轴条数最多的是( )。
3.为记录本次读书会活动,六(2)班的同学们决定刻录一张光盘。光盘的刻录面为环形,内圆的直径是4厘米,外圆的直径是12厘米,这张光盘刻录的面积是( )。
A.12.56平方厘米 B.113.04平方厘米
C.50.24平方厘米 D.100.48平方厘米
4. 下图中点A、B是圆上的两个点,涂色部分的周长( )空白部分的周长。
A.大于 B.等于C.小于 D.无法判断
5. 下列描述中,不能求出圆的面积的是( )。
A.圆规两脚张开3厘米画的圆
B.圆形纸片对折一次后折痕长6厘米
C.边长8厘米的正方形内画最大的圆
D.圆上两点间的距离是5分米
6. 如图是典典研究圆的面积公式时用的方法,假设圆的半径为r,则圆的周长为2πr。此时近似梯形的上底与下底的和是( )。
A.2r B.8r C.2πr D.πr
7. 如图,有大、小不同的两个圆,如果把这两个圆的半径各增加2厘米。下列关于圆的周长和面积的说法中,正确的是( )。
A.小圆的周长比大圆的周长增加得多
B.大圆的周长比小圆的周长增加得多
C.小圆的面积比大圆的面积增加得多
D.大圆的面积比小圆的面积增加得多
三、计算题。(共25分)
1. 完成下面的表格。(9分)
2. 求图形中阴影部分的周长。(单位:厘米)(8分)
3. 求图形中阴影部分的面积。(8分)
(1) (2)
四、操作题。(共12分)
1. 用实线描出下图中每个圆的直径和半径,并分别用d和r表示。 (6分)
2. 在下面的长方形中画出一个最大的半圆形,并求出半圆形的周长。(6分)
五、解决问题。(共32分)
1. 华华买了一个储蓄罐(如图),这个储蓄罐能放进一元的硬币吗?(5分)
2. 如图是龙龙家的扫地机器人,它的底面是一个圆形,直径是40 cm,将这个扫地机器人平放在地面上,它的占地面积是多少平方厘米?(5分)
3. 启德小学有一个半径是6米的圆形花坛,现准备在花坛周围铺一条9分米宽的鹅卵石小路,这条鹅卵石小路的占地面积是多少平方米?(5分)
4. 哥哥用一根铁丝围成一个半径是6 cm的圆(铁丝用完),弟弟用同样长的铁丝围成一个最大的正方形,这个正方形的边长是多少厘米?(5分)
5. 梦梦和天天从圆形场地的同一地点出发,沿着场地的边相背而行(如图),2分钟后两人相遇,梦梦每分钟走75 m,天天每分钟走82 m。这个圆形场地的占地面积是多少平方米?(6分)
6. 2024年巴黎奥运会于7月26日开幕,会上升起了奥运五环旗。奥运五环是由5个相同大小的圆环套接组成。如图,每个圆环的内外直径分别是10厘米和12厘米,每个圆环相交处的面积大约是4平方厘米。这个奥运五环的面积是多少平方厘米?(6分)
挑战题:天才的你,试一试。(共10分)
转化思想作为重要的数学思想方法之一,在我们的学习中无处不在。下面是一种有意思的推导圆的面积的方法。请先仔细观察下图,再填一填。
1. 上面转化过程中,圆的面积相当于( )。(4分)
2. 三角形的面积S=ah÷2,如果圆的半径是r,那么圆的面积
S=( )×( )÷2=( )。(用字母表示)(6分)
参考答案
一、1.圆心 半径
2.8 4
3.8 4
4.50.24
5.2
6.6.28 10.28
7.12.56
8.5 75.36
9.62.8
10.15.7
11.62.8
二、1.D 2.A 3.D 4.B 5.D 6.D 7.D
三、1.
(1)3.14×6+6×2=30.84(厘米)
(2)2×3.14×4+4×4=41.12(厘米)
(1)3.14×42÷2-4×4=9.12(平方厘米)
(2)18÷2=9(分米)
3.14×92÷2-18×9÷2=46.17(平方分米)
四、1.
2.
2×3.14×4÷2+4×2=20.56(厘米)
五、1.7.85÷3.14=2.5(cm) 2.5<2.55
答:这个储蓄罐能放进一元的硬币。
2.40÷2=20(cm) 3.14×202=1256(cm2)
答:它的占地面积是1256 cm2。
3.9分米=0.9米 3.14×[(6+0.9)2-62]=36.4554(平方米)
答:这条鹅卵石小路的占地面积是36.4554平方米。
4.2×3.14×6÷4=9.42(cm)
答:这个正方形的边长是9.42 cm。
5.(82+75)×2=314(m)
3.14×(314÷3.14÷2)2=7850(m2)
答:这个圆形场地的占地面积是7850 m2。
6.
挑战题:1.三角形的面积
解析:根据圆的面积公式的推导方法,通过观察题图可知,把这个用草绳编织成的圆形茶杯垫,沿一条半径将绳子剪断,并拉直,拼成了一个近似的三角形,这个三角形的底等于圆的周长,高等于圆的半径,虽然形状变了但是面积不变,所以圆的面积等于三角形的面积。
2.
解析:根据三角形的面积S=ah÷2,可以推导出圆的面积。
同课章节目录
- 一 圆
- 1 圆的认识(一)
- 2 圆的认识(二)
- 3 欣赏与设计
- 4 圆的周长
- 5 圆的面积(一)
- 6 圆的面积(二)
- 二 分数的混合运算
- 1 分数的混合运算(一)
- 2 分数的混合运算(二)
- 3 分数的混合运算(三)
- 三 观察物体
- 1 搭积木比赛
- 2 观察的范围
- 3 天安门广场
- 四 百分数
- 1 百分数的认识
- 2 合格率
- 3 营养含量
- 4 这月我当家
- 五 数据处理
- 1 扇形统计图
- 2 统计图的选择
- 3 身高的情况
- 4 身高的变化
- 六 比的认识
- 1 生活中的比
- 2 比的化简
- 3 比的应用
- 数学好玩
- 1 反弹高度
- 2 看图找关系
- 3 比赛场次
- 七 百分数的应用
- 1 百分数的应用(一)
- 2 百分数的应用(二)
- 3 百分数的应用(三)
- 4 百分数的应用(四)
