2025年浙江省中考数学一轮复习专题检测 专题26 图形的轴对称、平移与旋转(含解析)
文档属性
| 名称 | 2025年浙江省中考数学一轮复习专题检测 专题26 图形的轴对称、平移与旋转(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-14 21:28:28 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
专题26 图形的轴对称、平移与旋转
一.选择题
1.(2024 滨州)数学中有许多精美的曲线,以下是“悬链线”“黄金螺旋线”“三叶玫瑰线”和“笛卡尔心形线”.其中不是轴对称图形的是( )
A. B. C. D.
2.(2024 大庆)垃圾分类功在当代,利在千秋.下列垃圾分类指引标志中,文字上方的图形既是轴对称图形又是中心对称图形的是( )
A.厨余垃圾 B.有害垃圾 C.其他垃圾 D.可回收物
3.(2024 拱墅区一模)在平面直角坐标系中,点A(2,﹣3)与点B(a,b)关于y轴对称,则( )
A.a=2,b=﹣3 B.a=2,b=3 C.a=﹣2,b=﹣3 D.a=﹣2,b=3
4.(2024 海南)平面直角坐标系中,将点A向右平移3个单位长度得到点A′(2,1),则点A的坐标是( )
A.(5,1) B.(2,4) C.(﹣1,1) D.(2,﹣2)
5.(2024 天津)如图,△ABC中,∠B=30°,将△ABC绕点C顺时针旋转60°得到△DEC,点A,B的对应点分别为D,E,延长BA交DE于点F,下列结论一定正确的是( )
A.∠ACB=∠ACD B.AC∥DE C.AB=EF D.BF⊥CE
6.(2025 沁阳市二模)如图,点A(0,﹣2),B(1,0),将线段AB平移得到线段DC,若∠ABC=90°,BC=2AB,则点D的坐标是( )
A.(4,﹣4) B.(4,﹣6) C.(6,﹣2) D.(3,﹣4)
7.(2024 鹿城区校级模拟)如图,把一张长方形纸片ABCD沿PQ,MN折叠.顶点A、B,C,D的对应点分别为A′,B′,C′,D′,点B′与D′重合,点A′恰与BC,MD′的交点重合.若CD=2,A′M=3,则AD的长为( )
A.12cm B. C. D.15cm
8.(2025 浙江模拟)如图,E,F分别是正方形ABCD的边AD,BC上的点,将正方形纸片ABCD沿EF折叠,使得点B的对应点B'恰好落在边CD上,要想知道正方形ABCD的边长,只需知道( )
A.BF的长度 B.△B′CF的周长 C.△B′DG的周长 D.△A′EG的面积
9.(2024 椒江区二模)如图,将三角形ABC(AC>AB)沿BC方向平移得到△DEF,使,DE与AC交于点M,以下关于四边形DMCF和四边形ABEM周长的说法,正确的是( )
A.周长之差可由(AC﹣AB)值确定
B.周长之和可由(AC+AB)值确定
C.周长之差可由(AC﹣AB+BC)值确定
D.周长之和可由(AC+AB+BC)值确定
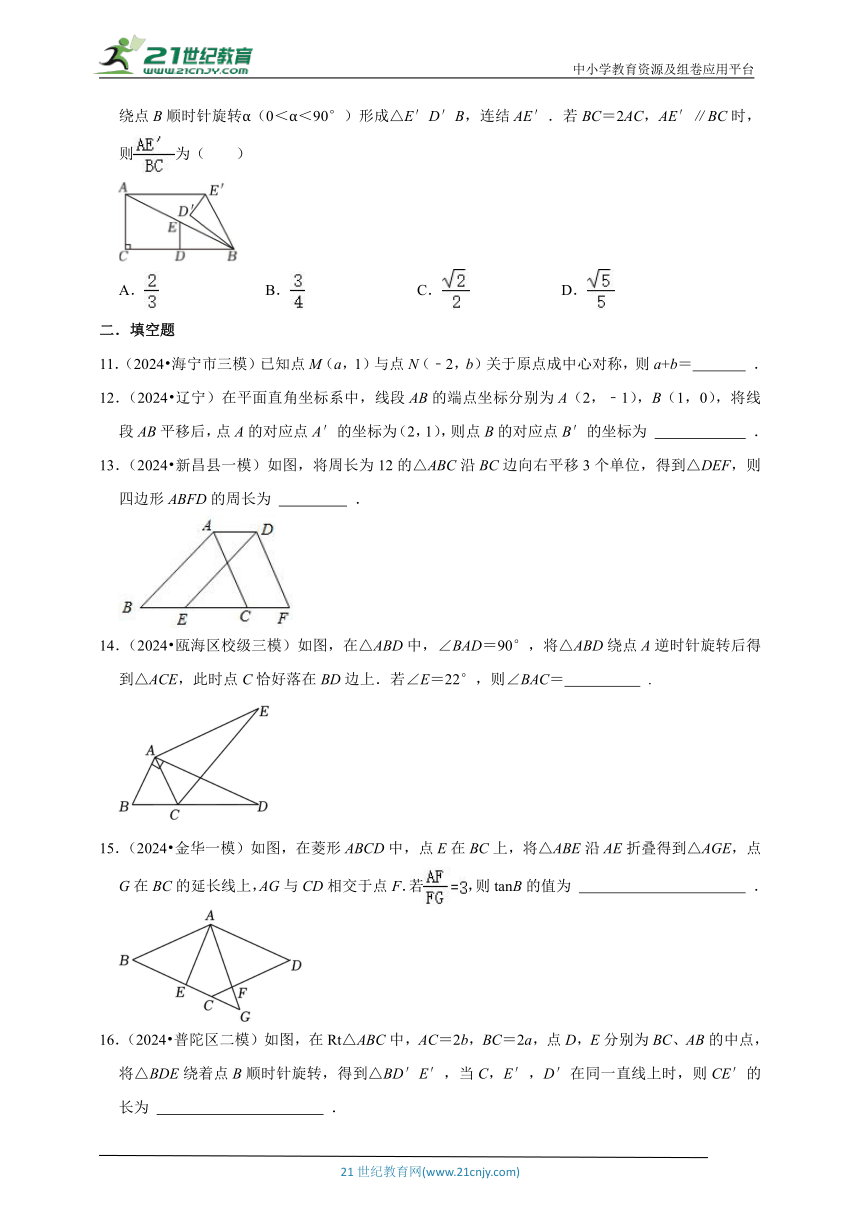
10.(2024 舟山一模)如图,在Rt△ABC中,∠ACB=90°,D,E分别为BC,AB的中点,将△EDB绕点B顺时针旋转α(0<α<90°)形成△E′D′B,连结AE′.若BC=2AC,AE′∥BC时,则为( )
A. B. C. D.
二.填空题
11.(2024 海宁市三模)已知点M(a,1)与点N(﹣2,b)关于原点成中心对称,则a+b= .
12.(2024 辽宁)在平面直角坐标系中,线段AB的端点坐标分别为A(2,﹣1),B(1,0),将线段AB平移后,点A的对应点A′的坐标为(2,1),则点B的对应点B′的坐标为 .
13.(2024 新昌县一模)如图,将周长为12的△ABC沿BC边向右平移3个单位,得到△DEF,则四边形ABFD的周长为 .
14.(2024 瓯海区校级三模)如图,在△ABD中,∠BAD=90°,将△ABD绕点A逆时针旋转后得到△ACE,此时点C恰好落在BD边上.若∠E=22°,则∠BAC= .
15.(2024 金华一模)如图,在菱形ABCD中,点E在BC上,将△ABE沿AE折叠得到△AGE,点G在BC的延长线上,AG与CD相交于点F.若,则tanB的值为 .
16.(2024 普陀区二模)如图,在Rt△ABC中,AC=2b,BC=2a,点D,E分别为BC、AB的中点,将△BDE绕着点B顺时针旋转,得到△BD′E′,当C,E′,D′在同一直线上时,则CE′的长为 .
三.解答题
17.(2024 金华一模)如图,在边长为1的小正方形组成的网格中建立直角坐标系,小正方形的顶点为格点,△ABC与△EFG的顶点都在格点上.
(1)作△A1B1C1,使△A1B1C1与△ABC关于原点O成中心对称.
(2)已知△ABC与△EFG关于点P成中心对称,请在图中画出点P的位置,并写出该点的坐标.
18.(2024 温岭市一模)如图,在矩形ABCD中,点E是边BC上一点,连结AE,将△ABE沿着AE折叠得到△AFE,延长EF恰好经过点D.
(1)求证:△ADF≌△DEC.
(2)若AB=6,AD=10,求△EDC的周长.
19.(2025 衢州一模)如图,在△ABC中,CA=CB,D是△ABC内一点,连结CD,将线段CD绕点C逆时针旋转到CE,使∠DCE=∠ACB,连结AD,DE,BE.
(1)求证:△CAD≌△CBE.
(2)当∠CAB=60°时,求∠CBE与∠BAD的度数和.
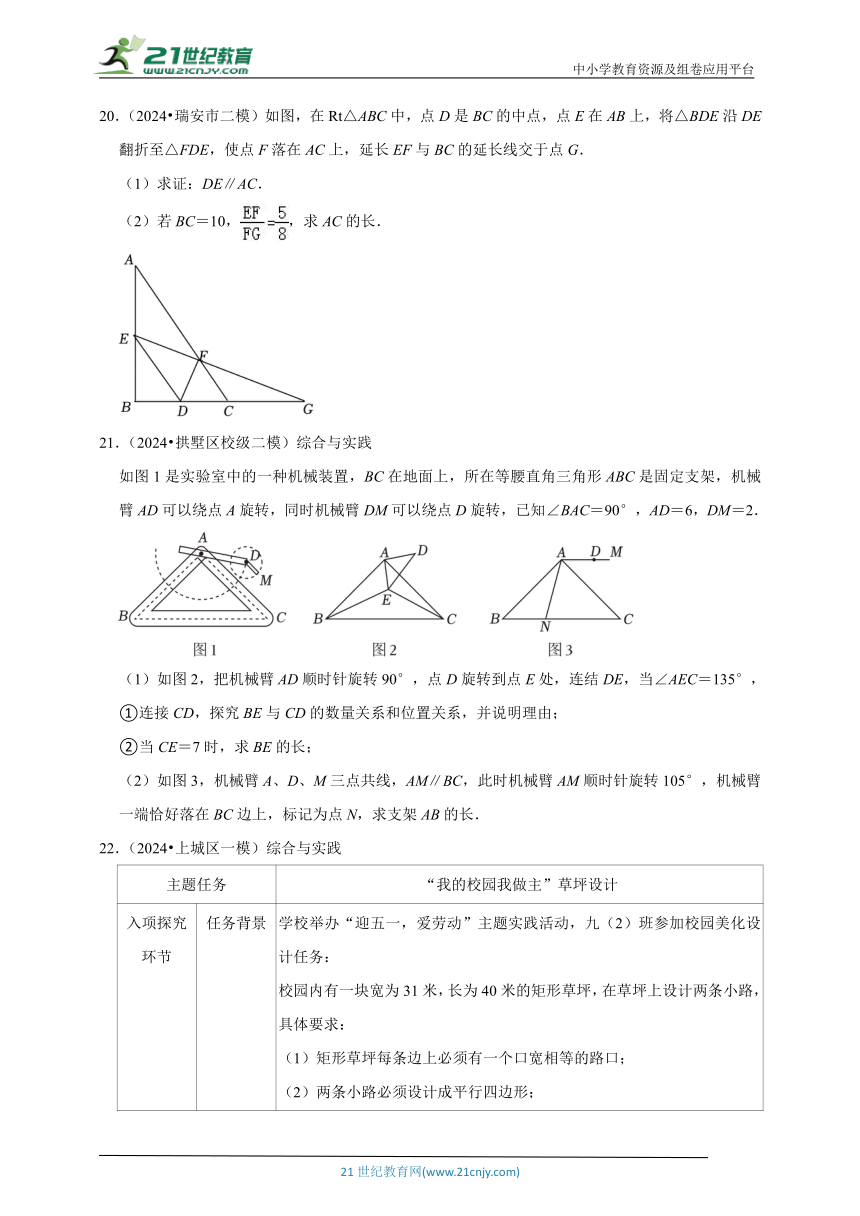
20.(2024 瑞安市二模)如图,在Rt△ABC中,点D是BC的中点,点E在AB上,将△BDE沿DE翻折至△FDE,使点F落在AC上,延长EF与BC的延长线交于点G.
(1)求证:DE∥AC.
(2)若BC=10,,求AC的长.
21.(2024 拱墅区校级二模)综合与实践
如图1是实验室中的一种机械装置,BC在地面上,所在等腰直角三角形ABC是固定支架,机械臂AD可以绕点A旋转,同时机械臂DM可以绕点D旋转,已知∠BAC=90°,AD=6,DM=2.
(1)如图2,把机械臂AD顺时针旋转90°,点D旋转到点E处,连结DE,当∠AEC=135°,
①连接CD,探究BE与CD的数量关系和位置关系,并说明理由;
②当CE=7时,求BE的长;
(2)如图3,机械臂A、D、M三点共线,AM∥BC,此时机械臂AM顺时针旋转105°,机械臂一端恰好落在BC边上,标记为点N,求支架AB的长.
22.(2024 上城区一模)综合与实践
主题任务 “我的校园我做主”草坪设计
入项探究环节 任务背景 学校举办“迎五一,爱劳动”主题实践活动,九(2)班参加校园美化设计任务: 校园内有一块宽为31米,长为40米的矩形草坪,在草坪上设计两条小路, 具体要求: (1)矩形草坪每条边上必须有一个口宽相等的路口; (2)两条小路必须设计成平行四边形;
驱动任务一 九(2)班各个实践小组的设计方案汇总后,主要有甲、乙、丙三种不同的方案(如图1): (1)直观猜想:方案中小路的总面积大小关系:S甲 S乙,S甲 S丙;(请填“相等”或“不相等”)
深入探究 驱动任务二 验证猜想:各个实践小组用如表格进行研究: 方案纵向小路面积横向小路面积纵横交叉面积小路总面积乙方案31x40x甲方案31x40x丙方案31x40x
(2)请用含x的代数式表示甲方案中小路总面积: ;
驱动任务三 (3)如果甲种方案除小路后草坪总面积约为1170平方米.请计算两条小路的宽度是多少?
拓展探究 驱动任务四 为了深入研究,各个小组选择丙方案(如图2)进行研究.若两条小路与矩形两组对边所夹锐角∠BGF=∠AEF=θ. (4)若θ=60°时,用含x的代数式拓表示四边形FHPQ的边长FH; (5)若x=1时,请用含θ的三角函数表示两条路重叠部分四边形FHPQ的面积,并写出sinθ取值范围.
答案与解析
一.选择题
1.(2024 滨州)数学中有许多精美的曲线,以下是“悬链线”“黄金螺旋线”“三叶玫瑰线”和“笛卡尔心形线”.其中不是轴对称图形的是( )
A. B. C. D.
【点拨】根据轴对称图形的概念求解.
【解析】解:A、是轴对称图形;
B、不是轴对称图形;
C、是轴对称图形;
D、是轴对称图形;
故选:B.
【点睛】本题考查了轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.
2.(2024 大庆)垃圾分类功在当代,利在千秋.下列垃圾分类指引标志中,文字上方的图形既是轴对称图形又是中心对称图形的是( )
A.厨余垃圾 B.有害垃圾 C.其他垃圾 D.可回收物
【点拨】一个平面内,如果一个图形沿一条直线折叠,若折叠后直线两旁的部分能够完全重合,那么这个图形即为轴对称图形;一个平面内,如果一个图形绕某个点旋转180°,若旋转后的图形与原来的图形完全重合,那么这个图形即为中心对称图形;据此进行判断即可.
【解析】解:A是轴对称图形,但它不是中心对称图形,则A不符合题意;
B既是轴对称图形,也是中心对称图形,则B符合题意;
C不是轴对称图形,也不是中心对称图形,则C不符合题意;
D不是轴对称图形,也不是中心对称图形,则D不符合题意;
故选:B.
【点睛】本题考查轴对称图形及中心对称图形,熟练掌握其定义是解题的关键.
3.(2024 拱墅区一模)在平面直角坐标系中,点A(2,﹣3)与点B(a,b)关于y轴对称,则( )
A.a=2,b=﹣3 B.a=2,b=3 C.a=﹣2,b=﹣3 D.a=﹣2,b=3
【点拨】根据“关于y轴对称的点,纵坐标相同,横坐标互为相反数”即可求出a、b的值.
【解析】解:在平面直角坐标系中,点A(2,﹣3)与点B(a,b)关于y轴对称,则a=﹣2,b=﹣3.
故选:C.
【点睛】本题考查了关于y轴对称的点的坐标,解决本题的关键是掌握好对称点的坐标规律:关于y轴对称的点,纵坐标相同,横坐标互为相反数.
4.(2024 海南)平面直角坐标系中,将点A向右平移3个单位长度得到点A′(2,1),则点A的坐标是( )
A.(5,1) B.(2,4) C.(﹣1,1) D.(2,﹣2)
【点拨】将点A'的横坐标减3,纵坐标不变即可得到点A的坐标.
【解析】解:将点A向右平移3个单位长度后得到点A'(2,1),
∴点A的坐标是(2﹣3,1),即点A的坐标为(﹣1,1),
故选:C.
【点睛】此题主要考查了坐标与图形变化﹣平移,关键是掌握平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.
5.(2024 天津)如图,△ABC中,∠B=30°,将△ABC绕点C顺时针旋转60°得到△DEC,点A,B的对应点分别为D,E,延长BA交DE于点F,下列结论一定正确的是( )
A.∠ACB=∠ACD B.AC∥DE C.AB=EF D.BF⊥CE
【点拨】先根据旋转性质得∠BCE=∠ACD=60°,结合∠B=30°,即可得证BF⊥CE,再根据同旁内角互补证明两直线平行,来分析AC∥DE不一定成立;根据图形性质以及角的运算或线段的运算得出A和C选项是错误的.
【解析】解:设BF与CE相交于点H,如图所示:
∵△ABC中,将△ABC绕点C顺时针旋转60°得到△DEC,
∴∠BCE=∠ACD=60°,
∵∠B=30°,
∴在△BHC中,∠BHC=180°﹣∠BCE﹣∠B=90°,
∴BF⊥CE,故D选项正确;
设∠ACH=x°,
∴∠ACB=60°﹣x°,
∵∠B=30°,
∴∠EDC=∠BAC=180°﹣30°﹣(60°﹣x°)=90°+x°,
∴∠EDC+∠ACD=90°+x°+60°=150°+x°,
∵x°不一定等于30°,
∴∠EDC+∠ACD不一定等于180°,
∴AC∥DE不一定成立,故B选项不正确;
∵∠ACB=60°﹣x°,∠ACD=60°,x°不一定等于0°,
∴∠ACB=∠ACD不一定成立,故A选项不正确;
∵将△ABC绕点C顺时针旋转60°得到△DEC,
∴AB=ED=EF+FD,
∴BA>EF,故C选项不正确;
故选:D.
【点睛】本题考查了旋转性质以及两个锐角互余的三角形是直角三角形,平行线的判定,正确掌握相关性质内容是解题的关键.
6.(2025 沁阳市二模)如图,点A(0,﹣2),B(1,0),将线段AB平移得到线段DC,若∠ABC=90°,BC=2AB,则点D的坐标是( )
A.(4,﹣4) B.(4,﹣6) C.(6,﹣2) D.(3,﹣4)
【点拨】过点D作DE⊥y轴于点E,利用点A,B的坐标表示出线段OA,OB的长,利用平移的性质和矩形的判定定理得到四边形ABCD是矩形;利用相似三角形的判定与性质求得线段DE,AE的长,进而得到OE的长,则结论可得.
【解析】解:过点D作DE⊥y轴于点E,如图,
∵点A(0,﹣2)、B(1,0),
∴OA=2,OB=1.
∵线段AB平移得到线段DC,
∴AB∥CD,AB=CD,
∴四边形ABCD是平行四边形,
∵∠ABC=90°,
∴四边形ABCD是矩形,
∴∠BAD=90°,BC=AD,
∵BC=2AB,
∴AD=2AB,
∵∠BAO+∠DAE=90°,∠BAO+∠ABO=90°,
∴∠ABO=∠EAD.
∵∠AOB=∠AED=90°,
∴△ABO∽△DAE.
∴===,
∴DE=2OA=4,AE=2OB=2,
∴OE=OA+AE=4,
∴D(4,﹣4).
故选:A.
【点睛】本题主要考查了坐标与图形变化﹣平移,矩形的判定与性质,相似三角形的判定与性质,利用点的坐标表示出相应线段的长度是解题的关键.
7.(2024 鹿城区校级模拟)如图,把一张长方形纸片ABCD沿PQ,MN折叠.顶点A、B,C,D的对应点分别为A′,B′,C′,D′,点B′与D′重合,点A′恰与BC,MD′的交点重合.若CD=2,A′M=3,则AD的长为( )
A.12cm B. C. D.15cm
【点拨】过点A'作A'E⊥C'N于点E,在Rt△A'NE中,求出A'N,A'E,NE,证明△A'QB'∽△NA'E,利用对应边成比例求出A'Q,B'Q,再利用线段间的关系即可求出BC,从而得到AD的长.
【解析】解:过点A'作A'E⊥C'N于点E,如图,
由题意,知四边形A'B'C'E是矩形,
∴A'E=D'C'=DC=2,EC'=A′B'=AB=DC=2,
∵把一张长方形纸片ABCD沿PQ,MN折叠.
∴AD∥BC,∠DMN=∠A'MN,
∴∠DMN=∠A'NM=∠A'MN,
∴A'N=A'M=3,
在Rt△A'NE中,
由勾股定理,得NE===,
由题意,知A'E∥QB',
∴∠A'QB'=∠NA'E,
又∵∠A'B'Q=∠NEA'=90°,
∴△A'QB'∽△NA'E,
∴====,
∴A'Q=NA'=×3=,
QB'=A'E=×2=,
∴BQ=QB'=,NC=NC'=NE+EC'=+2,
∴AD=BC=BQ+A'Q+A'N+NC=++3++2=,
故选:B.
【点睛】本题考查翻折变换,矩形的性质,勾股定理,相似三角形的判定和性质,弄清图形中相关线段之间的关系,掌握相关图形的性质和判定是解题的关键.
8.(2025 浙江模拟)如图,E,F分别是正方形ABCD的边AD,BC上的点,将正方形纸片ABCD沿EF折叠,使得点B的对应点B'恰好落在边CD上,要想知道正方形ABCD的边长,只需知道( )
A.BF的长度 B.△B′CF的周长 C.△B′DG的周长 D.△A′EG的面积
【点拨】证明△DB′G∽△CFB′,可得==,故DB'+DG+B'G==,即可证明DB'+DG+B'G=2AB,故要想知道正方形ABCD的边长,只需知道△B′DG的周长.
【解析】解:∵四边形ABCD是正方形,
∴∠D=∠C=∠B=90°,BC=CD=AB,
由折叠得∠GB′F=∠B=90°,B′F=BF,
∴DB′=CD﹣B′C=BC﹣B′C,CF+B′F=CF+BF=BC,BF2﹣B′C2=B′F2﹣B′C2=CF2,∠DB′G=∠CFB′=90°﹣∠CB′F,
∴△DB′G∽△CFB′,
∴==,
∴==,
∴DB'+DG+B'G==,
∵====2(BF+CF)=2AB,
∴DB'+DG+B'G=2AB,
∴要想知道正方形ABCD的边长,只需知道△B′DG的周长;
故选:C.
【点睛】本题考查折叠变化,涉及相似三角形的判定与性质,正方形性质及应用,解题的关键是需要有较强的运算,变形的能力.
9.(2024 椒江区二模)如图,将三角形ABC(AC>AB)沿BC方向平移得到△DEF,使,DE与AC交于点M,以下关于四边形DMCF和四边形ABEM周长的说法,正确的是( )
A.周长之差可由(AC﹣AB)值确定 B.周长之和可由(AC+AB)值确定
C.周长之差可由(AC﹣AB+BC)值确定 D.周长之和可由(AC+AB+BC)值确定
【点拨】根据平移的性质得出周长关系解答即可.
【解析】解:由平移可知,BE=CF,AB=DE,AC=DF,BC=EF,
∵BE=BC,
∴EC=2BE,BC=3BE,
∴四边形DMCF和四边形ABEM周长之差=(DM+MC+CF+DF)﹣(AB+BE+AM+ME)=(AB﹣ME+AC﹣AM+BE+AC)﹣(AB+BE+AM+ME)=AB﹣ME+AC﹣AM+BE+AC﹣AB﹣BE﹣AM﹣ME=2AC﹣2ME﹣2AM=,
四边形DMCF和四边形ABEM周长之和=(DM+MC+CF+DF)+(AB+BE+AM+ME)=(AB﹣ME+AC﹣AM+BE+AC)+(AB+BE+AM+ME)=2AB+2BE+2AC=2AB+BC+2AC,
∴周长之差可由(AC﹣AB)值确定,
故选:A.
【点睛】此题考查平移的性质,关键是根据平移的性质得出周长关系解答.
10.(2024 舟山一模)如图,在Rt△ABC中,∠ACB=90°,D,E分别为BC,AB的中点,将△EDB绕点B顺时针旋转α(0<α<90°)形成△E′D′B,连结AE′.若BC=2AC,AE′∥BC时,则为( )
A. B. C. D.
【点拨】根据BC=2AC,可设出BC及AC的长,过点B作AE′的垂线,垂足为M,利用勾股定理表示出E′M的长,进而可表示出AE′的长,据此可解决问题.
【解析】解:∵BC=2AC,
∴令AC=a,BC=2a.
在Rt△ABC中,
AB=.
又∵点D,E分别为BC和AB的中点,
∴BD=a,BE=.
由旋转可知,
D′E′=DE=a,BE′=BE=.
过点B作AE′的垂线,垂足为M,
∵AE′∥BC,
∴∠E′AC+∠C=180°,
又∵∠C=90°,
∴∠E′AC=90°,
∴四边形ACBM为矩形,
∴BM=AC=a,AM=BC=2a.
在Rt△BE′M中,
ME′=,
∴AE′=2a﹣,
∴.
故选:B.
【点睛】本题考查旋转的性质及三角形中位线定理,熟知图形旋转的性质是解题的关键.
二.填空题
11.(2024 海宁市三模)已知点M(a,1)与点N(﹣2,b)关于原点成中心对称,则a+b= 1 .
【点拨】关于原点成中心对称的点的横坐标互为相反数,纵坐标互为相反数,由此可得a,b的值,进而可得答案.
【解析】解:∵点M(a,1)与点N(﹣2,b)关于原点成中心对称,
∴a=2,b=﹣1,
∴a+b=2﹣1=1.
故答案为:1.
【点睛】本题考查关于原点对称的点的坐标,解题的关键是熟知关于原点成中心对称的点的横坐标互为相反数,纵坐标互为相反数.
12.(2024 辽宁)在平面直角坐标系中,线段AB的端点坐标分别为A(2,﹣1),B(1,0),将线段AB平移后,点A的对应点A′的坐标为(2,1),则点B的对应点B′的坐标为 (1,2) .
【点拨】根据点A及点A对应点的坐标,得出平移的方向和距离,据此可解决问题.
【解析】解:因为点A坐标为(2,﹣1),且平移后对应点A′的坐标为(2,1),
所以2﹣2=0,1﹣(﹣1)=2,
所以1+0=1,0+2=2,
所以点B的对应点B′的坐标为(1,2).
故答案为:(1,2).
【点睛】本题主要考查了坐标与图形变化﹣平移,熟知图形平移的性质是解题的关键.
13.(2024 新昌县一模)如图,将周长为12的△ABC沿BC边向右平移3个单位,得到△DEF,则四边形ABFD的周长为 18 .
【点拨】根据平移的性质,对应点的连线AD、CF都等于平移距离,再根据四边形ABFD的周长=△ABC的周长+AD+CF代入数据计算即可得解.
【解析】解:∵△ABC沿BC方向平移2个单位得到△DEF,
∴AD=CF=2,
∴四边形ABFD的周长
=AB+BC+DF+CF+AD
=△ABC的周长+AD+CF
=12+3+3
=18.
故答案为:18.
【点睛】本题考查了平移的性质,主要利用了对应点的连线等于平移距离,结合图形表示出四边形ABFD的周长是解题的关键.
14.(2024 瓯海区校级三模)如图,在△ABD中,∠BAD=90°,将△ABD绕点A逆时针旋转后得到△ACE,此时点C恰好落在BD边上.若∠E=22°,则∠BAC= 44° .
【点拨】由旋转得,AB=AC,∠D=∠E=22°,则∠B=∠ACB=180°﹣∠BAD﹣∠D=68°,再根据∠BAC=180°﹣∠B﹣∠ACB可得答案.
【解析】解:由旋转得,AB=AC,∠D=∠E=22°,
∴∠B=∠ACB.
∵∠BAD=90°,
∴∠B=180°﹣∠BAD﹣∠D=68°,
∴∠ACB=68°,
∴∠BAC=180°﹣∠B﹣∠ACB=44°.
故答案为:44°.
【点睛】本题考查旋转的性质,三角形内角和定理,熟练掌握旋转的性质是解答本题的关键.
15.(2024 金华一模)如图,在菱形ABCD中,点E在BC上,将△ABE沿AE折叠得到△AGE,点G在BC的延长线上,AG与CD相交于点F.若,则tanB的值为 .
【点拨】设FG=k,AF=3k,则AG=4k=AD=BC,依据△ADF∽△GCF,即可得到CG=AD=k;由折叠可得,BE=BG=k.在Rt△ABE中,依据勾股定理即可得到AE==k,进而得出tanB的值.
【解析】解:设FG=k,AF=3k,则AG=4k=AD=BC,
∵AD∥CG,
∴△ADF∽△GCF,
∴==3,
∴CG=AD=k,
∴BG=4k+k=k,
由折叠可得,BE=BG=k,∠AEB=∠AEG=90°,
∴Rt△ABE中,AE==k,
∴tanB===,
故答案为:.
【点睛】本题主要考查了菱形的性质以及折叠变换,解决问题的关键是掌握折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.
16.(2024 普陀区二模)如图,在Rt△ABC中,AC=2b,BC=2a,点D,E分别为BC、AB的中点,将△BDE绕着点B顺时针旋转,得到△BD′E′,当C,E′,D′在同一直线上时,则CE′的长为 或 .
【点拨】根据中位线的性质可求出DE的长,进而得出D′E′的长,再根据C,E′,D′在一条直线上结合勾股定理求出CD′的长即可解决问题.
【解析】解:当E′,D′在AB上方时,如图所示,
∵点D,E分别为BC、AB的中点,
∴DE是△ABC的中位线,
∴DE=,DE∥AC,
∴∠BDE=∠BCA=90°.
∵点D是BC中点,
∴BD=.
由旋转可知,
D′E′=DE=b,BD′=BD=a,∠BD′E′=∠BDE=90°.
又∵点C,E′,D′在同一直线上,
则在Rt△BD′C中,
CD′=,
∴CE′=CD′﹣D′E′=.
当D′,E′在AB下方时,如图所示,
同理可得,CE′=CD′+D′E′=.
故答案为:或.
【点睛】本题考查旋转的性质及三角形中位线定理,熟知图形旋转的性质及三角形中位线定理是解题的关键.
三.解答题
17.(2024 金华一模)如图,在边长为1的小正方形组成的网格中建立直角坐标系,小正方形的顶点为格点,△ABC与△EFG的顶点都在格点上.
(1)作△A1B1C1,使△A1B1C1与△ABC关于原点O成中心对称.
(2)已知△ABC与△EFG关于点P成中心对称,请在图中画出点P的位置,并写出该点的坐标.
【点拨】(1)根据中心对称的性质作图即可.
(2)连接AE,BF,CG,相交于点P,则点P即为所求,由图即可得出答案.
【解析】解:(1)如图,△A1B1C1即为所求.
(2)连接AE,BF,CG,相交于点P,
则△ABC与△EFG关于点P成中心对称,
即点P为所求.
由图可知,点P的坐标为(﹣3,﹣1).
【点睛】本题考查中心对称,熟练掌握中心对称的性质是解答本题的关键.
18.(2024 温岭市一模)如图,在矩形ABCD中,点E是边BC上一点,连结AE,将△ABE沿着AE折叠得到△AFE,延长EF恰好经过点D.
(1)求证:△ADF≌△DEC.
(2)若AB=6,AD=10,求△EDC的周长.
【点拨】(1)由已知得AF⊥DE,AF=AB=DC,AD∥BC,得∠ADF=∠DEC,即可得△ADF≌△DEC(AAS).
(2)由AF=AB=6,AD=10,先求得DF==8,即可得△EDC的周长=△DAF的周长=6+8+10=24.
【解析】(1)证明:∵矩形ABCD,△ABE折叠得到△AFE,
∴AF⊥DE,AF=AB=DC,
∵AD∥BC,
∴∠ADF=∠DEC,
∴△ADF≌△DEC(AAS).
(2)解:由AF=AB=6,AD=10,
得DF==8,
得△EDC的周长=△DAF的周长=6+8+10=24.
【点睛】本题主要考查了三角形全等,解题关键是正确计算.
19.(2025 衢州一模)如图,在△ABC中,CA=CB,D是△ABC内一点,连结CD,将线段CD绕点C逆时针旋转到CE,使∠DCE=∠ACB,连结AD,DE,BE.
(1)求证:△CAD≌△CBE.
(2)当∠CAB=60°时,求∠CBE与∠BAD的度数和.
【点拨】(1)由旋转得CD=CE,由题意得∠ACD=∠BCE,根据全等三角形的判定可得结论.
(2)由题意得△ABC是等边三角形,可得∠CAB=60°.由全等三角形的性质可得∠CAD=∠CBE,则∠CBE+∠BAD=∠CAD+∠BAD=∠CAB=60°.
【解析】(1)证明:由旋转得,CD=CE.
∵∠DCE=∠ACB,
∴∠DCE﹣∠DCB=∠ACB﹣∠DCB,
∴∠ACD=∠BCE.
在△ACD和△BCE中,
,
∴△ACD≌△BCE(SAS).
(2)解:∵△ACD≌△BCE,
∴∠CAD=∠CBE.
∵∠CBA=60°,CA=CB,
∴△ABC是等边三角形,
∴∠CAB=60°.
∴∠CBE+∠BAD=∠CAD+∠BAD=∠CAB=60°.
【点睛】本题考查旋转的性质、全等三角形的判定与性质,熟练掌握旋转的性质、全等三角形的判定与性质是解答本题的关键.
20.(2024 瑞安市二模)如图,在Rt△ABC中,点D是BC的中点,点E在AB上,将△BDE沿DE翻折至△FDE,使点F落在AC上,延长EF与BC的延长线交于点G.
(1)求证:DE∥AC.
(2)若BC=10,,求AC的长.
【点拨】(1)因为△BDE沿DE翻折至△FDE,点D是BC的中点,得出∠BDE=∠EDF,BD=DF=DC,则∠DFC=∠DCF,又因为∠BDE+∠EDF=∠DFC+∠DCF,推出∠EDF=∠DFC,则DE∥AC;
(2)根据DE∥AC,得出,根据BC=10,得出BD=DF=DC=5,CG=8,又因为∠DFG=∠DFE=∠B=90°,根据勾股定理求出FG,则,因为DE∥AC,且点D是BC的中点,所以点E是AB的中点,则AB=15,根据勾股定理求出AC即可.
【解析】(1)证明:∵△BDE沿DE翻折至△FDE,点D是BC的中点,
∴∠BDE=∠EDF,BD=DF=DC,
∴∠DFC=∠DCF,
又∵∠BDE+∠EDF=∠DFC+∠DCF,
∴∠EDF=∠DFC,
∴DE∥AC;
(2)解:∵DE∥AC,
∴,
∵BC=10,
∴BD=DF=DC=5,CG=8,
∵∠DFG=∠DFE=∠B=90°,
∴,
∴,
∵DE∥AC,且点D是BC的中点,
∴点E是AB的中点,
∴AB=15,
∴.
【点睛】本题考查翻折变换,平行线的判定与性质,解题的关键是掌握相关知识的灵活运用.
21.(2024 拱墅区校级二模)综合与实践
如图1是实验室中的一种机械装置,BC在地面上,所在等腰直角三角形ABC是固定支架,机械臂AD可以绕点A旋转,同时机械臂DM可以绕点D旋转,已知∠BAC=90°,AD=6,DM=2.
(1)如图2,把机械臂AD顺时针旋转90°,点D旋转到点E处,连结DE,当∠AEC=135°,
①连接CD,探究BE与CD的数量关系和位置关系,并说明理由;
②当CE=7时,求BE的长;
(2)如图3,机械臂A、D、M三点共线,AM∥BC,此时机械臂AM顺时针旋转105°,机械臂一端恰好落在BC边上,标记为点N,求支架AB的长.
【点拨】(1)①连接CD,先证明△BAE≌△CAD(AAS),则BE=CD,BE⊥CD;
②根据勾股定理求即可.
(2)过点N作NE⊥AB,根据30° 所对的边等于斜边的一半可得,构造直角三角形,即可得出结论;
【解析】解:(1)①连接CD,
由旋转可知,AE=AD,∠DAE=90°,
∵△ABC是等腰三角形,
∴AB=AC,∠BAC=90°,
∴∠BAE=∠CAD,
∴△BAE≌△CAD(AAS),
∴BE=CD,∠ABE=∠ACD,
∵∠BAC=90°,
∴∠ABE+∠CBE+∠ACB=90°,
∴∠ACD+∠CBE+∠ACB=90°,
∴BE⊥CD,
②∵AD=6,∠DAE=90°,AE=AD,
∴,∠AED=45°,
∵∠AEC=135°,
∴∠CED=90°,
∵,CE=7,
∴,
∴BE=11.
(2)过点N作NE⊥AB,
∵AM顺时针旋转105°,
∴∠MAN=105°,AM=AD+DM=AN=8,
∵AM∥BC,
∴∠MAN=∠ANB=105°,
∵NE⊥AB,
∴∠BEN=∠AEN=90°,
∵∠B=45°,
∴∠BNE=45°,BE=EN,
∴∠ANE=60°,
∴∠NAE=30°,
∴,
,
∴.
【点睛】本题考查几何变换的综合应用,熟练掌握三角形全等的判定及性质,勾股定理,旋转的性质是解题的关键.
22.(2024 上城区一模)综合与实践
主题任务 “我的校园我做主”草坪设计
入项探究环节 任务背景 学校举办“迎五一,爱劳动”主题实践活动,九(2)班参加校园美化设计任务: 校园内有一块宽为31米,长为40米的矩形草坪,在草坪上设计两条小路, 具体要求: (1)矩形草坪每条边上必须有一个口宽相等的路口; (2)两条小路必须设计成平行四边形;
驱动任务一 九(2)班各个实践小组的设计方案汇总后,主要有甲、乙、丙三种不同的方案(如图1): (1)直观猜想:方案中小路的总面积大小关系:S甲 相等 S乙,S甲 不相等 S丙;(请填“相等”或“不相等”)
深入探究 驱动任务二 验证猜想:各个实践小组用如表格进行研究: 方案纵向小路面积横向小路面积纵横交叉面积小路总面积乙方案31x40x甲方案31x40x丙方案31x40x
(2)请用含x的代数式表示甲方案中小路总面积: (71x﹣x2)平方米 ;
驱动任务三 (3)如果甲种方案除小路后草坪总面积约为1170平方米.请计算两条小路的宽度是多少?
拓展探究 驱动任务四 为了深入研究,各个小组选择丙方案(如图2)进行研究.若两条小路与矩形两组对边所夹锐角∠BGF=∠AEF=θ. (4)若θ=60°时,用含x的代数式拓表示四边形FHPQ的边长FH; (5)若x=1时,请用含θ的三角函数表示两条路重叠部分四边形FHPQ的面积,并写出sinθ取值范围.
【点拨】(1)应用平移的性质即可求得答案;
(2)根据小路总面积=横向小路面积+纵向小路面积﹣重叠部分的面积,即可得出答案;
(3)表达出草地面积,建立方程求解即可;
(4)连接FH,过点F作FM∥AD,交KH于M,由∠AEF+∠AGF=180°,得出四边形AEFG是圆内接四边形,进而可得∠A+∠EFG=180°,即∠EFG=90°,再运用解直角三角形即可求得答案;
(5)连接FM、PM、PQ、FQ,过点F作FM∥AD,交KH于M,可证得四边形FHPQ是正方形,边长为sinθ,即可得出正方形FHPQ的面积;当G与A重合时,θ最小,即sinθ的值最小,而θ为锐角,sinθ<1,即可求出答案.
【解析】解:(1)如图1,
∵S甲=40×31﹣(40﹣x)(31﹣x)=71x﹣x2,S乙=40×31﹣(40﹣x)(31﹣x)=71x﹣x2,S丙不确定,
∴S甲=S乙≠S丙,
故答案为:相等,不相等;
(2)S甲=40x+31x﹣x2=71x﹣x2(平方米),
故答案为:(71x﹣x2)平方米;
(3)由题意得:(40﹣x)(31﹣x)=1170,
解得:x1=1,x2=70(不符合题意,舍去),
答:两条小路的宽度是1米;
(4)如图2,连接FH,过点F作FM∥AD,交KH于M,
∵∠BGF=∠AEF=θ=60°,∠BGF+∠AGF=180°,
∴∠AEF+∠AGF=180°,
∴四边形AEFG是圆内接四边形,
∴∠A+∠EFG=180°,
∵∠A=90°,
∴∠EFG=90°,
∵EF∥KH,
∴∠FHM=∠EFG=90°,
∵FM∥AD,
∴∠EFM=∠AEF,
∵EF∥KH,
∴∠FMH=∠EFM,四边形EFMK是平行四边形,
∴∠FMH=∠AEF=60°,FM=EK=x,
∴FH=FM sin∠FMH=x sin60°=x(米);
(5)如图3,连接FM、PM、PQ、FQ,过点F作FM∥AD,交KH于M,
则四边形EFMK是平行四边形,
∴FM=EK=1,∠FMH=∠AEF=θ,
∵FH∥PQ,FQ∥PH,
∴四边形FHPQ是平行四边形,
由(4)知:∠AFE=90°,
∴∠QFH=90°,
∴四边形FHPQ是矩形,
在Rt△FMH中,FH=FM sinθ=sinθ,
同理可得FQ=sinθ,
∴FH=FQ,
∴四边形FHPQ是正方形,
∴两条路重叠部分四边形FHPQ的面积为sin2θ平方米;
如图4,当G与A重合时,
∵∠DAR+∠ARD=90°,∠DAR+∠AEF=90°,
∴∠ARD=∠AEF=θ,
此时θ最小,即sinθ的值最小,
∵CR=1,
∴DR=31﹣1=30,
在Rt△ADR中,AR===50,
∴sinθ===,
已知θ为锐角,
∴sinθ<1,
∴≤sinθ<1.
【点睛】本题是解直角三角形应用问题,考查了矩形的判定和性质,正方形的判定和性质,直角三角形的性质,解直角三角形等,解题关键是理解题意,熟练运用解直角三角形解决问题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
专题26 图形的轴对称、平移与旋转
一.选择题
1.(2024 滨州)数学中有许多精美的曲线,以下是“悬链线”“黄金螺旋线”“三叶玫瑰线”和“笛卡尔心形线”.其中不是轴对称图形的是( )
A. B. C. D.
2.(2024 大庆)垃圾分类功在当代,利在千秋.下列垃圾分类指引标志中,文字上方的图形既是轴对称图形又是中心对称图形的是( )
A.厨余垃圾 B.有害垃圾 C.其他垃圾 D.可回收物
3.(2024 拱墅区一模)在平面直角坐标系中,点A(2,﹣3)与点B(a,b)关于y轴对称,则( )
A.a=2,b=﹣3 B.a=2,b=3 C.a=﹣2,b=﹣3 D.a=﹣2,b=3
4.(2024 海南)平面直角坐标系中,将点A向右平移3个单位长度得到点A′(2,1),则点A的坐标是( )
A.(5,1) B.(2,4) C.(﹣1,1) D.(2,﹣2)
5.(2024 天津)如图,△ABC中,∠B=30°,将△ABC绕点C顺时针旋转60°得到△DEC,点A,B的对应点分别为D,E,延长BA交DE于点F,下列结论一定正确的是( )
A.∠ACB=∠ACD B.AC∥DE C.AB=EF D.BF⊥CE
6.(2025 沁阳市二模)如图,点A(0,﹣2),B(1,0),将线段AB平移得到线段DC,若∠ABC=90°,BC=2AB,则点D的坐标是( )
A.(4,﹣4) B.(4,﹣6) C.(6,﹣2) D.(3,﹣4)
7.(2024 鹿城区校级模拟)如图,把一张长方形纸片ABCD沿PQ,MN折叠.顶点A、B,C,D的对应点分别为A′,B′,C′,D′,点B′与D′重合,点A′恰与BC,MD′的交点重合.若CD=2,A′M=3,则AD的长为( )
A.12cm B. C. D.15cm
8.(2025 浙江模拟)如图,E,F分别是正方形ABCD的边AD,BC上的点,将正方形纸片ABCD沿EF折叠,使得点B的对应点B'恰好落在边CD上,要想知道正方形ABCD的边长,只需知道( )
A.BF的长度 B.△B′CF的周长 C.△B′DG的周长 D.△A′EG的面积
9.(2024 椒江区二模)如图,将三角形ABC(AC>AB)沿BC方向平移得到△DEF,使,DE与AC交于点M,以下关于四边形DMCF和四边形ABEM周长的说法,正确的是( )
A.周长之差可由(AC﹣AB)值确定
B.周长之和可由(AC+AB)值确定
C.周长之差可由(AC﹣AB+BC)值确定
D.周长之和可由(AC+AB+BC)值确定
10.(2024 舟山一模)如图,在Rt△ABC中,∠ACB=90°,D,E分别为BC,AB的中点,将△EDB绕点B顺时针旋转α(0<α<90°)形成△E′D′B,连结AE′.若BC=2AC,AE′∥BC时,则为( )
A. B. C. D.
二.填空题
11.(2024 海宁市三模)已知点M(a,1)与点N(﹣2,b)关于原点成中心对称,则a+b= .
12.(2024 辽宁)在平面直角坐标系中,线段AB的端点坐标分别为A(2,﹣1),B(1,0),将线段AB平移后,点A的对应点A′的坐标为(2,1),则点B的对应点B′的坐标为 .
13.(2024 新昌县一模)如图,将周长为12的△ABC沿BC边向右平移3个单位,得到△DEF,则四边形ABFD的周长为 .
14.(2024 瓯海区校级三模)如图,在△ABD中,∠BAD=90°,将△ABD绕点A逆时针旋转后得到△ACE,此时点C恰好落在BD边上.若∠E=22°,则∠BAC= .
15.(2024 金华一模)如图,在菱形ABCD中,点E在BC上,将△ABE沿AE折叠得到△AGE,点G在BC的延长线上,AG与CD相交于点F.若,则tanB的值为 .
16.(2024 普陀区二模)如图,在Rt△ABC中,AC=2b,BC=2a,点D,E分别为BC、AB的中点,将△BDE绕着点B顺时针旋转,得到△BD′E′,当C,E′,D′在同一直线上时,则CE′的长为 .
三.解答题
17.(2024 金华一模)如图,在边长为1的小正方形组成的网格中建立直角坐标系,小正方形的顶点为格点,△ABC与△EFG的顶点都在格点上.
(1)作△A1B1C1,使△A1B1C1与△ABC关于原点O成中心对称.
(2)已知△ABC与△EFG关于点P成中心对称,请在图中画出点P的位置,并写出该点的坐标.
18.(2024 温岭市一模)如图,在矩形ABCD中,点E是边BC上一点,连结AE,将△ABE沿着AE折叠得到△AFE,延长EF恰好经过点D.
(1)求证:△ADF≌△DEC.
(2)若AB=6,AD=10,求△EDC的周长.
19.(2025 衢州一模)如图,在△ABC中,CA=CB,D是△ABC内一点,连结CD,将线段CD绕点C逆时针旋转到CE,使∠DCE=∠ACB,连结AD,DE,BE.
(1)求证:△CAD≌△CBE.
(2)当∠CAB=60°时,求∠CBE与∠BAD的度数和.
20.(2024 瑞安市二模)如图,在Rt△ABC中,点D是BC的中点,点E在AB上,将△BDE沿DE翻折至△FDE,使点F落在AC上,延长EF与BC的延长线交于点G.
(1)求证:DE∥AC.
(2)若BC=10,,求AC的长.
21.(2024 拱墅区校级二模)综合与实践
如图1是实验室中的一种机械装置,BC在地面上,所在等腰直角三角形ABC是固定支架,机械臂AD可以绕点A旋转,同时机械臂DM可以绕点D旋转,已知∠BAC=90°,AD=6,DM=2.
(1)如图2,把机械臂AD顺时针旋转90°,点D旋转到点E处,连结DE,当∠AEC=135°,
①连接CD,探究BE与CD的数量关系和位置关系,并说明理由;
②当CE=7时,求BE的长;
(2)如图3,机械臂A、D、M三点共线,AM∥BC,此时机械臂AM顺时针旋转105°,机械臂一端恰好落在BC边上,标记为点N,求支架AB的长.
22.(2024 上城区一模)综合与实践
主题任务 “我的校园我做主”草坪设计
入项探究环节 任务背景 学校举办“迎五一,爱劳动”主题实践活动,九(2)班参加校园美化设计任务: 校园内有一块宽为31米,长为40米的矩形草坪,在草坪上设计两条小路, 具体要求: (1)矩形草坪每条边上必须有一个口宽相等的路口; (2)两条小路必须设计成平行四边形;
驱动任务一 九(2)班各个实践小组的设计方案汇总后,主要有甲、乙、丙三种不同的方案(如图1): (1)直观猜想:方案中小路的总面积大小关系:S甲 S乙,S甲 S丙;(请填“相等”或“不相等”)
深入探究 驱动任务二 验证猜想:各个实践小组用如表格进行研究: 方案纵向小路面积横向小路面积纵横交叉面积小路总面积乙方案31x40x甲方案31x40x丙方案31x40x
(2)请用含x的代数式表示甲方案中小路总面积: ;
驱动任务三 (3)如果甲种方案除小路后草坪总面积约为1170平方米.请计算两条小路的宽度是多少?
拓展探究 驱动任务四 为了深入研究,各个小组选择丙方案(如图2)进行研究.若两条小路与矩形两组对边所夹锐角∠BGF=∠AEF=θ. (4)若θ=60°时,用含x的代数式拓表示四边形FHPQ的边长FH; (5)若x=1时,请用含θ的三角函数表示两条路重叠部分四边形FHPQ的面积,并写出sinθ取值范围.
答案与解析
一.选择题
1.(2024 滨州)数学中有许多精美的曲线,以下是“悬链线”“黄金螺旋线”“三叶玫瑰线”和“笛卡尔心形线”.其中不是轴对称图形的是( )
A. B. C. D.
【点拨】根据轴对称图形的概念求解.
【解析】解:A、是轴对称图形;
B、不是轴对称图形;
C、是轴对称图形;
D、是轴对称图形;
故选:B.
【点睛】本题考查了轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合.
2.(2024 大庆)垃圾分类功在当代,利在千秋.下列垃圾分类指引标志中,文字上方的图形既是轴对称图形又是中心对称图形的是( )
A.厨余垃圾 B.有害垃圾 C.其他垃圾 D.可回收物
【点拨】一个平面内,如果一个图形沿一条直线折叠,若折叠后直线两旁的部分能够完全重合,那么这个图形即为轴对称图形;一个平面内,如果一个图形绕某个点旋转180°,若旋转后的图形与原来的图形完全重合,那么这个图形即为中心对称图形;据此进行判断即可.
【解析】解:A是轴对称图形,但它不是中心对称图形,则A不符合题意;
B既是轴对称图形,也是中心对称图形,则B符合题意;
C不是轴对称图形,也不是中心对称图形,则C不符合题意;
D不是轴对称图形,也不是中心对称图形,则D不符合题意;
故选:B.
【点睛】本题考查轴对称图形及中心对称图形,熟练掌握其定义是解题的关键.
3.(2024 拱墅区一模)在平面直角坐标系中,点A(2,﹣3)与点B(a,b)关于y轴对称,则( )
A.a=2,b=﹣3 B.a=2,b=3 C.a=﹣2,b=﹣3 D.a=﹣2,b=3
【点拨】根据“关于y轴对称的点,纵坐标相同,横坐标互为相反数”即可求出a、b的值.
【解析】解:在平面直角坐标系中,点A(2,﹣3)与点B(a,b)关于y轴对称,则a=﹣2,b=﹣3.
故选:C.
【点睛】本题考查了关于y轴对称的点的坐标,解决本题的关键是掌握好对称点的坐标规律:关于y轴对称的点,纵坐标相同,横坐标互为相反数.
4.(2024 海南)平面直角坐标系中,将点A向右平移3个单位长度得到点A′(2,1),则点A的坐标是( )
A.(5,1) B.(2,4) C.(﹣1,1) D.(2,﹣2)
【点拨】将点A'的横坐标减3,纵坐标不变即可得到点A的坐标.
【解析】解:将点A向右平移3个单位长度后得到点A'(2,1),
∴点A的坐标是(2﹣3,1),即点A的坐标为(﹣1,1),
故选:C.
【点睛】此题主要考查了坐标与图形变化﹣平移,关键是掌握平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.
5.(2024 天津)如图,△ABC中,∠B=30°,将△ABC绕点C顺时针旋转60°得到△DEC,点A,B的对应点分别为D,E,延长BA交DE于点F,下列结论一定正确的是( )
A.∠ACB=∠ACD B.AC∥DE C.AB=EF D.BF⊥CE
【点拨】先根据旋转性质得∠BCE=∠ACD=60°,结合∠B=30°,即可得证BF⊥CE,再根据同旁内角互补证明两直线平行,来分析AC∥DE不一定成立;根据图形性质以及角的运算或线段的运算得出A和C选项是错误的.
【解析】解:设BF与CE相交于点H,如图所示:
∵△ABC中,将△ABC绕点C顺时针旋转60°得到△DEC,
∴∠BCE=∠ACD=60°,
∵∠B=30°,
∴在△BHC中,∠BHC=180°﹣∠BCE﹣∠B=90°,
∴BF⊥CE,故D选项正确;
设∠ACH=x°,
∴∠ACB=60°﹣x°,
∵∠B=30°,
∴∠EDC=∠BAC=180°﹣30°﹣(60°﹣x°)=90°+x°,
∴∠EDC+∠ACD=90°+x°+60°=150°+x°,
∵x°不一定等于30°,
∴∠EDC+∠ACD不一定等于180°,
∴AC∥DE不一定成立,故B选项不正确;
∵∠ACB=60°﹣x°,∠ACD=60°,x°不一定等于0°,
∴∠ACB=∠ACD不一定成立,故A选项不正确;
∵将△ABC绕点C顺时针旋转60°得到△DEC,
∴AB=ED=EF+FD,
∴BA>EF,故C选项不正确;
故选:D.
【点睛】本题考查了旋转性质以及两个锐角互余的三角形是直角三角形,平行线的判定,正确掌握相关性质内容是解题的关键.
6.(2025 沁阳市二模)如图,点A(0,﹣2),B(1,0),将线段AB平移得到线段DC,若∠ABC=90°,BC=2AB,则点D的坐标是( )
A.(4,﹣4) B.(4,﹣6) C.(6,﹣2) D.(3,﹣4)
【点拨】过点D作DE⊥y轴于点E,利用点A,B的坐标表示出线段OA,OB的长,利用平移的性质和矩形的判定定理得到四边形ABCD是矩形;利用相似三角形的判定与性质求得线段DE,AE的长,进而得到OE的长,则结论可得.
【解析】解:过点D作DE⊥y轴于点E,如图,
∵点A(0,﹣2)、B(1,0),
∴OA=2,OB=1.
∵线段AB平移得到线段DC,
∴AB∥CD,AB=CD,
∴四边形ABCD是平行四边形,
∵∠ABC=90°,
∴四边形ABCD是矩形,
∴∠BAD=90°,BC=AD,
∵BC=2AB,
∴AD=2AB,
∵∠BAO+∠DAE=90°,∠BAO+∠ABO=90°,
∴∠ABO=∠EAD.
∵∠AOB=∠AED=90°,
∴△ABO∽△DAE.
∴===,
∴DE=2OA=4,AE=2OB=2,
∴OE=OA+AE=4,
∴D(4,﹣4).
故选:A.
【点睛】本题主要考查了坐标与图形变化﹣平移,矩形的判定与性质,相似三角形的判定与性质,利用点的坐标表示出相应线段的长度是解题的关键.
7.(2024 鹿城区校级模拟)如图,把一张长方形纸片ABCD沿PQ,MN折叠.顶点A、B,C,D的对应点分别为A′,B′,C′,D′,点B′与D′重合,点A′恰与BC,MD′的交点重合.若CD=2,A′M=3,则AD的长为( )
A.12cm B. C. D.15cm
【点拨】过点A'作A'E⊥C'N于点E,在Rt△A'NE中,求出A'N,A'E,NE,证明△A'QB'∽△NA'E,利用对应边成比例求出A'Q,B'Q,再利用线段间的关系即可求出BC,从而得到AD的长.
【解析】解:过点A'作A'E⊥C'N于点E,如图,
由题意,知四边形A'B'C'E是矩形,
∴A'E=D'C'=DC=2,EC'=A′B'=AB=DC=2,
∵把一张长方形纸片ABCD沿PQ,MN折叠.
∴AD∥BC,∠DMN=∠A'MN,
∴∠DMN=∠A'NM=∠A'MN,
∴A'N=A'M=3,
在Rt△A'NE中,
由勾股定理,得NE===,
由题意,知A'E∥QB',
∴∠A'QB'=∠NA'E,
又∵∠A'B'Q=∠NEA'=90°,
∴△A'QB'∽△NA'E,
∴====,
∴A'Q=NA'=×3=,
QB'=A'E=×2=,
∴BQ=QB'=,NC=NC'=NE+EC'=+2,
∴AD=BC=BQ+A'Q+A'N+NC=++3++2=,
故选:B.
【点睛】本题考查翻折变换,矩形的性质,勾股定理,相似三角形的判定和性质,弄清图形中相关线段之间的关系,掌握相关图形的性质和判定是解题的关键.
8.(2025 浙江模拟)如图,E,F分别是正方形ABCD的边AD,BC上的点,将正方形纸片ABCD沿EF折叠,使得点B的对应点B'恰好落在边CD上,要想知道正方形ABCD的边长,只需知道( )
A.BF的长度 B.△B′CF的周长 C.△B′DG的周长 D.△A′EG的面积
【点拨】证明△DB′G∽△CFB′,可得==,故DB'+DG+B'G==,即可证明DB'+DG+B'G=2AB,故要想知道正方形ABCD的边长,只需知道△B′DG的周长.
【解析】解:∵四边形ABCD是正方形,
∴∠D=∠C=∠B=90°,BC=CD=AB,
由折叠得∠GB′F=∠B=90°,B′F=BF,
∴DB′=CD﹣B′C=BC﹣B′C,CF+B′F=CF+BF=BC,BF2﹣B′C2=B′F2﹣B′C2=CF2,∠DB′G=∠CFB′=90°﹣∠CB′F,
∴△DB′G∽△CFB′,
∴==,
∴==,
∴DB'+DG+B'G==,
∵====2(BF+CF)=2AB,
∴DB'+DG+B'G=2AB,
∴要想知道正方形ABCD的边长,只需知道△B′DG的周长;
故选:C.
【点睛】本题考查折叠变化,涉及相似三角形的判定与性质,正方形性质及应用,解题的关键是需要有较强的运算,变形的能力.
9.(2024 椒江区二模)如图,将三角形ABC(AC>AB)沿BC方向平移得到△DEF,使,DE与AC交于点M,以下关于四边形DMCF和四边形ABEM周长的说法,正确的是( )
A.周长之差可由(AC﹣AB)值确定 B.周长之和可由(AC+AB)值确定
C.周长之差可由(AC﹣AB+BC)值确定 D.周长之和可由(AC+AB+BC)值确定
【点拨】根据平移的性质得出周长关系解答即可.
【解析】解:由平移可知,BE=CF,AB=DE,AC=DF,BC=EF,
∵BE=BC,
∴EC=2BE,BC=3BE,
∴四边形DMCF和四边形ABEM周长之差=(DM+MC+CF+DF)﹣(AB+BE+AM+ME)=(AB﹣ME+AC﹣AM+BE+AC)﹣(AB+BE+AM+ME)=AB﹣ME+AC﹣AM+BE+AC﹣AB﹣BE﹣AM﹣ME=2AC﹣2ME﹣2AM=,
四边形DMCF和四边形ABEM周长之和=(DM+MC+CF+DF)+(AB+BE+AM+ME)=(AB﹣ME+AC﹣AM+BE+AC)+(AB+BE+AM+ME)=2AB+2BE+2AC=2AB+BC+2AC,
∴周长之差可由(AC﹣AB)值确定,
故选:A.
【点睛】此题考查平移的性质,关键是根据平移的性质得出周长关系解答.
10.(2024 舟山一模)如图,在Rt△ABC中,∠ACB=90°,D,E分别为BC,AB的中点,将△EDB绕点B顺时针旋转α(0<α<90°)形成△E′D′B,连结AE′.若BC=2AC,AE′∥BC时,则为( )
A. B. C. D.
【点拨】根据BC=2AC,可设出BC及AC的长,过点B作AE′的垂线,垂足为M,利用勾股定理表示出E′M的长,进而可表示出AE′的长,据此可解决问题.
【解析】解:∵BC=2AC,
∴令AC=a,BC=2a.
在Rt△ABC中,
AB=.
又∵点D,E分别为BC和AB的中点,
∴BD=a,BE=.
由旋转可知,
D′E′=DE=a,BE′=BE=.
过点B作AE′的垂线,垂足为M,
∵AE′∥BC,
∴∠E′AC+∠C=180°,
又∵∠C=90°,
∴∠E′AC=90°,
∴四边形ACBM为矩形,
∴BM=AC=a,AM=BC=2a.
在Rt△BE′M中,
ME′=,
∴AE′=2a﹣,
∴.
故选:B.
【点睛】本题考查旋转的性质及三角形中位线定理,熟知图形旋转的性质是解题的关键.
二.填空题
11.(2024 海宁市三模)已知点M(a,1)与点N(﹣2,b)关于原点成中心对称,则a+b= 1 .
【点拨】关于原点成中心对称的点的横坐标互为相反数,纵坐标互为相反数,由此可得a,b的值,进而可得答案.
【解析】解:∵点M(a,1)与点N(﹣2,b)关于原点成中心对称,
∴a=2,b=﹣1,
∴a+b=2﹣1=1.
故答案为:1.
【点睛】本题考查关于原点对称的点的坐标,解题的关键是熟知关于原点成中心对称的点的横坐标互为相反数,纵坐标互为相反数.
12.(2024 辽宁)在平面直角坐标系中,线段AB的端点坐标分别为A(2,﹣1),B(1,0),将线段AB平移后,点A的对应点A′的坐标为(2,1),则点B的对应点B′的坐标为 (1,2) .
【点拨】根据点A及点A对应点的坐标,得出平移的方向和距离,据此可解决问题.
【解析】解:因为点A坐标为(2,﹣1),且平移后对应点A′的坐标为(2,1),
所以2﹣2=0,1﹣(﹣1)=2,
所以1+0=1,0+2=2,
所以点B的对应点B′的坐标为(1,2).
故答案为:(1,2).
【点睛】本题主要考查了坐标与图形变化﹣平移,熟知图形平移的性质是解题的关键.
13.(2024 新昌县一模)如图,将周长为12的△ABC沿BC边向右平移3个单位,得到△DEF,则四边形ABFD的周长为 18 .
【点拨】根据平移的性质,对应点的连线AD、CF都等于平移距离,再根据四边形ABFD的周长=△ABC的周长+AD+CF代入数据计算即可得解.
【解析】解:∵△ABC沿BC方向平移2个单位得到△DEF,
∴AD=CF=2,
∴四边形ABFD的周长
=AB+BC+DF+CF+AD
=△ABC的周长+AD+CF
=12+3+3
=18.
故答案为:18.
【点睛】本题考查了平移的性质,主要利用了对应点的连线等于平移距离,结合图形表示出四边形ABFD的周长是解题的关键.
14.(2024 瓯海区校级三模)如图,在△ABD中,∠BAD=90°,将△ABD绕点A逆时针旋转后得到△ACE,此时点C恰好落在BD边上.若∠E=22°,则∠BAC= 44° .
【点拨】由旋转得,AB=AC,∠D=∠E=22°,则∠B=∠ACB=180°﹣∠BAD﹣∠D=68°,再根据∠BAC=180°﹣∠B﹣∠ACB可得答案.
【解析】解:由旋转得,AB=AC,∠D=∠E=22°,
∴∠B=∠ACB.
∵∠BAD=90°,
∴∠B=180°﹣∠BAD﹣∠D=68°,
∴∠ACB=68°,
∴∠BAC=180°﹣∠B﹣∠ACB=44°.
故答案为:44°.
【点睛】本题考查旋转的性质,三角形内角和定理,熟练掌握旋转的性质是解答本题的关键.
15.(2024 金华一模)如图,在菱形ABCD中,点E在BC上,将△ABE沿AE折叠得到△AGE,点G在BC的延长线上,AG与CD相交于点F.若,则tanB的值为 .
【点拨】设FG=k,AF=3k,则AG=4k=AD=BC,依据△ADF∽△GCF,即可得到CG=AD=k;由折叠可得,BE=BG=k.在Rt△ABE中,依据勾股定理即可得到AE==k,进而得出tanB的值.
【解析】解:设FG=k,AF=3k,则AG=4k=AD=BC,
∵AD∥CG,
∴△ADF∽△GCF,
∴==3,
∴CG=AD=k,
∴BG=4k+k=k,
由折叠可得,BE=BG=k,∠AEB=∠AEG=90°,
∴Rt△ABE中,AE==k,
∴tanB===,
故答案为:.
【点睛】本题主要考查了菱形的性质以及折叠变换,解决问题的关键是掌握折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.
16.(2024 普陀区二模)如图,在Rt△ABC中,AC=2b,BC=2a,点D,E分别为BC、AB的中点,将△BDE绕着点B顺时针旋转,得到△BD′E′,当C,E′,D′在同一直线上时,则CE′的长为 或 .
【点拨】根据中位线的性质可求出DE的长,进而得出D′E′的长,再根据C,E′,D′在一条直线上结合勾股定理求出CD′的长即可解决问题.
【解析】解:当E′,D′在AB上方时,如图所示,
∵点D,E分别为BC、AB的中点,
∴DE是△ABC的中位线,
∴DE=,DE∥AC,
∴∠BDE=∠BCA=90°.
∵点D是BC中点,
∴BD=.
由旋转可知,
D′E′=DE=b,BD′=BD=a,∠BD′E′=∠BDE=90°.
又∵点C,E′,D′在同一直线上,
则在Rt△BD′C中,
CD′=,
∴CE′=CD′﹣D′E′=.
当D′,E′在AB下方时,如图所示,
同理可得,CE′=CD′+D′E′=.
故答案为:或.
【点睛】本题考查旋转的性质及三角形中位线定理,熟知图形旋转的性质及三角形中位线定理是解题的关键.
三.解答题
17.(2024 金华一模)如图,在边长为1的小正方形组成的网格中建立直角坐标系,小正方形的顶点为格点,△ABC与△EFG的顶点都在格点上.
(1)作△A1B1C1,使△A1B1C1与△ABC关于原点O成中心对称.
(2)已知△ABC与△EFG关于点P成中心对称,请在图中画出点P的位置,并写出该点的坐标.
【点拨】(1)根据中心对称的性质作图即可.
(2)连接AE,BF,CG,相交于点P,则点P即为所求,由图即可得出答案.
【解析】解:(1)如图,△A1B1C1即为所求.
(2)连接AE,BF,CG,相交于点P,
则△ABC与△EFG关于点P成中心对称,
即点P为所求.
由图可知,点P的坐标为(﹣3,﹣1).
【点睛】本题考查中心对称,熟练掌握中心对称的性质是解答本题的关键.
18.(2024 温岭市一模)如图,在矩形ABCD中,点E是边BC上一点,连结AE,将△ABE沿着AE折叠得到△AFE,延长EF恰好经过点D.
(1)求证:△ADF≌△DEC.
(2)若AB=6,AD=10,求△EDC的周长.
【点拨】(1)由已知得AF⊥DE,AF=AB=DC,AD∥BC,得∠ADF=∠DEC,即可得△ADF≌△DEC(AAS).
(2)由AF=AB=6,AD=10,先求得DF==8,即可得△EDC的周长=△DAF的周长=6+8+10=24.
【解析】(1)证明:∵矩形ABCD,△ABE折叠得到△AFE,
∴AF⊥DE,AF=AB=DC,
∵AD∥BC,
∴∠ADF=∠DEC,
∴△ADF≌△DEC(AAS).
(2)解:由AF=AB=6,AD=10,
得DF==8,
得△EDC的周长=△DAF的周长=6+8+10=24.
【点睛】本题主要考查了三角形全等,解题关键是正确计算.
19.(2025 衢州一模)如图,在△ABC中,CA=CB,D是△ABC内一点,连结CD,将线段CD绕点C逆时针旋转到CE,使∠DCE=∠ACB,连结AD,DE,BE.
(1)求证:△CAD≌△CBE.
(2)当∠CAB=60°时,求∠CBE与∠BAD的度数和.
【点拨】(1)由旋转得CD=CE,由题意得∠ACD=∠BCE,根据全等三角形的判定可得结论.
(2)由题意得△ABC是等边三角形,可得∠CAB=60°.由全等三角形的性质可得∠CAD=∠CBE,则∠CBE+∠BAD=∠CAD+∠BAD=∠CAB=60°.
【解析】(1)证明:由旋转得,CD=CE.
∵∠DCE=∠ACB,
∴∠DCE﹣∠DCB=∠ACB﹣∠DCB,
∴∠ACD=∠BCE.
在△ACD和△BCE中,
,
∴△ACD≌△BCE(SAS).
(2)解:∵△ACD≌△BCE,
∴∠CAD=∠CBE.
∵∠CBA=60°,CA=CB,
∴△ABC是等边三角形,
∴∠CAB=60°.
∴∠CBE+∠BAD=∠CAD+∠BAD=∠CAB=60°.
【点睛】本题考查旋转的性质、全等三角形的判定与性质,熟练掌握旋转的性质、全等三角形的判定与性质是解答本题的关键.
20.(2024 瑞安市二模)如图,在Rt△ABC中,点D是BC的中点,点E在AB上,将△BDE沿DE翻折至△FDE,使点F落在AC上,延长EF与BC的延长线交于点G.
(1)求证:DE∥AC.
(2)若BC=10,,求AC的长.
【点拨】(1)因为△BDE沿DE翻折至△FDE,点D是BC的中点,得出∠BDE=∠EDF,BD=DF=DC,则∠DFC=∠DCF,又因为∠BDE+∠EDF=∠DFC+∠DCF,推出∠EDF=∠DFC,则DE∥AC;
(2)根据DE∥AC,得出,根据BC=10,得出BD=DF=DC=5,CG=8,又因为∠DFG=∠DFE=∠B=90°,根据勾股定理求出FG,则,因为DE∥AC,且点D是BC的中点,所以点E是AB的中点,则AB=15,根据勾股定理求出AC即可.
【解析】(1)证明:∵△BDE沿DE翻折至△FDE,点D是BC的中点,
∴∠BDE=∠EDF,BD=DF=DC,
∴∠DFC=∠DCF,
又∵∠BDE+∠EDF=∠DFC+∠DCF,
∴∠EDF=∠DFC,
∴DE∥AC;
(2)解:∵DE∥AC,
∴,
∵BC=10,
∴BD=DF=DC=5,CG=8,
∵∠DFG=∠DFE=∠B=90°,
∴,
∴,
∵DE∥AC,且点D是BC的中点,
∴点E是AB的中点,
∴AB=15,
∴.
【点睛】本题考查翻折变换,平行线的判定与性质,解题的关键是掌握相关知识的灵活运用.
21.(2024 拱墅区校级二模)综合与实践
如图1是实验室中的一种机械装置,BC在地面上,所在等腰直角三角形ABC是固定支架,机械臂AD可以绕点A旋转,同时机械臂DM可以绕点D旋转,已知∠BAC=90°,AD=6,DM=2.
(1)如图2,把机械臂AD顺时针旋转90°,点D旋转到点E处,连结DE,当∠AEC=135°,
①连接CD,探究BE与CD的数量关系和位置关系,并说明理由;
②当CE=7时,求BE的长;
(2)如图3,机械臂A、D、M三点共线,AM∥BC,此时机械臂AM顺时针旋转105°,机械臂一端恰好落在BC边上,标记为点N,求支架AB的长.
【点拨】(1)①连接CD,先证明△BAE≌△CAD(AAS),则BE=CD,BE⊥CD;
②根据勾股定理求即可.
(2)过点N作NE⊥AB,根据30° 所对的边等于斜边的一半可得,构造直角三角形,即可得出结论;
【解析】解:(1)①连接CD,
由旋转可知,AE=AD,∠DAE=90°,
∵△ABC是等腰三角形,
∴AB=AC,∠BAC=90°,
∴∠BAE=∠CAD,
∴△BAE≌△CAD(AAS),
∴BE=CD,∠ABE=∠ACD,
∵∠BAC=90°,
∴∠ABE+∠CBE+∠ACB=90°,
∴∠ACD+∠CBE+∠ACB=90°,
∴BE⊥CD,
②∵AD=6,∠DAE=90°,AE=AD,
∴,∠AED=45°,
∵∠AEC=135°,
∴∠CED=90°,
∵,CE=7,
∴,
∴BE=11.
(2)过点N作NE⊥AB,
∵AM顺时针旋转105°,
∴∠MAN=105°,AM=AD+DM=AN=8,
∵AM∥BC,
∴∠MAN=∠ANB=105°,
∵NE⊥AB,
∴∠BEN=∠AEN=90°,
∵∠B=45°,
∴∠BNE=45°,BE=EN,
∴∠ANE=60°,
∴∠NAE=30°,
∴,
,
∴.
【点睛】本题考查几何变换的综合应用,熟练掌握三角形全等的判定及性质,勾股定理,旋转的性质是解题的关键.
22.(2024 上城区一模)综合与实践
主题任务 “我的校园我做主”草坪设计
入项探究环节 任务背景 学校举办“迎五一,爱劳动”主题实践活动,九(2)班参加校园美化设计任务: 校园内有一块宽为31米,长为40米的矩形草坪,在草坪上设计两条小路, 具体要求: (1)矩形草坪每条边上必须有一个口宽相等的路口; (2)两条小路必须设计成平行四边形;
驱动任务一 九(2)班各个实践小组的设计方案汇总后,主要有甲、乙、丙三种不同的方案(如图1): (1)直观猜想:方案中小路的总面积大小关系:S甲 相等 S乙,S甲 不相等 S丙;(请填“相等”或“不相等”)
深入探究 驱动任务二 验证猜想:各个实践小组用如表格进行研究: 方案纵向小路面积横向小路面积纵横交叉面积小路总面积乙方案31x40x甲方案31x40x丙方案31x40x
(2)请用含x的代数式表示甲方案中小路总面积: (71x﹣x2)平方米 ;
驱动任务三 (3)如果甲种方案除小路后草坪总面积约为1170平方米.请计算两条小路的宽度是多少?
拓展探究 驱动任务四 为了深入研究,各个小组选择丙方案(如图2)进行研究.若两条小路与矩形两组对边所夹锐角∠BGF=∠AEF=θ. (4)若θ=60°时,用含x的代数式拓表示四边形FHPQ的边长FH; (5)若x=1时,请用含θ的三角函数表示两条路重叠部分四边形FHPQ的面积,并写出sinθ取值范围.
【点拨】(1)应用平移的性质即可求得答案;
(2)根据小路总面积=横向小路面积+纵向小路面积﹣重叠部分的面积,即可得出答案;
(3)表达出草地面积,建立方程求解即可;
(4)连接FH,过点F作FM∥AD,交KH于M,由∠AEF+∠AGF=180°,得出四边形AEFG是圆内接四边形,进而可得∠A+∠EFG=180°,即∠EFG=90°,再运用解直角三角形即可求得答案;
(5)连接FM、PM、PQ、FQ,过点F作FM∥AD,交KH于M,可证得四边形FHPQ是正方形,边长为sinθ,即可得出正方形FHPQ的面积;当G与A重合时,θ最小,即sinθ的值最小,而θ为锐角,sinθ<1,即可求出答案.
【解析】解:(1)如图1,
∵S甲=40×31﹣(40﹣x)(31﹣x)=71x﹣x2,S乙=40×31﹣(40﹣x)(31﹣x)=71x﹣x2,S丙不确定,
∴S甲=S乙≠S丙,
故答案为:相等,不相等;
(2)S甲=40x+31x﹣x2=71x﹣x2(平方米),
故答案为:(71x﹣x2)平方米;
(3)由题意得:(40﹣x)(31﹣x)=1170,
解得:x1=1,x2=70(不符合题意,舍去),
答:两条小路的宽度是1米;
(4)如图2,连接FH,过点F作FM∥AD,交KH于M,
∵∠BGF=∠AEF=θ=60°,∠BGF+∠AGF=180°,
∴∠AEF+∠AGF=180°,
∴四边形AEFG是圆内接四边形,
∴∠A+∠EFG=180°,
∵∠A=90°,
∴∠EFG=90°,
∵EF∥KH,
∴∠FHM=∠EFG=90°,
∵FM∥AD,
∴∠EFM=∠AEF,
∵EF∥KH,
∴∠FMH=∠EFM,四边形EFMK是平行四边形,
∴∠FMH=∠AEF=60°,FM=EK=x,
∴FH=FM sin∠FMH=x sin60°=x(米);
(5)如图3,连接FM、PM、PQ、FQ,过点F作FM∥AD,交KH于M,
则四边形EFMK是平行四边形,
∴FM=EK=1,∠FMH=∠AEF=θ,
∵FH∥PQ,FQ∥PH,
∴四边形FHPQ是平行四边形,
由(4)知:∠AFE=90°,
∴∠QFH=90°,
∴四边形FHPQ是矩形,
在Rt△FMH中,FH=FM sinθ=sinθ,
同理可得FQ=sinθ,
∴FH=FQ,
∴四边形FHPQ是正方形,
∴两条路重叠部分四边形FHPQ的面积为sin2θ平方米;
如图4,当G与A重合时,
∵∠DAR+∠ARD=90°,∠DAR+∠AEF=90°,
∴∠ARD=∠AEF=θ,
此时θ最小,即sinθ的值最小,
∵CR=1,
∴DR=31﹣1=30,
在Rt△ADR中,AR===50,
∴sinθ===,
已知θ为锐角,
∴sinθ<1,
∴≤sinθ<1.
【点睛】本题是解直角三角形应用问题,考查了矩形的判定和性质,正方形的判定和性质,直角三角形的性质,解直角三角形等,解题关键是理解题意,熟练运用解直角三角形解决问题.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
