18.2.1 勾股定理的逆定理 提优训练 (含答案)
文档属性
| 名称 | 18.2.1 勾股定理的逆定理 提优训练 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 225.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-15 12:48:34 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
18.2 勾股定理的逆定理
第 1课时 勾股定理的逆定理
1.若a,b,c 是直角三角形的三条边,下列说法正确的是( ).
A. a ,b ,c 能组成三角形
B. 3a,3b,3c能组成直角三角形
C. a+3,b+4,c+5能组成直角三角形
D. 3a,4b,5c 能组成直角三角形
2. 下列条件中,不能判断△ABC 为直角三角形的是( ).
A. a=1.5,b=2,c=2.5
B. a:b:c=5:12:13
C. ∠A+∠B=∠C
D. ∠A:∠B:∠C=3:4:5
3.三角形的三边长分别为a +b ,2ab,a -b (a,b都是正整数),则这个三角形是( ).
A.直角三角形 B.钝角三角形
C.锐角三角形 D.不能确定
4.以三角形的三边为边分别向外作正方形,正方形的面积分别是5,4,9,则此三角形的形状是( ).
A.锐角三角形 B.直角三角形
C.钝角三角形 D.任意三角形
5. 如图,在△ABC中,AB=4,BC=2,DB=1,CD= 则AC= .
6.已知a,b,c为三个正整数,如果a+b+c=12,那么以a,b,c为边能组成的三角形是:①等腰三角形;②等边三角形;③直角三角形;④钝角三角形.以上符合条件的正确结论是 .(填序号)
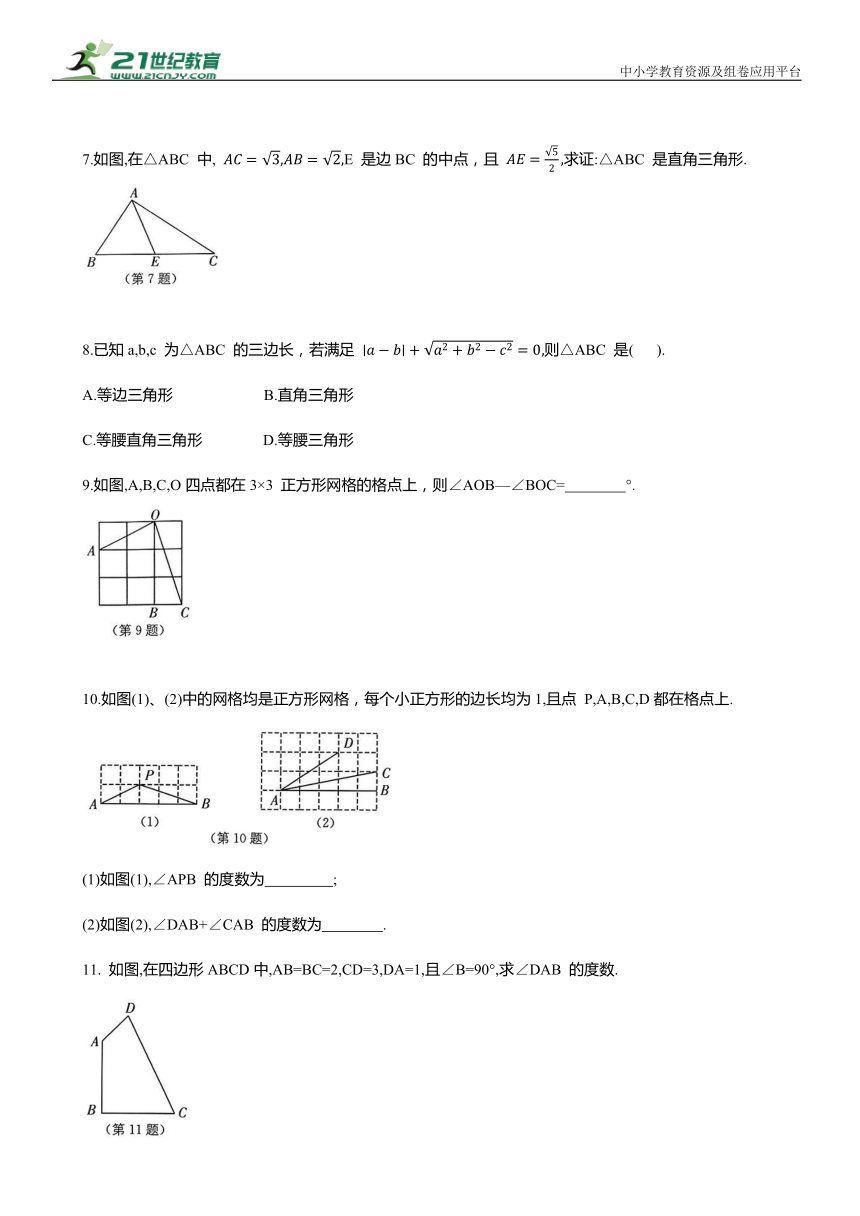
7.如图,在△ABC 中, E 是边BC 的中点,且 求证:△ABC 是直角三角形.
8.已知a,b,c 为△ABC 的三边长,若满足 则△ABC 是( ).
A.等边三角形 B.直角三角形
C.等腰直角三角形 D.等腰三角形
9.如图,A,B,C,O四点都在3×3 正方形网格的格点上,则∠AOB—∠BOC= °.
10.如图(1)、(2)中的网格均是正方形网格,每个小正方形的边长均为1,且点 P,A,B,C,D都在格点上.
(1)如图(1),∠APB 的度数为 ;
(2)如图(2),∠DAB+∠CAB 的度数为 .
11. 如图,在四边形ABCD中,AB=BC=2,CD=3,DA=1,且∠B=90°,求∠DAB 的度数.
12.阅读下列解题过程:
已知a,b,c 为△ABC 的三边长,且满足 试判断△ABC 的形状.
解:因为 ①
所以 )
所以 ③
所以△ABC 是直角三角形.
回答下列问题:
(1)上述解题过程,从哪一步开始出现错误 请写出该步序号为 .
(2)错误的原因为 .
(3)请你将正确的解答过程写下来.
13.如图,四边形 ABCD 的四个顶点都在网格上,且每个小正方形的边长都为1.
(1)BC= ,AD= ,连接BD,判断△ABD 的形状为 三角形;
(2)求四边形 ABCD 的面积.
14.如图,方格纸中的每个小正方形的边长均为1,小正方形的顶点称为格点.已知点 A,B,C都是格点.
(1)小健发现∠ABC 是直角,请补全他的解题思路;
小健的解题思路:先利用勾股定理求出△ABC的三条边长,可得 AC= ,从而可得AB,BC,AC 之间的数量关系是 ,根据 ,可得∠ABC是直角.
(2)请用一种不同于小健的方法证明∠ABC是直角.
15.三角形的周长为38,第一条边长为a,第二条边长比第一条边长的2倍多3.
(1)表示第三条边.
(2)若此三角形为等腰三角形,求a 的值.
(3)若a 为正整数,此三角形能否为直角三角形 说明理由.
16. 在△ABC中,BC=a,AC=b,AB=c,如图(1),若∠C=90°,则有 ;若△ABC 为锐角三角形,小明猜想: 理由如下:
如图(2),过点 A 作AD⊥CB 于点D.
设CD=x,
在Rt△ADC中,
在Rt△ADB 中,
即
∵a>0,x>0,∴2ax>0,∴a +b >c ,
∴当△ABC 为锐角三角形时,
∴小明的猜想是正确的.
(1)请你猜想,当△ABC 为钝角三角形时, 与c 的大小关系(如图(3));
(2)证明你猜想的结论是否正确.
第1课时 勾股定理的逆定理
1. B [解析]∵a,b,c是直角三角形的三条边,不妨设c为斜边, ∴3a,3b,3c能组成直角三角形,a ,b ,c 不能组成三角形,其他情况都不能得到直角三角形.故选 B.
2. D [解析]因为 符合勾股定理的逆定理,所以△ABC为直角三角形,选项 A不符合题意;因为a:b:c=5:12:13,所以可设a=5x,b=12x,c=13x,则( 因此△ABC 为直角三角形,选项 B不符合题意;因为∠A+∠B=∠C,∠A+∠B+∠C=180°,则∠C=90°,因此△ABC 为直角三角形,选项C不符合题意;因为∠A:∠B:∠C=3:4:5,所以设∠A=3x,则∠B=4x,∠C=5x,故3x+4x+5x=180°,解得x=15°,3x=15°×3=45°,4x=15°×4=60°,5x= ,因此△ABC 是锐角三角形,选项 D符合题意.故选 D.
解后反思 本题考查了勾股定理的逆定理、三角形的内角和定理,根据勾股定理的逆定理、三角形的内角和定理结合解方程依次判断即可.
3. A [解析]∵ ∴该三角形为直角三角形.故选 A.
4. B [解析]∵正方形的面积分别是5,4,9,
∴三角形的边长分别为 ,2,3.
∴此三角形是直角三角形.故选 B.
5.2 [解析]∵BC=2,DB=1,CD= ,∴BD +CD =BC ,∴△CDB 是直角三角形,∴∠CDB=90°,∴∠ADC=90°,在 Rt△ACD 中,由勾股定理,得
6.①②③ [解析]因为a,b,c是三个正整数,且a+b+c=12,因此能构成三角形边长的所有a,b,c的情况如下:2,5,5;4,4,4;3,4,5,依次是等腰三角形、等边三角形、直角三角形.故符合条件的正确结论是①②③.
关键提醒本题综合考查了三角形的三边关系、勾股定理的逆定理等知识,因为题意只给出了三角形三边长的和,需要学生解答时分类讨论可能的三角形形状.根据a,b,c是三个正整数,且a+b+c=12,分情况讨论得出解答.
7.如图,过点C作CF∥AB交AE 的延长线于点F.
∵E是边BC 的中点,∴BE=CE.
∵CF∥AB,∴∠B=∠ECF.
在△AEB 与△FEC中,
∴△AEB≌△FEC(ASA),
∴△AFC 是直角三角形,且∠ACF=90°.
∵AB∥CF,∴∠CAB=180°-∠ACF=90°.
∴△ABC 是直角三角形.
8. C [解析]·.
∴△ABC 是等腰直角三角形.故选 C.
9.45 [解析]如图,找到C 点关于OB 的对称点D,连接OD,AD,则∠DOB=∠COB,∠AOB-∠BOC=∠AOB-∠BOD=∠AOD.
∴△DAO 是等腰直角三角形,
∴∠AOD=45°,即∠AOB-∠BOC=45°.
■归纳总结 本题主要考查了轴对称、勾股定理和勾股定理的逆定理、等腰直角三角形的性质,得出∠AOB-∠BOC=∠AOD 是解题关键.
10.(1)135° (2)45° [解析](1)如图(1),延长 AP 交格点于点M,连接BM,
则 ∴PM +BM =PB ,∴△PMB 是等腰直角三角形,且∠PMB=90°,∴∠MPB=∠MBP =45°,
(2)如图(2),作点 C 关于AB 的对称点E,连接DE,AE,∴∠CAB=∠BAE.
由勾股定理,得
∴△ADE 是等腰直角三角形,且∠ADE=90°,
∴∠DAE=∠DEA=45°,∴∠DAB+∠CAB=∠DAB+∠BAE=∠DAE=45°.
归纳总结 本题考查了勾股定理及其逆定理的应用、等腰直角三角形的判定和性质等知识,熟练掌握勾股定理及其逆定理是解题的关键.
11.如图,连接AC.
∵∠B=90°,AB=BC=2,
∠BAC=45°.
∵CD=3,DA =1,∴AC +
)是直角三角形,
∴∠CAD=90°,∴∠DAB=45°+90°=135°.
故∠DAB的度数为135°.
12.(1)③
(2)忽略了 的可能
或 则a=b或(
∴△ABC 是等腰三角形或直角三角形或等腰直角三角形.
■方法诠释 本题考查整式的运算、勾股定理的逆定理的应用、分类讨论.判断三角形是否为直角三角形,根据三角形三边的长,利用勾股定理的逆定理加以判断即可.
等腰直角 [解析]如图,根据勾股定理,得
∴△ABD是直角三角形.
∵AD=BD,∴△ABD 是等腰直角三角形.
(2)根据勾股定理,得
∴△BCD 是直角三角形,
∴四边形ABCD 的面积
勾股定理的逆定理
(2)如图,连接AD,BD,BE,CE.
由 题 意, 得 ∠ADB =∠CEB=90°,AD=BE,BD=CE,
∴△ADB≌△BEC(SAS),
∴∠BAD=∠CBE.
∵∠ADB=90°,∴∠DAB+∠ABD=90°,
∴∠ABD+∠CBE=90°,
∴∠ABC=180°-(∠ABD+∠CBE)=90°,
∴∠ABC是直角.
解后反思 本题考查了勾股定理的逆定理、勾股定理、全等三角形的判定与性质,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
15.(1)由题意,得第二条边长为2a+3,则第三条边长为38-a-(2a+3)=35-3a.
(2)由三边关系可知,
解得
∵a≠2a+3,∴分两种情况:
①当a=35-3a,即 时,不符合三边关系,舍去;
②当2a+3=35-3a,即 时,符合三边关系,
(3)此三角形不能为直角三角形.理由如下: 且a为整数,∴a=6或7.
当a=6时,三边长为6,15,17, 不是直角三角形;当a=7时,三边长为7,17,14,7 + ,不是直角三角形.
思路引导本题根据三角形的三边关系构建不等式组,求出a 的取值范围,根据等腰三角形的性质分类构建方程,求出a的值,运用勾股定理的逆定理判断此三角形是否为直角三角形.
16.(1)当△ABC 为钝角三角形时, 与c 的大小关系为
(2)如图,过点A 作AD⊥BC交BC 的延长线于点 D,设CD=x.
在Rt△ADC中,
在Rt△ADB 中,
∵a>0,x>0,∴2ax>0,∴a +b故当△ABC为钝角三角形时,
18.2 勾股定理的逆定理
第 1课时 勾股定理的逆定理
1.若a,b,c 是直角三角形的三条边,下列说法正确的是( ).
A. a ,b ,c 能组成三角形
B. 3a,3b,3c能组成直角三角形
C. a+3,b+4,c+5能组成直角三角形
D. 3a,4b,5c 能组成直角三角形
2. 下列条件中,不能判断△ABC 为直角三角形的是( ).
A. a=1.5,b=2,c=2.5
B. a:b:c=5:12:13
C. ∠A+∠B=∠C
D. ∠A:∠B:∠C=3:4:5
3.三角形的三边长分别为a +b ,2ab,a -b (a,b都是正整数),则这个三角形是( ).
A.直角三角形 B.钝角三角形
C.锐角三角形 D.不能确定
4.以三角形的三边为边分别向外作正方形,正方形的面积分别是5,4,9,则此三角形的形状是( ).
A.锐角三角形 B.直角三角形
C.钝角三角形 D.任意三角形
5. 如图,在△ABC中,AB=4,BC=2,DB=1,CD= 则AC= .
6.已知a,b,c为三个正整数,如果a+b+c=12,那么以a,b,c为边能组成的三角形是:①等腰三角形;②等边三角形;③直角三角形;④钝角三角形.以上符合条件的正确结论是 .(填序号)
7.如图,在△ABC 中, E 是边BC 的中点,且 求证:△ABC 是直角三角形.
8.已知a,b,c 为△ABC 的三边长,若满足 则△ABC 是( ).
A.等边三角形 B.直角三角形
C.等腰直角三角形 D.等腰三角形
9.如图,A,B,C,O四点都在3×3 正方形网格的格点上,则∠AOB—∠BOC= °.
10.如图(1)、(2)中的网格均是正方形网格,每个小正方形的边长均为1,且点 P,A,B,C,D都在格点上.
(1)如图(1),∠APB 的度数为 ;
(2)如图(2),∠DAB+∠CAB 的度数为 .
11. 如图,在四边形ABCD中,AB=BC=2,CD=3,DA=1,且∠B=90°,求∠DAB 的度数.
12.阅读下列解题过程:
已知a,b,c 为△ABC 的三边长,且满足 试判断△ABC 的形状.
解:因为 ①
所以 )
所以 ③
所以△ABC 是直角三角形.
回答下列问题:
(1)上述解题过程,从哪一步开始出现错误 请写出该步序号为 .
(2)错误的原因为 .
(3)请你将正确的解答过程写下来.
13.如图,四边形 ABCD 的四个顶点都在网格上,且每个小正方形的边长都为1.
(1)BC= ,AD= ,连接BD,判断△ABD 的形状为 三角形;
(2)求四边形 ABCD 的面积.
14.如图,方格纸中的每个小正方形的边长均为1,小正方形的顶点称为格点.已知点 A,B,C都是格点.
(1)小健发现∠ABC 是直角,请补全他的解题思路;
小健的解题思路:先利用勾股定理求出△ABC的三条边长,可得 AC= ,从而可得AB,BC,AC 之间的数量关系是 ,根据 ,可得∠ABC是直角.
(2)请用一种不同于小健的方法证明∠ABC是直角.
15.三角形的周长为38,第一条边长为a,第二条边长比第一条边长的2倍多3.
(1)表示第三条边.
(2)若此三角形为等腰三角形,求a 的值.
(3)若a 为正整数,此三角形能否为直角三角形 说明理由.
16. 在△ABC中,BC=a,AC=b,AB=c,如图(1),若∠C=90°,则有 ;若△ABC 为锐角三角形,小明猜想: 理由如下:
如图(2),过点 A 作AD⊥CB 于点D.
设CD=x,
在Rt△ADC中,
在Rt△ADB 中,
即
∵a>0,x>0,∴2ax>0,∴a +b >c ,
∴当△ABC 为锐角三角形时,
∴小明的猜想是正确的.
(1)请你猜想,当△ABC 为钝角三角形时, 与c 的大小关系(如图(3));
(2)证明你猜想的结论是否正确.
第1课时 勾股定理的逆定理
1. B [解析]∵a,b,c是直角三角形的三条边,不妨设c为斜边, ∴3a,3b,3c能组成直角三角形,a ,b ,c 不能组成三角形,其他情况都不能得到直角三角形.故选 B.
2. D [解析]因为 符合勾股定理的逆定理,所以△ABC为直角三角形,选项 A不符合题意;因为a:b:c=5:12:13,所以可设a=5x,b=12x,c=13x,则( 因此△ABC 为直角三角形,选项 B不符合题意;因为∠A+∠B=∠C,∠A+∠B+∠C=180°,则∠C=90°,因此△ABC 为直角三角形,选项C不符合题意;因为∠A:∠B:∠C=3:4:5,所以设∠A=3x,则∠B=4x,∠C=5x,故3x+4x+5x=180°,解得x=15°,3x=15°×3=45°,4x=15°×4=60°,5x= ,因此△ABC 是锐角三角形,选项 D符合题意.故选 D.
解后反思 本题考查了勾股定理的逆定理、三角形的内角和定理,根据勾股定理的逆定理、三角形的内角和定理结合解方程依次判断即可.
3. A [解析]∵ ∴该三角形为直角三角形.故选 A.
4. B [解析]∵正方形的面积分别是5,4,9,
∴三角形的边长分别为 ,2,3.
∴此三角形是直角三角形.故选 B.
5.2 [解析]∵BC=2,DB=1,CD= ,∴BD +CD =BC ,∴△CDB 是直角三角形,∴∠CDB=90°,∴∠ADC=90°,在 Rt△ACD 中,由勾股定理,得
6.①②③ [解析]因为a,b,c是三个正整数,且a+b+c=12,因此能构成三角形边长的所有a,b,c的情况如下:2,5,5;4,4,4;3,4,5,依次是等腰三角形、等边三角形、直角三角形.故符合条件的正确结论是①②③.
关键提醒本题综合考查了三角形的三边关系、勾股定理的逆定理等知识,因为题意只给出了三角形三边长的和,需要学生解答时分类讨论可能的三角形形状.根据a,b,c是三个正整数,且a+b+c=12,分情况讨论得出解答.
7.如图,过点C作CF∥AB交AE 的延长线于点F.
∵E是边BC 的中点,∴BE=CE.
∵CF∥AB,∴∠B=∠ECF.
在△AEB 与△FEC中,
∴△AEB≌△FEC(ASA),
∴△AFC 是直角三角形,且∠ACF=90°.
∵AB∥CF,∴∠CAB=180°-∠ACF=90°.
∴△ABC 是直角三角形.
8. C [解析]·.
∴△ABC 是等腰直角三角形.故选 C.
9.45 [解析]如图,找到C 点关于OB 的对称点D,连接OD,AD,则∠DOB=∠COB,∠AOB-∠BOC=∠AOB-∠BOD=∠AOD.
∴△DAO 是等腰直角三角形,
∴∠AOD=45°,即∠AOB-∠BOC=45°.
■归纳总结 本题主要考查了轴对称、勾股定理和勾股定理的逆定理、等腰直角三角形的性质,得出∠AOB-∠BOC=∠AOD 是解题关键.
10.(1)135° (2)45° [解析](1)如图(1),延长 AP 交格点于点M,连接BM,
则 ∴PM +BM =PB ,∴△PMB 是等腰直角三角形,且∠PMB=90°,∴∠MPB=∠MBP =45°,
(2)如图(2),作点 C 关于AB 的对称点E,连接DE,AE,∴∠CAB=∠BAE.
由勾股定理,得
∴△ADE 是等腰直角三角形,且∠ADE=90°,
∴∠DAE=∠DEA=45°,∴∠DAB+∠CAB=∠DAB+∠BAE=∠DAE=45°.
归纳总结 本题考查了勾股定理及其逆定理的应用、等腰直角三角形的判定和性质等知识,熟练掌握勾股定理及其逆定理是解题的关键.
11.如图,连接AC.
∵∠B=90°,AB=BC=2,
∠BAC=45°.
∵CD=3,DA =1,∴AC +
)是直角三角形,
∴∠CAD=90°,∴∠DAB=45°+90°=135°.
故∠DAB的度数为135°.
12.(1)③
(2)忽略了 的可能
或 则a=b或(
∴△ABC 是等腰三角形或直角三角形或等腰直角三角形.
■方法诠释 本题考查整式的运算、勾股定理的逆定理的应用、分类讨论.判断三角形是否为直角三角形,根据三角形三边的长,利用勾股定理的逆定理加以判断即可.
等腰直角 [解析]如图,根据勾股定理,得
∴△ABD是直角三角形.
∵AD=BD,∴△ABD 是等腰直角三角形.
(2)根据勾股定理,得
∴△BCD 是直角三角形,
∴四边形ABCD 的面积
勾股定理的逆定理
(2)如图,连接AD,BD,BE,CE.
由 题 意, 得 ∠ADB =∠CEB=90°,AD=BE,BD=CE,
∴△ADB≌△BEC(SAS),
∴∠BAD=∠CBE.
∵∠ADB=90°,∴∠DAB+∠ABD=90°,
∴∠ABD+∠CBE=90°,
∴∠ABC=180°-(∠ABD+∠CBE)=90°,
∴∠ABC是直角.
解后反思 本题考查了勾股定理的逆定理、勾股定理、全等三角形的判定与性质,根据题目的已知条件并结合图形添加适当的辅助线是解题的关键.
15.(1)由题意,得第二条边长为2a+3,则第三条边长为38-a-(2a+3)=35-3a.
(2)由三边关系可知,
解得
∵a≠2a+3,∴分两种情况:
①当a=35-3a,即 时,不符合三边关系,舍去;
②当2a+3=35-3a,即 时,符合三边关系,
(3)此三角形不能为直角三角形.理由如下: 且a为整数,∴a=6或7.
当a=6时,三边长为6,15,17, 不是直角三角形;当a=7时,三边长为7,17,14,7 + ,不是直角三角形.
思路引导本题根据三角形的三边关系构建不等式组,求出a 的取值范围,根据等腰三角形的性质分类构建方程,求出a的值,运用勾股定理的逆定理判断此三角形是否为直角三角形.
16.(1)当△ABC 为钝角三角形时, 与c 的大小关系为
(2)如图,过点A 作AD⊥BC交BC 的延长线于点 D,设CD=x.
在Rt△ADC中,
在Rt△ADB 中,
∵a>0,x>0,∴2ax>0,∴a +b
