巧用勾股定理的逆定理专题提优特训8 提优训练 (含答案)
文档属性
| 名称 | 巧用勾股定理的逆定理专题提优特训8 提优训练 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 212.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-15 12:50:22 | ||
图片预览

文档简介
中小学教育资源及组卷应用平台
巧用勾股定理的逆定理专题提优特训8
题型1 用于判断三角形的形状
1.在△ABC中,内角∠A,∠B,∠C 所对的边分别为a,b,c.若
求证:△ABC 是直角三角形.
2.如图,在正方形网格中(每个小正方形的边长都是一个单位长度),建立如图所示的平面直角坐标系.
(1)在图中描出A(2,-2),B(-4,6),C(6,1),连接AB,BC,AC,试判断△ABC的形状;
(2)求△ABC 的面积.
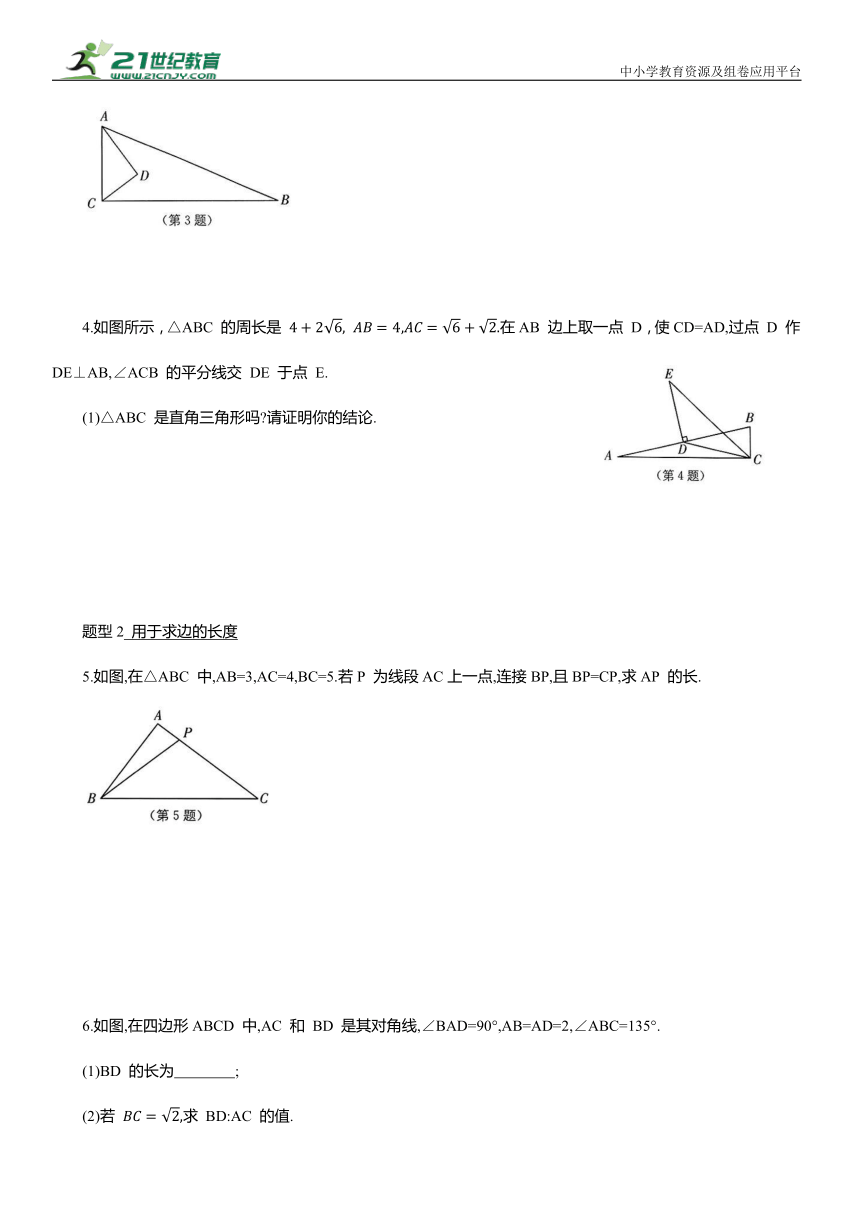
3.如图,△ABC 内部有一点 D,且∠ADC=90°,AB =13,BC=12,AD=4,CD=3.
(1)判断△ABC 的形状;
(2)求四边形 ABCD 的面积.
4.如图所示,△ABC 的周长是 在AB 边上取一点 D,使CD=AD,过点 D 作 DE⊥AB,∠ACB 的平分线交 DE 于点 E.
(1)△ABC 是直角三角形吗 请证明你的结论.
题型2 用于求边的长度
5.如图,在△ABC 中,AB=3,AC=4,BC=5.若P 为线段AC上一点,连接BP,且BP=CP,求AP 的长.
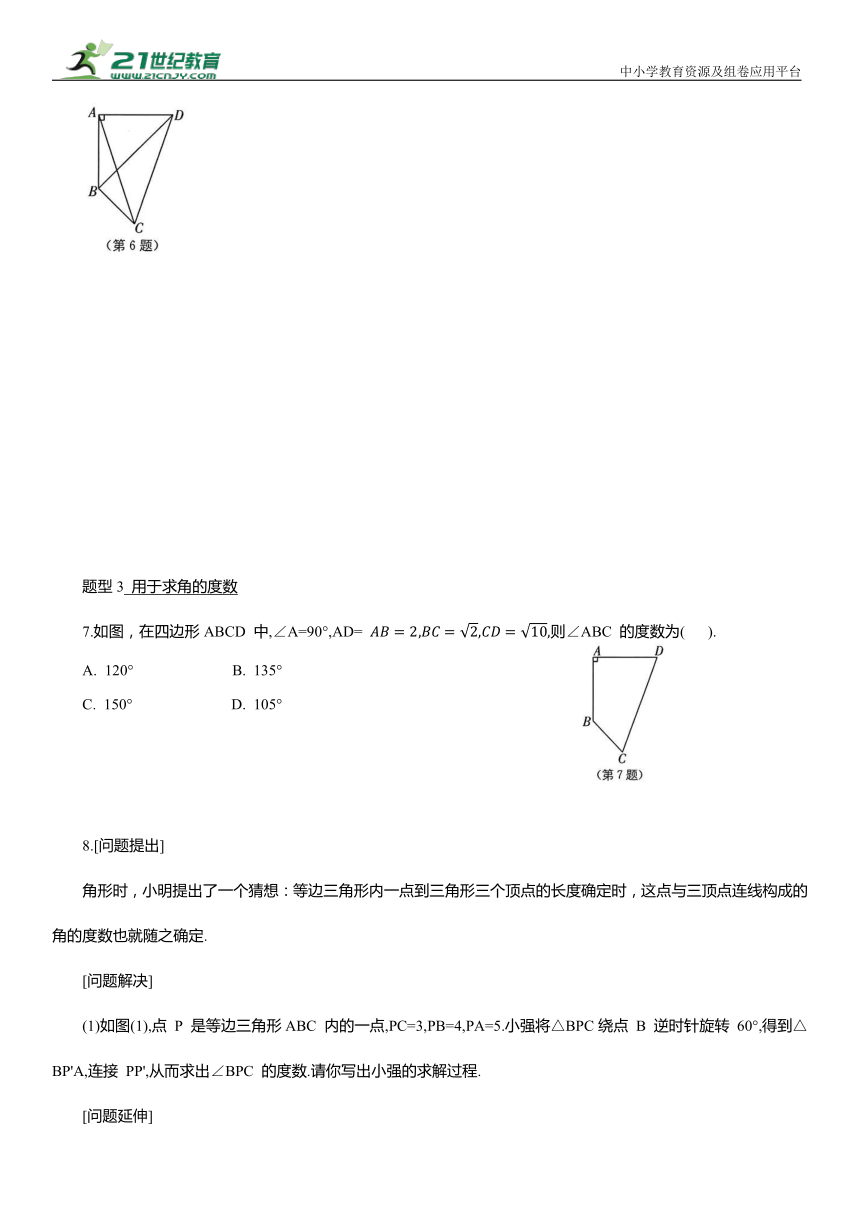
6.如图,在四边形ABCD 中,AC 和 BD 是其对角线,∠BAD=90°,AB=AD=2,∠ABC=135°.
(1)BD 的长为 ;
(2)若 求 BD:AC 的值.
题型3 用于求角的度数
7.如图,在四边形ABCD 中,∠A=90°,AD= 则∠ABC 的度数为( ).
A. 120° B. 135°
C. 150° D. 105°
8.[问题提出]
角形时,小明提出了一个猜想:等边三角形内一点到三角形三个顶点的长度确定时,这点与三顶点连线构成的角的度数也就随之确定.
[问题解决]
(1)如图(1),点 P 是等边三角形ABC 内的一点,PC=3,PB=4,PA=5.小强将△BPC绕点 B 逆时针旋转 60°,得到△BP'A,连接 PP',从而求出∠BPC 的度数.请你写出小强的求解过程.
[问题延伸]
(2)在研究中,小东又提出一个猜想:当点在等边三角形外与三顶点距离确定时,这点与三顶点连线构成的角的度数也会随之确定.如图(2),PC=3,PB=4,PA=5,求∠BPC 的度数.
[拓展应用]
(3)如图(3),在正方形 ABCD 内有一点 P, ,求∠BPC 的度数.
1.由题可知 整理,得( 即 所以△ABC 是直角三角形.
2.(1)如图.
则
∴△ABC 是直角三角形.
(2)由(1)可知, 则
归纳总结 本题考查的是勾股定理的逆定理、坐标与图形性质,能够用平面内两点的坐标求这两点之间的距离和运用勾股定理的逆定理判断三角形的形状是解题的关键.
3.(1)∵∠ADC=90°,AD=4,CD=3,
∴在△ADC 中,根据勾股定理,得
∵AB=13,BC=12,
根据勾股定理逆定理可知,△ABC 是直角三角形.
(2)四边形ABCD 的面积
故四边形ABCD 面积为24.
4.(1)△ABC 是直角三角形.证明如下:
∴△ABC 是直角三角形.
(2)如图,过点C作CH⊥AB于点H,连接EH,
∵DE⊥AB,CH⊥AB,
∴DE∥CH,∴∠DEC=∠HCE.
∵∠B+∠A=90°,∠B+∠HCB=90°,
∴∠A=∠HCB.
∵AD=CD,∴∠A=∠ACD,
∴∠HCB=∠ACD.
∵CE平分∠ACB,∴∠ACE=∠BCE,
∴∠HCE=∠DCE,∴∠DEC=∠DCE,
∴CD=AD=DE.
在Rt△ACH 中, 在Rt△DCH 中,( 解得CD=2,
5.∵AB=3,AC=4,BC=5,3 +4 =5 ,
∴△ABC 是直角三角形,且∠A=90°,
∴在 Rt△ABP 中,
∵BP=CP,AP+CP=AC=4,AB=3,
6.(1)2 [解析]∵∠BAD=90°,AB=AD=2,
(2)如图,过点C作CE⊥AB交AB的延长线于点 E.
∵∠ABC=135°,
∴△BCE 是等腰直角三角形.
∴AE=AB+BE=3,
思路引导本题考查了勾股定理及等腰直角三角形的性质及判定,解决本题的关键是熟练掌握用勾股定理解决问题.(1)由勾股定理直接求出 BD 的长;
(2)过点C 作CE⊥AB交AB 的延长线于点E.先证明△BCE 是等腰直角三角形,再用勾股定理求出AC的长,最后求出 BD: AC.
7. B [解析]如图,连接BD.
∵∠A=90°,AD=AB=2,
∴∠ABD=∠ADB=45°,BD =8.
∴△BCD 是直角三角形,∠DBC=90°,
∴∠ABC=∠ABD+∠DBC=45°+90°=135°,即∠ABC 的度数是135°.故选 B.
■方法诠释 本题考查勾股定理和勾股定理逆定理的应用,因为求解的是角的度数,先根据等腰直角三角形得到∠ABD 的度数,然后利用勾股定理逆定理判定△BCD 是直角三角形来确定∠DBC 的度数,所以根据勾股定理确定BD 值时,不需要开方求出BD的确定值,只需要知道BD 的平方值即可.
8.(1)∵△BPC 绕点 B 逆时针旋转60°得到△BP'A,∴∠P'BP=60°,BP=BP',PC=P'A,∠BPC=∠BP'A,∴△P'BP 为等边三角形,
又PC=3,PB=4,PA=5,
∴P'A=PC=3,P'P=BP=4.
∴△P'PA 为直角三角形,
(2)如图(1),将△BPC 绕点B逆时针旋转 60°得到△BP'A,则∠P'BP =60°,BP =BP',PC=P'A,∠BPC=∠BP'A,
∴△P'BP 为等边三角形,
P'P=BP.
又PC=3,PB=4,PA=5,
∴△P'PA 为直角三角形,
∴∠BPC=∠BP'A=∠PP'A-∠BP'P=90°-
(3)如图(2),将△BPC 绕点 B 逆时针旋转90°得到△BEA,连接PE,
则∠PBE = 90°, BP = BE, PC = EA, ∠BPC=∠BEA,
∴△EBP 为等腰直角三角形,
∴∠BEP=∠BPE=45°.
又PC=3,∴EA=PC=3,
∴△EPA 为直角三角形,∠PEA=90°,
∴∠BPC=∠BEA =∠BEP +∠PEA =45°+
巧用勾股定理的逆定理专题提优特训8
题型1 用于判断三角形的形状
1.在△ABC中,内角∠A,∠B,∠C 所对的边分别为a,b,c.若
求证:△ABC 是直角三角形.
2.如图,在正方形网格中(每个小正方形的边长都是一个单位长度),建立如图所示的平面直角坐标系.
(1)在图中描出A(2,-2),B(-4,6),C(6,1),连接AB,BC,AC,试判断△ABC的形状;
(2)求△ABC 的面积.
3.如图,△ABC 内部有一点 D,且∠ADC=90°,AB =13,BC=12,AD=4,CD=3.
(1)判断△ABC 的形状;
(2)求四边形 ABCD 的面积.
4.如图所示,△ABC 的周长是 在AB 边上取一点 D,使CD=AD,过点 D 作 DE⊥AB,∠ACB 的平分线交 DE 于点 E.
(1)△ABC 是直角三角形吗 请证明你的结论.
题型2 用于求边的长度
5.如图,在△ABC 中,AB=3,AC=4,BC=5.若P 为线段AC上一点,连接BP,且BP=CP,求AP 的长.
6.如图,在四边形ABCD 中,AC 和 BD 是其对角线,∠BAD=90°,AB=AD=2,∠ABC=135°.
(1)BD 的长为 ;
(2)若 求 BD:AC 的值.
题型3 用于求角的度数
7.如图,在四边形ABCD 中,∠A=90°,AD= 则∠ABC 的度数为( ).
A. 120° B. 135°
C. 150° D. 105°
8.[问题提出]
角形时,小明提出了一个猜想:等边三角形内一点到三角形三个顶点的长度确定时,这点与三顶点连线构成的角的度数也就随之确定.
[问题解决]
(1)如图(1),点 P 是等边三角形ABC 内的一点,PC=3,PB=4,PA=5.小强将△BPC绕点 B 逆时针旋转 60°,得到△BP'A,连接 PP',从而求出∠BPC 的度数.请你写出小强的求解过程.
[问题延伸]
(2)在研究中,小东又提出一个猜想:当点在等边三角形外与三顶点距离确定时,这点与三顶点连线构成的角的度数也会随之确定.如图(2),PC=3,PB=4,PA=5,求∠BPC 的度数.
[拓展应用]
(3)如图(3),在正方形 ABCD 内有一点 P, ,求∠BPC 的度数.
1.由题可知 整理,得( 即 所以△ABC 是直角三角形.
2.(1)如图.
则
∴△ABC 是直角三角形.
(2)由(1)可知, 则
归纳总结 本题考查的是勾股定理的逆定理、坐标与图形性质,能够用平面内两点的坐标求这两点之间的距离和运用勾股定理的逆定理判断三角形的形状是解题的关键.
3.(1)∵∠ADC=90°,AD=4,CD=3,
∴在△ADC 中,根据勾股定理,得
∵AB=13,BC=12,
根据勾股定理逆定理可知,△ABC 是直角三角形.
(2)四边形ABCD 的面积
故四边形ABCD 面积为24.
4.(1)△ABC 是直角三角形.证明如下:
∴△ABC 是直角三角形.
(2)如图,过点C作CH⊥AB于点H,连接EH,
∵DE⊥AB,CH⊥AB,
∴DE∥CH,∴∠DEC=∠HCE.
∵∠B+∠A=90°,∠B+∠HCB=90°,
∴∠A=∠HCB.
∵AD=CD,∴∠A=∠ACD,
∴∠HCB=∠ACD.
∵CE平分∠ACB,∴∠ACE=∠BCE,
∴∠HCE=∠DCE,∴∠DEC=∠DCE,
∴CD=AD=DE.
在Rt△ACH 中, 在Rt△DCH 中,( 解得CD=2,
5.∵AB=3,AC=4,BC=5,3 +4 =5 ,
∴△ABC 是直角三角形,且∠A=90°,
∴在 Rt△ABP 中,
∵BP=CP,AP+CP=AC=4,AB=3,
6.(1)2 [解析]∵∠BAD=90°,AB=AD=2,
(2)如图,过点C作CE⊥AB交AB的延长线于点 E.
∵∠ABC=135°,
∴△BCE 是等腰直角三角形.
∴AE=AB+BE=3,
思路引导本题考查了勾股定理及等腰直角三角形的性质及判定,解决本题的关键是熟练掌握用勾股定理解决问题.(1)由勾股定理直接求出 BD 的长;
(2)过点C 作CE⊥AB交AB 的延长线于点E.先证明△BCE 是等腰直角三角形,再用勾股定理求出AC的长,最后求出 BD: AC.
7. B [解析]如图,连接BD.
∵∠A=90°,AD=AB=2,
∴∠ABD=∠ADB=45°,BD =8.
∴△BCD 是直角三角形,∠DBC=90°,
∴∠ABC=∠ABD+∠DBC=45°+90°=135°,即∠ABC 的度数是135°.故选 B.
■方法诠释 本题考查勾股定理和勾股定理逆定理的应用,因为求解的是角的度数,先根据等腰直角三角形得到∠ABD 的度数,然后利用勾股定理逆定理判定△BCD 是直角三角形来确定∠DBC 的度数,所以根据勾股定理确定BD 值时,不需要开方求出BD的确定值,只需要知道BD 的平方值即可.
8.(1)∵△BPC 绕点 B 逆时针旋转60°得到△BP'A,∴∠P'BP=60°,BP=BP',PC=P'A,∠BPC=∠BP'A,∴△P'BP 为等边三角形,
又PC=3,PB=4,PA=5,
∴P'A=PC=3,P'P=BP=4.
∴△P'PA 为直角三角形,
(2)如图(1),将△BPC 绕点B逆时针旋转 60°得到△BP'A,则∠P'BP =60°,BP =BP',PC=P'A,∠BPC=∠BP'A,
∴△P'BP 为等边三角形,
P'P=BP.
又PC=3,PB=4,PA=5,
∴△P'PA 为直角三角形,
∴∠BPC=∠BP'A=∠PP'A-∠BP'P=90°-
(3)如图(2),将△BPC 绕点 B 逆时针旋转90°得到△BEA,连接PE,
则∠PBE = 90°, BP = BE, PC = EA, ∠BPC=∠BEA,
∴△EBP 为等腰直角三角形,
∴∠BEP=∠BPE=45°.
又PC=3,∴EA=PC=3,
∴△EPA 为直角三角形,∠PEA=90°,
∴∠BPC=∠BEA =∠BEP +∠PEA =45°+
