19.3.4菱形的判定提优训练 (含答案)
文档属性
| 名称 | 19.3.4菱形的判定提优训练 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 184.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-15 12:52:02 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
19.3.4菱形的判定
1. 如图,□ABCD的对角线交于点O,添加下列条件不能判断四边形 ABCD 是菱形的是( ).
A. ∠BAC=∠DAC
B. ∠ABD=∠CBD
C. △AOB≌△BOC
D. △ABD≌△CDB
2.(2024·云南昭通期末)下面是关于如图的不完整推理过程:
∵∠BAD+∠ABC=180°,
∴AD∥BC.
∵AD=BC,
∴四边形 ABCD 是平行四边形.
∵ ,
∴四边形 ABCD 是菱形.
为使推理成立,横线上可以添加的条件是( ).
A. ∠BCD+∠ADC=180°
B. AC=BD
C.∠BAD+∠BCD=180°
D. AD=AB
3.如图,以矩形 ABCD 的顶点 A为圆心,AD 长为半径画弧交CB 的延长线于点E;过点 D 作DF∥AE 交BC 于点F,连接AF. AB=4,AD=5,则AF 的长是( ).
A. 2 B. 3 C. 3
4.如图,平行四边形 ABCD 的对角线AC,BD 相交于点 O,请你添加一个条件: ,使四边形 ABCD 是菱形.
5. 如图,已知四边形 ABCD 是平行四边形,其对角线相交于点O,OA=3,BD=8,AB=5.
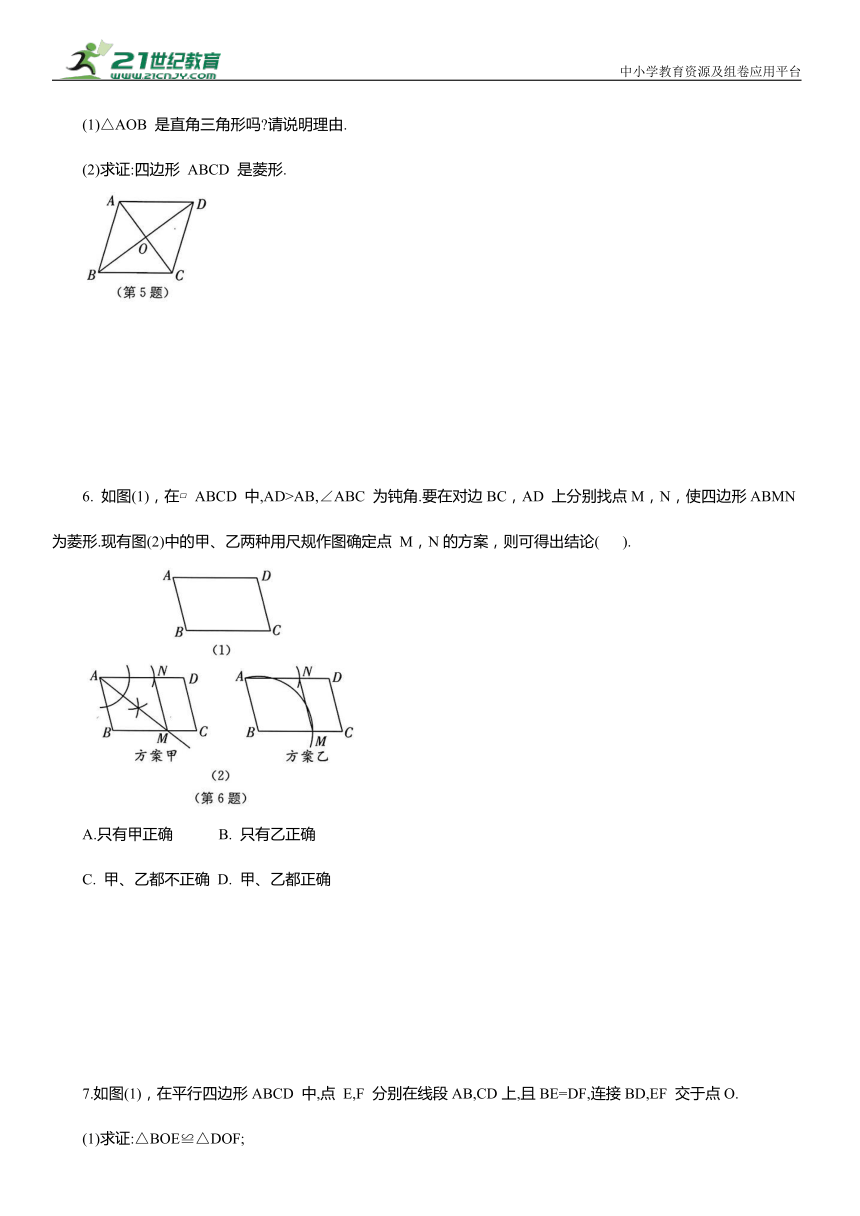
(1)△AOB 是直角三角形吗 请说明理由.
(2)求证:四边形 ABCD 是菱形.
6. 如图(1),在 ABCD 中,AD>AB,∠ABC 为钝角.要在对边BC,AD 上分别找点M,N,使四边形ABMN 为菱形.现有图(2)中的甲、乙两种用尺规作图确定点 M,N的方案,则可得出结论( ).
A.只有甲正确 B. 只有乙正确
C. 甲、乙都不正确 D. 甲、乙都正确
7.如图(1),在平行四边形ABCD 中,点 E,F 分别在线段AB,CD上,且BE=DF,连接BD,EF 交于点O.
(1)求证:△BOE≌△DOF;
(2)连接 BF,DE(如图(2)),若 BF=DF,求证:四边形 BFDE 是菱形.
8.如图,在 ABCD中,AE 是边BC 上的高,将△ABE 沿BC 方向平移,使点 E 与点C 重合,得到△GFC.
(1)求证:BE=DG.
(2)若∠B=60°,当AB 与 BC 满足什么数量关系时,四边形ABFG 是菱形 证明你的结论.
9.在平行四边形ABCD 中,对角线AC,BD 相交于点O,直线l经过点O,且与AB,CD 分别相交于点E,F,连接AF,CE.
(1)求证:四边形AECF 是平行四边形;
(2)若∠AEF=∠CEF,求证:四边形AECF是菱形.
10.如图,在 Rt△ABC 中,∠ACB=90°,D 是AB 的中点,连接CD,过点 B 作 BE∥CD,过点 C 作CE∥AB,BE,CE 相交于点E.
(1)求证:四边形CEBD 是菱形;
(2)过点 D 作DF⊥CE 于点 F,交CB 于点G,若AB=10,CF=3,求DG的长.
11.如图,在四边形ABCD 中,AC=a,BD=b,且AC⊥BD,顺次连接四边形ABCD 各边中点,得到四边形 A B C D ,再 顺 次 连 接 四 边 形A B C D 各边中点,得到四边形 A B C D ……如此进行下去,得到四边形AnBnCnDn.下列结论正确的是( ).
①四边形A B C D 是菱形;②四边形A B C D 是矩形;③四边形 A B C D 的周长为 ④四边形AnBnCnDn的面积为
A. ①②③ B. ②③④
C. ①③④ D. ①②③④
12.如图,在矩形ABCD 中,对角线AC,BD 相交于点O,P是线段AD 上一动点(不与点 D重合),PO的延长线交BC 于点Q.
(1)求证:四边形 PBQD 为平行四边形.
(2)若AB=6cm,AD=8cm,P从点A 出发,以1cm/s的速度向点 D 匀速运动.设点 P 运动时间为t s,问四边形 PBQD 能够成为菱形吗 如果能,求出相应的t值;如果不能,说明理由.
13.(2023·怀化中考)如图,在矩形ABCD 中,过对角线BD的中点O作BD 的垂线EF,分别交AD,BC于点E,F.
(1)求证:△BOF≌△DOE.
(2)连接BE,DF,求证:四边形EBFD 是菱形.
14.如图(1),将两个宽度相等的矩形纸条叠放在一起,得到四边形ABCD.
(1)试判断四边形 ABCD 的形状,并说明理由;
(2)已知矩形纸条宽度为2cm,将矩形纸条旋转至如图(2)位置时,四边形 ABCD 的面积为8cm ,求此时直线 AD,CD 所夹锐角∠1的度数.
第4课时 菱形的判定
1. D
2. D [解析]选项D的条件可以根据一组邻边相等的平行四边形是菱形判断.故选 D.
3. A [解析]∵四边形 ABCD 是矩形,AB=4,AD=5,∴AD∥BC,∠ABC=90°,∴∠ABE=90°.
∵DF∥AE,AD∥EF,
∴四边形 ADFE 是平行四边形.
由作图,得AE=AD=5.
∴四边形ADFE 是菱形,∴FE=AE=5.
∴BF=FE--BE=5-3=2,
故选 A.
4. AC⊥BD(答案不唯一)
5.(1)△AOB 是直角三角形.理由如下:
∵四边形ABCD 是平行四边形,BD=8,
∵OA=3,OB=4,AB=5,∴OA +OB =AB ,
∴△AOB 是直角三角形,且∠AOB=90°.
(2)由(1)可知,∠AOB=90°,
∴AC⊥BD,∴平行四边形ABCD 是菱形.
6. D [解析]方案甲:根据作图可知,AM平分∠DAB,AN=AB,∴∠NAM=∠BAM.
在 ABCD中,AD∥CB,
∴∠NAM=∠AMB,∴∠BAM=∠AMB,
∴AB=BM,∴AN=BM,
∴四边形ABMN 是平行四边形.
∵AB=AN,
∴四边形 ABMN 是菱形,故方案甲正确.
方案乙:根据作图可知BA=BM,AN=AB,则AN=BM.
∵AN∥BM,∴四边形ABMN 是平行四边形,
∵AB=AN,∴四边形ABMN 是菱形,故方案乙正确.故选 D.
7.(1)∵四边形 ABCD 是平行四边形,
∴AB∥CD,∴∠OBE=∠ODF.
在△BOE 和△DOF 中
∴△BOE≌△DOF(AAS).
(2)∵四边形ABCD 是平行四边形,∴BE∥DF,
∵BE=DF,∴四边形BFDE 是平行四边形,
∵BF=DF,∴平行四边形BFDE 是菱形.
■解后反思 本题考查了菱形的判定、平行四边形的性质以及全等三角形的判定等知识,熟练掌握以上知识是解题的关键.
8.(1)∵四边形ABCD 是平行四边形,∴AB=CD.
∵AE 是边BC 上的高,且 CG 是由AE 沿BC 方向平移而成,∴CG⊥AD.∴∠AEB=∠CGD=90°.
∵AE=CG,∴Rt△ABE≌Rt△CDG.∴BE=DG.
(2)当 时,四边形 ABFG 是菱形.证明如下:
∵AB∥GF,AG∥BF,∴四边形ABFG 是平行四边形.
在Rt△ABE 中,∵∠B=60°,
∴AB=BF.∴四边形ABFG 是菱形.
9.(1)∵四边形ABCD 是平行四边形,
∴AO=CO,AB∥CD,∴∠EAO=∠FCO.
在△AOE与△COF 中,
∴△AOE≌△COF(ASA),∴OE=OF.
∵AO=CO,∴四边形AECF 是平行四边形.
(2)∵AB∥CD,∴∠AEO=∠CFO.
∵∠AEF=∠CEF,∴∠CFO=∠CEF,
∴CE=CF.
由(1)知,四边形AECF 是平行四边形,∴四边形 AECF 是菱形.
10.(1)∵BE∥CD,CE∥AB,
∴四边形CEBD 是平行四边形.
在Rt△ABC 中,∠ACB=90°,D 是AB 的中点,
∴四边形CEBD 是菱形.
∵DF⊥CE,∴∠DFC=90°.
∵四边形CEBD 是菱形,
∴CE=CD=5,∠DCG=∠ECG,
∴EF=CE-CF=2,
在△DCG与△ECG中,
∴△DCG≌△ECG(SAS),∴DG=GE.
故 DG 的长为
■解后反思 本题考查了菱形的判定和性质、全等三角形的判定和性质、勾股定理、熟练掌握菱形的判定和性质定理是解题的关键.
11. A [解析]∵A ,B ,C ,D 分别为四边形 ABCD的各边中点,∴A D ∥BD,B C ∥BD,C D ∥AC,
∴四边形A B C D 是平行四边形.
∵AC⊥BD,∴A D ⊥A B ,
∴四边形A B C D 是矩形.
同理,得连接矩形A B C D 各边中点得到的四边形A B C D 是菱形,而连接菱形A B C D 各边中点得到的四边形A B C D 是矩形.
故四边形A B C D 是矩形,A B C D 是菱形.∴①②正确.
由三角形中位线性质易得,
∴四边形 A B C D 的周长为 ∴③正确.
∵在四边形 ABCD 中,AC=a,BD=b,且 AC⊥BD,∴S四边形ABCD=ab÷2.
由三角形中位线的性质可推知,每得到一次四边形,它的面积变为原来的一半,
∴四边形A B C D 的面积是 ∴④错误.
综上所述,结论正确的是①②③.故选 A.
关键提醒 本题以矩形的判定与性质、菱形的判定与性质为背景设置问题,考查规律总结知识.先根据四边形ABCD 的对角线垂直,结合三角形中位线判定四边形A B C D 是矩形,再由矩形的各边中点连线的四边形是菱形,菱形的各边中点连线的四边形是矩形,得到序号是奇数的四边形是矩形,序号是偶数的四边形是菱形,最后由三角形中位线性质得到每变化一次,面积变为原来的一半.据此逐项判断即可解答.
12.(1)∵四边形ABCD 是矩形,∴AD∥BC.
∴∠PDO=∠QBO.
在△POD 和△QOB 中
∴△POD≌△QOB(ASA).∴OP=OQ.
∵OB=OD,∴四边形PBQD 为平行四边形.
(2)四边形 PBQD 能成为菱形.理由如下:
由题意,得AP=t,PD=8-t,
若四边形PBQD 是菱形,则PD=BP=8-t.
∵四边形ABCD 是矩形,∴∠A=90°.
在 Rt△ABP 中,由勾股定理,得. 即 解得
故当点 P 运动时间为 s时,四边形 PBQD 是菱形.
■素养考向 本题运用平行四边形的判定、矩形的性质以及菱形的判定与性质.经过推理与计算,使问题得以解决.考查了推理能力和运算能力的核心素养.
13.(1)∵四边形ABCD 是矩形,
∴AD∥BC,∴∠EDO=∠FBO.
∵O是BD的中点,∴DO=BO.
∵∠EOD=∠FOB,
∴△BOF≌△DOE.
(2)由(1)知,△BOF≌△DOE,∴BF=DE.
∵四边形ABCD 是矩形,
∴AD∥BC,即DE∥BF,
∴四边形EBFD 是平行四边形.
∵EF⊥BD,∴四边形EBFD 是菱形.
14.(1)四边形ABCD 是菱形.理由如下:
如图(1),过点C作CH⊥AB,垂足为 H,作 CG⊥AD,垂足为G.
∵两个纸条为宽度相等的矩形,
∴AB∥CD,AD∥BC,CH=CG,
∴四边形ABCD 是平行四边形.
∵S□ABCD=AB·CH=AD·CG,且CH=CG,
∴AB=AD,∴平行四边形 ABCD 是菱形.
(2)如图(2),作AM⊥CD,垂足为M,
∵S菱形ABCD=CD·AM=8cm ,且AM=2cm,
∴CD=4cm,
∴AD=CD=4 cm.在Rt△ADM中,AD=2AM,
∴∠1=30°.
19.3.4菱形的判定
1. 如图,□ABCD的对角线交于点O,添加下列条件不能判断四边形 ABCD 是菱形的是( ).
A. ∠BAC=∠DAC
B. ∠ABD=∠CBD
C. △AOB≌△BOC
D. △ABD≌△CDB
2.(2024·云南昭通期末)下面是关于如图的不完整推理过程:
∵∠BAD+∠ABC=180°,
∴AD∥BC.
∵AD=BC,
∴四边形 ABCD 是平行四边形.
∵ ,
∴四边形 ABCD 是菱形.
为使推理成立,横线上可以添加的条件是( ).
A. ∠BCD+∠ADC=180°
B. AC=BD
C.∠BAD+∠BCD=180°
D. AD=AB
3.如图,以矩形 ABCD 的顶点 A为圆心,AD 长为半径画弧交CB 的延长线于点E;过点 D 作DF∥AE 交BC 于点F,连接AF. AB=4,AD=5,则AF 的长是( ).
A. 2 B. 3 C. 3
4.如图,平行四边形 ABCD 的对角线AC,BD 相交于点 O,请你添加一个条件: ,使四边形 ABCD 是菱形.
5. 如图,已知四边形 ABCD 是平行四边形,其对角线相交于点O,OA=3,BD=8,AB=5.
(1)△AOB 是直角三角形吗 请说明理由.
(2)求证:四边形 ABCD 是菱形.
6. 如图(1),在 ABCD 中,AD>AB,∠ABC 为钝角.要在对边BC,AD 上分别找点M,N,使四边形ABMN 为菱形.现有图(2)中的甲、乙两种用尺规作图确定点 M,N的方案,则可得出结论( ).
A.只有甲正确 B. 只有乙正确
C. 甲、乙都不正确 D. 甲、乙都正确
7.如图(1),在平行四边形ABCD 中,点 E,F 分别在线段AB,CD上,且BE=DF,连接BD,EF 交于点O.
(1)求证:△BOE≌△DOF;
(2)连接 BF,DE(如图(2)),若 BF=DF,求证:四边形 BFDE 是菱形.
8.如图,在 ABCD中,AE 是边BC 上的高,将△ABE 沿BC 方向平移,使点 E 与点C 重合,得到△GFC.
(1)求证:BE=DG.
(2)若∠B=60°,当AB 与 BC 满足什么数量关系时,四边形ABFG 是菱形 证明你的结论.
9.在平行四边形ABCD 中,对角线AC,BD 相交于点O,直线l经过点O,且与AB,CD 分别相交于点E,F,连接AF,CE.
(1)求证:四边形AECF 是平行四边形;
(2)若∠AEF=∠CEF,求证:四边形AECF是菱形.
10.如图,在 Rt△ABC 中,∠ACB=90°,D 是AB 的中点,连接CD,过点 B 作 BE∥CD,过点 C 作CE∥AB,BE,CE 相交于点E.
(1)求证:四边形CEBD 是菱形;
(2)过点 D 作DF⊥CE 于点 F,交CB 于点G,若AB=10,CF=3,求DG的长.
11.如图,在四边形ABCD 中,AC=a,BD=b,且AC⊥BD,顺次连接四边形ABCD 各边中点,得到四边形 A B C D ,再 顺 次 连 接 四 边 形A B C D 各边中点,得到四边形 A B C D ……如此进行下去,得到四边形AnBnCnDn.下列结论正确的是( ).
①四边形A B C D 是菱形;②四边形A B C D 是矩形;③四边形 A B C D 的周长为 ④四边形AnBnCnDn的面积为
A. ①②③ B. ②③④
C. ①③④ D. ①②③④
12.如图,在矩形ABCD 中,对角线AC,BD 相交于点O,P是线段AD 上一动点(不与点 D重合),PO的延长线交BC 于点Q.
(1)求证:四边形 PBQD 为平行四边形.
(2)若AB=6cm,AD=8cm,P从点A 出发,以1cm/s的速度向点 D 匀速运动.设点 P 运动时间为t s,问四边形 PBQD 能够成为菱形吗 如果能,求出相应的t值;如果不能,说明理由.
13.(2023·怀化中考)如图,在矩形ABCD 中,过对角线BD的中点O作BD 的垂线EF,分别交AD,BC于点E,F.
(1)求证:△BOF≌△DOE.
(2)连接BE,DF,求证:四边形EBFD 是菱形.
14.如图(1),将两个宽度相等的矩形纸条叠放在一起,得到四边形ABCD.
(1)试判断四边形 ABCD 的形状,并说明理由;
(2)已知矩形纸条宽度为2cm,将矩形纸条旋转至如图(2)位置时,四边形 ABCD 的面积为8cm ,求此时直线 AD,CD 所夹锐角∠1的度数.
第4课时 菱形的判定
1. D
2. D [解析]选项D的条件可以根据一组邻边相等的平行四边形是菱形判断.故选 D.
3. A [解析]∵四边形 ABCD 是矩形,AB=4,AD=5,∴AD∥BC,∠ABC=90°,∴∠ABE=90°.
∵DF∥AE,AD∥EF,
∴四边形 ADFE 是平行四边形.
由作图,得AE=AD=5.
∴四边形ADFE 是菱形,∴FE=AE=5.
∴BF=FE--BE=5-3=2,
故选 A.
4. AC⊥BD(答案不唯一)
5.(1)△AOB 是直角三角形.理由如下:
∵四边形ABCD 是平行四边形,BD=8,
∵OA=3,OB=4,AB=5,∴OA +OB =AB ,
∴△AOB 是直角三角形,且∠AOB=90°.
(2)由(1)可知,∠AOB=90°,
∴AC⊥BD,∴平行四边形ABCD 是菱形.
6. D [解析]方案甲:根据作图可知,AM平分∠DAB,AN=AB,∴∠NAM=∠BAM.
在 ABCD中,AD∥CB,
∴∠NAM=∠AMB,∴∠BAM=∠AMB,
∴AB=BM,∴AN=BM,
∴四边形ABMN 是平行四边形.
∵AB=AN,
∴四边形 ABMN 是菱形,故方案甲正确.
方案乙:根据作图可知BA=BM,AN=AB,则AN=BM.
∵AN∥BM,∴四边形ABMN 是平行四边形,
∵AB=AN,∴四边形ABMN 是菱形,故方案乙正确.故选 D.
7.(1)∵四边形 ABCD 是平行四边形,
∴AB∥CD,∴∠OBE=∠ODF.
在△BOE 和△DOF 中
∴△BOE≌△DOF(AAS).
(2)∵四边形ABCD 是平行四边形,∴BE∥DF,
∵BE=DF,∴四边形BFDE 是平行四边形,
∵BF=DF,∴平行四边形BFDE 是菱形.
■解后反思 本题考查了菱形的判定、平行四边形的性质以及全等三角形的判定等知识,熟练掌握以上知识是解题的关键.
8.(1)∵四边形ABCD 是平行四边形,∴AB=CD.
∵AE 是边BC 上的高,且 CG 是由AE 沿BC 方向平移而成,∴CG⊥AD.∴∠AEB=∠CGD=90°.
∵AE=CG,∴Rt△ABE≌Rt△CDG.∴BE=DG.
(2)当 时,四边形 ABFG 是菱形.证明如下:
∵AB∥GF,AG∥BF,∴四边形ABFG 是平行四边形.
在Rt△ABE 中,∵∠B=60°,
∴AB=BF.∴四边形ABFG 是菱形.
9.(1)∵四边形ABCD 是平行四边形,
∴AO=CO,AB∥CD,∴∠EAO=∠FCO.
在△AOE与△COF 中,
∴△AOE≌△COF(ASA),∴OE=OF.
∵AO=CO,∴四边形AECF 是平行四边形.
(2)∵AB∥CD,∴∠AEO=∠CFO.
∵∠AEF=∠CEF,∴∠CFO=∠CEF,
∴CE=CF.
由(1)知,四边形AECF 是平行四边形,∴四边形 AECF 是菱形.
10.(1)∵BE∥CD,CE∥AB,
∴四边形CEBD 是平行四边形.
在Rt△ABC 中,∠ACB=90°,D 是AB 的中点,
∴四边形CEBD 是菱形.
∵DF⊥CE,∴∠DFC=90°.
∵四边形CEBD 是菱形,
∴CE=CD=5,∠DCG=∠ECG,
∴EF=CE-CF=2,
在△DCG与△ECG中,
∴△DCG≌△ECG(SAS),∴DG=GE.
故 DG 的长为
■解后反思 本题考查了菱形的判定和性质、全等三角形的判定和性质、勾股定理、熟练掌握菱形的判定和性质定理是解题的关键.
11. A [解析]∵A ,B ,C ,D 分别为四边形 ABCD的各边中点,∴A D ∥BD,B C ∥BD,C D ∥AC,
∴四边形A B C D 是平行四边形.
∵AC⊥BD,∴A D ⊥A B ,
∴四边形A B C D 是矩形.
同理,得连接矩形A B C D 各边中点得到的四边形A B C D 是菱形,而连接菱形A B C D 各边中点得到的四边形A B C D 是矩形.
故四边形A B C D 是矩形,A B C D 是菱形.∴①②正确.
由三角形中位线性质易得,
∴四边形 A B C D 的周长为 ∴③正确.
∵在四边形 ABCD 中,AC=a,BD=b,且 AC⊥BD,∴S四边形ABCD=ab÷2.
由三角形中位线的性质可推知,每得到一次四边形,它的面积变为原来的一半,
∴四边形A B C D 的面积是 ∴④错误.
综上所述,结论正确的是①②③.故选 A.
关键提醒 本题以矩形的判定与性质、菱形的判定与性质为背景设置问题,考查规律总结知识.先根据四边形ABCD 的对角线垂直,结合三角形中位线判定四边形A B C D 是矩形,再由矩形的各边中点连线的四边形是菱形,菱形的各边中点连线的四边形是矩形,得到序号是奇数的四边形是矩形,序号是偶数的四边形是菱形,最后由三角形中位线性质得到每变化一次,面积变为原来的一半.据此逐项判断即可解答.
12.(1)∵四边形ABCD 是矩形,∴AD∥BC.
∴∠PDO=∠QBO.
在△POD 和△QOB 中
∴△POD≌△QOB(ASA).∴OP=OQ.
∵OB=OD,∴四边形PBQD 为平行四边形.
(2)四边形 PBQD 能成为菱形.理由如下:
由题意,得AP=t,PD=8-t,
若四边形PBQD 是菱形,则PD=BP=8-t.
∵四边形ABCD 是矩形,∴∠A=90°.
在 Rt△ABP 中,由勾股定理,得. 即 解得
故当点 P 运动时间为 s时,四边形 PBQD 是菱形.
■素养考向 本题运用平行四边形的判定、矩形的性质以及菱形的判定与性质.经过推理与计算,使问题得以解决.考查了推理能力和运算能力的核心素养.
13.(1)∵四边形ABCD 是矩形,
∴AD∥BC,∴∠EDO=∠FBO.
∵O是BD的中点,∴DO=BO.
∵∠EOD=∠FOB,
∴△BOF≌△DOE.
(2)由(1)知,△BOF≌△DOE,∴BF=DE.
∵四边形ABCD 是矩形,
∴AD∥BC,即DE∥BF,
∴四边形EBFD 是平行四边形.
∵EF⊥BD,∴四边形EBFD 是菱形.
14.(1)四边形ABCD 是菱形.理由如下:
如图(1),过点C作CH⊥AB,垂足为 H,作 CG⊥AD,垂足为G.
∵两个纸条为宽度相等的矩形,
∴AB∥CD,AD∥BC,CH=CG,
∴四边形ABCD 是平行四边形.
∵S□ABCD=AB·CH=AD·CG,且CH=CG,
∴AB=AD,∴平行四边形 ABCD 是菱形.
(2)如图(2),作AM⊥CD,垂足为M,
∵S菱形ABCD=CD·AM=8cm ,且AM=2cm,
∴CD=4cm,
∴AD=CD=4 cm.在Rt△ADM中,AD=2AM,
∴∠1=30°.
