19.3.5正方形提优训练 (含答案)
文档属性
| 名称 | 19.3.5正方形提优训练 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 237.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-15 12:50:59 | ||
图片预览



文档简介
19.3.5正方形
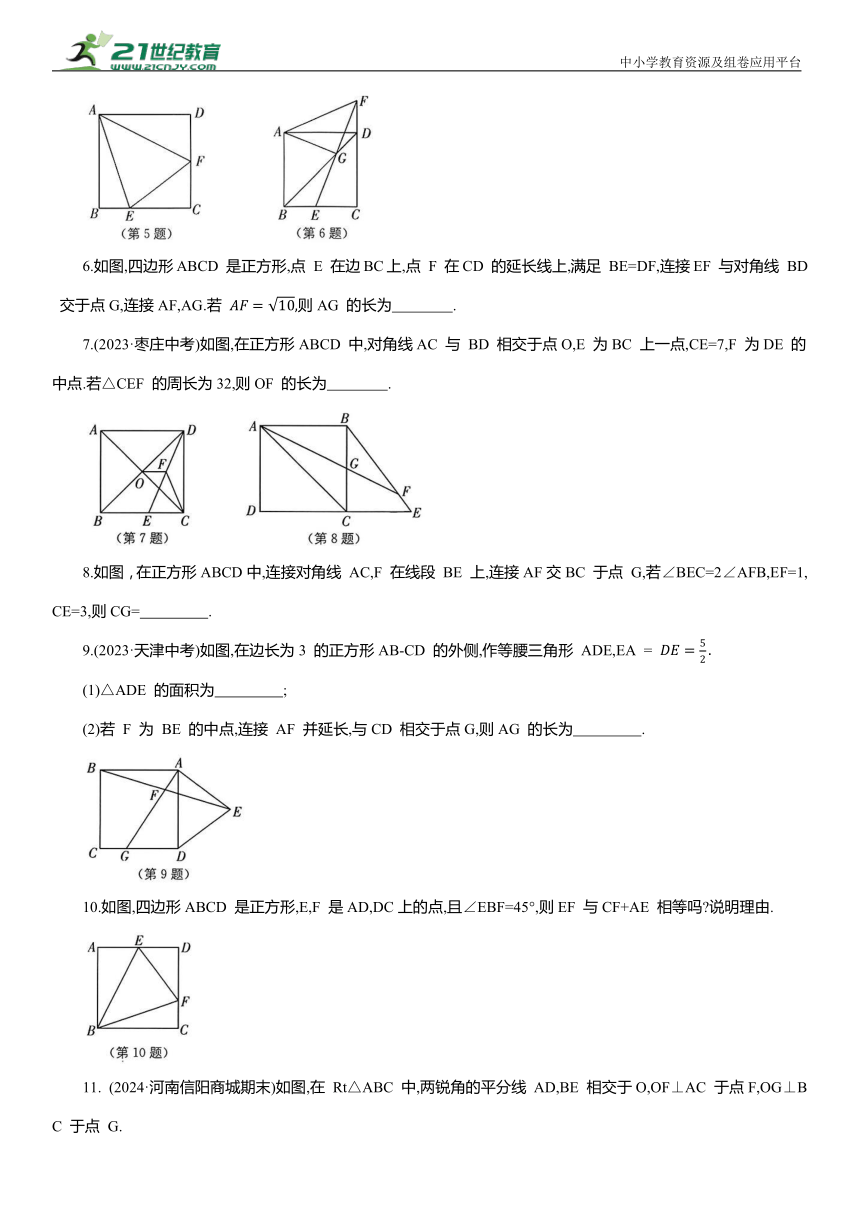
1. 下列说法不正确的是( ).
A.对角线相等的平行四边形是矩形
B.邻边相等的平行四边形是菱形
C.对角线互相垂直平分的四边形是正方形
D.三个角为直角且邻边相等的四边形是正方形
2.如图(1),小言用七巧板拼了一个对角线长为6的正方形,再用这副七巧板拼成一个矩形(如图(2)所示),则矩形的对角线长为 .
3.如图,等边三角形 AEF 的顶点E,F 在矩形ABCD 的边BC,CD 上,且∠CEF=45°.求证:矩形ABCD 是正方形.
4.如图,在正方形ABCD中,AE∥BD,BE=BD,BE 交AD 于点F.求证:DE=DF.
5.如图,在正方形 ABCD 中,点E,F分别在BC,CD上,连接AE,AF,EF,∠EAF=45°.若∠BAE=α,则∠FEC一定等于( ).
A. 2α
C. 45°-α
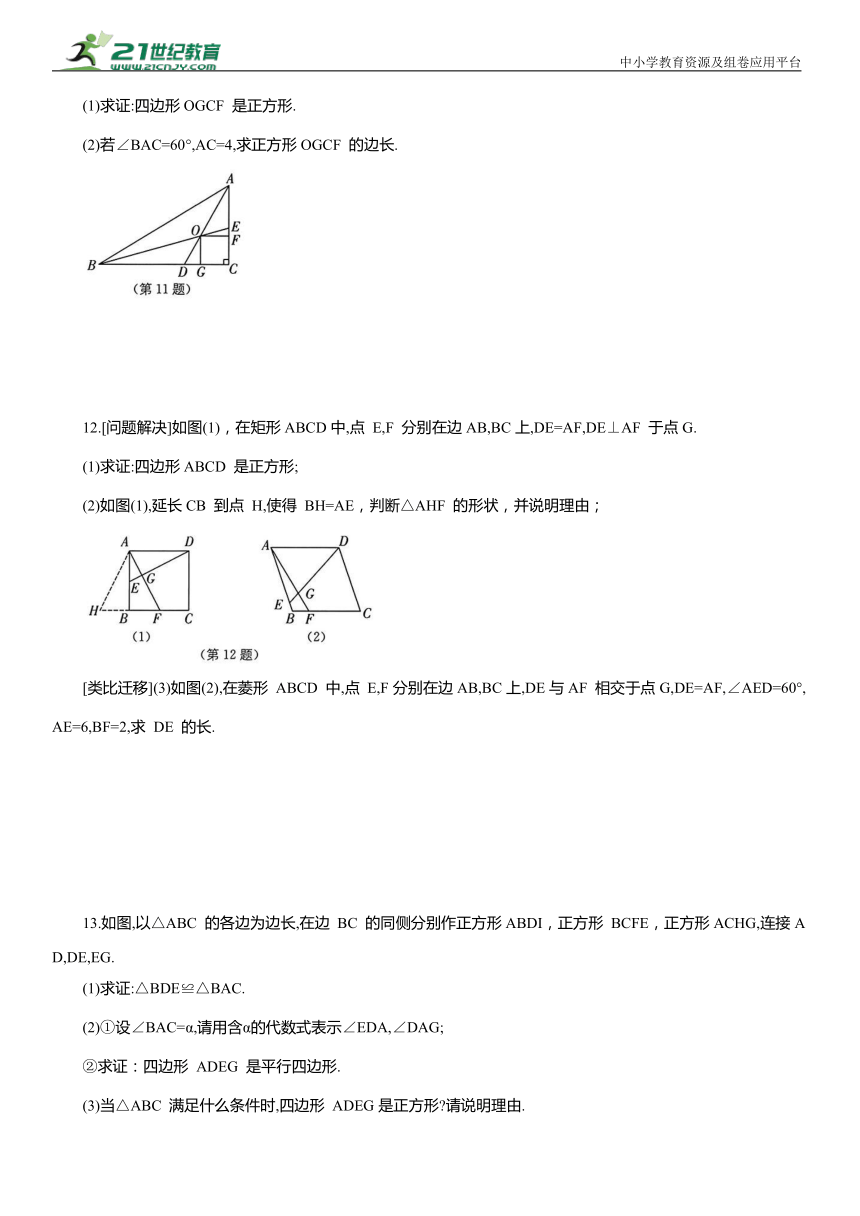
6.如图,四边形ABCD 是正方形,点 E 在边BC上,点 F 在CD 的延长线上,满足 BE=DF,连接EF 与对角线 BD 交于点G,连接AF,AG.若 则AG 的长为 .
7.(2023·枣庄中考)如图,在正方形ABCD 中,对角线AC 与 BD 相交于点O,E 为BC 上一点,CE=7,F 为DE 的中点.若△CEF 的周长为32,则OF 的长为 .
8.如图,在正方形ABCD中,连接对角线 AC,F 在线段 BE 上,连接AF交BC 于点 G,若∠BEC=2∠AFB,EF=1,CE=3,则CG= .
9.(2023·天津中考)如图,在边长为3 的正方形AB-CD 的外侧,作等腰三角形 ADE,EA =
(1)△ADE 的面积为 ;
(2)若 F 为 BE 的中点,连接 AF 并延长,与CD 相交于点G,则AG 的长为 .
10.如图,四边形ABCD 是正方形,E,F 是AD,DC上的点,且∠EBF=45°,则EF 与CF+AE 相等吗 说明理由.
11. (2024·河南信阳商城期末)如图,在 Rt△ABC 中,两锐角的平分线 AD,BE 相交于O,OF⊥AC 于点F,OG⊥BC 于点 G.
(1)求证:四边形OGCF 是正方形.
(2)若∠BAC=60°,AC=4,求正方形OGCF 的边长.
12.[问题解决]如图(1),在矩形ABCD中,点 E,F 分别在边AB,BC上,DE=AF,DE⊥AF 于点G.
(1)求证:四边形ABCD 是正方形;
(2)如图(1),延长CB 到点 H,使得 BH=AE,判断△AHF 的形状,并说明理由;
[类比迁移](3)如图(2),在菱形 ABCD 中,点 E,F分别在边AB,BC上,DE与AF 相交于点G,DE=AF,∠AED=60°,AE=6,BF=2,求 DE 的长.
13.如图,以△ABC 的各边为边长,在边 BC 的同侧分别作正方形ABDI,正方形 BCFE,正方形ACHG,连接AD,DE,EG.
(1)求证:△BDE≌△BAC.
(2)①设∠BAC=α,请用含α的代数式表示∠EDA,∠DAG;
②求证:四边形 ADEG 是平行四边形.
(3)当△ABC 满足什么条件时,四边形 ADEG是正方形 请说明理由.
14.(2024·天津中考)如图,正方形ABCD的边长为3 对角线 AC,BD 相交于点O,点 E 在 CA 的延长线上,OE=5,连接DE.
(1)线段AE 的长为 ;
(2)若 F 为 DE 的中点,则线段 AF 的长为
15.如图,□ABCD的对角线AC,BD 交于点O,分别以点B,C为圆心, AC, BD 长为半径画弧,两弧交于点 P,连接BP,CP.
(1)试判断四边形 BPCO 的形状,并说明理由.
(2)请说明当□ABCD 的对角线满足什么条件时,四边形 BPCO 是正方形
中小学教育资源及组卷应用平台
1. C [解析]对角线互相垂直平分的四边形是菱形,而不是正方形,故C选项符合题意.故选 C.
2.3 [解析]∵正方形对角线为6,∴①和②的直角边为3,∴矩形的长为6,宽为3,∴矩形的对角线长为
3.∵四边形ABCD是矩形,∴∠B=∠D=∠C=90°.
∵△AEF 是等边三角形,
∴AE=AF,∠AEF=∠AFE=60°.
∵∠CEF=45°,∴∠CFE=∠CEF=45°.
∴△AEB≌△AFD.∴AB=AD.
∴矩形ABCD 是正方形.
4.如图,连接AC交BD 于点O,过点 E 作EG⊥BD 于点G.
∵四边形 ABCD 是正方形,
∴∠AOG=90°.∵AE∥BD,
∴∠EAO=90°.又∠DGE=90°,
∴四边形 AOGE 是矩形.
∴∠EBD=30°.又BE=BD,
∵∠EFD=∠FDB+∠EBD=45°+30°=75°,
∴∠DEF=∠DFE.∴DF=DE.
5. A [解析]在正方形ABCD中,AD=AB,∠BAD=∠ABC=∠ADC=90°.
如图,将△ADF 绕点A 顺时针旋转90°,得△ABG,则AF=AG,∠DAF=∠BAG.
∵∠EAF=45°,∴∠BAE+∠DAF=45°,
∴∠GAE=∠FAE=45°.
在△FAE 和△GAE 中,
∴△FAE≌△GAE(SAS),∴∠AEF=∠AEG.
∵∠BAE=α,∴∠AEB=90°-α,
∴∠AEF=∠AEB=90°-α,
故选 A.
知识拓展 正方形的性质:1.四边相等且邻边相互垂直;2.对角线互相垂直平分且相等;3.每条对角线平分一组对角;4.每条对角线将正方形分为两个相等的等腰直角三角形;5.正方形既是轴对称图形,又是中心对称图形;6.正方形是邻边相等的特殊的矩形,是内角为直角的特殊的菱形.
6. [解析]如图,连接AE.
∵四边形ABCD 是正方形,
∴AB=AD,∠ABE=∠ADC=90°=∠ADF.
在△ABE 和△ADF 中,
∴△ABE≌△ADF(SAS),
∴AE=AF,∠DAF=∠BAE.
∵∠BAE+∠DAE=90°,
∴∠DAF+∠DAE=90°,
∴△EAF 是等腰直角三角形,∴∠AFG=45°.过点E作EH⊥BC交BD 于点 H.
∵∠DBC=45°,∠BEH=90°,
∴△BEH 是等腰直角三角形,
∴HE=BE=DF.
∵EH⊥BC,∴EH∥CD,
∴∠GHE=∠GDF,∠GEH=∠GFD,
∴△GHE≌△GDF,
∴EG=FG.
∵AE=AF,∴AG⊥FG,
∴△AGF 是等腰直角三角形.
7. [解析]在正方形 ABCD 中,对角线 AC 与 BD相交于点O,∴∠BCD=90°,O是BD的中点.
∵F为DE的中点,∴CF=EF=DF.
∵△CEF 的周长为32,CE=7,
∴CF+EF=25,即DE=25.
在 Rt△CDE中,根据勾股定理,得 ∴BE=24-7=17.
根据三角形的中位线定理,得
8.2 [解析]延长AF,DE 交于点 H,如图所示.
由图,得∠AFB=∠HFE.
∵∠BEC=2∠AFB,∴∠BEC=2∠HFE.
∵∠BEC=∠HFE+∠FHE,
∴∠HFE=∠FHE=∠AFB.
∵EF=1,∴EH=EF=1.
∵CE=3,∴CH=CE+EH=3+1=4.
∵四边形ABCD 为正方形,∴AB∥DH,
∴∠BAH=∠FHE,即∠BAH=∠AFB,
∴AB=BF.
设正方形ABCD边长为x,
则BC=x,AB=BF=x,BE=BF+FE=x+1.
∵△BCE 为直角三角形, 即 解得x=4.
在△ABG 和△HCG 中,
∴△ABG≌△HCG(ASA),∴CG=BG=2.
思路引导本题考查了正方形的性质、勾股定理、全等三角形的判定及性质、等腰三角形的判定,以利用条件“∠BEC=2∠AFB”和“AB∥DE”为突破口,想到添加辅助线“延长AF,DE 交于一点 H”是解题的关键.
9.(1)3 [解析]如图,过E 作EM⊥AD 于点M.
∴△ADE 的面积为
[解析]如图,过E 作 AD的垂线分别交AD,AG,BC于点M,N,P.
∵四边形ABCD 是正方形,∴BC∥AD,
∴EP⊥BC,∴四边形ABPM是矩形,
∴PM=AB=3,AB∥EP,
∴∠ABF=∠NEF.
∵F为BE 的中点,∴BF=EF.
在△ABF 与△NEF 中
∴△ABF≌△NEF(ASA),
∴EN=AB=3.
∴在 Rt△AEM中,
∴MN=1.
∵PM∥CD,∴AN=NG,
∴GD=2MN=2,
10. EF=CF+AE.理由如下:
延长FC到点P,使CP=AE,连接BP.
∵四边形ABCD 是正方形,
∴AB=BC,∠A=∠BCD=∠BCP=90°.
∵AE=CP,∴△ABE≌△CBP.
∴BE=BP,∠ABE=∠CBP.
∵∠ABC=∠ABE+∠EBC=90°,
∴∠CBP+∠EBC=90°,即∠EBP=90°.
∵∠EBF=45°,∴∠PBF=∠EBP-∠EBF=45°.
∴∠EBF=∠PBF=45°.
∵BE=BP,BF=BF,
∴△EBF≌△PBF.∴EF=PF.
∵PF=PC+CF,CP=AE,∴EF=CF+AE.
11.(1)如图,过点O作OH⊥AB 于点 H.
∵OF⊥AC于点F,OG⊥BC 于点G,
∴∠OGC=∠OFC=90°.
∴四边形OGCF 是矩形.
∵AD,BE 分别是∠BAC,∠ABC 的平分线,OF⊥AC,OG⊥BC,OH⊥AB,
∴OG=OH=OF.
又四边形OGCF 是矩形,
∴矩形 OGCF 是正方形.
(2)在 Rt△ABC 中,∵∠BAC=60°,
∴AB=2AC=2×4=8.
在 Rt△AOH 和 Rt△AOF 中,
∴Rt△AOH≌Rt△AOF(HL),
∴AH=AF,
设正方形OGCF 的边长为x,
则AH=AF=4-x,BH=BG=4 -x,
即正方形OGCF 的边长为
12.(1)∵四边形ABCD 是矩形,
∴∠DAB=∠ABC=90°.
∵DE⊥AF,∴∠DAB=∠AGD=90°.
∴∠BAF+∠DAF=90°,∠ADE+∠DAF=90°.
∴∠ADE=∠BAF.
∵DE=AF,∴△ADE≌△BAF.∴AD=AB.
∵四边形 ABCD 是矩形,
∴矩形 ABCD 是正方形.
(2)△AHF 是等腰三角形.理由如下:
∵四边形 ABCD 是正方形,
∴∠DAB=∠ABH=90°,AB=DA.
∵BH=AE,∴△DAE≌△ABH.∴AH=DE.
∵DE=AF,∴AH=AF.
∴△AHF是等腰三角形.
(3)如图,延长CB 到点 H,使BH=AE=6,连接AH.
∵四边形ABCD 是菱形,
∴AD∥BC,AB=AD.
∴∠ABH=∠BAD.
∵BH=AE,
∴△DAE≌△ABH.
∴AH=DE,∠H=∠AED=60°.
∵DE=AF,∴AH=AF.
∴△AHF 是等边三角形.
∴AH=HF=HB+BF=AE+BF=6+2=8.
∴DE=AH=8.
13.(1)∵四边形ABDI,四边形BCFE,四边形 ACHG都是正方形,
∴AC=AG,AB=BD,BC=BE,
∠GAC=∠EBC=∠DBA=90°.
∴∠ABC=∠EBD(同为∠EBA 的余角).
在△BDE 和△BAC中
∴△BDE≌△BAC(SAS).
(2)①∵△BDE≌△BAC,∠ADB=∠BAD=45°,∠BAC=α,∴∠EDA=α-45°,∠DAG=360°-45°-
②∵△BDE≌△BAC,
∴DE=AC=AG,∠BAC=∠BDE.
∵AD 是正方形ABDI 的对角线,
∴∠BDA=∠BAD=45°.
∵∠EDA=∠BDE-∠BDA=∠BDE-45°,由①,知∠DAG=225°-∠BAC.
180°.∴DE∥AG.
∴四边形ADEG 是平行四边形.
(3)当△ABC满足∠BAC=135°,且 时,四边形ADEG 是正方形.理由如下:
由①知,当∠BAC=135°时,∠DAG=90°.
∵四边形 ABDI 是正方形,
又四边形ACHG 是正方形,
∴当∠BAC=135°且. 时,四边形ADEG是正方形.
素养考向本题综合运用了正方形的判定与性质、全等三角形的判定与性质、平行四边形的性质、勾股定理等知识点.考查了推理能力和运算能力的核心素养.
14.(1)2 [解析]∵四边形ABCD 是正方形,∴OA=OC=OD=OB,∠DOC=90°,∴在 Rt△DOC 中, OC=OB=3.∵OE=5,∴AE=OE--OA=2.
[解析]如图,延长DA 到点G,使AG=AD,连接EG,过E作EH⊥AG 于点 H.
∵F 为DE 中点,A 为DG中点,∴AF 为△DGE 中位线,
在Rt△EAH 中,∠EAH=∠DAC=45°,∴AH=EH.
在 Rt△EGH 中,
难点突破 本题的难点是第(2)问,与线段AF有关的图形中的边、角的信息有AF 在△AED中,∠EAD= 点F 为DE的中点,AE=2,AD= 但直接利用这些信息都无法求出线段AF 的长,因此需要作出辅助线,“点F 为 DE 的中点”易联想到中位线定理,“∠EAD=135°”易联想到等腰直角三角形于是想到:延长 DA 到点G,使 AG=AD,连接EG,过点E 作EH⊥AG 于点 H.
15.(1)四边形 BPCO 为平行四边形.理由如下:
∵四边形ABCD 为平行四边形,
∵以点B,C为圆心, AC, BD长为半径画弧,两弧交于点 P,
∴OB=CP,BP=OC,
∴四边形 BPCO 为平行四边形.
(2)当AC⊥BD,AC=BD时,四边形BPCO 为正方形.
∵AC⊥BD,∴∠BOC=90°,
∵四边形 BPCO 为平行四边形,
∴平行四边形 BPCO 为正方形.
■知识拓展 本题考查了平行四边形的性质与判定、正方形的判定,熟练掌握以上知识是解题的关键.正方形的判定方法主要有:(1)对角线相等的菱形是正方形;(2)有一个角为直角的菱形是正方形;(3)对角线互相垂直的矩形是正方形;(4)一组邻边相等的矩形是正方形;(5)一组邻边相等且有一个角是直角的平行四边形是正方形;(6)对角线互相垂直且相等的平行四边形是正方形;(7)对角线相等且互相垂直平分的四边形是正方形;(8)一组邻边相等,有三个角是直角的四边形是正方形;(9)既是菱形又是矩形的四边形是正方形.
1. 下列说法不正确的是( ).
A.对角线相等的平行四边形是矩形
B.邻边相等的平行四边形是菱形
C.对角线互相垂直平分的四边形是正方形
D.三个角为直角且邻边相等的四边形是正方形
2.如图(1),小言用七巧板拼了一个对角线长为6的正方形,再用这副七巧板拼成一个矩形(如图(2)所示),则矩形的对角线长为 .
3.如图,等边三角形 AEF 的顶点E,F 在矩形ABCD 的边BC,CD 上,且∠CEF=45°.求证:矩形ABCD 是正方形.
4.如图,在正方形ABCD中,AE∥BD,BE=BD,BE 交AD 于点F.求证:DE=DF.
5.如图,在正方形 ABCD 中,点E,F分别在BC,CD上,连接AE,AF,EF,∠EAF=45°.若∠BAE=α,则∠FEC一定等于( ).
A. 2α
C. 45°-α
6.如图,四边形ABCD 是正方形,点 E 在边BC上,点 F 在CD 的延长线上,满足 BE=DF,连接EF 与对角线 BD 交于点G,连接AF,AG.若 则AG 的长为 .
7.(2023·枣庄中考)如图,在正方形ABCD 中,对角线AC 与 BD 相交于点O,E 为BC 上一点,CE=7,F 为DE 的中点.若△CEF 的周长为32,则OF 的长为 .
8.如图,在正方形ABCD中,连接对角线 AC,F 在线段 BE 上,连接AF交BC 于点 G,若∠BEC=2∠AFB,EF=1,CE=3,则CG= .
9.(2023·天津中考)如图,在边长为3 的正方形AB-CD 的外侧,作等腰三角形 ADE,EA =
(1)△ADE 的面积为 ;
(2)若 F 为 BE 的中点,连接 AF 并延长,与CD 相交于点G,则AG 的长为 .
10.如图,四边形ABCD 是正方形,E,F 是AD,DC上的点,且∠EBF=45°,则EF 与CF+AE 相等吗 说明理由.
11. (2024·河南信阳商城期末)如图,在 Rt△ABC 中,两锐角的平分线 AD,BE 相交于O,OF⊥AC 于点F,OG⊥BC 于点 G.
(1)求证:四边形OGCF 是正方形.
(2)若∠BAC=60°,AC=4,求正方形OGCF 的边长.
12.[问题解决]如图(1),在矩形ABCD中,点 E,F 分别在边AB,BC上,DE=AF,DE⊥AF 于点G.
(1)求证:四边形ABCD 是正方形;
(2)如图(1),延长CB 到点 H,使得 BH=AE,判断△AHF 的形状,并说明理由;
[类比迁移](3)如图(2),在菱形 ABCD 中,点 E,F分别在边AB,BC上,DE与AF 相交于点G,DE=AF,∠AED=60°,AE=6,BF=2,求 DE 的长.
13.如图,以△ABC 的各边为边长,在边 BC 的同侧分别作正方形ABDI,正方形 BCFE,正方形ACHG,连接AD,DE,EG.
(1)求证:△BDE≌△BAC.
(2)①设∠BAC=α,请用含α的代数式表示∠EDA,∠DAG;
②求证:四边形 ADEG 是平行四边形.
(3)当△ABC 满足什么条件时,四边形 ADEG是正方形 请说明理由.
14.(2024·天津中考)如图,正方形ABCD的边长为3 对角线 AC,BD 相交于点O,点 E 在 CA 的延长线上,OE=5,连接DE.
(1)线段AE 的长为 ;
(2)若 F 为 DE 的中点,则线段 AF 的长为
15.如图,□ABCD的对角线AC,BD 交于点O,分别以点B,C为圆心, AC, BD 长为半径画弧,两弧交于点 P,连接BP,CP.
(1)试判断四边形 BPCO 的形状,并说明理由.
(2)请说明当□ABCD 的对角线满足什么条件时,四边形 BPCO 是正方形
中小学教育资源及组卷应用平台
1. C [解析]对角线互相垂直平分的四边形是菱形,而不是正方形,故C选项符合题意.故选 C.
2.3 [解析]∵正方形对角线为6,∴①和②的直角边为3,∴矩形的长为6,宽为3,∴矩形的对角线长为
3.∵四边形ABCD是矩形,∴∠B=∠D=∠C=90°.
∵△AEF 是等边三角形,
∴AE=AF,∠AEF=∠AFE=60°.
∵∠CEF=45°,∴∠CFE=∠CEF=45°.
∴△AEB≌△AFD.∴AB=AD.
∴矩形ABCD 是正方形.
4.如图,连接AC交BD 于点O,过点 E 作EG⊥BD 于点G.
∵四边形 ABCD 是正方形,
∴∠AOG=90°.∵AE∥BD,
∴∠EAO=90°.又∠DGE=90°,
∴四边形 AOGE 是矩形.
∴∠EBD=30°.又BE=BD,
∵∠EFD=∠FDB+∠EBD=45°+30°=75°,
∴∠DEF=∠DFE.∴DF=DE.
5. A [解析]在正方形ABCD中,AD=AB,∠BAD=∠ABC=∠ADC=90°.
如图,将△ADF 绕点A 顺时针旋转90°,得△ABG,则AF=AG,∠DAF=∠BAG.
∵∠EAF=45°,∴∠BAE+∠DAF=45°,
∴∠GAE=∠FAE=45°.
在△FAE 和△GAE 中,
∴△FAE≌△GAE(SAS),∴∠AEF=∠AEG.
∵∠BAE=α,∴∠AEB=90°-α,
∴∠AEF=∠AEB=90°-α,
故选 A.
知识拓展 正方形的性质:1.四边相等且邻边相互垂直;2.对角线互相垂直平分且相等;3.每条对角线平分一组对角;4.每条对角线将正方形分为两个相等的等腰直角三角形;5.正方形既是轴对称图形,又是中心对称图形;6.正方形是邻边相等的特殊的矩形,是内角为直角的特殊的菱形.
6. [解析]如图,连接AE.
∵四边形ABCD 是正方形,
∴AB=AD,∠ABE=∠ADC=90°=∠ADF.
在△ABE 和△ADF 中,
∴△ABE≌△ADF(SAS),
∴AE=AF,∠DAF=∠BAE.
∵∠BAE+∠DAE=90°,
∴∠DAF+∠DAE=90°,
∴△EAF 是等腰直角三角形,∴∠AFG=45°.过点E作EH⊥BC交BD 于点 H.
∵∠DBC=45°,∠BEH=90°,
∴△BEH 是等腰直角三角形,
∴HE=BE=DF.
∵EH⊥BC,∴EH∥CD,
∴∠GHE=∠GDF,∠GEH=∠GFD,
∴△GHE≌△GDF,
∴EG=FG.
∵AE=AF,∴AG⊥FG,
∴△AGF 是等腰直角三角形.
7. [解析]在正方形 ABCD 中,对角线 AC 与 BD相交于点O,∴∠BCD=90°,O是BD的中点.
∵F为DE的中点,∴CF=EF=DF.
∵△CEF 的周长为32,CE=7,
∴CF+EF=25,即DE=25.
在 Rt△CDE中,根据勾股定理,得 ∴BE=24-7=17.
根据三角形的中位线定理,得
8.2 [解析]延长AF,DE 交于点 H,如图所示.
由图,得∠AFB=∠HFE.
∵∠BEC=2∠AFB,∴∠BEC=2∠HFE.
∵∠BEC=∠HFE+∠FHE,
∴∠HFE=∠FHE=∠AFB.
∵EF=1,∴EH=EF=1.
∵CE=3,∴CH=CE+EH=3+1=4.
∵四边形ABCD 为正方形,∴AB∥DH,
∴∠BAH=∠FHE,即∠BAH=∠AFB,
∴AB=BF.
设正方形ABCD边长为x,
则BC=x,AB=BF=x,BE=BF+FE=x+1.
∵△BCE 为直角三角形, 即 解得x=4.
在△ABG 和△HCG 中,
∴△ABG≌△HCG(ASA),∴CG=BG=2.
思路引导本题考查了正方形的性质、勾股定理、全等三角形的判定及性质、等腰三角形的判定,以利用条件“∠BEC=2∠AFB”和“AB∥DE”为突破口,想到添加辅助线“延长AF,DE 交于一点 H”是解题的关键.
9.(1)3 [解析]如图,过E 作EM⊥AD 于点M.
∴△ADE 的面积为
[解析]如图,过E 作 AD的垂线分别交AD,AG,BC于点M,N,P.
∵四边形ABCD 是正方形,∴BC∥AD,
∴EP⊥BC,∴四边形ABPM是矩形,
∴PM=AB=3,AB∥EP,
∴∠ABF=∠NEF.
∵F为BE 的中点,∴BF=EF.
在△ABF 与△NEF 中
∴△ABF≌△NEF(ASA),
∴EN=AB=3.
∴在 Rt△AEM中,
∴MN=1.
∵PM∥CD,∴AN=NG,
∴GD=2MN=2,
10. EF=CF+AE.理由如下:
延长FC到点P,使CP=AE,连接BP.
∵四边形ABCD 是正方形,
∴AB=BC,∠A=∠BCD=∠BCP=90°.
∵AE=CP,∴△ABE≌△CBP.
∴BE=BP,∠ABE=∠CBP.
∵∠ABC=∠ABE+∠EBC=90°,
∴∠CBP+∠EBC=90°,即∠EBP=90°.
∵∠EBF=45°,∴∠PBF=∠EBP-∠EBF=45°.
∴∠EBF=∠PBF=45°.
∵BE=BP,BF=BF,
∴△EBF≌△PBF.∴EF=PF.
∵PF=PC+CF,CP=AE,∴EF=CF+AE.
11.(1)如图,过点O作OH⊥AB 于点 H.
∵OF⊥AC于点F,OG⊥BC 于点G,
∴∠OGC=∠OFC=90°.
∴四边形OGCF 是矩形.
∵AD,BE 分别是∠BAC,∠ABC 的平分线,OF⊥AC,OG⊥BC,OH⊥AB,
∴OG=OH=OF.
又四边形OGCF 是矩形,
∴矩形 OGCF 是正方形.
(2)在 Rt△ABC 中,∵∠BAC=60°,
∴AB=2AC=2×4=8.
在 Rt△AOH 和 Rt△AOF 中,
∴Rt△AOH≌Rt△AOF(HL),
∴AH=AF,
设正方形OGCF 的边长为x,
则AH=AF=4-x,BH=BG=4 -x,
即正方形OGCF 的边长为
12.(1)∵四边形ABCD 是矩形,
∴∠DAB=∠ABC=90°.
∵DE⊥AF,∴∠DAB=∠AGD=90°.
∴∠BAF+∠DAF=90°,∠ADE+∠DAF=90°.
∴∠ADE=∠BAF.
∵DE=AF,∴△ADE≌△BAF.∴AD=AB.
∵四边形 ABCD 是矩形,
∴矩形 ABCD 是正方形.
(2)△AHF 是等腰三角形.理由如下:
∵四边形 ABCD 是正方形,
∴∠DAB=∠ABH=90°,AB=DA.
∵BH=AE,∴△DAE≌△ABH.∴AH=DE.
∵DE=AF,∴AH=AF.
∴△AHF是等腰三角形.
(3)如图,延长CB 到点 H,使BH=AE=6,连接AH.
∵四边形ABCD 是菱形,
∴AD∥BC,AB=AD.
∴∠ABH=∠BAD.
∵BH=AE,
∴△DAE≌△ABH.
∴AH=DE,∠H=∠AED=60°.
∵DE=AF,∴AH=AF.
∴△AHF 是等边三角形.
∴AH=HF=HB+BF=AE+BF=6+2=8.
∴DE=AH=8.
13.(1)∵四边形ABDI,四边形BCFE,四边形 ACHG都是正方形,
∴AC=AG,AB=BD,BC=BE,
∠GAC=∠EBC=∠DBA=90°.
∴∠ABC=∠EBD(同为∠EBA 的余角).
在△BDE 和△BAC中
∴△BDE≌△BAC(SAS).
(2)①∵△BDE≌△BAC,∠ADB=∠BAD=45°,∠BAC=α,∴∠EDA=α-45°,∠DAG=360°-45°-
②∵△BDE≌△BAC,
∴DE=AC=AG,∠BAC=∠BDE.
∵AD 是正方形ABDI 的对角线,
∴∠BDA=∠BAD=45°.
∵∠EDA=∠BDE-∠BDA=∠BDE-45°,由①,知∠DAG=225°-∠BAC.
180°.∴DE∥AG.
∴四边形ADEG 是平行四边形.
(3)当△ABC满足∠BAC=135°,且 时,四边形ADEG 是正方形.理由如下:
由①知,当∠BAC=135°时,∠DAG=90°.
∵四边形 ABDI 是正方形,
又四边形ACHG 是正方形,
∴当∠BAC=135°且. 时,四边形ADEG是正方形.
素养考向本题综合运用了正方形的判定与性质、全等三角形的判定与性质、平行四边形的性质、勾股定理等知识点.考查了推理能力和运算能力的核心素养.
14.(1)2 [解析]∵四边形ABCD 是正方形,∴OA=OC=OD=OB,∠DOC=90°,∴在 Rt△DOC 中, OC=OB=3.∵OE=5,∴AE=OE--OA=2.
[解析]如图,延长DA 到点G,使AG=AD,连接EG,过E作EH⊥AG 于点 H.
∵F 为DE 中点,A 为DG中点,∴AF 为△DGE 中位线,
在Rt△EAH 中,∠EAH=∠DAC=45°,∴AH=EH.
在 Rt△EGH 中,
难点突破 本题的难点是第(2)问,与线段AF有关的图形中的边、角的信息有AF 在△AED中,∠EAD= 点F 为DE的中点,AE=2,AD= 但直接利用这些信息都无法求出线段AF 的长,因此需要作出辅助线,“点F 为 DE 的中点”易联想到中位线定理,“∠EAD=135°”易联想到等腰直角三角形于是想到:延长 DA 到点G,使 AG=AD,连接EG,过点E 作EH⊥AG 于点 H.
15.(1)四边形 BPCO 为平行四边形.理由如下:
∵四边形ABCD 为平行四边形,
∵以点B,C为圆心, AC, BD长为半径画弧,两弧交于点 P,
∴OB=CP,BP=OC,
∴四边形 BPCO 为平行四边形.
(2)当AC⊥BD,AC=BD时,四边形BPCO 为正方形.
∵AC⊥BD,∴∠BOC=90°,
∵四边形 BPCO 为平行四边形,
∴平行四边形 BPCO 为正方形.
■知识拓展 本题考查了平行四边形的性质与判定、正方形的判定,熟练掌握以上知识是解题的关键.正方形的判定方法主要有:(1)对角线相等的菱形是正方形;(2)有一个角为直角的菱形是正方形;(3)对角线互相垂直的矩形是正方形;(4)一组邻边相等的矩形是正方形;(5)一组邻边相等且有一个角是直角的平行四边形是正方形;(6)对角线互相垂直且相等的平行四边形是正方形;(7)对角线相等且互相垂直平分的四边形是正方形;(8)一组邻边相等,有三个角是直角的四边形是正方形;(9)既是菱形又是矩形的四边形是正方形.
