特殊平行四边形的折叠问题专题提优特训10(含解析)
文档属性
| 名称 | 特殊平行四边形的折叠问题专题提优特训10(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 228.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-15 21:11:13 | ||
图片预览




文档简介
特殊平行四边形的折叠问题专题提优特训10
中小学教育资源及组卷应用平台
题型1 平行四边形的折叠问题
1.如图,将□ABCD 沿对角线AC 折叠,使点 B 落在点 B'处.若∠1=∠2=42°,则∠B 为( ).
A. 68° B. 106° C. 117° D. 126°
2.如图,在平行四边形 ABCD 中,BC=6cm,将△ABC 沿对角线AC 折叠,点 B 的对应点落在点E 处,边 BC 的对应边CE 与边AD 交于点F,此时△CDF 为等边三角形.
(1)求AB 的长;
(2)求图中阴影部分的面积.
题型2 矩形的折叠问题
3.(2024·陕西西安经开区期中)如图,在矩形ABCD中,E 是AD 的中点,∠EBC 的平分线交CD于点F,将△DEF 沿EF 折叠,点 D 恰好落在BE 上M 点处,延长BC,EF 交于点 N,有下列四个结论:①DF =CF;②BF⊥EN;③S△BEF=3S△DEF;④CN=DE.其中,正确的有 .
4.(2024·天津南开区二模)如图,将一张矩形纸片ABCD 折叠,折痕为 EF,折叠后,EC 的对应边EH 经过点A,CD 的对应边HG 交BA 的延长线于点 P.若PA=PG,AH=BE,CD=3,则 BC 的长为 .
5.如图(1),将矩形 ABCD 沿 DE 折叠,使顶点 A落在DC上的点A处,然后将矩形展平,沿EF折叠,使顶点A 落在折痕DE 上的点G 处,再将矩形 ABCD 沿CE 折叠,此时顶点 B 恰好落在DE 上的点 H 处,如图(2).
(1)求证:EG=CH;
(2)已知 求AD 和AB 的长.
6.对一张矩形纸片 ABCD 进行折叠,具体操作如下:
第一步:先对折,使AD 与BC 重合,得到折痕MN,展开;
第二步:再一次折叠,使点 A 落在MN 上的点A'处,并使折痕经过点 B,得到折痕BE,同时,得到线段BA',EA',展开,如图(1);
第三步:再沿 EA'所在的直线折叠,点B 落在AD 上的点B'处,得到折痕EF,同时得到线段B'F,展开,如图(2).求证:
(1)∠ABE=30°;
(2)四边形BFB'E 为菱形.
题型3 菱形的折叠问题
7.如图,将菱形纸片ABCD折叠,使点 A 恰好落在菱形的对称中心O处,折痕为EF,若菱形 ABCD 的边长为2cm,∠A=120°,则EF= cm.
8.(2024·安庆模拟)如图,在菱形ABCD 中,∠BAD=120°,点 E,F 分别在AB,BC上,将△BEF 沿EF 折叠,点 B 落在 AD 上的点 G 处,EG⊥AC.
(1)∠BEF= °,∠BFG= °.
(2)若 求FG的长.
题型4 正方形的折叠问题
9.中考新考法 最值问题 (2024·山东济宁梁山期末)如图,正方形纸片ABCD 的边长为 4 cm,点 M,N分别在边AB,CD 上.将该纸片沿 MN 折叠,使点 D 落在边 BC 上,落点为 E,MN 与DE相交于点Q.随着点M 的移动,点Q 移动路线长度的最大值是( ).
A. 2cm B. 4 cm C. cmD. 1cm
10.(2024·河南平顶山期末)如图,将一张边长为4 cm的正方形纸片ABCD 折叠,使点A 落在点 P处,折痕经过点 D 交边 AB 于点 E.连接BP,CP,若∠BPC=90°,则 AE 的长为 cm.
11.(2024·辽宁辽阳文圣区期中)如图,在矩形 ABCD中,AB=5,BC=6,点M,N 分别在AD,BC上,且3AM=AD,3BN=BC,E 为直线BC上一动点,连接DE,将△DCE 沿DE 所在直线翻折得到△DC'E,当点 C 恰好落在直线MN 上时,CE 的长为多少
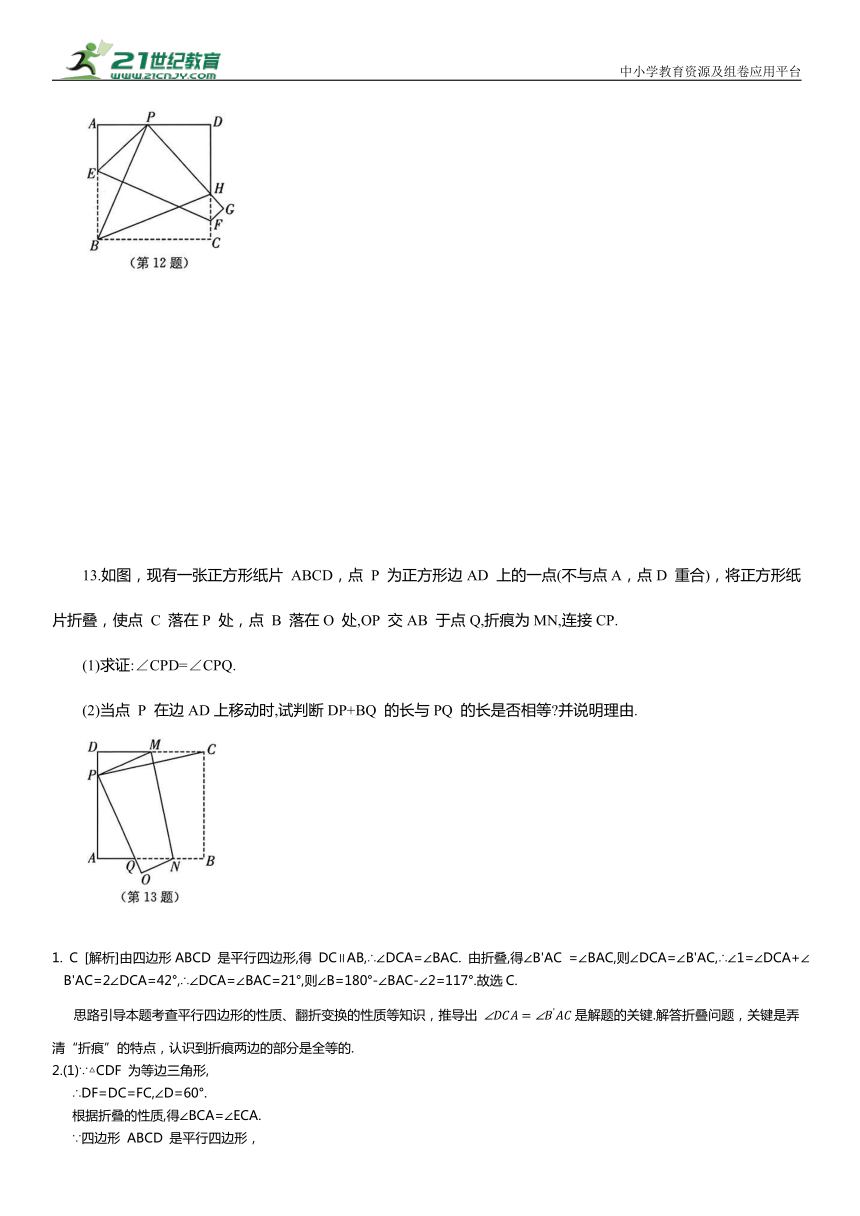
12.如图,现有一张边长为4 的正方形纸片AB-CD,点P 为正方形边AD 上的一点(不与点A,点D 重合),将正方形纸片折叠,使点 B落在点 P 处,点 C 落在G 处,PG 交DC 于点H,折痕为EF,连接BP,BH.
(1)求证:∠APB=∠BPH.
(2)当点 P 在边AD 上移动时,△PDH 的周
长是否发生变化 请证明你的结论.
13.如图,现有一张正方形纸片 ABCD,点 P 为正方形边AD 上的一点(不与点A,点D 重合),将正方形纸片折叠,使点 C 落在P 处,点 B 落在O 处,OP 交AB 于点Q,折痕为MN,连接CP.
(1)求证:∠CPD=∠CPQ.
(2)当点 P 在边AD上移动时,试判断DP+BQ 的长与PQ 的长是否相等 并说明理由.
1. C [解析]由四边形ABCD 是平行四边形,得 DC∥AB,∴∠DCA=∠BAC. 由折叠,得∠B'AC =∠BAC,则∠DCA=∠B'AC,∴∠1=∠DCA+∠B'AC=2∠DCA=42°,∴∠DCA=∠BAC=21°,则∠B=180°-∠BAC-∠2=117°.故选C.
思路引导本题考查平行四边形的性质、翻折变换的性质等知识,推导出 是解题的关键.解答折叠问题,关键是弄清“折痕”的特点,认识到折痕两边的部分是全等的.
2.(1)∵△CDF 为等边三角形,
∴DF=DC=FC,∠D=60°.
根据折叠的性质,得∠BCA=∠ECA.
∵四边形 ABCD 是平行四边形,
∴AD∥BC,AD=BC=6cm,AB=CD,
∴∠FAC=∠BCA,∴∠FAC=∠FCA,
∴FA=FC,∴∠DAC=30°,∴∠ACD=90°,
(2)∵CD=3cm,∠ACD=90°,∠DAC=30°,AD=
即图中阴影部分的面积为
3.①②③④
[解析]如图,连接PF,设B C=2x,AH=BE=a.
由矩形的性质和折叠的性质,知 FG=FD,∠G=∠FAP=90°,AB=CD=3,AD=BC.
∵PA=PG,PF=PF,
∴Rt△PAF≌Rt△PGF,
由矩形的性质,知AD∥BC,∴∠AFE=∠FEC. 由折叠的性质,知∠FEA=∠FEC,
∴∠FEA=∠AFE,∴AE=FA=x.
由折叠的性质,知EC=EH=AE+AH=x+a,∴BC=BE+EC=a+x+a=2x,
即
在 Rt△ABE 中, 即 3 + 解得
■ 思路引导 本题考查了矩形与折叠问题、全等三角形的判定和性质、勾股定理,运用数形结合的方法,熟练掌握各知识点进行推理与计算是解题的关键.
5.(1)由折叠的性质知,∠ADE=A'DE,AE=EG,BC=CH.
∵四边形ABCD 是矩形,∴AD=BC,AB∥CD.
∴∠A'DE=∠AED,∴∠AED=∠ADE,
∴AE=AD,∴EG=CH.
(2)∵∠ADE=45°,∠FGE=∠A=90°,AF= ∴DG= ,DF=2,∴AD=2+
如图,由折叠的性质知,∠1=∠2,∠3=∠4,
∴∠1+∠4=90°,∠2+∠3=90°.
∵∠1+∠AFE=90°,∴∠4=∠AFE.
又∠A=∠B=90°,由(1)知,AE=BC,
∴△EFA≌△CEB,∴AF=BE,∴AB=AE+
6.(1)∵对折,使AD与BC重合,折痕是MN,
∴点 M 是AB 的中点.∴A'是EF 的中点.
∵∠BA'E=∠A=90°,∴BA′垂直平分EF.
∴BE=BF.∴∠A'BE=∠A'BF.
由翻折的性质,得∠ABE=∠A'BE,
(2)∵沿 EA'所在的直线折叠,点 B 落在AD 上的点B'处,∴BE=B'E,BF=B'F.∵BE=BF, ,∴四边形 BFB'E为菱形.
7. [解析]连接BD,AC,由菱形性质可得菱形对称中心O为对角线AC与BD 的交点.
∵菱形对角线平分对角,∠A=120°,
∴∠ABO=30°,∠BAO=60°.
∵AB=2cm,∴AO=1cm,
由题意,得EF 为△ABD 的中位线,
■方法诠释 由菱形性质可知菱形的对称中心就是菱形对角线的交点,再根据特殊角得到 Rt△ABO中AO 的长,由勾股定理即可得到 BO 的长,即可得到BD 的长,再由折叠可得EF 为△ABD 的中位线,即可得解.
8.(1)75 90 [解析]∵四边形 ABCD 是菱形,∠BAD=120°,
∴AB=BC=CD=AD,∠CAB=∠CAD=60°,
∴△ABC,△ACD 是等边三角形.
∵EG⊥AC,∴∠AEG=∠AGE=30°.
由折叠的性质,得
∴∠BFG=90°.
(2)由(1),得∠AGE=30°,∠EGF=∠B=60°,∴∠AGF=90°,∴FG⊥BC.
过点 A 作AH⊥BC 于点H,则
∵FG⊥BC,AH⊥BC,∴AH∥FG.又 AD∥BC,
∴四边形AHFG 为平行四边形,
■思路引导 本题考查菱形的性质、等边三角形的判定和性质、对称变换、勾股定理等知识.(1)根据折叠的性质得出∠BEF=∠GEF,∠BFE=∠GFE,再利用三角形内角和解答即可.(2)过点 A 作 AH⊥BC 于点 H,由(1)中的条件证明四边形AHFG 为平行四边形,则 FG=AH,求出AH 即可.
9. A [解析]如图,取AB,CD 中点K,G,连接KG,BD 交于点O.
由题意知,点Q 移动的路线就是线段OG.
∴点 Q 移动路线长度的最大值是2cm .故选 A.
思路引导 本题考查正方形的性质、对称变换、三角形中位线定理等知识,解题的关键是找到点 Q 的移动路线.若点 D 落在边 BC 上,根据落点E 分别与点B,点C 重合时,即可找到点Q的运动路线.
10. [解析]如图,过点 P 作FG⊥AB 交AB 于点G,交CD于点F.
∵四边形ABCD 是正方形,∴ AB ∥CD,∴ 四 边形ADFG,GBCF 是矩形.
设DF=AG= xcm,
则CF=DC-DF=(4-x) cm,
过点 P 作PH⊥BC 于点 H,易得四边形 PHCF,PHBG是矩形,∴PH=CF=(4--x) cm.
设PF=CH= ycm,
则BH=BC-CH=(4-y) cm,
在 Rt△PBH 中,根据勾股定理,得
在Rt△PCH 中,根据勾股定理,得
在 Rt△PBC 中,根据勾股定理,得 =BC ,
整理,得 ①
在 Rt△PDF 中,根据勾股定理,得 ②
将②代入①,得16--8x--4y+16=0,∴y=8-2x,③
将③代入②,得
解得 (舍去),
设AE=t cm,则PE=t cm,∴EG=AB-BG-
在 Rt△PEG中,根据勾股定理,得
解得
思路引导 本题属于代数几何综合题,考查了对称变换、正方形的性质、矩形的判定与性质、勾股定理、一元二次方程,解决本题的关键是根据勾股定理列方程.
11.设CE=x,则(
当 E 点在线段BC 上时,如图(1).
∵在矩形ABCD中,AB=5,BC=6,
∴CD=AB=5,AD=BC=6,AD∥BC.
∵点 M,N 分别在 AD,BC 上,且 3AM=AD,3BN=BC,
∴DM=CN=4,∴四边形CDMN 为平行四边形.
∵∠NCD=90°,∴平行四边形 MNCD 是矩形,
∴∠DMN=∠MNC=90°,MN=CD=5.
由折叠,知C'D=CD=5,
∴C'N=5-3=2.
解得x=2.5,∴CE=2.5.当 E 点在CB 的延长线上时,如图(2),
∵矩形ABCD中,AB=5,BC=6
∴CD=AB=5,AD=BC=6,AD∥BC.
∵点 M,N 分别在AD,BC 上,且 3AM=AD,3BN=BC,∴DM=CN=4,∴四边形CDMN 为平行四边形.
∵∠NCD=90°,∴平行四边形 MNCD 是矩形,
∴∠DMN=∠MNC=90°,MN=CD=5.
由折叠,知
∴C'N=5+3=8.
,解得x=10,
∴CE=10.
综上所述,CE=2.5或10.
易错警示 本题考查了对称变换、矩形的性质与判定、勾股定理、一元二次方程的应用,解答本题容易出现的错误是受给出图形的影响,没有领会题目条件“E为直线 BC 上一动点”,因此只考虑E 点在线段BC上这种情况,而忽视了E 点也可能在CB的延长线上.
12.(1)∵PE=BE,∴∠EBP=∠EPB.
又∠EPH=∠EBC=90°,
∴∠EPH-∠EPB=∠EBC-∠EBP,
即∠PBC=∠BPH.
又AD∥BC,∴∠APB=∠PBC.
∴∠APB=∠BPH.
(2)△PHD 的周长不变,为定值8.证明如下:过点 B 作BQ⊥PH,垂足为Q.
由(1)知∠APB=∠BPH,
在△ABP 和△QBP 中
∴△ABP≌△QBP(AAS).∴AP=QP,AB=QB.又AB=BC,∴BC=BQ.
又∠C=∠BQH=90°,BH=BH,
∴Rt△BCH≌Rt△BQH,∴CH=QH,
∴△PHD 的周长=PD+DH+PH=PD+DH+AP+HC=AD+CD=8.
13.(1)由翻折变换的性质,得∠PCB=∠CPQ.
∵四边形ABCD为正方形,
∴AD∥BC,∴∠CPD=∠PCB.
∴∠CPD=∠CPQ.
(2)DP+BQ=PQ.理由如下:
过点 C作CE⊥PO,垂足为 E,连接CQ.
由(1)知,∠CPD=∠CPQ,
在△CDP 和△CEP 中
∴△CDP≌△CEP(AAS),∴CD=CE,DP=EP,
∴BC=EC.又∠B=∠CEQ=90°,
∴△CEQ 和△CBQ 都是直角三角形.
在 Rt△CEQ与 Rt△CBQ中,
∴Rt△CEQ≌Rt△CBQ.
∴EQ=BQ,∴DP+BQ=PQ.
中小学教育资源及组卷应用平台
题型1 平行四边形的折叠问题
1.如图,将□ABCD 沿对角线AC 折叠,使点 B 落在点 B'处.若∠1=∠2=42°,则∠B 为( ).
A. 68° B. 106° C. 117° D. 126°
2.如图,在平行四边形 ABCD 中,BC=6cm,将△ABC 沿对角线AC 折叠,点 B 的对应点落在点E 处,边 BC 的对应边CE 与边AD 交于点F,此时△CDF 为等边三角形.
(1)求AB 的长;
(2)求图中阴影部分的面积.
题型2 矩形的折叠问题
3.(2024·陕西西安经开区期中)如图,在矩形ABCD中,E 是AD 的中点,∠EBC 的平分线交CD于点F,将△DEF 沿EF 折叠,点 D 恰好落在BE 上M 点处,延长BC,EF 交于点 N,有下列四个结论:①DF =CF;②BF⊥EN;③S△BEF=3S△DEF;④CN=DE.其中,正确的有 .
4.(2024·天津南开区二模)如图,将一张矩形纸片ABCD 折叠,折痕为 EF,折叠后,EC 的对应边EH 经过点A,CD 的对应边HG 交BA 的延长线于点 P.若PA=PG,AH=BE,CD=3,则 BC 的长为 .
5.如图(1),将矩形 ABCD 沿 DE 折叠,使顶点 A落在DC上的点A处,然后将矩形展平,沿EF折叠,使顶点A 落在折痕DE 上的点G 处,再将矩形 ABCD 沿CE 折叠,此时顶点 B 恰好落在DE 上的点 H 处,如图(2).
(1)求证:EG=CH;
(2)已知 求AD 和AB 的长.
6.对一张矩形纸片 ABCD 进行折叠,具体操作如下:
第一步:先对折,使AD 与BC 重合,得到折痕MN,展开;
第二步:再一次折叠,使点 A 落在MN 上的点A'处,并使折痕经过点 B,得到折痕BE,同时,得到线段BA',EA',展开,如图(1);
第三步:再沿 EA'所在的直线折叠,点B 落在AD 上的点B'处,得到折痕EF,同时得到线段B'F,展开,如图(2).求证:
(1)∠ABE=30°;
(2)四边形BFB'E 为菱形.
题型3 菱形的折叠问题
7.如图,将菱形纸片ABCD折叠,使点 A 恰好落在菱形的对称中心O处,折痕为EF,若菱形 ABCD 的边长为2cm,∠A=120°,则EF= cm.
8.(2024·安庆模拟)如图,在菱形ABCD 中,∠BAD=120°,点 E,F 分别在AB,BC上,将△BEF 沿EF 折叠,点 B 落在 AD 上的点 G 处,EG⊥AC.
(1)∠BEF= °,∠BFG= °.
(2)若 求FG的长.
题型4 正方形的折叠问题
9.中考新考法 最值问题 (2024·山东济宁梁山期末)如图,正方形纸片ABCD 的边长为 4 cm,点 M,N分别在边AB,CD 上.将该纸片沿 MN 折叠,使点 D 落在边 BC 上,落点为 E,MN 与DE相交于点Q.随着点M 的移动,点Q 移动路线长度的最大值是( ).
A. 2cm B. 4 cm C. cmD. 1cm
10.(2024·河南平顶山期末)如图,将一张边长为4 cm的正方形纸片ABCD 折叠,使点A 落在点 P处,折痕经过点 D 交边 AB 于点 E.连接BP,CP,若∠BPC=90°,则 AE 的长为 cm.
11.(2024·辽宁辽阳文圣区期中)如图,在矩形 ABCD中,AB=5,BC=6,点M,N 分别在AD,BC上,且3AM=AD,3BN=BC,E 为直线BC上一动点,连接DE,将△DCE 沿DE 所在直线翻折得到△DC'E,当点 C 恰好落在直线MN 上时,CE 的长为多少
12.如图,现有一张边长为4 的正方形纸片AB-CD,点P 为正方形边AD 上的一点(不与点A,点D 重合),将正方形纸片折叠,使点 B落在点 P 处,点 C 落在G 处,PG 交DC 于点H,折痕为EF,连接BP,BH.
(1)求证:∠APB=∠BPH.
(2)当点 P 在边AD 上移动时,△PDH 的周
长是否发生变化 请证明你的结论.
13.如图,现有一张正方形纸片 ABCD,点 P 为正方形边AD 上的一点(不与点A,点D 重合),将正方形纸片折叠,使点 C 落在P 处,点 B 落在O 处,OP 交AB 于点Q,折痕为MN,连接CP.
(1)求证:∠CPD=∠CPQ.
(2)当点 P 在边AD上移动时,试判断DP+BQ 的长与PQ 的长是否相等 并说明理由.
1. C [解析]由四边形ABCD 是平行四边形,得 DC∥AB,∴∠DCA=∠BAC. 由折叠,得∠B'AC =∠BAC,则∠DCA=∠B'AC,∴∠1=∠DCA+∠B'AC=2∠DCA=42°,∴∠DCA=∠BAC=21°,则∠B=180°-∠BAC-∠2=117°.故选C.
思路引导本题考查平行四边形的性质、翻折变换的性质等知识,推导出 是解题的关键.解答折叠问题,关键是弄清“折痕”的特点,认识到折痕两边的部分是全等的.
2.(1)∵△CDF 为等边三角形,
∴DF=DC=FC,∠D=60°.
根据折叠的性质,得∠BCA=∠ECA.
∵四边形 ABCD 是平行四边形,
∴AD∥BC,AD=BC=6cm,AB=CD,
∴∠FAC=∠BCA,∴∠FAC=∠FCA,
∴FA=FC,∴∠DAC=30°,∴∠ACD=90°,
(2)∵CD=3cm,∠ACD=90°,∠DAC=30°,AD=
即图中阴影部分的面积为
3.①②③④
[解析]如图,连接PF,设B C=2x,AH=BE=a.
由矩形的性质和折叠的性质,知 FG=FD,∠G=∠FAP=90°,AB=CD=3,AD=BC.
∵PA=PG,PF=PF,
∴Rt△PAF≌Rt△PGF,
由矩形的性质,知AD∥BC,∴∠AFE=∠FEC. 由折叠的性质,知∠FEA=∠FEC,
∴∠FEA=∠AFE,∴AE=FA=x.
由折叠的性质,知EC=EH=AE+AH=x+a,∴BC=BE+EC=a+x+a=2x,
即
在 Rt△ABE 中, 即 3 + 解得
■ 思路引导 本题考查了矩形与折叠问题、全等三角形的判定和性质、勾股定理,运用数形结合的方法,熟练掌握各知识点进行推理与计算是解题的关键.
5.(1)由折叠的性质知,∠ADE=A'DE,AE=EG,BC=CH.
∵四边形ABCD 是矩形,∴AD=BC,AB∥CD.
∴∠A'DE=∠AED,∴∠AED=∠ADE,
∴AE=AD,∴EG=CH.
(2)∵∠ADE=45°,∠FGE=∠A=90°,AF= ∴DG= ,DF=2,∴AD=2+
如图,由折叠的性质知,∠1=∠2,∠3=∠4,
∴∠1+∠4=90°,∠2+∠3=90°.
∵∠1+∠AFE=90°,∴∠4=∠AFE.
又∠A=∠B=90°,由(1)知,AE=BC,
∴△EFA≌△CEB,∴AF=BE,∴AB=AE+
6.(1)∵对折,使AD与BC重合,折痕是MN,
∴点 M 是AB 的中点.∴A'是EF 的中点.
∵∠BA'E=∠A=90°,∴BA′垂直平分EF.
∴BE=BF.∴∠A'BE=∠A'BF.
由翻折的性质,得∠ABE=∠A'BE,
(2)∵沿 EA'所在的直线折叠,点 B 落在AD 上的点B'处,∴BE=B'E,BF=B'F.∵BE=BF, ,∴四边形 BFB'E为菱形.
7. [解析]连接BD,AC,由菱形性质可得菱形对称中心O为对角线AC与BD 的交点.
∵菱形对角线平分对角,∠A=120°,
∴∠ABO=30°,∠BAO=60°.
∵AB=2cm,∴AO=1cm,
由题意,得EF 为△ABD 的中位线,
■方法诠释 由菱形性质可知菱形的对称中心就是菱形对角线的交点,再根据特殊角得到 Rt△ABO中AO 的长,由勾股定理即可得到 BO 的长,即可得到BD 的长,再由折叠可得EF 为△ABD 的中位线,即可得解.
8.(1)75 90 [解析]∵四边形 ABCD 是菱形,∠BAD=120°,
∴AB=BC=CD=AD,∠CAB=∠CAD=60°,
∴△ABC,△ACD 是等边三角形.
∵EG⊥AC,∴∠AEG=∠AGE=30°.
由折叠的性质,得
∴∠BFG=90°.
(2)由(1),得∠AGE=30°,∠EGF=∠B=60°,∴∠AGF=90°,∴FG⊥BC.
过点 A 作AH⊥BC 于点H,则
∵FG⊥BC,AH⊥BC,∴AH∥FG.又 AD∥BC,
∴四边形AHFG 为平行四边形,
■思路引导 本题考查菱形的性质、等边三角形的判定和性质、对称变换、勾股定理等知识.(1)根据折叠的性质得出∠BEF=∠GEF,∠BFE=∠GFE,再利用三角形内角和解答即可.(2)过点 A 作 AH⊥BC 于点 H,由(1)中的条件证明四边形AHFG 为平行四边形,则 FG=AH,求出AH 即可.
9. A [解析]如图,取AB,CD 中点K,G,连接KG,BD 交于点O.
由题意知,点Q 移动的路线就是线段OG.
∴点 Q 移动路线长度的最大值是2cm .故选 A.
思路引导 本题考查正方形的性质、对称变换、三角形中位线定理等知识,解题的关键是找到点 Q 的移动路线.若点 D 落在边 BC 上,根据落点E 分别与点B,点C 重合时,即可找到点Q的运动路线.
10. [解析]如图,过点 P 作FG⊥AB 交AB 于点G,交CD于点F.
∵四边形ABCD 是正方形,∴ AB ∥CD,∴ 四 边形ADFG,GBCF 是矩形.
设DF=AG= xcm,
则CF=DC-DF=(4-x) cm,
过点 P 作PH⊥BC 于点 H,易得四边形 PHCF,PHBG是矩形,∴PH=CF=(4--x) cm.
设PF=CH= ycm,
则BH=BC-CH=(4-y) cm,
在 Rt△PBH 中,根据勾股定理,得
在Rt△PCH 中,根据勾股定理,得
在 Rt△PBC 中,根据勾股定理,得 =BC ,
整理,得 ①
在 Rt△PDF 中,根据勾股定理,得 ②
将②代入①,得16--8x--4y+16=0,∴y=8-2x,③
将③代入②,得
解得 (舍去),
设AE=t cm,则PE=t cm,∴EG=AB-BG-
在 Rt△PEG中,根据勾股定理,得
解得
思路引导 本题属于代数几何综合题,考查了对称变换、正方形的性质、矩形的判定与性质、勾股定理、一元二次方程,解决本题的关键是根据勾股定理列方程.
11.设CE=x,则(
当 E 点在线段BC 上时,如图(1).
∵在矩形ABCD中,AB=5,BC=6,
∴CD=AB=5,AD=BC=6,AD∥BC.
∵点 M,N 分别在 AD,BC 上,且 3AM=AD,3BN=BC,
∴DM=CN=4,∴四边形CDMN 为平行四边形.
∵∠NCD=90°,∴平行四边形 MNCD 是矩形,
∴∠DMN=∠MNC=90°,MN=CD=5.
由折叠,知C'D=CD=5,
∴C'N=5-3=2.
解得x=2.5,∴CE=2.5.当 E 点在CB 的延长线上时,如图(2),
∵矩形ABCD中,AB=5,BC=6
∴CD=AB=5,AD=BC=6,AD∥BC.
∵点 M,N 分别在AD,BC 上,且 3AM=AD,3BN=BC,∴DM=CN=4,∴四边形CDMN 为平行四边形.
∵∠NCD=90°,∴平行四边形 MNCD 是矩形,
∴∠DMN=∠MNC=90°,MN=CD=5.
由折叠,知
∴C'N=5+3=8.
,解得x=10,
∴CE=10.
综上所述,CE=2.5或10.
易错警示 本题考查了对称变换、矩形的性质与判定、勾股定理、一元二次方程的应用,解答本题容易出现的错误是受给出图形的影响,没有领会题目条件“E为直线 BC 上一动点”,因此只考虑E 点在线段BC上这种情况,而忽视了E 点也可能在CB的延长线上.
12.(1)∵PE=BE,∴∠EBP=∠EPB.
又∠EPH=∠EBC=90°,
∴∠EPH-∠EPB=∠EBC-∠EBP,
即∠PBC=∠BPH.
又AD∥BC,∴∠APB=∠PBC.
∴∠APB=∠BPH.
(2)△PHD 的周长不变,为定值8.证明如下:过点 B 作BQ⊥PH,垂足为Q.
由(1)知∠APB=∠BPH,
在△ABP 和△QBP 中
∴△ABP≌△QBP(AAS).∴AP=QP,AB=QB.又AB=BC,∴BC=BQ.
又∠C=∠BQH=90°,BH=BH,
∴Rt△BCH≌Rt△BQH,∴CH=QH,
∴△PHD 的周长=PD+DH+PH=PD+DH+AP+HC=AD+CD=8.
13.(1)由翻折变换的性质,得∠PCB=∠CPQ.
∵四边形ABCD为正方形,
∴AD∥BC,∴∠CPD=∠PCB.
∴∠CPD=∠CPQ.
(2)DP+BQ=PQ.理由如下:
过点 C作CE⊥PO,垂足为 E,连接CQ.
由(1)知,∠CPD=∠CPQ,
在△CDP 和△CEP 中
∴△CDP≌△CEP(AAS),∴CD=CE,DP=EP,
∴BC=EC.又∠B=∠CEQ=90°,
∴△CEQ 和△CBQ 都是直角三角形.
在 Rt△CEQ与 Rt△CBQ中,
∴Rt△CEQ≌Rt△CBQ.
∴EQ=BQ,∴DP+BQ=PQ.
