19.2.2平行四边形(2)提优训练 (含答案)
文档属性
| 名称 | 19.2.2平行四边形(2)提优训练 (含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 167.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-15 00:00:00 | ||
图片预览


文档简介
19.2.2平行四边形(2)
中小学教育资源及组卷应用平台
1.(2024·乐山中考)如图,下列条件中不能判定四边形 ABCD 为平行四边形的是( ).
A. AB∥DC,AD∥BC
B. AB=DC,AD=BC
C. AO=CO,BO=DO
D. AB∥DC,AD=BC
2. 教材 P80思考T1·变式 (2024·山东临沂兰陵期末)已知四边形的四条边长分别为a,b,c,d,其中a,c为一组对边的边长,且满足 则四边形一定是( ).
A.任意四边形
B.平行四边形
C.对角线相等的四边形
D. 无法确定
3.中考新考法 添加条件开放 如图,请在下列四个关系中,选出两个恰当的关系作为条件,推出四边形 ABCD 是平行四边形,并予以证明.(写出一种即可)
关系:①AD∥BC;②AB=CD;③∠A=∠C;④∠B+∠C=180°.
已知:在四边形 ABCD 中, , .
求证:四边形ABCD 是平行四边形.
4. 如图,在 ABCD 中,点 E,F在AC上,且AE=CF.求证:四边形BEDF是平行四边形.
5. 如图,在 AMCN 中,对角线 AC,MN 交于点O,点 B 和点 D分别在OM,ON 的延长线上.添加以下条件,不能说明四边形ABCD是平行四边形的是( ).
A. AB=AD B. AD∥BC
C. BM=DN D. ∠MAB=∠NCD
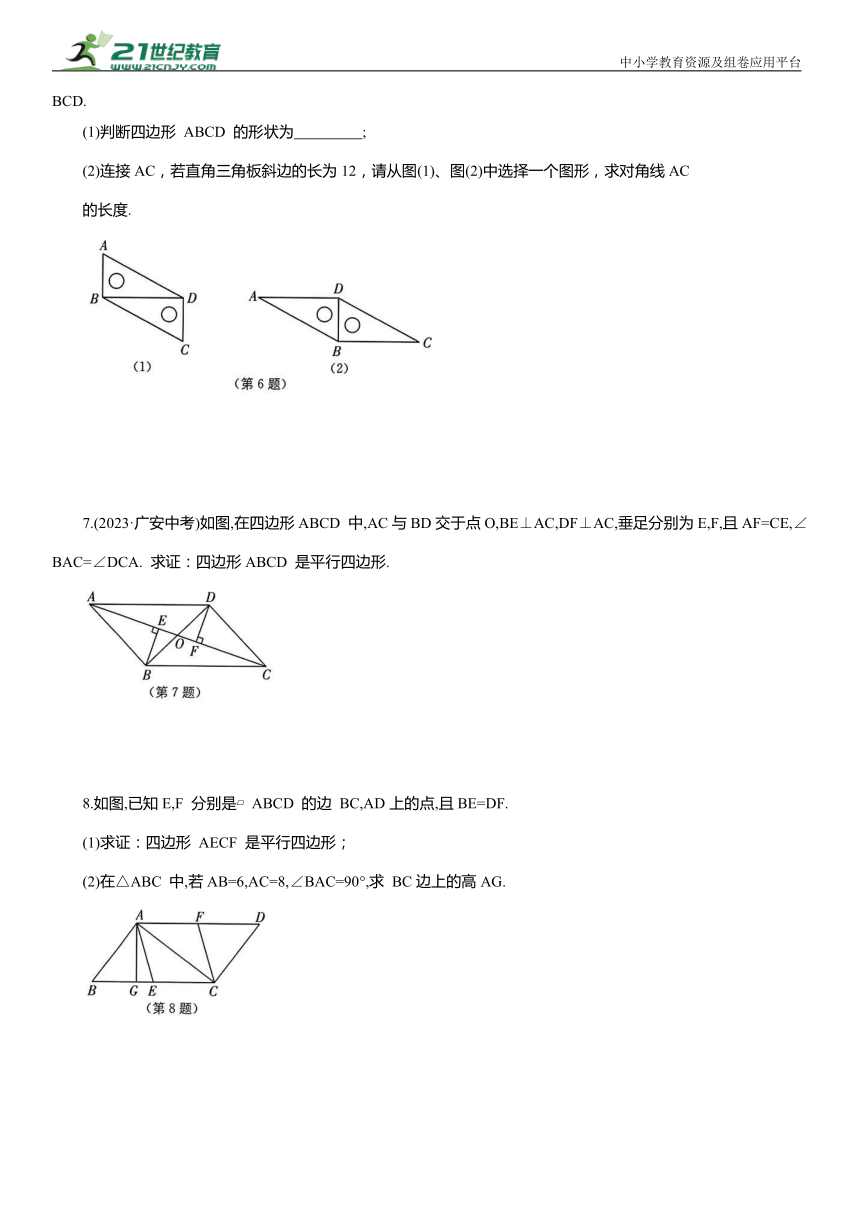
6.(2024·贵州遵义二模)如图,佳佳将两个全等的直角三角板(含30°)的直角边重合拼成如图(1)、图(2)的四边形ABCD.
(1)判断四边形 ABCD 的形状为 ;
(2)连接AC,若直角三角板斜边的长为12,请从图(1)、图(2)中选择一个图形,求对角线AC
的长度.
7.(2023·广安中考)如图,在四边形ABCD 中,AC与BD交于点O,BE⊥AC,DF⊥AC,垂足分别为E,F,且AF=CE,∠BAC=∠DCA. 求证:四边形ABCD 是平行四边形.
8.如图,已知E,F 分别是 ABCD 的边 BC,AD上的点,且BE=DF.
(1)求证:四边形 AECF 是平行四边形;
(2)在△ABC 中,若AB=6,AC=8,∠BAC=90°,求 BC边上的高AG.
9.(2024·浙江绍兴柯桥区期末)已知△ABC 和△ADE均为等边三角形,点 F,D 分别在AC,BC上,AF=CD,连接BF,EF.求证:
(1)AD=BF;
(2)四边形 BFED 为平行四边形.
10.中考新考法 动点问题 如图,在四边形ABCD 中,AD∥BC,AD=12cm,BC=15 cm,点 P 自点A 向点D 以1cm/s的速度运动,到 D 点即停止.点 Q 自点C 向B 以2cm/s的速度运动,到B 点即停止,点P,Q同时出发,设运动时间为t(s).
(1)用含 t 的代数式表示:AP = ;DP= ;BQ= ;CQ= .
(2)当t 为何值时,四边形APQB 是平行四边形
(3)当t 为何值时,四边形 PDCQ 是平行四边形
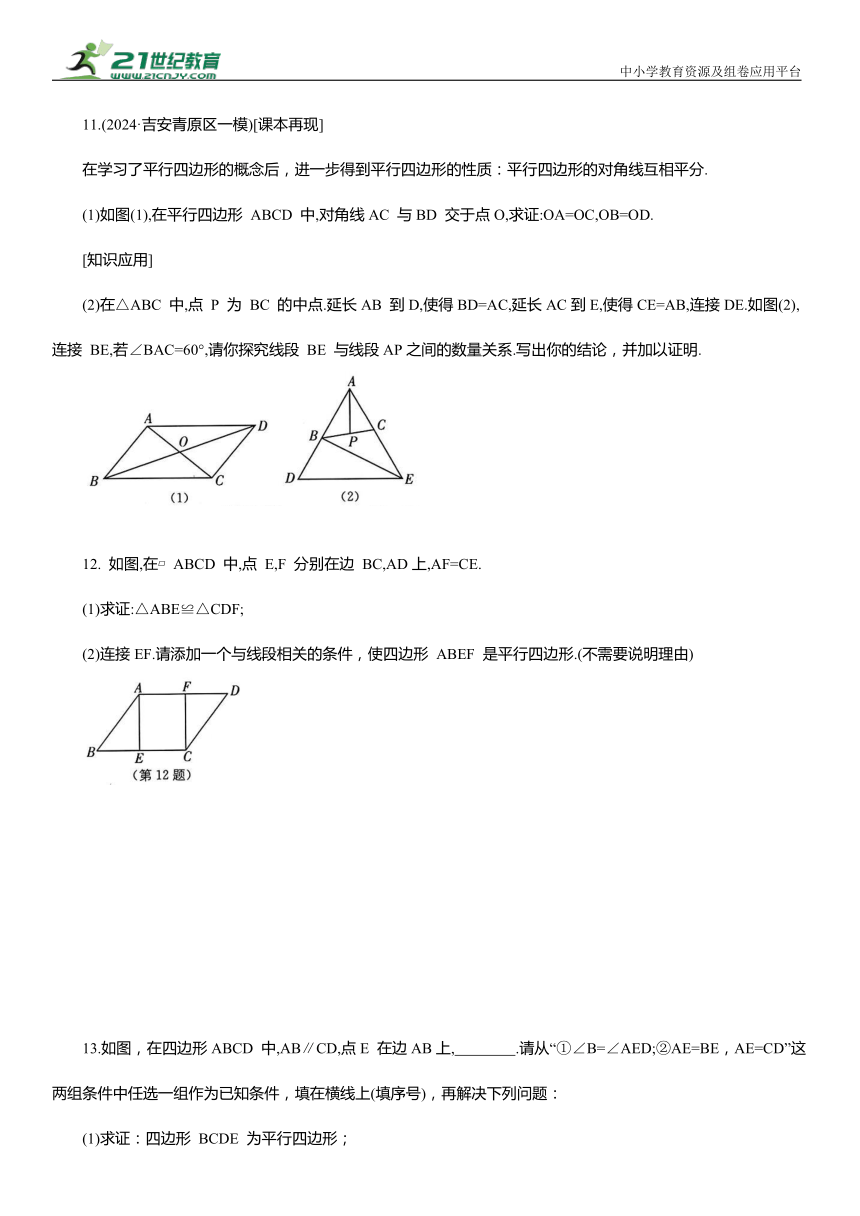
11.(2024·吉安青原区一模)[课本再现]
在学行四边形的概念后,进一步得到平行四边形的性质:平行四边形的对角线互相平分.
(1)如图(1),在平行四边形 ABCD 中,对角线AC 与BD 交于点O,求证:OA=OC,OB=OD.
[知识应用]
(2)在△ABC 中,点 P 为 BC 的中点.延长AB 到D,使得BD=AC,延长AC到E,使得CE=AB,连接DE.如图(2),连接 BE,若∠BAC=60°,请你探究线段 BE 与线段AP之间的数量关系.写出你的结论,并加以证明.
12. 如图,在 ABCD 中,点 E,F 分别在边 BC,AD上,AF=CE.
(1)求证:△ABE≌△CDF;
(2)连接EF.请添加一个与线段相关的条件,使四边形 ABEF 是平行四边形.(不需要说明理由)
13.如图,在四边形ABCD 中,AB∥CD,点E 在边AB上, .请从“①∠B=∠AED;②AE=BE,AE=CD”这两组条件中任选一组作为已知条件,填在横线上(填序号),再解决下列问题:
(1)求证:四边形 BCDE 为平行四边形;
(2)若AD⊥AB,AD=8,BC=10,求线段AE的长.
第2课时 平行四边形(2)
1. D [解析]选项 A符合“两组对边分别平行的四边形是平行四边形”的判定定理,故它能判断这个四边形是平行四边形,不符合题意;选项 B符合“两组对边分别相等的四边形是平行四边形”的判定定理,故它能判断这个四边形是平行四边形,不符合题意;选项C符合“对角线互相平分的四边形是平行四边形”的判定定理,故它能判断这个四边形是平行四边形,不符合题意;因为一组对边平行,另一组对边相等,可能是等腰梯形,所以选项D不能判断这个四边形是平行四边形,符合题意.故选 D.
2. B [解析]把原式变形为 ∵(a-c) ≥0,√b-d≥0,∴a-c=0,b-d=0,∴a=c,b=d,∴该四边形为平行四边形.故选 B.
3.答案不唯一,已知条件可选①③或①④或②④或③④均可.
选择①③:已知:在四边形ABCD中,①AD∥BC,③∠A=∠C.
求证:四边形 ABCD 是平行四边形.
证明:∵AD∥BC,∴∠A+∠B=180°.
∵∠A=∠C,∴∠B+∠C=180°,
∴AB∥CD,∴四边形ABCD 是平行四边形.
选择①④:
已知:在四边形 ABCD 中,①AD∥BC,④∠B+∠C=180°.
求证:四边形 ABCD 是平行四边形.
证明:∵∠B+∠C=180°,∴AB∥CD.又AD∥BC,∴四边形ABCD 是平行四边形.
选择②④:已知:在四边形ABCD中,②AB=CD,④∠B+∠C=180°.
求证:四边形ABCD 是平行四边形.
证明:∵∠B+∠C=180°,∴AB∥CD.
又AB=CD,∴四边形ABCD 是平行四边形.
选择③④:已知:在四边形ABCD 中,③∠A=∠C,④∠B+∠C=180°.
求证:四边形ABCD 是平行四边形.
证明:∵∠B+∠C=180°,∴AB∥CD.
∵∠A=∠C,∴∠A+∠B=180°,∴AD∥BC,
∴四边形ABCD 是平行四边形.
4.如图,连接 BD,与 AC 交于点O.
∵四边形 ABCD 是平行四边形,
∴OA=OC,OB=OD.
∵AE=CF,∴OA-AE=OC-CF,
∴OE=OF,∴四边形BEDF 是平行四边形.
5. A [解析]在□AMCN中,AO=OC,OM=ON.
A.添加AB=AD,不能说明四边形ABCD 是平行四边形,故符合题意;
B.∵AD∥BC,∴∠ADB=∠CBD.
∵AO=CO,∠AOD=∠COB,
∴△AOD≌△COB(AAS),∴OB=OD,
∴四边形 ABCD 是平行四边形,故B 不符合题意;
C.∵BM=DN,∴BM+OM=ON+DN,即OB=OD.∵AO=CO,
∴四边形 ABCD 是平行四边形,故C 不符合题意;
D.∵四边形AMCN 是平行四边形,
∴AM=CN,AM∥CN,∴∠AMO=∠CNO,
∴∠AMB=∠CND.
∵∠BAM=∠DCN,∴△ABM≌△CDN(ASA).
∴AB=CD,∠ABM=∠CDN,∴AB∥CD,
∴四边形ABCD 是平行四边形.故D不符合题意.故选A.
6.(1)平行四边形
(2)选择题图(1),连接AC,设AC和BD 交于点O.
∵∠CBD=30°,∠CDB=90°,BC=12,
∵四边形ABCD 是平行四边形,
7.∵BE⊥AC,DF⊥AC,∴∠AEB=∠DFC=90°.
∵AF=CE,∴AF--EF=CE--EF,∴AE=CF.
在△ABE 与△CDF 中,
∴△ABE≌△CDF(ASA),∴AB=CD.
∵∠BAC=∠DCA,∴AB∥CD,
∴四边形ABCD 是平行四边形.
8.(1)∵四边形ABCD 是平行四边形,
∴AD∥BC,且AD=BC,∴AF∥EC.
∵BE=DF,∴AD-DF=BC--BE,
即AF=EC,∴四边形AECF 是平行四边形.
(2)∵AB=6,AC=8,∠BAC=90°,
∵AG是BC 边上的高,
即 BC 边上的高AG 为
归纳总结本题考查了平行四边形的判定与性质、勾股定理以及三角形面积等知识,熟练掌握平行四边形的判定与性质和勾股定理是解题的关键.
9.(1)∵△ABC为等边三角形,
∴AB=AC,∠BAF=∠C=60°.
∵AF=CD,∴△ABF≌△CAD(SAS),
∴∠ABF=∠CAD,AD=BF.
(2)如图,设AC与DE 相交于点 H,由(1)知,BF=AD.
∵△ADE 是等边三角形,∴AD=DE,
∴BF=DE.
∵∠C=∠AED=60°,∠DHC=∠AHE,
∴∠CDH=∠CAE.
∵∠CAE+∠DAC=∠CBF+∠ABF=60°,∠ABF=∠DAC,
∴∠CBF=∠CAE,∴∠CBF=∠CDH,∴BF∥DE,
∴四边形 BFED 为平行四边形.
■归纳总结 本题考查了平行四边形的判定、等边三角形的性质、全等三角形的判定与性质.灵活运用平行四边形的判定、等边三角形的性质、全等三角形的判定与性质是解题的关键.
10.(1)t cm (12-t) cm (15-2t) cm 2t cm
(2)∵AD∥BC,∴当AP=BQ时,四边形APQB 是平行四边形,∴t=15-2t,解得t=5,
∴当t=5时,四边形APQB 是平行四边形.
(3)∵AD∥BC,即PD∥CQ,
∴当 PD=QC 时,四边形 PDCQ 是平行四边形,即12-t=2t,解得t=4,
∴当t=4时,四边形 PDCQ 是平行四边形.
11.(1)∵四边形ABCD 是平行四边形,
∴AD=BC,AD∥BC,
∴∠OAD=∠OCB,∠ODA=∠OBC,
∴△OAD≌△OCB(ASA),∴OA=OC,OB=OD.
(2)BE=2AP,证明如下:如图所示,过点 B 作 BH∥AE交DE 于点 H,连接PH,CH,
∴∠DBH=∠BAC=60°.
∵AB=CE,AC=BD,
∴AB+BD=AC+CE,即AD=AE,
∴△ADE 是等边三角形,∴∠D=60°,DE=DA,
∴△DBH 是等边三角形,
∴BH=BD=DH,∴BH=AC.
∵BH∥AC,
∴四边形ABHC是平行四边形,
∴AH,BC 互相平分.∵点 P 为BC 的中点,
∴A,P,H 三点共线,∴AH=2AP,
在△ADH 和△EDB 中,
∴△ADH≌△EDB(SAS),
∴BE=AH,∴BE=2AP.
■解后反思 本题考查了平行四边形的性质与判定、全等三角形的性质与判定、等边三角形的性质与判定等,关键是平行四边形判定定理的应用.
12.(1)∵四边形 ABCD 是平行四边形,
∴AB=CD,AD=BC,∠B=∠D.
∵AF=CE,∴AD-AF=BC-CE,
∴DF=BE.
在△ABE与△CDF中,
∴△ABE≌△CDF(SAS).
(2)添加 BE=CE(答案不唯一).理由如下:如图,∵AF=CE,BE=CE,∴AF=BE.
∵四边形ABCD 是平行四边形,
∴AD∥BC,∴AF∥BE,
∴四边形 ABEF 是平行四边形.
■ 易错警示 本题考查了平行四边形的判定与性质以及全等三角形的判定与性质等知识,熟练掌握平行四边形的判定与性质是解题的关键.注意第(2)题添加的条件不唯一.
13.(1)选择①,∵∠B=∠AED,∴BC∥DE.
∵AB∥CD,∴四边形BCDE 为平行四边形.
选择②,∵AE=BE,AE=CD,∴BE=CD,
∵AB∥CD,∴四边形BCDE 为平行四边形.
(2)由(1)可知,四边形 BCDE 为平行四边形,
∴DE=BC=10.∵AD⊥AB,∴∠A=90°,
即线段AE 的长为6.
中小学教育资源及组卷应用平台
1.(2024·乐山中考)如图,下列条件中不能判定四边形 ABCD 为平行四边形的是( ).
A. AB∥DC,AD∥BC
B. AB=DC,AD=BC
C. AO=CO,BO=DO
D. AB∥DC,AD=BC
2. 教材 P80思考T1·变式 (2024·山东临沂兰陵期末)已知四边形的四条边长分别为a,b,c,d,其中a,c为一组对边的边长,且满足 则四边形一定是( ).
A.任意四边形
B.平行四边形
C.对角线相等的四边形
D. 无法确定
3.中考新考法 添加条件开放 如图,请在下列四个关系中,选出两个恰当的关系作为条件,推出四边形 ABCD 是平行四边形,并予以证明.(写出一种即可)
关系:①AD∥BC;②AB=CD;③∠A=∠C;④∠B+∠C=180°.
已知:在四边形 ABCD 中, , .
求证:四边形ABCD 是平行四边形.
4. 如图,在 ABCD 中,点 E,F在AC上,且AE=CF.求证:四边形BEDF是平行四边形.
5. 如图,在 AMCN 中,对角线 AC,MN 交于点O,点 B 和点 D分别在OM,ON 的延长线上.添加以下条件,不能说明四边形ABCD是平行四边形的是( ).
A. AB=AD B. AD∥BC
C. BM=DN D. ∠MAB=∠NCD
6.(2024·贵州遵义二模)如图,佳佳将两个全等的直角三角板(含30°)的直角边重合拼成如图(1)、图(2)的四边形ABCD.
(1)判断四边形 ABCD 的形状为 ;
(2)连接AC,若直角三角板斜边的长为12,请从图(1)、图(2)中选择一个图形,求对角线AC
的长度.
7.(2023·广安中考)如图,在四边形ABCD 中,AC与BD交于点O,BE⊥AC,DF⊥AC,垂足分别为E,F,且AF=CE,∠BAC=∠DCA. 求证:四边形ABCD 是平行四边形.
8.如图,已知E,F 分别是 ABCD 的边 BC,AD上的点,且BE=DF.
(1)求证:四边形 AECF 是平行四边形;
(2)在△ABC 中,若AB=6,AC=8,∠BAC=90°,求 BC边上的高AG.
9.(2024·浙江绍兴柯桥区期末)已知△ABC 和△ADE均为等边三角形,点 F,D 分别在AC,BC上,AF=CD,连接BF,EF.求证:
(1)AD=BF;
(2)四边形 BFED 为平行四边形.
10.中考新考法 动点问题 如图,在四边形ABCD 中,AD∥BC,AD=12cm,BC=15 cm,点 P 自点A 向点D 以1cm/s的速度运动,到 D 点即停止.点 Q 自点C 向B 以2cm/s的速度运动,到B 点即停止,点P,Q同时出发,设运动时间为t(s).
(1)用含 t 的代数式表示:AP = ;DP= ;BQ= ;CQ= .
(2)当t 为何值时,四边形APQB 是平行四边形
(3)当t 为何值时,四边形 PDCQ 是平行四边形
11.(2024·吉安青原区一模)[课本再现]
在学行四边形的概念后,进一步得到平行四边形的性质:平行四边形的对角线互相平分.
(1)如图(1),在平行四边形 ABCD 中,对角线AC 与BD 交于点O,求证:OA=OC,OB=OD.
[知识应用]
(2)在△ABC 中,点 P 为 BC 的中点.延长AB 到D,使得BD=AC,延长AC到E,使得CE=AB,连接DE.如图(2),连接 BE,若∠BAC=60°,请你探究线段 BE 与线段AP之间的数量关系.写出你的结论,并加以证明.
12. 如图,在 ABCD 中,点 E,F 分别在边 BC,AD上,AF=CE.
(1)求证:△ABE≌△CDF;
(2)连接EF.请添加一个与线段相关的条件,使四边形 ABEF 是平行四边形.(不需要说明理由)
13.如图,在四边形ABCD 中,AB∥CD,点E 在边AB上, .请从“①∠B=∠AED;②AE=BE,AE=CD”这两组条件中任选一组作为已知条件,填在横线上(填序号),再解决下列问题:
(1)求证:四边形 BCDE 为平行四边形;
(2)若AD⊥AB,AD=8,BC=10,求线段AE的长.
第2课时 平行四边形(2)
1. D [解析]选项 A符合“两组对边分别平行的四边形是平行四边形”的判定定理,故它能判断这个四边形是平行四边形,不符合题意;选项 B符合“两组对边分别相等的四边形是平行四边形”的判定定理,故它能判断这个四边形是平行四边形,不符合题意;选项C符合“对角线互相平分的四边形是平行四边形”的判定定理,故它能判断这个四边形是平行四边形,不符合题意;因为一组对边平行,另一组对边相等,可能是等腰梯形,所以选项D不能判断这个四边形是平行四边形,符合题意.故选 D.
2. B [解析]把原式变形为 ∵(a-c) ≥0,√b-d≥0,∴a-c=0,b-d=0,∴a=c,b=d,∴该四边形为平行四边形.故选 B.
3.答案不唯一,已知条件可选①③或①④或②④或③④均可.
选择①③:已知:在四边形ABCD中,①AD∥BC,③∠A=∠C.
求证:四边形 ABCD 是平行四边形.
证明:∵AD∥BC,∴∠A+∠B=180°.
∵∠A=∠C,∴∠B+∠C=180°,
∴AB∥CD,∴四边形ABCD 是平行四边形.
选择①④:
已知:在四边形 ABCD 中,①AD∥BC,④∠B+∠C=180°.
求证:四边形 ABCD 是平行四边形.
证明:∵∠B+∠C=180°,∴AB∥CD.又AD∥BC,∴四边形ABCD 是平行四边形.
选择②④:已知:在四边形ABCD中,②AB=CD,④∠B+∠C=180°.
求证:四边形ABCD 是平行四边形.
证明:∵∠B+∠C=180°,∴AB∥CD.
又AB=CD,∴四边形ABCD 是平行四边形.
选择③④:已知:在四边形ABCD 中,③∠A=∠C,④∠B+∠C=180°.
求证:四边形ABCD 是平行四边形.
证明:∵∠B+∠C=180°,∴AB∥CD.
∵∠A=∠C,∴∠A+∠B=180°,∴AD∥BC,
∴四边形ABCD 是平行四边形.
4.如图,连接 BD,与 AC 交于点O.
∵四边形 ABCD 是平行四边形,
∴OA=OC,OB=OD.
∵AE=CF,∴OA-AE=OC-CF,
∴OE=OF,∴四边形BEDF 是平行四边形.
5. A [解析]在□AMCN中,AO=OC,OM=ON.
A.添加AB=AD,不能说明四边形ABCD 是平行四边形,故符合题意;
B.∵AD∥BC,∴∠ADB=∠CBD.
∵AO=CO,∠AOD=∠COB,
∴△AOD≌△COB(AAS),∴OB=OD,
∴四边形 ABCD 是平行四边形,故B 不符合题意;
C.∵BM=DN,∴BM+OM=ON+DN,即OB=OD.∵AO=CO,
∴四边形 ABCD 是平行四边形,故C 不符合题意;
D.∵四边形AMCN 是平行四边形,
∴AM=CN,AM∥CN,∴∠AMO=∠CNO,
∴∠AMB=∠CND.
∵∠BAM=∠DCN,∴△ABM≌△CDN(ASA).
∴AB=CD,∠ABM=∠CDN,∴AB∥CD,
∴四边形ABCD 是平行四边形.故D不符合题意.故选A.
6.(1)平行四边形
(2)选择题图(1),连接AC,设AC和BD 交于点O.
∵∠CBD=30°,∠CDB=90°,BC=12,
∵四边形ABCD 是平行四边形,
7.∵BE⊥AC,DF⊥AC,∴∠AEB=∠DFC=90°.
∵AF=CE,∴AF--EF=CE--EF,∴AE=CF.
在△ABE 与△CDF 中,
∴△ABE≌△CDF(ASA),∴AB=CD.
∵∠BAC=∠DCA,∴AB∥CD,
∴四边形ABCD 是平行四边形.
8.(1)∵四边形ABCD 是平行四边形,
∴AD∥BC,且AD=BC,∴AF∥EC.
∵BE=DF,∴AD-DF=BC--BE,
即AF=EC,∴四边形AECF 是平行四边形.
(2)∵AB=6,AC=8,∠BAC=90°,
∵AG是BC 边上的高,
即 BC 边上的高AG 为
归纳总结本题考查了平行四边形的判定与性质、勾股定理以及三角形面积等知识,熟练掌握平行四边形的判定与性质和勾股定理是解题的关键.
9.(1)∵△ABC为等边三角形,
∴AB=AC,∠BAF=∠C=60°.
∵AF=CD,∴△ABF≌△CAD(SAS),
∴∠ABF=∠CAD,AD=BF.
(2)如图,设AC与DE 相交于点 H,由(1)知,BF=AD.
∵△ADE 是等边三角形,∴AD=DE,
∴BF=DE.
∵∠C=∠AED=60°,∠DHC=∠AHE,
∴∠CDH=∠CAE.
∵∠CAE+∠DAC=∠CBF+∠ABF=60°,∠ABF=∠DAC,
∴∠CBF=∠CAE,∴∠CBF=∠CDH,∴BF∥DE,
∴四边形 BFED 为平行四边形.
■归纳总结 本题考查了平行四边形的判定、等边三角形的性质、全等三角形的判定与性质.灵活运用平行四边形的判定、等边三角形的性质、全等三角形的判定与性质是解题的关键.
10.(1)t cm (12-t) cm (15-2t) cm 2t cm
(2)∵AD∥BC,∴当AP=BQ时,四边形APQB 是平行四边形,∴t=15-2t,解得t=5,
∴当t=5时,四边形APQB 是平行四边形.
(3)∵AD∥BC,即PD∥CQ,
∴当 PD=QC 时,四边形 PDCQ 是平行四边形,即12-t=2t,解得t=4,
∴当t=4时,四边形 PDCQ 是平行四边形.
11.(1)∵四边形ABCD 是平行四边形,
∴AD=BC,AD∥BC,
∴∠OAD=∠OCB,∠ODA=∠OBC,
∴△OAD≌△OCB(ASA),∴OA=OC,OB=OD.
(2)BE=2AP,证明如下:如图所示,过点 B 作 BH∥AE交DE 于点 H,连接PH,CH,
∴∠DBH=∠BAC=60°.
∵AB=CE,AC=BD,
∴AB+BD=AC+CE,即AD=AE,
∴△ADE 是等边三角形,∴∠D=60°,DE=DA,
∴△DBH 是等边三角形,
∴BH=BD=DH,∴BH=AC.
∵BH∥AC,
∴四边形ABHC是平行四边形,
∴AH,BC 互相平分.∵点 P 为BC 的中点,
∴A,P,H 三点共线,∴AH=2AP,
在△ADH 和△EDB 中,
∴△ADH≌△EDB(SAS),
∴BE=AH,∴BE=2AP.
■解后反思 本题考查了平行四边形的性质与判定、全等三角形的性质与判定、等边三角形的性质与判定等,关键是平行四边形判定定理的应用.
12.(1)∵四边形 ABCD 是平行四边形,
∴AB=CD,AD=BC,∠B=∠D.
∵AF=CE,∴AD-AF=BC-CE,
∴DF=BE.
在△ABE与△CDF中,
∴△ABE≌△CDF(SAS).
(2)添加 BE=CE(答案不唯一).理由如下:如图,∵AF=CE,BE=CE,∴AF=BE.
∵四边形ABCD 是平行四边形,
∴AD∥BC,∴AF∥BE,
∴四边形 ABEF 是平行四边形.
■ 易错警示 本题考查了平行四边形的判定与性质以及全等三角形的判定与性质等知识,熟练掌握平行四边形的判定与性质是解题的关键.注意第(2)题添加的条件不唯一.
13.(1)选择①,∵∠B=∠AED,∴BC∥DE.
∵AB∥CD,∴四边形BCDE 为平行四边形.
选择②,∵AE=BE,AE=CD,∴BE=CD,
∵AB∥CD,∴四边形BCDE 为平行四边形.
(2)由(1)可知,四边形 BCDE 为平行四边形,
∴DE=BC=10.∵AD⊥AB,∴∠A=90°,
即线段AE 的长为6.
