19.3.1矩形的性质提优训练 (含答案)
文档属性
| 名称 | 19.3.1矩形的性质提优训练 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 190.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-15 12:54:07 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
19.3.1矩形的性质
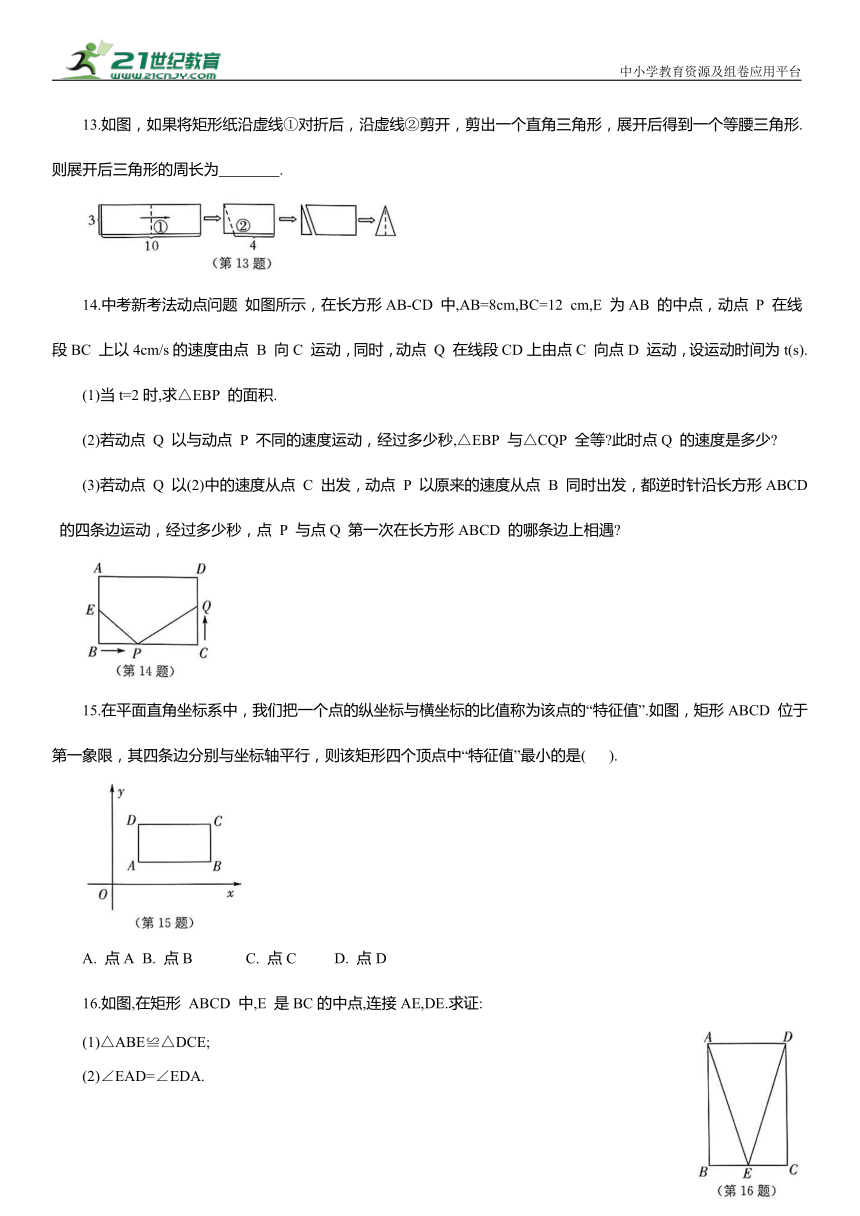
1.如图,将四根木条用钉子钉成一个矩形框架ABCD,然后向左扭动框架,观察所得四边形的变化,下面判断错误的是( ).
A.四边形 ABCD 由矩形变为平行四边形
B.对角线 BD的长度减小
C. 四边形ABCD 的面积不变
D.四边形 ABCD 的周长不变
2.如图,在矩形ABCD 中,对角线 AC 与 BD 相交于点O,则下列结论一定正确的是( ).
A. AB=AD B. AC⊥BD
C. AC=BD D. ∠ACB=∠ACD
3. 矩形的两条对角线的夹角为60°,一条对角线长为2,则矩形的面积为 .
4.如图,在△ABC 中,∠ACB=90°,∠A =54°,D 是AB 的中点,则∠BCD= °.
5.如图,点P 为矩形ABCD 的边AD 上的中点,连接 PB,PC,点E,F 分别在PB,PC 上,且 PE=PF.过点 E作EH∥PC交BC于点 H.求证:四边形CHEF 为平行四边形.
6.如图,矩形ABCD 的对角线AC,BD 相交于点O,AE⊥BD 于点E,∠ADB=35°,则∠OAE 的度数为( ).
A. 20° B. 25° C. 30° D. 35°
如图,在平面直角坐标系xOy中,点A 的坐标为(9,0),点C 的坐标为(0,3),以OA,OC 为边作矩形OABC.动点E,F 分别从点O,B 同时出发,以每秒1个单位长度的速度沿OA,BC向终点A,C移动,当移动时间为4秒时,AC·EF 的值为 .
8.如图,在矩形 ABCD 中,BF∥DE,若AD=12cm,AB=7 cm,且 AE : EB=5 : 2,则S四边形EBFD= .
9.出入相补原理是我国古代数学的重要成就之一,最早是由三国时期数学家刘徽创建.“将一个几何图形,任意切成多块小图形,几何图形的总面积保持不变,等于所分割成的小图形的面积之和”是该原理的重要内容之一.如图,在矩形ABCD 中,AB=5,AD=12,对角线 AC 与BD 交于点O,点 E 为BC 边上的一个动点,EF⊥AC,EG⊥BD,垂足分别为 F,G,则EF+EG= .
10.(2024·浙江湖州期末)如图,在矩形 ABCD 中,∠BAD 的平分线交BC 于点E,F,G 分别是AE 和AD 的中点.
(1)求证:△ABE 是等腰直角三角形;
(2)若AD=4,AB=3,求 FG 的长.
11.如图,将矩形纸片ABCD 沿对角线AC折叠,使点 B 落在点E 处,AE 交CD 于点F,且已知AB=8,BC=4.
(1)判断△ACF 的形状,并说明理由.
(2)求△ACF 的面积.
(3)点 P 为AC 上一动点,则PE+PF 最小值为多少
12.如图,在矩形OABC 中,O 为直角坐标系的原点,A,C 两点的坐标分别为(6,0),(0,10),点 B 在第一象限内.
(1)写出点 B 的坐标,并求矩形OABC 的周长;
(2)若有过点 C 的直线CD 把矩形OABC 的周长分成3:5两部分,D为直线CD 与矩形的边的交点,求点 D 的坐标.
13.如图,如果将矩形纸沿虚线①对折后,沿虚线②剪开,剪出一个直角三角形,展开后得到一个等腰三角形.则展开后三角形的周长为 .
14.中考新考法动点问题 如图所示,在长方形AB-CD 中,AB=8cm,BC=12 cm,E 为AB 的中点,动点 P 在线段BC 上以4cm/s的速度由点 B 向C 运动,同时,动点 Q 在线段CD上由点C 向点D 运动,设运动时间为t(s).
(1)当t=2时,求△EBP 的面积.
(2)若动点 Q 以与动点 P 不同的速度运动,经过多少秒,△EBP 与△CQP 全等 此时点Q 的速度是多少
(3)若动点 Q 以(2)中的速度从点 C 出发,动点 P 以原来的速度从点 B 同时出发,都逆时针沿长方形ABCD 的四条边运动,经过多少秒,点 P 与点Q 第一次在长方形ABCD 的哪条边上相遇
15.在平面直角坐标系中,我们把一个点的纵坐标与横坐标的比值称为该点的“特征值”.如图,矩形ABCD 位于第一象限,其四条边分别与坐标轴平行,则该矩形四个顶点中“特征值”最小的是( ).
A. 点A B. 点B C. 点C D. 点D
16.如图,在矩形 ABCD 中,E 是BC的中点,连接AE,DE.求证:
(1)△ABE≌△DCE;
(2)∠EAD=∠EDA.
1. C [解析]向左扭动矩形框架ABCD,只改变四边形的形状,四边形变成平行四边形,A不符合题意;此时对角线 BD 减小,对角线AC增大,B不符合题意;BC边上的高减小,故面积变小,C符合题意;四边形的四条边不变,故周长不变,D不符合题意.故选 C.
2. C [解析]矩形的对边平行且相等,矩形的四个角都是直角,矩形的对角线相等,因此选项C一定正确.故选C.
3. [解析]如图,矩形的两条对角线的夹角为
∵矩形对角线相等且互相平
分,∴△AOB为等边三角形,
在Rt△ABC中,AC=2,AB=1,
故矩形的面积为
4.36 [解析]∵在△ABC中,∠ACB=90°,∠A=54°,D是AB的中点,
∴∠B=36°,BD=CD,∴∠BCD=36°.
5.∵点P 为矩形ABCD的边AD的中点,∴PA=PD,四边形ABCD是矩形,∴∠A=∠D=90°,AB=DC,
∴△APB≌△DPC(SAS),
∴PB=PC,∴∠PBC=∠PCB.
∵PE=PF,∴∠PEF=∠PFE.
∵∠EPF=∠BPC,
∴∠PEF=∠PBC,∴EF∥BC.
∵EH∥FC,∴四边形CHEF 为平行四边形.
归纳总结 本题考查的是全等三角形的判定与性质、等腰三角形的性质、矩形的性质、平行四边形的判定,掌握以上知识是解本题的关键.
6. A [解析]∵矩形对角线相等且互相平分,
∴∠OAD=∠ODA=35°,∴∠AOE=2∠ADB=70°,
.故选 A.
7.30 [解析]如图,连接AC,EF.
∵点A 的坐标为(9,0),点C的坐标为(0,3),四边形OABC 是以OA,OC为边作矩形OABC,
∴OA=BC=9,OC=AB=3,
当移动时间为4秒时,得OE=4×1=4,BF=4×1=4,∴AE=9-4=5,则E(4,0),
∴CF=BC-BF=9-4=5,∴F(5,3),
■ 思路引导 本题考查了坐标与图形、勾股定理求两点距离、矩形的性质,求出 E,F的坐标是解题的关键.
8.24cm [解析]由矩形性质可知AD⊥AB,即AD为四边形EBFD 的高.∵BE∥DF,BF∥DE,∴四边形EBFD是平行四边形.∵AE:EB=5:2,AB=7cm,∴BE=2cm,∴S四边形EBFD=2×12=24(cm ).
9. [解析]如图,连接OE.
∵四边形ABCD 是矩形,∴∠ABC=90°,BC=AD=12,AO=CO=BO=DO.
12=15,
素养考向 本题考查了矩形的性质、勾股定理.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.
10.(1)∵AE平分∠BAD,∴∠BAE=∠DAE.在矩形ABCD中,∠B=90°,AD∥BC,
∴∠DAE=∠AEB,
∴∠BAE=∠AEB,
∴AB=BE,即△ABE 是等腰直角三角形.
(2)由(1),得BE=AB=3.
在矩形ABCD中,BC=AD=4,DC=AB=3,∴EC=BC-BE=1.
如图,连接DE.
在Rt△DCE中,
∵F,G分别为AE与AD的中点,
归纳总结 本题考查矩形的性质、角平分线的性质、勾股定理、三角形中位线定理,解题的关键是掌握相关知识并灵活运用.
11.(1)△ACF 是等腰三角形.理由如下:如图(1),由折叠可知∠1=∠2.
∵四边形ABCD 是矩形,
∴AB∥CD,∴∠2=∠3,
∴∠1=∠3,∴AF=CF,
∴△ACF 是等腰三角形.
(2)∵四边形ABCD 是矩形且AB=8,BC=4,
∴AD=BC=4,CD=AB=8,∠D=90°.
设FD=x,则AF=CF=8-x,
在 Rt△AFD 中,根据勾股定理,得 解得x=3,即DF=3,
∴CF=8-3=5,
(3)如图(2),在AC上任取一点 P,连接PB,PE,PF.由折叠,得点 B,E 关于AC对称,∴PE=PB,
∴PE+PF=PF+PB,
∴当点 F,P,B 三点共线时,PE+PF 最小,最小值为 BF的长.
由(2)知CF=5,
∵BC=4,∠BCF=90°,
即PE+PF 最小值为
12.(1)∵A(6,0),C(0,10),∴OA=6,OC=10.
∵四边形OABC 是矩形,
∴BC=OA=6,AB=OC=10,
∴点 B 的坐标为(6,10).
∵OC=10,OA=6,
∴矩形OABC的周长为2×(6+10)=32.
(2)∵CD 把长方形OABC的周长分为3:5两部分,
∴被分成的两部分的长分别为12 和20.
①当点 D 在AB上时,AD=20-10-6=4,
∴点 D 的坐标为(6,4);
②当点 D 在OA 上时,OD=12-10=2,∴点 D 的坐标为(2,0).
综上所述,点 D 的坐标为(6,4)或(2,0).
[解析]由题意可知剪出的一个直角三角形的竖直方向直角边长为3,水平方向直角边长为 从而展开后得到的等腰三角形底边长为2×1=2,再由勾股定理求出腰长 所以周长为
14.(1)当t=2时,BP=2×4=8(cm).
∵E为AB 的中点,
(2)设点 Q 的速度是a cm/s,则BP=4t cm,CQ=at cm,∴PC=(12-4t) cm.
∵△EBP 与△CQP 中,∠B=∠C=90°,
∴△EBP≌△PCQ 或△EBP≌△QCP.
当△EBP≌△PCQ时,PC=EB,CQ=BP,
∴12-4t=4,解得t=2,∴2a=4×2,
∴a=4,与动点Q 以与动点P 不同的速度运动矛盾(舍去);
当△EBP≌△QCP 时,CP=BP,CQ=BE,∴12-4t=4t,解得 解得
故经过 s,△EBP≌△QCP,此时点 Q 的速度是
(3)设经过x秒,点 P 与点 Q第一次在长方形 ABCD的边上相遇,则 解得x=9.
此时点 P 运动路程为4×9=36(cm),
∴点 P 在AB 的中点处.
故经过9秒,点 P 与点 Q 第一次在长方形ABCD的边AB上相遇.
素养考向 本题运用矩形性质、全等三角形判定和性质、分类讨论思想等知识,通过推理与计算,解决所求,考查推理能力和运算能力的核心素养.
15. B [解析]设A(a,b),AB=m,AD=n.
∵四边形ABCD 是矩形,
∴AD=BC=n,AB=CD=m,
∴D(a,b+n),B(a+m,b),C(a+m,b+n).
而
∴该矩形四个顶点中“特征值”最小的是点 B.故选B.
—思路引导 本题考查了矩形的性质、坐标与图形的性质,解答本题的关键是结合新定义与分式的值的大小比较,从而得到四个点中“特征值”最小的一个.
16.(1)∵四边形ABCD 是矩形,
∴AB=DC,∠B=∠C=90°.
∵E是BC的中点,∴BE=CE.
在△ABE 和△DCE 中.
∴△ABE≌△DCE(SAS).
(2)∵△ABE≌△DCE,
∴AE=DE,∴∠EAD=∠EDA.
解后反思本题考查了矩形的性质,全等三角形的判定和性质,等边对等角,解题的关键是掌握相关知识并能灵活运用.
19.3.1矩形的性质
1.如图,将四根木条用钉子钉成一个矩形框架ABCD,然后向左扭动框架,观察所得四边形的变化,下面判断错误的是( ).
A.四边形 ABCD 由矩形变为平行四边形
B.对角线 BD的长度减小
C. 四边形ABCD 的面积不变
D.四边形 ABCD 的周长不变
2.如图,在矩形ABCD 中,对角线 AC 与 BD 相交于点O,则下列结论一定正确的是( ).
A. AB=AD B. AC⊥BD
C. AC=BD D. ∠ACB=∠ACD
3. 矩形的两条对角线的夹角为60°,一条对角线长为2,则矩形的面积为 .
4.如图,在△ABC 中,∠ACB=90°,∠A =54°,D 是AB 的中点,则∠BCD= °.
5.如图,点P 为矩形ABCD 的边AD 上的中点,连接 PB,PC,点E,F 分别在PB,PC 上,且 PE=PF.过点 E作EH∥PC交BC于点 H.求证:四边形CHEF 为平行四边形.
6.如图,矩形ABCD 的对角线AC,BD 相交于点O,AE⊥BD 于点E,∠ADB=35°,则∠OAE 的度数为( ).
A. 20° B. 25° C. 30° D. 35°
如图,在平面直角坐标系xOy中,点A 的坐标为(9,0),点C 的坐标为(0,3),以OA,OC 为边作矩形OABC.动点E,F 分别从点O,B 同时出发,以每秒1个单位长度的速度沿OA,BC向终点A,C移动,当移动时间为4秒时,AC·EF 的值为 .
8.如图,在矩形 ABCD 中,BF∥DE,若AD=12cm,AB=7 cm,且 AE : EB=5 : 2,则S四边形EBFD= .
9.出入相补原理是我国古代数学的重要成就之一,最早是由三国时期数学家刘徽创建.“将一个几何图形,任意切成多块小图形,几何图形的总面积保持不变,等于所分割成的小图形的面积之和”是该原理的重要内容之一.如图,在矩形ABCD 中,AB=5,AD=12,对角线 AC 与BD 交于点O,点 E 为BC 边上的一个动点,EF⊥AC,EG⊥BD,垂足分别为 F,G,则EF+EG= .
10.(2024·浙江湖州期末)如图,在矩形 ABCD 中,∠BAD 的平分线交BC 于点E,F,G 分别是AE 和AD 的中点.
(1)求证:△ABE 是等腰直角三角形;
(2)若AD=4,AB=3,求 FG 的长.
11.如图,将矩形纸片ABCD 沿对角线AC折叠,使点 B 落在点E 处,AE 交CD 于点F,且已知AB=8,BC=4.
(1)判断△ACF 的形状,并说明理由.
(2)求△ACF 的面积.
(3)点 P 为AC 上一动点,则PE+PF 最小值为多少
12.如图,在矩形OABC 中,O 为直角坐标系的原点,A,C 两点的坐标分别为(6,0),(0,10),点 B 在第一象限内.
(1)写出点 B 的坐标,并求矩形OABC 的周长;
(2)若有过点 C 的直线CD 把矩形OABC 的周长分成3:5两部分,D为直线CD 与矩形的边的交点,求点 D 的坐标.
13.如图,如果将矩形纸沿虚线①对折后,沿虚线②剪开,剪出一个直角三角形,展开后得到一个等腰三角形.则展开后三角形的周长为 .
14.中考新考法动点问题 如图所示,在长方形AB-CD 中,AB=8cm,BC=12 cm,E 为AB 的中点,动点 P 在线段BC 上以4cm/s的速度由点 B 向C 运动,同时,动点 Q 在线段CD上由点C 向点D 运动,设运动时间为t(s).
(1)当t=2时,求△EBP 的面积.
(2)若动点 Q 以与动点 P 不同的速度运动,经过多少秒,△EBP 与△CQP 全等 此时点Q 的速度是多少
(3)若动点 Q 以(2)中的速度从点 C 出发,动点 P 以原来的速度从点 B 同时出发,都逆时针沿长方形ABCD 的四条边运动,经过多少秒,点 P 与点Q 第一次在长方形ABCD 的哪条边上相遇
15.在平面直角坐标系中,我们把一个点的纵坐标与横坐标的比值称为该点的“特征值”.如图,矩形ABCD 位于第一象限,其四条边分别与坐标轴平行,则该矩形四个顶点中“特征值”最小的是( ).
A. 点A B. 点B C. 点C D. 点D
16.如图,在矩形 ABCD 中,E 是BC的中点,连接AE,DE.求证:
(1)△ABE≌△DCE;
(2)∠EAD=∠EDA.
1. C [解析]向左扭动矩形框架ABCD,只改变四边形的形状,四边形变成平行四边形,A不符合题意;此时对角线 BD 减小,对角线AC增大,B不符合题意;BC边上的高减小,故面积变小,C符合题意;四边形的四条边不变,故周长不变,D不符合题意.故选 C.
2. C [解析]矩形的对边平行且相等,矩形的四个角都是直角,矩形的对角线相等,因此选项C一定正确.故选C.
3. [解析]如图,矩形的两条对角线的夹角为
∵矩形对角线相等且互相平
分,∴△AOB为等边三角形,
在Rt△ABC中,AC=2,AB=1,
故矩形的面积为
4.36 [解析]∵在△ABC中,∠ACB=90°,∠A=54°,D是AB的中点,
∴∠B=36°,BD=CD,∴∠BCD=36°.
5.∵点P 为矩形ABCD的边AD的中点,∴PA=PD,四边形ABCD是矩形,∴∠A=∠D=90°,AB=DC,
∴△APB≌△DPC(SAS),
∴PB=PC,∴∠PBC=∠PCB.
∵PE=PF,∴∠PEF=∠PFE.
∵∠EPF=∠BPC,
∴∠PEF=∠PBC,∴EF∥BC.
∵EH∥FC,∴四边形CHEF 为平行四边形.
归纳总结 本题考查的是全等三角形的判定与性质、等腰三角形的性质、矩形的性质、平行四边形的判定,掌握以上知识是解本题的关键.
6. A [解析]∵矩形对角线相等且互相平分,
∴∠OAD=∠ODA=35°,∴∠AOE=2∠ADB=70°,
.故选 A.
7.30 [解析]如图,连接AC,EF.
∵点A 的坐标为(9,0),点C的坐标为(0,3),四边形OABC 是以OA,OC为边作矩形OABC,
∴OA=BC=9,OC=AB=3,
当移动时间为4秒时,得OE=4×1=4,BF=4×1=4,∴AE=9-4=5,则E(4,0),
∴CF=BC-BF=9-4=5,∴F(5,3),
■ 思路引导 本题考查了坐标与图形、勾股定理求两点距离、矩形的性质,求出 E,F的坐标是解题的关键.
8.24cm [解析]由矩形性质可知AD⊥AB,即AD为四边形EBFD 的高.∵BE∥DF,BF∥DE,∴四边形EBFD是平行四边形.∵AE:EB=5:2,AB=7cm,∴BE=2cm,∴S四边形EBFD=2×12=24(cm ).
9. [解析]如图,连接OE.
∵四边形ABCD 是矩形,∴∠ABC=90°,BC=AD=12,AO=CO=BO=DO.
12=15,
素养考向 本题考查了矩形的性质、勾股定理.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.
10.(1)∵AE平分∠BAD,∴∠BAE=∠DAE.在矩形ABCD中,∠B=90°,AD∥BC,
∴∠DAE=∠AEB,
∴∠BAE=∠AEB,
∴AB=BE,即△ABE 是等腰直角三角形.
(2)由(1),得BE=AB=3.
在矩形ABCD中,BC=AD=4,DC=AB=3,∴EC=BC-BE=1.
如图,连接DE.
在Rt△DCE中,
∵F,G分别为AE与AD的中点,
归纳总结 本题考查矩形的性质、角平分线的性质、勾股定理、三角形中位线定理,解题的关键是掌握相关知识并灵活运用.
11.(1)△ACF 是等腰三角形.理由如下:如图(1),由折叠可知∠1=∠2.
∵四边形ABCD 是矩形,
∴AB∥CD,∴∠2=∠3,
∴∠1=∠3,∴AF=CF,
∴△ACF 是等腰三角形.
(2)∵四边形ABCD 是矩形且AB=8,BC=4,
∴AD=BC=4,CD=AB=8,∠D=90°.
设FD=x,则AF=CF=8-x,
在 Rt△AFD 中,根据勾股定理,得 解得x=3,即DF=3,
∴CF=8-3=5,
(3)如图(2),在AC上任取一点 P,连接PB,PE,PF.由折叠,得点 B,E 关于AC对称,∴PE=PB,
∴PE+PF=PF+PB,
∴当点 F,P,B 三点共线时,PE+PF 最小,最小值为 BF的长.
由(2)知CF=5,
∵BC=4,∠BCF=90°,
即PE+PF 最小值为
12.(1)∵A(6,0),C(0,10),∴OA=6,OC=10.
∵四边形OABC 是矩形,
∴BC=OA=6,AB=OC=10,
∴点 B 的坐标为(6,10).
∵OC=10,OA=6,
∴矩形OABC的周长为2×(6+10)=32.
(2)∵CD 把长方形OABC的周长分为3:5两部分,
∴被分成的两部分的长分别为12 和20.
①当点 D 在AB上时,AD=20-10-6=4,
∴点 D 的坐标为(6,4);
②当点 D 在OA 上时,OD=12-10=2,∴点 D 的坐标为(2,0).
综上所述,点 D 的坐标为(6,4)或(2,0).
[解析]由题意可知剪出的一个直角三角形的竖直方向直角边长为3,水平方向直角边长为 从而展开后得到的等腰三角形底边长为2×1=2,再由勾股定理求出腰长 所以周长为
14.(1)当t=2时,BP=2×4=8(cm).
∵E为AB 的中点,
(2)设点 Q 的速度是a cm/s,则BP=4t cm,CQ=at cm,∴PC=(12-4t) cm.
∵△EBP 与△CQP 中,∠B=∠C=90°,
∴△EBP≌△PCQ 或△EBP≌△QCP.
当△EBP≌△PCQ时,PC=EB,CQ=BP,
∴12-4t=4,解得t=2,∴2a=4×2,
∴a=4,与动点Q 以与动点P 不同的速度运动矛盾(舍去);
当△EBP≌△QCP 时,CP=BP,CQ=BE,∴12-4t=4t,解得 解得
故经过 s,△EBP≌△QCP,此时点 Q 的速度是
(3)设经过x秒,点 P 与点 Q第一次在长方形 ABCD的边上相遇,则 解得x=9.
此时点 P 运动路程为4×9=36(cm),
∴点 P 在AB 的中点处.
故经过9秒,点 P 与点 Q 第一次在长方形ABCD的边AB上相遇.
素养考向 本题运用矩形性质、全等三角形判定和性质、分类讨论思想等知识,通过推理与计算,解决所求,考查推理能力和运算能力的核心素养.
15. B [解析]设A(a,b),AB=m,AD=n.
∵四边形ABCD 是矩形,
∴AD=BC=n,AB=CD=m,
∴D(a,b+n),B(a+m,b),C(a+m,b+n).
而
∴该矩形四个顶点中“特征值”最小的是点 B.故选B.
—思路引导 本题考查了矩形的性质、坐标与图形的性质,解答本题的关键是结合新定义与分式的值的大小比较,从而得到四个点中“特征值”最小的一个.
16.(1)∵四边形ABCD 是矩形,
∴AB=DC,∠B=∠C=90°.
∵E是BC的中点,∴BE=CE.
在△ABE 和△DCE 中.
∴△ABE≌△DCE(SAS).
(2)∵△ABE≌△DCE,
∴AE=DE,∴∠EAD=∠EDA.
解后反思本题考查了矩形的性质,全等三角形的判定和性质,等边对等角,解题的关键是掌握相关知识并能灵活运用.
