一元二次方程的解法与应用期末专题整合提优(二) (含答案)
文档属性
| 名称 | 一元二次方程的解法与应用期末专题整合提优(二) (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 115.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-16 05:58:02 | ||
图片预览



文档简介
一元二次方程的解法与应用期末专题整合提优(二)
中小学教育资源及组卷应用平台
一、选择题
1.(2024·山东烟台经开区期末)一元二次方程(x+ 用直接开平方法可转化为两个一元一次方程,其中一个一元一次方程是x+1=4,则另一个一元一次方程是( ).
A. x---1=-4 B. x---1=4
C. x+1=-4 D. x+1=4
2.若关于x 的一元二次方程 的常数项为0,则m 的值等于( ).
A. 1 B. 2 C. 1或2 D. 0
3.用配方法解方程 时,配方后得到的方程是( ).
4.方程 根的符号是( ).
A. 两根一正一负 B.两根都是负数
C. 两根都是正数 D.无法确定
5.(2024·福建福州鼓楼区联考期末)某校“玩转数学”活动小组在一次实践调查中发现某种植物的1个主干上长出x个枝干,每个枝干上再长出x个小分枝.若在1个主干上的主干、枝干和小分枝的总数是31个,则下列方程中正确的是( ).
6.若长方形的长和宽是方程 的两个根,则长方形的周长和面积分别是( ).
A. 6 和 B. 6和3
C. 12和3 D. 3和
7.一个跳水运动员从10米高台上跳水,他每一时刻所在高度h(单位:米)与所用时间t(单位:秒)的关系是h=-5(t-2)(t+1),则该运动员从起跳到入水所用的时间是( ).
A. 5秒 B. 2秒 C. 3秒 D. 1秒
8.已知三角形的两边长分别是3 和6,第三边的长是一元二次方程 的根,则这个三角形的周长等于( ).
A. 13 B. 11
C. 11或13 D. 12或15
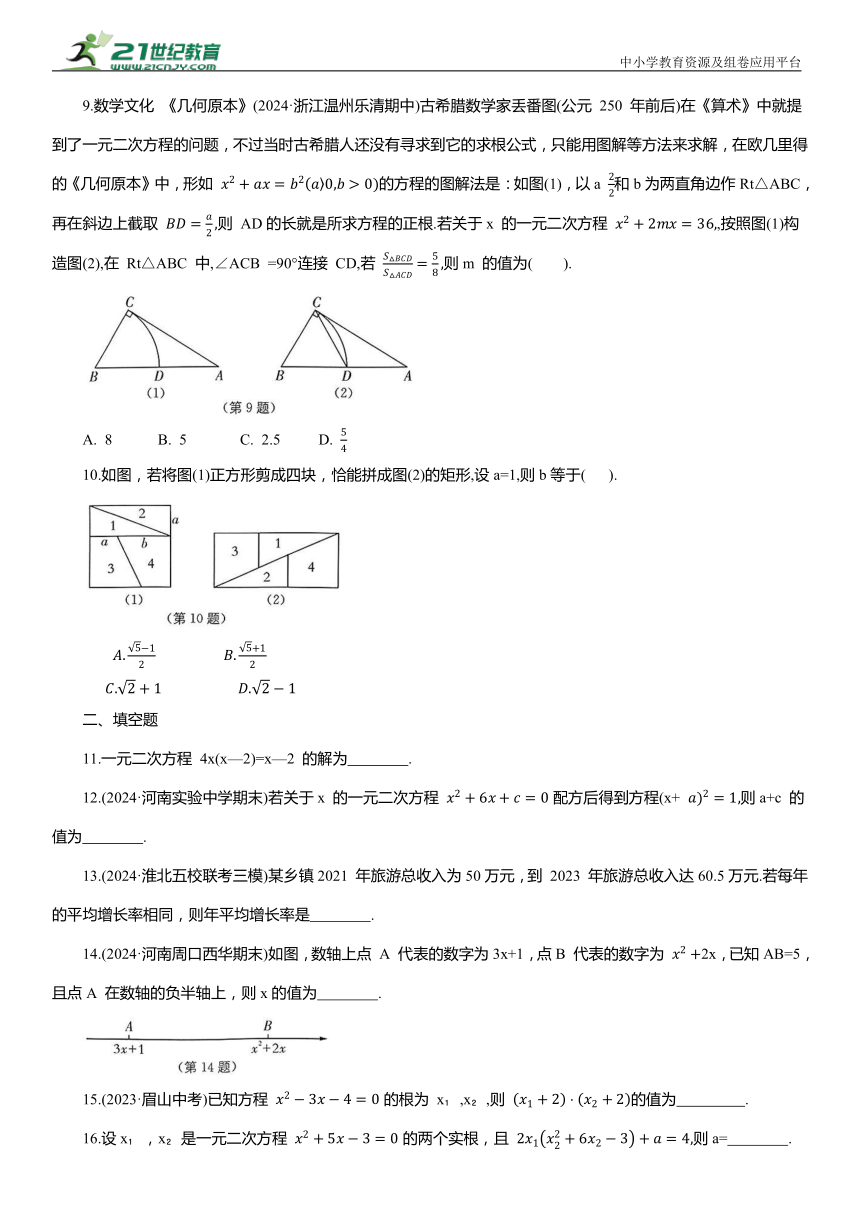
9.数学文化 《几何原本》(2024·浙江温州乐清期中)古希腊数学家丢番图(公元 250 年前后)在《算术》中就提到了一元二次方程的问题,不过当时古希腊人还没有寻求到它的求根公式,只能用图解等方法来求解,在欧几里得的《几何原本》中,形如 的方程的图解法是:如图(1),以a 和b为两直角边作Rt△ABC,再在斜边上截取 则 AD的长就是所求方程的正根.若关于x 的一元二次方程 ,按照图(1)构造图(2),在 Rt△ABC 中,∠ACB =90°连接 CD,若 则m 的值为( ).
A. 8 B. 5 C. 2.5 D.
10.如图,若将图(1)正方形剪成四块,恰能拼成图(2)的矩形,设a=1,则b等于( ).
二、填空题
11.一元二次方程 4x(x—2)=x—2 的解为 .
12.(2024·河南实验中学期末)若关于x 的一元二次方程 配方后得到方程(x+ 则a+c 的值为 .
13.(2024·淮北五校联考三模)某乡镇2021 年旅游总收入为50万元,到 2023 年旅游总收入达60.5万元.若每年的平均增长率相同,则年平均增长率是 .
14.(2024·河南周口西华期末)如图,数轴上点 A 代表的数字为3x+1,点B 代表的数字为 2x,已知AB=5,且点A 在数轴的负半轴上,则x的值为 .
15.(2023·眉山中考)已知方程 的根为 x ,x ,则 的值为 .
16.设x ,x 是一元二次方程 的两个实根,且 则a= .
三、解答题
17.中考新考法 过程纠错改错 阅读材料,并回答问题:
小明在学习一元二次方程时,
解方程 的过程如下:
解:∵a=2,b=--1,c=-3①,
=1-24=-23<0③,
∴此方程无解.
问题:(1)上述过程中,从 步开始出现了错误(填序号);
(2)发生错误的原因是: ;
(3)在下面的空白处,写出正确的解答过程.
18.中考新考法 解题方法型阅读理解题(2024·江苏苏州期中)阅读材料:为解方程 1)=0,我们可以将 视为一个整体,然后设 将原方程化为 解得
当y=0时,
当y=3时,
∴原方程的解为
由原方程得到①的过程,利用换元法达到了简化方程的目的,体现了整体转化的数学思想.
阅读后解答问题:
(1)利用上述材料中的方法解方程:
(2)已知一元二次方程. 的两根分别为--3,1,求方程a(2x+m- 的两根.
19.某平台爆红网络,某电商在该平台上直播带货,已知该产品的进货价为70元/件,为吸引流量,该电商在直播中承诺自家商品价格永远不会超过99元/件,根据一个月的市场调研,商家发现当售价为 110 元/件时,日销售量为20件,售价每降低1元,日销售量增加2件.
(1)当销售量为 30 件时,产品售价为 元/件.
(2)直接写出日销售量y(件)与售价x(元/件)的函数关系式.
(3)该产品的售价每件应定为多少,电商每天可盈利1200元
20.为推进生态文明建设,加快发展新能源汽车,国家对新能源汽车实行补贴政策.一家4S店从事某品牌纯电动汽车和插电式混动汽车两种新能源汽车(以下简称电动车和混动车)的销售,电动车每辆进价16万元,去年国家对该车每辆补贴4.5万元,补贴后每辆售价14万元;混动车每辆进价18万元,去年国家对该车每辆补贴2.8万元,补贴后每辆售价18万元.该4S店去年12月共销售这两种汽车120辆,获得利润324万元.
(1)该4S店去年12月销售了多少辆混动车
(2)今年国家对该品牌新能源汽车的补贴有所下降,电动车每辆比去年少补贴0.5万元,混动车每辆比去年少补贴0.8万元,该4S店为减少损失,今年1月把电动车的售价提高了m%,结果销量在去年12月的基础上减少
了 m%,对混动车的售价没有作调整,而销量在去年12月的基础上增加了2.4m辆,结果该4S店今年1月的利润比去年12月少了14万元,求m的值.
21.新情境设计花园 在一块长16m、宽12m的矩形荒地上建一个花园,要求花园所占面积为荒地面积的一半,图(1)是小明的设计方案,花园四周小路的宽度相等,通过解方程,小明得到小路的宽为2m 或12m.图(2)是小丽的设计方案,其中花园四个角上的扇形都相同.
(1)你认为小明的计算结果对吗 请说明理由.
(2)请你帮小丽求出图中的x.(精确到0.1)
(3)你还有其他的设计方案吗 请在图(3)中画出你设计的草图,并简要说明.
1. C [解析]∵ ∴x+1=4或x+1=-4.故选C.
2. B [解析]由题意,得常数项为0,则 0,(m-1)(m--2)=0,解得 又由一元二次方程概念可得m-1≠0,即m≠1.故m的值等于2.故选 B.
易错警示 本题考查一元二次方程的概念和解法.解答较易出现错误的是直接根据常数项为0解得m的值为1或2,忽略了一元二次方程中m≠1的隐含条件,造成错解.
3. A [解析] 12.故选 A.
4. C [解析]·
∴(2x-1)(x-1)=0,解得
∴方程 的两根都是正数.故选C.
5. C [解析]1个主干上的主干、支干和小分枝的总数是31个,其中枝干有x个,小分枝有x 个,于是可得方程 故选 C.
6. A [解析]设长方形的长等于a,宽等于b,因为长方形的长和宽是方程 的两个根,则 故长方形的周长=2(a+b)=2×3=6,长方形的面积 故选 A.
光速解法 根据题意,直接利用一元二次方程根与系数的关系,得到长方形长和宽的和与积,即可得到长方形的周长与面积.
7. B [解析]设运动员起跳到入水所用的时间是t秒,根据题意可知,-5(t-2)(t+1)=0,解得 -1(不合题意,舍去), 那么该运动员起跳到入水所用的时间是2秒.故选 B.
易错警示 解答本题时,要注意题意给出的是高度与时间的关系式,所以高度代入的是0不是10,故将高度代入所得的方程为-5(t-2)(t+1)=0,不是-5(t-2)(t+1)=10.
8. A [解析]由题意知, 解得
当第三边长是2时,2+3<6,不能构成三角形;
当第三边长是4时,三角形的周长为4+3+6=13.故选 A.
C [解析]∵∠ACB=90°,BC=BD=m,AC=6,
即
解得m=2.5或m=-2.5,根据题意m>0,∴m=2.5;经检验,m=2.5是原方程的解.故选C.
思路引导本题考查一元二次方程的应用,解题的关键是列出方程,难点是解方程: ,去分母,得 移项、合并同类项,得 即 由算术平方根的定义得 解得m=2.5(m>0).
10. B [解析]依题意,得(
又b不能为负, 故选B.
方法诠释本题是一个信息题目,首先正确理解题目的意思,然后根据题目隐含条件找到数量关系,再利用数量关系列出方程解决问题.根据图(1)可以知道图形是一个正方形,边长为(a+b),图(2)是一个长方形,长、宽分别为(b+a+b),b,并且它们的面积相等,由此即可列出等式( 而a=1,代入即可得到关于b的方程,解方程即可求出b.
[解析]移项,得4x(x-2)--(x-2)=0,提公因式,得(4x-1)(x-2)=0,解得.
易错警示 解答此方程时,不能直接根据等式性质将左右两边的(x-2)约去,因为当x--2=0时,左右两边也相等,即x=2时,方程也成立,故x=2是方程的一个根.
12.11 [解析]
移项,得
配方,得
∵方程 配方后得到
∴a=3,9-c=1,∴c=8,∴a+c=3+8=11.
思路引导先把常数项移到等号的另一边,方程的两边都加上一次项系数一半的平方后得新方程,根据题目中两个方程相等确定a,c,最后求出a+c.
13.10% [解析]设年平均增长率是x,利用该乡镇2023年旅游总收入=该乡镇2021年旅游总收入×(1+年平均增长率) ,可列出关于x 的一元二次方程 (不符合题意,舍去),∴年平均增长率是10%.
14.-2 [解析]根据题意,得 整理,得
∴(x-3)(x+2)=0,∴x-3=0或x+2=0,
当x=3时,3x+1=10>0,舍去,∴x的值为-2.
思路引导先利用数轴上两点之间的距离的求法得到 ,再把方程化为一般式为 ,接着利用因式分解法把方程转化为x-3=0或x+2=0,然后解两个一次方程,从而可得到满足条件的x的值.
15.6 [解析]∵方程 的根为x ,x ,
=-4+2×3+4=6.
解后反思 本题考查了一元二次方程根与系数的关系: 直接利用根与系数的关系作答.
16.10 [解析]由于x ,x 是. 的两个实数根, 于是 a-6=4,解得a=10.
17.(1)③
(2)计算结果错误(负数乘负数得负数).
(3)∵a=2,b=-1,c=-3,
18.(1)令 则
∴(m-2)(m+1)=0,∴m-2=0或m+1=0,解得m=2或m=-1.
当m=2时, 即 解得
当m=-1时, 即 解得
综上,原方程的解为
(2)∵一元二次方程 的两根分别为--3,1,
∴方程 中2x-4=-3或2x-4=1,解得 或
即方程 的两根分别是 和
●素养考向 本题主要考查换元法解一元二次方程,考查了模型观念、运算能力的核心素养,熟练掌握换元法和一元二次方程的解法是关键,体现了整体转化的数学思想.
19.(1)105
(2)根据题意,得y=20+2(110-x)=-2x+240.
∵该产品的进货价为70元/件,且该电商在直播中承诺自家商品价格永远不会超过99元/件,∴日销售量y(件)与售价x(元/件)的函数关系式为y=-2x+240(70≤x≤99).
(3)根据题意,得(x-70)(-2x+240)=1200,
整理,得
解得 (不符合题意,舍去).
故该产品的售价每件应定为90元.
20.(1)设该4S店去年12月销售了x辆混动车,则销售了(120-x)辆电动车.
由题意,得(14+4.5-16)(120-x)+(18+2.8-18)x=324,解得x=80.
故该4S店去年12月销售了80辆混动车.
(2)由题意,得[14(1+m%)+4-16]×(120-80)× 14,解得
当m=50时, 不符合题意,舍去.故m的值为10.
21.(1)小明的计算结果不对.理由如下:
设小路宽 ym,根据题意,得(16-2y)(12-2y)= 解得
因为荒地的宽为12m,所以 不符合题意,舍去.故取y=2,所以小路的宽为2m.
(2)由题意,得 所以 解得x≈±5.5.
因为扇形的半径不能为负数,所以取x≈5.5.
(3)如图所示,取四边中点,依次连接各边中点所得的四边形即为所要设计的花园的草图.(答案不唯一)
中小学教育资源及组卷应用平台
一、选择题
1.(2024·山东烟台经开区期末)一元二次方程(x+ 用直接开平方法可转化为两个一元一次方程,其中一个一元一次方程是x+1=4,则另一个一元一次方程是( ).
A. x---1=-4 B. x---1=4
C. x+1=-4 D. x+1=4
2.若关于x 的一元二次方程 的常数项为0,则m 的值等于( ).
A. 1 B. 2 C. 1或2 D. 0
3.用配方法解方程 时,配方后得到的方程是( ).
4.方程 根的符号是( ).
A. 两根一正一负 B.两根都是负数
C. 两根都是正数 D.无法确定
5.(2024·福建福州鼓楼区联考期末)某校“玩转数学”活动小组在一次实践调查中发现某种植物的1个主干上长出x个枝干,每个枝干上再长出x个小分枝.若在1个主干上的主干、枝干和小分枝的总数是31个,则下列方程中正确的是( ).
6.若长方形的长和宽是方程 的两个根,则长方形的周长和面积分别是( ).
A. 6 和 B. 6和3
C. 12和3 D. 3和
7.一个跳水运动员从10米高台上跳水,他每一时刻所在高度h(单位:米)与所用时间t(单位:秒)的关系是h=-5(t-2)(t+1),则该运动员从起跳到入水所用的时间是( ).
A. 5秒 B. 2秒 C. 3秒 D. 1秒
8.已知三角形的两边长分别是3 和6,第三边的长是一元二次方程 的根,则这个三角形的周长等于( ).
A. 13 B. 11
C. 11或13 D. 12或15
9.数学文化 《几何原本》(2024·浙江温州乐清期中)古希腊数学家丢番图(公元 250 年前后)在《算术》中就提到了一元二次方程的问题,不过当时古希腊人还没有寻求到它的求根公式,只能用图解等方法来求解,在欧几里得的《几何原本》中,形如 的方程的图解法是:如图(1),以a 和b为两直角边作Rt△ABC,再在斜边上截取 则 AD的长就是所求方程的正根.若关于x 的一元二次方程 ,按照图(1)构造图(2),在 Rt△ABC 中,∠ACB =90°连接 CD,若 则m 的值为( ).
A. 8 B. 5 C. 2.5 D.
10.如图,若将图(1)正方形剪成四块,恰能拼成图(2)的矩形,设a=1,则b等于( ).
二、填空题
11.一元二次方程 4x(x—2)=x—2 的解为 .
12.(2024·河南实验中学期末)若关于x 的一元二次方程 配方后得到方程(x+ 则a+c 的值为 .
13.(2024·淮北五校联考三模)某乡镇2021 年旅游总收入为50万元,到 2023 年旅游总收入达60.5万元.若每年的平均增长率相同,则年平均增长率是 .
14.(2024·河南周口西华期末)如图,数轴上点 A 代表的数字为3x+1,点B 代表的数字为 2x,已知AB=5,且点A 在数轴的负半轴上,则x的值为 .
15.(2023·眉山中考)已知方程 的根为 x ,x ,则 的值为 .
16.设x ,x 是一元二次方程 的两个实根,且 则a= .
三、解答题
17.中考新考法 过程纠错改错 阅读材料,并回答问题:
小明在学习一元二次方程时,
解方程 的过程如下:
解:∵a=2,b=--1,c=-3①,
=1-24=-23<0③,
∴此方程无解.
问题:(1)上述过程中,从 步开始出现了错误(填序号);
(2)发生错误的原因是: ;
(3)在下面的空白处,写出正确的解答过程.
18.中考新考法 解题方法型阅读理解题(2024·江苏苏州期中)阅读材料:为解方程 1)=0,我们可以将 视为一个整体,然后设 将原方程化为 解得
当y=0时,
当y=3时,
∴原方程的解为
由原方程得到①的过程,利用换元法达到了简化方程的目的,体现了整体转化的数学思想.
阅读后解答问题:
(1)利用上述材料中的方法解方程:
(2)已知一元二次方程. 的两根分别为--3,1,求方程a(2x+m- 的两根.
19.某平台爆红网络,某电商在该平台上直播带货,已知该产品的进货价为70元/件,为吸引流量,该电商在直播中承诺自家商品价格永远不会超过99元/件,根据一个月的市场调研,商家发现当售价为 110 元/件时,日销售量为20件,售价每降低1元,日销售量增加2件.
(1)当销售量为 30 件时,产品售价为 元/件.
(2)直接写出日销售量y(件)与售价x(元/件)的函数关系式.
(3)该产品的售价每件应定为多少,电商每天可盈利1200元
20.为推进生态文明建设,加快发展新能源汽车,国家对新能源汽车实行补贴政策.一家4S店从事某品牌纯电动汽车和插电式混动汽车两种新能源汽车(以下简称电动车和混动车)的销售,电动车每辆进价16万元,去年国家对该车每辆补贴4.5万元,补贴后每辆售价14万元;混动车每辆进价18万元,去年国家对该车每辆补贴2.8万元,补贴后每辆售价18万元.该4S店去年12月共销售这两种汽车120辆,获得利润324万元.
(1)该4S店去年12月销售了多少辆混动车
(2)今年国家对该品牌新能源汽车的补贴有所下降,电动车每辆比去年少补贴0.5万元,混动车每辆比去年少补贴0.8万元,该4S店为减少损失,今年1月把电动车的售价提高了m%,结果销量在去年12月的基础上减少
了 m%,对混动车的售价没有作调整,而销量在去年12月的基础上增加了2.4m辆,结果该4S店今年1月的利润比去年12月少了14万元,求m的值.
21.新情境设计花园 在一块长16m、宽12m的矩形荒地上建一个花园,要求花园所占面积为荒地面积的一半,图(1)是小明的设计方案,花园四周小路的宽度相等,通过解方程,小明得到小路的宽为2m 或12m.图(2)是小丽的设计方案,其中花园四个角上的扇形都相同.
(1)你认为小明的计算结果对吗 请说明理由.
(2)请你帮小丽求出图中的x.(精确到0.1)
(3)你还有其他的设计方案吗 请在图(3)中画出你设计的草图,并简要说明.
1. C [解析]∵ ∴x+1=4或x+1=-4.故选C.
2. B [解析]由题意,得常数项为0,则 0,(m-1)(m--2)=0,解得 又由一元二次方程概念可得m-1≠0,即m≠1.故m的值等于2.故选 B.
易错警示 本题考查一元二次方程的概念和解法.解答较易出现错误的是直接根据常数项为0解得m的值为1或2,忽略了一元二次方程中m≠1的隐含条件,造成错解.
3. A [解析] 12.故选 A.
4. C [解析]·
∴(2x-1)(x-1)=0,解得
∴方程 的两根都是正数.故选C.
5. C [解析]1个主干上的主干、支干和小分枝的总数是31个,其中枝干有x个,小分枝有x 个,于是可得方程 故选 C.
6. A [解析]设长方形的长等于a,宽等于b,因为长方形的长和宽是方程 的两个根,则 故长方形的周长=2(a+b)=2×3=6,长方形的面积 故选 A.
光速解法 根据题意,直接利用一元二次方程根与系数的关系,得到长方形长和宽的和与积,即可得到长方形的周长与面积.
7. B [解析]设运动员起跳到入水所用的时间是t秒,根据题意可知,-5(t-2)(t+1)=0,解得 -1(不合题意,舍去), 那么该运动员起跳到入水所用的时间是2秒.故选 B.
易错警示 解答本题时,要注意题意给出的是高度与时间的关系式,所以高度代入的是0不是10,故将高度代入所得的方程为-5(t-2)(t+1)=0,不是-5(t-2)(t+1)=10.
8. A [解析]由题意知, 解得
当第三边长是2时,2+3<6,不能构成三角形;
当第三边长是4时,三角形的周长为4+3+6=13.故选 A.
C [解析]∵∠ACB=90°,BC=BD=m,AC=6,
即
解得m=2.5或m=-2.5,根据题意m>0,∴m=2.5;经检验,m=2.5是原方程的解.故选C.
思路引导本题考查一元二次方程的应用,解题的关键是列出方程,难点是解方程: ,去分母,得 移项、合并同类项,得 即 由算术平方根的定义得 解得m=2.5(m>0).
10. B [解析]依题意,得(
又b不能为负, 故选B.
方法诠释本题是一个信息题目,首先正确理解题目的意思,然后根据题目隐含条件找到数量关系,再利用数量关系列出方程解决问题.根据图(1)可以知道图形是一个正方形,边长为(a+b),图(2)是一个长方形,长、宽分别为(b+a+b),b,并且它们的面积相等,由此即可列出等式( 而a=1,代入即可得到关于b的方程,解方程即可求出b.
[解析]移项,得4x(x-2)--(x-2)=0,提公因式,得(4x-1)(x-2)=0,解得.
易错警示 解答此方程时,不能直接根据等式性质将左右两边的(x-2)约去,因为当x--2=0时,左右两边也相等,即x=2时,方程也成立,故x=2是方程的一个根.
12.11 [解析]
移项,得
配方,得
∵方程 配方后得到
∴a=3,9-c=1,∴c=8,∴a+c=3+8=11.
思路引导先把常数项移到等号的另一边,方程的两边都加上一次项系数一半的平方后得新方程,根据题目中两个方程相等确定a,c,最后求出a+c.
13.10% [解析]设年平均增长率是x,利用该乡镇2023年旅游总收入=该乡镇2021年旅游总收入×(1+年平均增长率) ,可列出关于x 的一元二次方程 (不符合题意,舍去),∴年平均增长率是10%.
14.-2 [解析]根据题意,得 整理,得
∴(x-3)(x+2)=0,∴x-3=0或x+2=0,
当x=3时,3x+1=10>0,舍去,∴x的值为-2.
思路引导先利用数轴上两点之间的距离的求法得到 ,再把方程化为一般式为 ,接着利用因式分解法把方程转化为x-3=0或x+2=0,然后解两个一次方程,从而可得到满足条件的x的值.
15.6 [解析]∵方程 的根为x ,x ,
=-4+2×3+4=6.
解后反思 本题考查了一元二次方程根与系数的关系: 直接利用根与系数的关系作答.
16.10 [解析]由于x ,x 是. 的两个实数根, 于是 a-6=4,解得a=10.
17.(1)③
(2)计算结果错误(负数乘负数得负数).
(3)∵a=2,b=-1,c=-3,
18.(1)令 则
∴(m-2)(m+1)=0,∴m-2=0或m+1=0,解得m=2或m=-1.
当m=2时, 即 解得
当m=-1时, 即 解得
综上,原方程的解为
(2)∵一元二次方程 的两根分别为--3,1,
∴方程 中2x-4=-3或2x-4=1,解得 或
即方程 的两根分别是 和
●素养考向 本题主要考查换元法解一元二次方程,考查了模型观念、运算能力的核心素养,熟练掌握换元法和一元二次方程的解法是关键,体现了整体转化的数学思想.
19.(1)105
(2)根据题意,得y=20+2(110-x)=-2x+240.
∵该产品的进货价为70元/件,且该电商在直播中承诺自家商品价格永远不会超过99元/件,∴日销售量y(件)与售价x(元/件)的函数关系式为y=-2x+240(70≤x≤99).
(3)根据题意,得(x-70)(-2x+240)=1200,
整理,得
解得 (不符合题意,舍去).
故该产品的售价每件应定为90元.
20.(1)设该4S店去年12月销售了x辆混动车,则销售了(120-x)辆电动车.
由题意,得(14+4.5-16)(120-x)+(18+2.8-18)x=324,解得x=80.
故该4S店去年12月销售了80辆混动车.
(2)由题意,得[14(1+m%)+4-16]×(120-80)× 14,解得
当m=50时, 不符合题意,舍去.故m的值为10.
21.(1)小明的计算结果不对.理由如下:
设小路宽 ym,根据题意,得(16-2y)(12-2y)= 解得
因为荒地的宽为12m,所以 不符合题意,舍去.故取y=2,所以小路的宽为2m.
(2)由题意,得 所以 解得x≈±5.5.
因为扇形的半径不能为负数,所以取x≈5.5.
(3)如图所示,取四边中点,依次连接各边中点所得的四边形即为所要设计的花园的草图.(答案不唯一)
