20.2.1数据的集中趋势提优训练 (含答案)2024-2025学年沪科版八年级数学下册
文档属性
| 名称 | 20.2.1数据的集中趋势提优训练 (含答案)2024-2025学年沪科版八年级数学下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 188.8KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-15 21:17:24 | ||
图片预览




文档简介
20.2.1数据的集中趋势
第1课时 数据的集中趋势 (1)
1.一组数据2,2,3,3,4,4,则这组数据的平均数是( ).
A. 2 B. 2.5 C. 3 D. 4
2.学校“校园之声”广播站要选拔一名英语主持人,小莹参加选拔的各项成绩如下:
姓名 读 听 写
小莹 92 80 90
若把读、听、写的成绩按5 :3:2的比例计入个人的总分,则小莹的个人总分为( ).
A. 86 B. 87 C. 88 D. 89
3.(2023·长沙中考)睡眠管理作为“五项管理”中重要的内容之一,也是学校教育重点关注的内容.某老师了解到班上某位学生的5天睡眠时间(单位:小时)如下:10,9,10,8,8,则该学生这5天的平均睡眠时间是 小时.
4. 某校拟招聘一名优秀的数学教师,设置了笔试、面试、试讲三项水平测试,综合成绩按照笔试占30%,面试占30%,试讲占40%进行计算,小徐的三项测试成绩如图所示,则她的综合成绩为 分.
5.(2024·福建福州仓山区开学联考)甲、乙两数的平均数是16,甲、乙、丙三数的平均数是20,可算出丙数为 .
6.一位同学进行五次投实心球的练习,每次投出的成绩如表所示:
投实心球次序 1 2 3 4 5
成绩/m 10.5 10.2 10.3 10.6 10.4
求该同学这五次投实心球的平均成绩.
7.(2024·漳州模拟)某公司从德、能、勤、绩、廉五方面按3:2:1:2:2对员工进行年终考评.公司某职员在2023年度五个方面得分如图所示,则该职员的年终考评为 分.
8.(2024·辽宁沈阳沈北新区期末)某同学在八年级下学期参加了四次单元过关,以及期中和期末考试,所有考试的数学成绩如表所示.若根据如图所示的权重计算本学期的总评成绩,则该同学在本学期的总评成绩是 分.
测试类型 单元测试 期中 期末
1 2 3 4
成绩/分 90 85 86 89 90 88
9.新情境评选宣讲员 (2024·长治三模)辽宁,血脉中流淌着红色基因.经年岁月,淬炼生成了抗日战争起始地、解放战争转折地、新中国国歌素材地、抗美援朝出征地、共和国工业奠基地、雷锋精神发祥地的红色标识.为传承辽宁红色“六地”文化,某校准备组织学生开展宣讲活动.现需要从10名候选的学生中评选出2名宣讲员,评选活动分为三个阶段:
初选:九位评委对每名选手的宣讲文稿分别打分(满分10分,打分为整数),取平均分作为初选阶段的个人得分,按得分由高到低确定前5名选手进入复评阶段.
复评:进入复评阶段的5名选手进行现场宣讲,九位评委对每名选手的现场表现分别打分(满分10分,打分为整数),取平均分作为复评阶段的个人得分.
终选:将初选与复评两个阶段得分按3:7的比例计算选手个人最终得分,按得分由高到低确定前2名选手成为宣讲员.
学校收集、整理了选手的得分,其中部分信息如下:
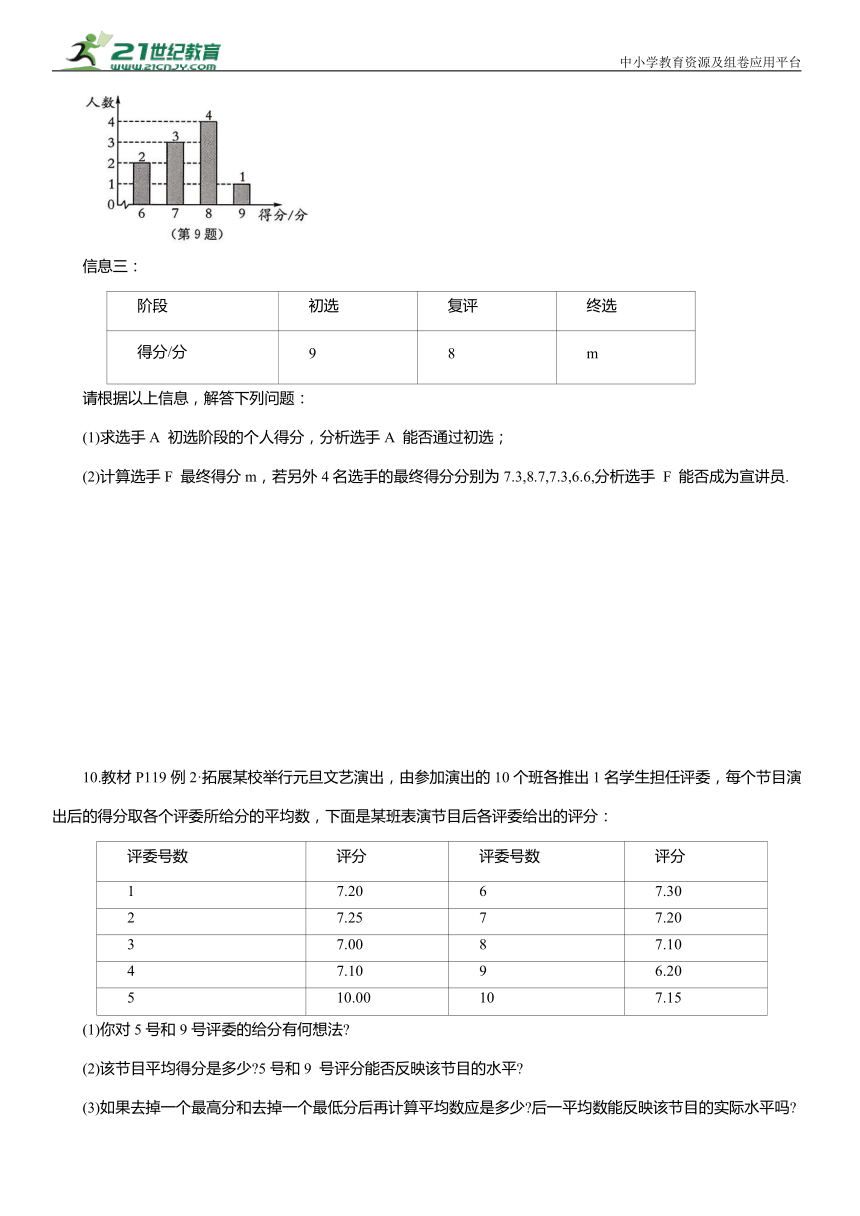
信息一:初选阶段九位评委对选手A 打分情况如下:7,8,8,9,8,9,7,8,8.
信息二:
初选阶段10名选手得分情况
信息三:
阶段 初选 复评 终选
得分/分 9 8 m
请根据以上信息,解答下列问题:
(1)求选手A 初选阶段的个人得分,分析选手A 能否通过初选;
(2)计算选手F 最终得分m,若另外4名选手的最终得分分别为7.3,8.7,7.3,6.6,分析选手 F 能否成为宣讲员.
10.教材P119例2·拓展某校举行元旦文艺演出,由参加演出的10个班各推出1名学生担任评委,每个节目演出后的得分取各个评委所给分的平均数,下面是某班表演节目后各评委给出的评分:
评委号数 评分 评委号数 评分
1 7.20 6 7.30
2 7.25 7 7.20
3 7.00 8 7.10
4 7.10 9 6.20
5 10.00 10 7.15
(1)你对5号和9号评委的给分有何想法
(2)该节目平均得分是多少 5号和9 号评分能否反映该节目的水平
(3)如果去掉一个最高分和去掉一个最低分后再计算平均数应是多少 后一平均数能反映该节目的实际水平吗
11.(2024·湖南衡阳耒阳开学联考)6位同学数学考试的平均成绩是92.5分,他们的成绩是互不相同的整数,最高的 99分,最低的76分,那么按分数从高到低居第3位的同学的分数至少是 分.
12.新情境 选拔篮球特色班学员 (2024·山东枣庄薛城区期末)自双减以来,同学们的课后延时服务活动丰富多彩,某学校在新的学期举办“篮球特色班”,大量热爱篮球的同学踊跃报名,但由于名额有限,所以需要考核选拔,考核的最终评价成绩由篮球知识、身体素质、篮球技能三项构成,下表是对甲、乙两名同学的成绩记录.
成绩/分
篮球知识 身体素质 篮球技能
甲 93 94 89
乙 88 90 95
(1)如果根据三项成绩的平均分确定最终评价成绩,计算说明谁将获胜.
(2)根据实际需要,将篮球知识、身体素质、篮球技能三项成绩按1:4:5的比例确定最终评价成绩,计算说明谁将获胜.
(3)如果你是“篮球特色班”的老师,请你制定一项标准来确定获胜人选,并说明制定该标准的理由.
13.(2024·福建中考)已知A,B 两地都只有甲、乙两类普通高中学校.在一次普通高中学业水平考试中,A地甲类学校有考生3000人,数学平均分为90分.乙类学校有考生2000人,数学平均分为80分.
(1)求A 地考生的数学平均分.
(2)若B 地甲类学校数学平均分为94分,乙类学校数学平均分为82分,据此,能否判断B 地考生数学平均分一定比A 地考生数学平均分高 若能,请给予证明.若不能,请举例说明.
第2课时 数据的集中趋势 (2)
1.(2024·贵州遵义期末)今年五一节,遵义高速交警对限速120km/h的某路段监测到6辆车的车速(单位: km/h)分别为118,106,105,120,118,112,则这组数据的众数为().
A. 115 B. 116 C. 118 D. 120
2.(2024·江苏徐州树德中学月考)数据1,2,4,5,3的中位数是 .
3.(2024·邯郸冀南新区模拟)为验收某校对学生“消防安全教育”的教学质量,教育局工作组在该校随机抽取了10名学生进行“消防安全”知识质量检测(得分均为整数分,满分100分).并规定:若学生成绩的平均分或中位数小于 80分,则该校此项工作不合格.把成绩进行整理分析后,制成如下统计图:
(1)求学生此次检测成绩的平均数和中位数,并判断该校此项工作是否合格.
(2)工作组从余下的学生中又随机抽取了两名进行答题,并和之前10名同学的数据整合在一起,重新计算后,发现数据的平均数变小,但中位数没有改变.已知这两名学生的分数相同,求这两名学生分数的最大值.
4.(2024·黑龙江牡丹江四中期末)一组数据1,3,5,x的平均数与中位数相同,则x 的值是( ).
A. 1或3或7 B. 1或3或5
C. - 1或3或7 D. - 1或3或5
5.(2024·陕西商洛山阳期末)若一组数据3,3,3,2,4,4,x,5有唯一的众数,则x 的值不可能为
6.某乡镇企业生产部有技术工人15人,生产部为了合理制定产品的每月生产定额,统计了这15人某月的加工零件个数(如下表).
每人加工 零件数/个 54 45 30 24 21 12
人数 1 1 2 6 3 2
(1)写出这15人该月加工零件数的平均数、中位数和众数.
(2)假设生产部负责人把每位工人的月加工零件数定为24件,你认为是否合理 为什么 如果不合理,请你设计一个较为合理的生产定额,并说明理由.
7.(2024·连云港中考)为了解七年级男生体能情况,某校随机抽取了七年级20名男生进行体能测试,并对测试成绩(单位:分)进行了统计分析:[收集数据]100,94,88,88,52,79,83,64,83,87,76,89,91,68,77,97,72,83,96,73.
中小学教育资源及组卷应用平台
[整理数据]该校规定:x≤59为不合格,59等次 频数/人数 频率
不合格 1 0.05
合格 a 0.20
良好 10 0.50
优秀 5 b
合计 20 1.00
[分析数据]此组数据的平均数是 82,众数是83,中位数是c.
[解决问题]
(1)填空:a= ,b= ,c=
(2)若该校七年级共有 300名男生,估计体能测试能达到优秀的男生有多少人
(3)根据上述统计分析情况,写一条你的看法.
8.新情境租车问题 (2024·南京秦淮区模拟)某公司有A,B,C三种型号电动汽车出租,每辆车每天费用分别为300元、380元、500 元.阳阳打算从该公司租一辆汽车外出旅游一天,往返行程为210km,为了选择合适的型号,通过网络调查,获得三种型号汽车充满电后的里程数据如图所示.
A,B,C三种型号电动汽车充满电后
能行驶里程的统计图
(1)阳阳已经对B,C型号汽车数据统计如下表,请在下表中填写A 型号汽车的平均里程、中位数、众数;
型号 平均里程/km 中位数/km 众数/ km
A
B 216 215 220
C 227.5 227.5 225
(2)为了尽可能避免行程中充电耽误时间,又能经济实惠地用车,请你从相关统计量和符合行程要求的百分比等进行分析,给出合理的用车型号建议.
9.某花店每天以每枝5元的价格从农场购进若干枝玫瑰花,然后以每枝10元的价格出售,如果当天卖不完,剩下的玫瑰花作垃圾处理.
(1)若花店一天购进16枝玫瑰花,求当天的利润y(单位:元)关于当天需求量n(单位:枝,n是自然数)的函数表达式.
(2)花店记录了100 天玫瑰花的日需求量(单位:枝),整理得如表:
日需求量n 14 15 16 17 18 19 20
频数 10 20 16 16 15 13 10
①这100个日需求量所组成的一组数据的中位数和众数分别是 , .
②以100天记录的各需求量的频率作为计算平均一天需求量对应的权重.若花店计划一天购进16枝或17枝玫瑰花,从盈利的角度分析,你认为应购进 16 枝还是 17 枝 请说明理由.
10.中考新考法 综合与实践 (2024·安徽中考)综合与实践
[项目背景]
无核柑橘是我省西南山区特产,该地区某村有甲、乙两块成龄无核柑橘园.在柑橘收获季节,班级同学前往该村开展综合实践活动,其中一个项目是:在日照、土质、空气湿度等外部环境基本一致的条件下,对两块柑橘园的优质柑橘情况进行调查统计,为柑橘园的发展规划提供一些参考.
[数据收集与整理]
从两块柑橘园采摘的柑橘中各随机选取200个.在技术人员指导下,测量每个柑橘的直径,作为样本数据.柑橘直径用x(单位:cm)表示.将所收集的样本数据进行如下分组:
组别 A B C D E
x 3.5≤x <4.5 4.5≤x <5.5 5.5≤x <6.5 6.5≤x <7.5 7.5≤x ≤8.5
整理样本数据,并绘制甲、乙两园样本数据的频数直方图,部分信息如下:
任务1 求图(1)中a 的值.
[数据分析与运用]
任务2 A,B,C,D,E五组数据的平均数分别取为4,5,6,7,8,计算乙园样本数据的平均数.
任务3 下列结论一定正确的是 .(填正确结论的序号)
①两园样本数据的中位数均在C 组;②两园样本数据的众数均在 C 组;③两园样本数据的最大数与最小数的差相等.
任务4 结合市场情况,将C,D两组的柑橘认定为一级,B组的柑橘认定为二级,其他组的柑橘认定为三级,其中一级柑橘的品质最优,二级次之,三级最次.试估计哪个园的柑橘品质更优,并说明理由.
根据所给信息,请完成以上所有任务.
1. C [解析]这组数据的平均数是 3.故选C.
思路引导 一组数据的平均数等于这组数据中所有数据之和除以数据的个数.
2. C [解析]根据题意,得 88(分).故选 C.
■易错警示 本题考查了加权平均数的计算方法,在进行计算时候注意权的分配,另外还应细心,否则很容易出错.
3.9 [解析](10+9+10+8+8)÷5=9(小时).
故该学生这5天的平均睡眠时间是9 小时.
■归纳总结 本题考查了平均数,平均数是指在一组数据中所有数据之和再除以数据的个数.它是反映数据集中趋势的一项指标.根据平均数的定义列式计算即可.
4.85.8 [解析]她的综合成绩为86×30%+80×30%+90×40%=85.8(分).
5.28 [解析]∵甲、乙两数的平均数是16,∴甲、乙两数的和为16×2=32.
∵甲、乙、丙三数的平均数是20,∴甲、乙、丙三数的和为20×3=60,∴丙数=60-32=28.
6.该同学这五次投实心球的平均成绩为 10.2+10.3+10.6+10.4)=10.4(m).
故该同学这五次投实心球的平均成绩为10.4m.
7.7.6 [解析]由题意得,该职员的年终考评为 (分).
8.88.55 [解析] 90×(1-10%-60%)+88×60%=88.55(分).
■思路引导 本题考查加权平均数.四次单元测试的平均成绩、期中成绩、期末成绩分别乘各自的权重,求其和即可.
9.(1)∵选手A 初选阶段的平均分为 9+8+9+7+8+8)=8(分),初选阶段的中位数为 (分),
∴选手A 初选阶段的平均分在前5名内,
∴选手A 能通过初选.
∵另外4名选手的最终得分分别为7.3,8.7,7.3,6.6,
∴选手 F 排在第二名.
∵按得分由高到低确定前2名选手成为宣讲员,
∴选手 F能成为宣讲员.
10.(1)所给分数分别偏高和偏低.
7.30+7.20+7.10+6.20+7.15)=7.35,5号和9号评分不能准确反映该节目的水平.
7.20+7.10+7.15)=7.1625,能反映.
11.95 [解析]92.5×6-99-76=380(分).按分数从高到低,由于最高分是99分,所以第2位的同学的最好成绩是98分,此时剩余三人成绩和为380—98=282(分).要使第3位的同学成绩最小,第4、5位的同学的成绩尽可能接近第3位的同学的成绩,则这3个数相差为1,282÷3=94(分),则第3位同学的分数至少是94+1=95(分).
思路引导 要求第3位的同学至少要考多少分,知道6位同学的总平均分,能求出总成绩,用总成绩一最高分—最低分=另4位同学的总成绩,要想第3位的同学成绩最小,则第2位的同学成绩取最大值为98,进而求出另3位的同学的总成绩,进而根据“总成绩÷总人数=平均分”能求出另3位同学的平均分,继而分析、推导得出所求问题的答案.
12.(1)甲的成绩为 (分),乙的成绩为 (分).
∵91<92,∴甲将获胜.
(2)甲的成绩为 (分),乙的成绩为 (分).
∵91.4<92.3,∴乙将获胜.
(3)答案不唯一,如:将篮球知识、身体素质、篮球技能三项成绩按2:3:5的比例确定最终评价成绩.理由:因为是“篮球特色班”,要重点关注的是篮球技能,所以将篮球知识、身体素质、篮球技能三项成绩按2:3:5的比例确定最终评价成绩.
思路引导 本题考查了算术平均数和加权平均数的计算.(1)利用算术平均数的定义求出甲、乙两名同学的成绩,再进行比较,即可得出答案;(2)根据加权平均数的定义列出算式,求出甲、乙两名同学的成绩,再进行比较,即可得出答案;(3)答案不唯一,合理即可.
13.(1)由题意,得A 地考生的数学平均分为 (90×3000+80×2000)=86(分).
(2)不能.
举例如下:如B地甲类学校有考生1000人,乙类学校有考生 3 000 人,则B 地考生的数学平均分为 (分),
因为85<86,所以不能判断B 地考生数学平均分一定比A 地考生数学平均分高.(答案不唯一,只要学生能作出正确判断,并且所举的例子能说明其判断即可)
第2课时 数据的集中趋势(2)
1. C [解析]数据118 出现了2次,最多,所以众数为118.故选C.
2.3
3.(1)平均数为 (分).
∵第5 和第6个数据都是80,∴中位数为80分.
∵学生成绩的平均分或中位数均不小于 80分,∴该校此项工作合格.
(2)设两名学生的分数为x分,
根据题意,得 解得x<81,
∵中位数没有改变,∴这两名学生分数的最大值为80分.
4. C [解析]①将这组数据从小到大的顺序排列为1,3,5,x,处于中间位置的两个数是3和5,
∴中位数是4.∵平均数与中位数相同,∴4=(1+3+5+x)÷4,解得x=7,符合排列顺序;
②将这组数据从小到大的顺序排列后为1,3,x,5,中位数是
∵平均数与中位数相同, 4,解得x=3,符合排列顺序;③将这组数据从小到大的顺序排列后为1,x,3,5,中位数是
∵平均数与中位数相同, 4,解得x=3,符合排列顺序;
④将这组数据从小到大的顺序排列后为x,1,3,5,则89中位数是2.
∵平均数与中位数相同,∴2=(x+1+3+5)÷4,解得x=-1,符合排列顺序.
综上所述,x的值为-1或3或7.故选C.
■ 易错警示 本题考查了确定一组数据的中位数,涉及到分类讨论思想,要明确中位数的值与大小排列顺序有关,一些学生往往对这个概念掌握不清楚,计算方法不明确而解答不完整.注意找中位数的时候一定要先排好顺序,然后再根据奇数和偶数个来确定中位数.若数据有奇数个,则正中间的数字即为所求.若是偶数个,则找中间两位数的平均数.
5.4 [解析]在3,3,3,2,4,4,x,5这组数据中,数据3出现了3次,4出现了2次,且有唯一的众数,∴唯一的众数是3,∴x的值不可能为4.
6.(1)平均数 26(件),
将表格中的数据按从大到小的顺序排列为54,45,30,30,24,24,24,24,24,24,21,21,21,12,12,可得第8名工人加工零件数为24件,且零件加工数为24件的工人最多.
故该15 人该月加工的零件数的平均数为26,中位数为24,众数为24.
(2)24件较为合理,24 既是众数,也是中位数,且24小于人均零件加工数,是大多数人所能达到的生产定额.
7.(1)4 0.25 83 [解析]a=20×0.2=4,b=1-0.05-0.20-0.50=0.25,中位数 (2)300×0.25=75(人).
故估计七年级300名男生中有75人体能测试能达到优秀.
(3)平时应加强体能训练.(答案不唯一,合理即可)
8.(1)A型号汽车的平均里程为
将A 型号汽车的20个数据按从小到大的顺序排列,第10、第11个数据均为200km,
∴中位数为200 km.
∵205出现了六次,次数最多,∴众数为205.
(2)选择B 型号汽车,理由如下:A型号汽车的平均里程、中位数和众数均低于 210km,且只有10%的车辆能达到行程要求,故不建议选择. B,C型号汽车的平均里程、中位数和众数都超过 210 km,其中B 型号汽车有 90%符合行程要求,很大程度上可以避免行程中充电耽误时间,且B 型号汽车比C型号汽车更经济实惠,故建议选择 B 型号汽车.
思路引导 本题考查了折线统计图、算术平均数、中位数和众数的定义.(1)根据平均数、中位数、众数的定义即可求解;(2)根据平均数、中位数、众数的意义,结合往返行程为210km、三种型号电动汽车租车费用即可作出判断.
9.(1)当n≥16时,y=16×(10-5)=80;
当n≤15时,y=5n-5(16-n)=10n-80,
(2)①17 15
②平均一天的需求量:(14×10+15×20+16×16+ 16.85(枝),
当购进16枝时,利润为(14×5-2×5)×0.1+(15×5-5)×0.2+16×5×(1-0.1-0.2)=76(元).
当购进17枝时,利润为(14×5-3×5)×0.1+(15×5-2×5)×0.2+(16×5-5)×0.16+17×5×(1-0.1-0.2-0.16)=76.4(元).
因为76.4>76,所以应购进17枝.
思路引导 本题考查分段函数模型的建立,考查众数及中位数的定义,考查学生利用数学知识解决实际问题的能力.(1)根据卖出一枝可得利润5元,卖不出一枝可得赔本5元,即可建立分段函数;(2)①利用众数中位数的定义求解即可;②求出购进17枝时当天的利润,与购进16枝玫瑰花时当天的利润比较,即可得到结论.
10.任务1:由题意,得 a =200--(15+70+50+25)=40.
任务2: ×(15×4+50×5+70×6+50×7+15×8)=6.故乙园样本数据的平均数为6.
任务3:① [解析]由统计图,可知两园样本数据的中位数均在 C 组,故①结论正确;甲园的众数在B组,乙园的众数在C组,故②结论错误;两园样本数据的最大数与最小数的差不一定相等,故③结论错误.
任务4:乙园的柑橘品质更优.理由如下:
由样本数据频数直方图,可得乙园一级柑橘所占比例大于甲园,因此可以认为乙园的柑橘品质更优.
知识拓展 平均数是指在一组数据中所有数据之和再除以数据的个数.一组数据的中位数与这组数据的排序及数据个数有关,因此求一组数据的中位数时,先将该组数据按从小到大(或按从大到小)的顺序排列,然后根据数据的个数确定中位数:当数据个数为奇数时,则中间的一个数即为这组数据的中位数;当数据个数为偶数时,则最中间的两个数的算术平均数即为这组数据的中位数.平均数、中位数、众数描述了数据的集中趋势.
第1课时 数据的集中趋势 (1)
1.一组数据2,2,3,3,4,4,则这组数据的平均数是( ).
A. 2 B. 2.5 C. 3 D. 4
2.学校“校园之声”广播站要选拔一名英语主持人,小莹参加选拔的各项成绩如下:
姓名 读 听 写
小莹 92 80 90
若把读、听、写的成绩按5 :3:2的比例计入个人的总分,则小莹的个人总分为( ).
A. 86 B. 87 C. 88 D. 89
3.(2023·长沙中考)睡眠管理作为“五项管理”中重要的内容之一,也是学校教育重点关注的内容.某老师了解到班上某位学生的5天睡眠时间(单位:小时)如下:10,9,10,8,8,则该学生这5天的平均睡眠时间是 小时.
4. 某校拟招聘一名优秀的数学教师,设置了笔试、面试、试讲三项水平测试,综合成绩按照笔试占30%,面试占30%,试讲占40%进行计算,小徐的三项测试成绩如图所示,则她的综合成绩为 分.
5.(2024·福建福州仓山区开学联考)甲、乙两数的平均数是16,甲、乙、丙三数的平均数是20,可算出丙数为 .
6.一位同学进行五次投实心球的练习,每次投出的成绩如表所示:
投实心球次序 1 2 3 4 5
成绩/m 10.5 10.2 10.3 10.6 10.4
求该同学这五次投实心球的平均成绩.
7.(2024·漳州模拟)某公司从德、能、勤、绩、廉五方面按3:2:1:2:2对员工进行年终考评.公司某职员在2023年度五个方面得分如图所示,则该职员的年终考评为 分.
8.(2024·辽宁沈阳沈北新区期末)某同学在八年级下学期参加了四次单元过关,以及期中和期末考试,所有考试的数学成绩如表所示.若根据如图所示的权重计算本学期的总评成绩,则该同学在本学期的总评成绩是 分.
测试类型 单元测试 期中 期末
1 2 3 4
成绩/分 90 85 86 89 90 88
9.新情境评选宣讲员 (2024·长治三模)辽宁,血脉中流淌着红色基因.经年岁月,淬炼生成了抗日战争起始地、解放战争转折地、新中国国歌素材地、抗美援朝出征地、共和国工业奠基地、雷锋精神发祥地的红色标识.为传承辽宁红色“六地”文化,某校准备组织学生开展宣讲活动.现需要从10名候选的学生中评选出2名宣讲员,评选活动分为三个阶段:
初选:九位评委对每名选手的宣讲文稿分别打分(满分10分,打分为整数),取平均分作为初选阶段的个人得分,按得分由高到低确定前5名选手进入复评阶段.
复评:进入复评阶段的5名选手进行现场宣讲,九位评委对每名选手的现场表现分别打分(满分10分,打分为整数),取平均分作为复评阶段的个人得分.
终选:将初选与复评两个阶段得分按3:7的比例计算选手个人最终得分,按得分由高到低确定前2名选手成为宣讲员.
学校收集、整理了选手的得分,其中部分信息如下:
信息一:初选阶段九位评委对选手A 打分情况如下:7,8,8,9,8,9,7,8,8.
信息二:
初选阶段10名选手得分情况
信息三:
阶段 初选 复评 终选
得分/分 9 8 m
请根据以上信息,解答下列问题:
(1)求选手A 初选阶段的个人得分,分析选手A 能否通过初选;
(2)计算选手F 最终得分m,若另外4名选手的最终得分分别为7.3,8.7,7.3,6.6,分析选手 F 能否成为宣讲员.
10.教材P119例2·拓展某校举行元旦文艺演出,由参加演出的10个班各推出1名学生担任评委,每个节目演出后的得分取各个评委所给分的平均数,下面是某班表演节目后各评委给出的评分:
评委号数 评分 评委号数 评分
1 7.20 6 7.30
2 7.25 7 7.20
3 7.00 8 7.10
4 7.10 9 6.20
5 10.00 10 7.15
(1)你对5号和9号评委的给分有何想法
(2)该节目平均得分是多少 5号和9 号评分能否反映该节目的水平
(3)如果去掉一个最高分和去掉一个最低分后再计算平均数应是多少 后一平均数能反映该节目的实际水平吗
11.(2024·湖南衡阳耒阳开学联考)6位同学数学考试的平均成绩是92.5分,他们的成绩是互不相同的整数,最高的 99分,最低的76分,那么按分数从高到低居第3位的同学的分数至少是 分.
12.新情境 选拔篮球特色班学员 (2024·山东枣庄薛城区期末)自双减以来,同学们的课后延时服务活动丰富多彩,某学校在新的学期举办“篮球特色班”,大量热爱篮球的同学踊跃报名,但由于名额有限,所以需要考核选拔,考核的最终评价成绩由篮球知识、身体素质、篮球技能三项构成,下表是对甲、乙两名同学的成绩记录.
成绩/分
篮球知识 身体素质 篮球技能
甲 93 94 89
乙 88 90 95
(1)如果根据三项成绩的平均分确定最终评价成绩,计算说明谁将获胜.
(2)根据实际需要,将篮球知识、身体素质、篮球技能三项成绩按1:4:5的比例确定最终评价成绩,计算说明谁将获胜.
(3)如果你是“篮球特色班”的老师,请你制定一项标准来确定获胜人选,并说明制定该标准的理由.
13.(2024·福建中考)已知A,B 两地都只有甲、乙两类普通高中学校.在一次普通高中学业水平考试中,A地甲类学校有考生3000人,数学平均分为90分.乙类学校有考生2000人,数学平均分为80分.
(1)求A 地考生的数学平均分.
(2)若B 地甲类学校数学平均分为94分,乙类学校数学平均分为82分,据此,能否判断B 地考生数学平均分一定比A 地考生数学平均分高 若能,请给予证明.若不能,请举例说明.
第2课时 数据的集中趋势 (2)
1.(2024·贵州遵义期末)今年五一节,遵义高速交警对限速120km/h的某路段监测到6辆车的车速(单位: km/h)分别为118,106,105,120,118,112,则这组数据的众数为().
A. 115 B. 116 C. 118 D. 120
2.(2024·江苏徐州树德中学月考)数据1,2,4,5,3的中位数是 .
3.(2024·邯郸冀南新区模拟)为验收某校对学生“消防安全教育”的教学质量,教育局工作组在该校随机抽取了10名学生进行“消防安全”知识质量检测(得分均为整数分,满分100分).并规定:若学生成绩的平均分或中位数小于 80分,则该校此项工作不合格.把成绩进行整理分析后,制成如下统计图:
(1)求学生此次检测成绩的平均数和中位数,并判断该校此项工作是否合格.
(2)工作组从余下的学生中又随机抽取了两名进行答题,并和之前10名同学的数据整合在一起,重新计算后,发现数据的平均数变小,但中位数没有改变.已知这两名学生的分数相同,求这两名学生分数的最大值.
4.(2024·黑龙江牡丹江四中期末)一组数据1,3,5,x的平均数与中位数相同,则x 的值是( ).
A. 1或3或7 B. 1或3或5
C. - 1或3或7 D. - 1或3或5
5.(2024·陕西商洛山阳期末)若一组数据3,3,3,2,4,4,x,5有唯一的众数,则x 的值不可能为
6.某乡镇企业生产部有技术工人15人,生产部为了合理制定产品的每月生产定额,统计了这15人某月的加工零件个数(如下表).
每人加工 零件数/个 54 45 30 24 21 12
人数 1 1 2 6 3 2
(1)写出这15人该月加工零件数的平均数、中位数和众数.
(2)假设生产部负责人把每位工人的月加工零件数定为24件,你认为是否合理 为什么 如果不合理,请你设计一个较为合理的生产定额,并说明理由.
7.(2024·连云港中考)为了解七年级男生体能情况,某校随机抽取了七年级20名男生进行体能测试,并对测试成绩(单位:分)进行了统计分析:[收集数据]100,94,88,88,52,79,83,64,83,87,76,89,91,68,77,97,72,83,96,73.
中小学教育资源及组卷应用平台
[整理数据]该校规定:x≤59为不合格,59
不合格 1 0.05
合格 a 0.20
良好 10 0.50
优秀 5 b
合计 20 1.00
[分析数据]此组数据的平均数是 82,众数是83,中位数是c.
[解决问题]
(1)填空:a= ,b= ,c=
(2)若该校七年级共有 300名男生,估计体能测试能达到优秀的男生有多少人
(3)根据上述统计分析情况,写一条你的看法.
8.新情境租车问题 (2024·南京秦淮区模拟)某公司有A,B,C三种型号电动汽车出租,每辆车每天费用分别为300元、380元、500 元.阳阳打算从该公司租一辆汽车外出旅游一天,往返行程为210km,为了选择合适的型号,通过网络调查,获得三种型号汽车充满电后的里程数据如图所示.
A,B,C三种型号电动汽车充满电后
能行驶里程的统计图
(1)阳阳已经对B,C型号汽车数据统计如下表,请在下表中填写A 型号汽车的平均里程、中位数、众数;
型号 平均里程/km 中位数/km 众数/ km
A
B 216 215 220
C 227.5 227.5 225
(2)为了尽可能避免行程中充电耽误时间,又能经济实惠地用车,请你从相关统计量和符合行程要求的百分比等进行分析,给出合理的用车型号建议.
9.某花店每天以每枝5元的价格从农场购进若干枝玫瑰花,然后以每枝10元的价格出售,如果当天卖不完,剩下的玫瑰花作垃圾处理.
(1)若花店一天购进16枝玫瑰花,求当天的利润y(单位:元)关于当天需求量n(单位:枝,n是自然数)的函数表达式.
(2)花店记录了100 天玫瑰花的日需求量(单位:枝),整理得如表:
日需求量n 14 15 16 17 18 19 20
频数 10 20 16 16 15 13 10
①这100个日需求量所组成的一组数据的中位数和众数分别是 , .
②以100天记录的各需求量的频率作为计算平均一天需求量对应的权重.若花店计划一天购进16枝或17枝玫瑰花,从盈利的角度分析,你认为应购进 16 枝还是 17 枝 请说明理由.
10.中考新考法 综合与实践 (2024·安徽中考)综合与实践
[项目背景]
无核柑橘是我省西南山区特产,该地区某村有甲、乙两块成龄无核柑橘园.在柑橘收获季节,班级同学前往该村开展综合实践活动,其中一个项目是:在日照、土质、空气湿度等外部环境基本一致的条件下,对两块柑橘园的优质柑橘情况进行调查统计,为柑橘园的发展规划提供一些参考.
[数据收集与整理]
从两块柑橘园采摘的柑橘中各随机选取200个.在技术人员指导下,测量每个柑橘的直径,作为样本数据.柑橘直径用x(单位:cm)表示.将所收集的样本数据进行如下分组:
组别 A B C D E
x 3.5≤x <4.5 4.5≤x <5.5 5.5≤x <6.5 6.5≤x <7.5 7.5≤x ≤8.5
整理样本数据,并绘制甲、乙两园样本数据的频数直方图,部分信息如下:
任务1 求图(1)中a 的值.
[数据分析与运用]
任务2 A,B,C,D,E五组数据的平均数分别取为4,5,6,7,8,计算乙园样本数据的平均数.
任务3 下列结论一定正确的是 .(填正确结论的序号)
①两园样本数据的中位数均在C 组;②两园样本数据的众数均在 C 组;③两园样本数据的最大数与最小数的差相等.
任务4 结合市场情况,将C,D两组的柑橘认定为一级,B组的柑橘认定为二级,其他组的柑橘认定为三级,其中一级柑橘的品质最优,二级次之,三级最次.试估计哪个园的柑橘品质更优,并说明理由.
根据所给信息,请完成以上所有任务.
1. C [解析]这组数据的平均数是 3.故选C.
思路引导 一组数据的平均数等于这组数据中所有数据之和除以数据的个数.
2. C [解析]根据题意,得 88(分).故选 C.
■易错警示 本题考查了加权平均数的计算方法,在进行计算时候注意权的分配,另外还应细心,否则很容易出错.
3.9 [解析](10+9+10+8+8)÷5=9(小时).
故该学生这5天的平均睡眠时间是9 小时.
■归纳总结 本题考查了平均数,平均数是指在一组数据中所有数据之和再除以数据的个数.它是反映数据集中趋势的一项指标.根据平均数的定义列式计算即可.
4.85.8 [解析]她的综合成绩为86×30%+80×30%+90×40%=85.8(分).
5.28 [解析]∵甲、乙两数的平均数是16,∴甲、乙两数的和为16×2=32.
∵甲、乙、丙三数的平均数是20,∴甲、乙、丙三数的和为20×3=60,∴丙数=60-32=28.
6.该同学这五次投实心球的平均成绩为 10.2+10.3+10.6+10.4)=10.4(m).
故该同学这五次投实心球的平均成绩为10.4m.
7.7.6 [解析]由题意得,该职员的年终考评为 (分).
8.88.55 [解析] 90×(1-10%-60%)+88×60%=88.55(分).
■思路引导 本题考查加权平均数.四次单元测试的平均成绩、期中成绩、期末成绩分别乘各自的权重,求其和即可.
9.(1)∵选手A 初选阶段的平均分为 9+8+9+7+8+8)=8(分),初选阶段的中位数为 (分),
∴选手A 初选阶段的平均分在前5名内,
∴选手A 能通过初选.
∵另外4名选手的最终得分分别为7.3,8.7,7.3,6.6,
∴选手 F 排在第二名.
∵按得分由高到低确定前2名选手成为宣讲员,
∴选手 F能成为宣讲员.
10.(1)所给分数分别偏高和偏低.
7.30+7.20+7.10+6.20+7.15)=7.35,5号和9号评分不能准确反映该节目的水平.
7.20+7.10+7.15)=7.1625,能反映.
11.95 [解析]92.5×6-99-76=380(分).按分数从高到低,由于最高分是99分,所以第2位的同学的最好成绩是98分,此时剩余三人成绩和为380—98=282(分).要使第3位的同学成绩最小,第4、5位的同学的成绩尽可能接近第3位的同学的成绩,则这3个数相差为1,282÷3=94(分),则第3位同学的分数至少是94+1=95(分).
思路引导 要求第3位的同学至少要考多少分,知道6位同学的总平均分,能求出总成绩,用总成绩一最高分—最低分=另4位同学的总成绩,要想第3位的同学成绩最小,则第2位的同学成绩取最大值为98,进而求出另3位的同学的总成绩,进而根据“总成绩÷总人数=平均分”能求出另3位同学的平均分,继而分析、推导得出所求问题的答案.
12.(1)甲的成绩为 (分),乙的成绩为 (分).
∵91<92,∴甲将获胜.
(2)甲的成绩为 (分),乙的成绩为 (分).
∵91.4<92.3,∴乙将获胜.
(3)答案不唯一,如:将篮球知识、身体素质、篮球技能三项成绩按2:3:5的比例确定最终评价成绩.理由:因为是“篮球特色班”,要重点关注的是篮球技能,所以将篮球知识、身体素质、篮球技能三项成绩按2:3:5的比例确定最终评价成绩.
思路引导 本题考查了算术平均数和加权平均数的计算.(1)利用算术平均数的定义求出甲、乙两名同学的成绩,再进行比较,即可得出答案;(2)根据加权平均数的定义列出算式,求出甲、乙两名同学的成绩,再进行比较,即可得出答案;(3)答案不唯一,合理即可.
13.(1)由题意,得A 地考生的数学平均分为 (90×3000+80×2000)=86(分).
(2)不能.
举例如下:如B地甲类学校有考生1000人,乙类学校有考生 3 000 人,则B 地考生的数学平均分为 (分),
因为85<86,所以不能判断B 地考生数学平均分一定比A 地考生数学平均分高.(答案不唯一,只要学生能作出正确判断,并且所举的例子能说明其判断即可)
第2课时 数据的集中趋势(2)
1. C [解析]数据118 出现了2次,最多,所以众数为118.故选C.
2.3
3.(1)平均数为 (分).
∵第5 和第6个数据都是80,∴中位数为80分.
∵学生成绩的平均分或中位数均不小于 80分,∴该校此项工作合格.
(2)设两名学生的分数为x分,
根据题意,得 解得x<81,
∵中位数没有改变,∴这两名学生分数的最大值为80分.
4. C [解析]①将这组数据从小到大的顺序排列为1,3,5,x,处于中间位置的两个数是3和5,
∴中位数是4.∵平均数与中位数相同,∴4=(1+3+5+x)÷4,解得x=7,符合排列顺序;
②将这组数据从小到大的顺序排列后为1,3,x,5,中位数是
∵平均数与中位数相同, 4,解得x=3,符合排列顺序;③将这组数据从小到大的顺序排列后为1,x,3,5,中位数是
∵平均数与中位数相同, 4,解得x=3,符合排列顺序;
④将这组数据从小到大的顺序排列后为x,1,3,5,则89中位数是2.
∵平均数与中位数相同,∴2=(x+1+3+5)÷4,解得x=-1,符合排列顺序.
综上所述,x的值为-1或3或7.故选C.
■ 易错警示 本题考查了确定一组数据的中位数,涉及到分类讨论思想,要明确中位数的值与大小排列顺序有关,一些学生往往对这个概念掌握不清楚,计算方法不明确而解答不完整.注意找中位数的时候一定要先排好顺序,然后再根据奇数和偶数个来确定中位数.若数据有奇数个,则正中间的数字即为所求.若是偶数个,则找中间两位数的平均数.
5.4 [解析]在3,3,3,2,4,4,x,5这组数据中,数据3出现了3次,4出现了2次,且有唯一的众数,∴唯一的众数是3,∴x的值不可能为4.
6.(1)平均数 26(件),
将表格中的数据按从大到小的顺序排列为54,45,30,30,24,24,24,24,24,24,21,21,21,12,12,可得第8名工人加工零件数为24件,且零件加工数为24件的工人最多.
故该15 人该月加工的零件数的平均数为26,中位数为24,众数为24.
(2)24件较为合理,24 既是众数,也是中位数,且24小于人均零件加工数,是大多数人所能达到的生产定额.
7.(1)4 0.25 83 [解析]a=20×0.2=4,b=1-0.05-0.20-0.50=0.25,中位数 (2)300×0.25=75(人).
故估计七年级300名男生中有75人体能测试能达到优秀.
(3)平时应加强体能训练.(答案不唯一,合理即可)
8.(1)A型号汽车的平均里程为
将A 型号汽车的20个数据按从小到大的顺序排列,第10、第11个数据均为200km,
∴中位数为200 km.
∵205出现了六次,次数最多,∴众数为205.
(2)选择B 型号汽车,理由如下:A型号汽车的平均里程、中位数和众数均低于 210km,且只有10%的车辆能达到行程要求,故不建议选择. B,C型号汽车的平均里程、中位数和众数都超过 210 km,其中B 型号汽车有 90%符合行程要求,很大程度上可以避免行程中充电耽误时间,且B 型号汽车比C型号汽车更经济实惠,故建议选择 B 型号汽车.
思路引导 本题考查了折线统计图、算术平均数、中位数和众数的定义.(1)根据平均数、中位数、众数的定义即可求解;(2)根据平均数、中位数、众数的意义,结合往返行程为210km、三种型号电动汽车租车费用即可作出判断.
9.(1)当n≥16时,y=16×(10-5)=80;
当n≤15时,y=5n-5(16-n)=10n-80,
(2)①17 15
②平均一天的需求量:(14×10+15×20+16×16+ 16.85(枝),
当购进16枝时,利润为(14×5-2×5)×0.1+(15×5-5)×0.2+16×5×(1-0.1-0.2)=76(元).
当购进17枝时,利润为(14×5-3×5)×0.1+(15×5-2×5)×0.2+(16×5-5)×0.16+17×5×(1-0.1-0.2-0.16)=76.4(元).
因为76.4>76,所以应购进17枝.
思路引导 本题考查分段函数模型的建立,考查众数及中位数的定义,考查学生利用数学知识解决实际问题的能力.(1)根据卖出一枝可得利润5元,卖不出一枝可得赔本5元,即可建立分段函数;(2)①利用众数中位数的定义求解即可;②求出购进17枝时当天的利润,与购进16枝玫瑰花时当天的利润比较,即可得到结论.
10.任务1:由题意,得 a =200--(15+70+50+25)=40.
任务2: ×(15×4+50×5+70×6+50×7+15×8)=6.故乙园样本数据的平均数为6.
任务3:① [解析]由统计图,可知两园样本数据的中位数均在 C 组,故①结论正确;甲园的众数在B组,乙园的众数在C组,故②结论错误;两园样本数据的最大数与最小数的差不一定相等,故③结论错误.
任务4:乙园的柑橘品质更优.理由如下:
由样本数据频数直方图,可得乙园一级柑橘所占比例大于甲园,因此可以认为乙园的柑橘品质更优.
知识拓展 平均数是指在一组数据中所有数据之和再除以数据的个数.一组数据的中位数与这组数据的排序及数据个数有关,因此求一组数据的中位数时,先将该组数据按从小到大(或按从大到小)的顺序排列,然后根据数据的个数确定中位数:当数据个数为奇数时,则中间的一个数即为这组数据的中位数;当数据个数为偶数时,则最中间的两个数的算术平均数即为这组数据的中位数.平均数、中位数、众数描述了数据的集中趋势.
