实际应用问题期末专题整合提优(四) 提优训练 (含答案)
文档属性
| 名称 | 实际应用问题期末专题整合提优(四) 提优训练 (含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 245.9KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-15 17:45:06 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
实际应用问题期末专题整合提优(四)
一、选择题
1.跨学科 导线问题 (2024·山东聊城阳谷期末)电流通过导线时会产生热量,电流I(单位:A)、导线电阻R(单位:Ω)、通电时间t(单位:s)与产生的热量Q(单位:J)满足 已知导线的电阻为2Ω,1s时间导线产生50J的热量,电流I 的值是( ).
A. 2 B. 5 C. 8 D. 10
2.某校随机抽查了八年级的30名女生,测试了1分钟仰卧起坐的次数,并绘制成如图的频数分布直方图(每组含前一个边界,不含后一个边界),则次数不低于42个的有( ).
A. 6名 B. 8名 C. 14名 D. 23名
3.(2024·安徽蚌埠期末)如图,长方形内有两个相邻的正方形,其面积分别为6 和24,则图中阴影部分面积为( ).
A. 5 B. 5 C. 6 D. 6
4.小刚准备测量一段河水的深度,他把一根竹竿插到离岸边1.5m远的水底,竹竿高出水面0.5m,把竹竿的顶端拉向岸边,竿顶和岸边的水面刚好相齐,则河水的深度为( ).
A. 2m B. 2. 5m C. 2.25 m D. 3m
5.如果要用正三角形和正方形两种图形进行密铺,那么至少需要( ).
A.三个正三角形和两个正方形
B.两个正三角形和三个正方形
C.两个正三角形和两个正方形
D.三个正三角形和三个正方形
6.(2024·盐城模拟)某校射击队从甲、乙、丙、丁四人中选拔一人参加市运会射击比赛.在选拔赛中,每人射击10次,他们 10 次成绩的平均数及方差如下表所示:
甲 乙 丙 丁
平均数/环 9.7 9.5 9.5 9.7
方差/环 5.1 4.7 4.5 4.5
请你根据表中数据选一人参加比赛,最合适的人选是( ).
A. 甲 B. 乙 C. 丙 D. 丁
7.传统文化 《田亩比类乘除捷法》(2024·安徽亳州期末)我国南宋数学家杨辉在1275年提出了一个问题:直田积(矩形面积)八百六十四步(平方步),只云阔(宽)不及长一十二步(宽比长少一十二步),则“阔”是( ).
A. 12步 B. 24步 C. 36步 D. 72步
8.(2024·安徽安庆期中)甲流病毒是一种传染性极强的急性呼吸道传染病,感染者的临床以发热、乏力、干咳为主要表现.在“甲流”初期,有1人感染了“甲流病毒”,如若得不到有效控制,经过两轮传染后共有225人感染了“甲流病毒”,则每轮传染中平均一个人传染了( ).
A. 11人 B. 12人 C. 13人 D. 14人
9.如图,长方体敞口玻璃罐的长、宽、高分别为16cm,6cm和6cm,在罐内点E 处有一小块饼干碎末,此时一只蚂蚁正好在罐外壁,在长方形 ABCD 中心的正上方2cm 的点 H 处,则蚂蚁到达饼干的最短距离是( ).
A. 24cm B. 18cm
10.(2024·天津河西区一模)把一根长为80cm的绳子剪成两段,并把每一段绳子都围成一个正方形,如图所示,有以下结论:
①当AF 的长是12cm时,BC 的长为8cm;
②这两个正方形的面积之和可以是198cm ;
③这两个正方形的面积之和可以是288cm .其中,正确结论的个数是().
A. 0 B. 1 C. 2 D. 3
二、填空题
11.某校规定学生的体育成绩由三部分组成,早晨锻炼及体育课外活动表现占成绩的15%,体育理论测试占35%,体育技能测试占50%,小明的上述三项成绩依次是94分,90分,96分,则小明这学期的体育成绩是 分.
12. 新情境 平面镶嵌 (2024·榆林高新区二模)某广场的地面是由相同的正五边形与相同的四角星形(四个尖角的度数相同)铺成的无缝隙、不重叠的图形,如图是该广场地面的一部分,则图中四角星形的尖角∠ABC 的度数为 .
13.为迎接期末体育测试,小强每天坚持引体向上锻炼,他记录了某一周每天做引体向上的个数,如下表:
星期 日 一 二 三 四 五 六
个数 11 12 13 12
其中有三天的个数被墨汁覆盖了,但小强已经计算出这组数据的唯一众数是13,平均数是12,那么这组数据的方差是 .
14.如图所示,小强从A 点出发,沿直线前进10米后左转 24°,再沿直线前进 10 米,又向左转24°,…,照这样走下去,他第一次回到出发地A 点时,一共走的路程是 .
15.中考新考法 动点问题(2024·安徽淮南田家庵区月考)如图,在四边形 ABCD 中,AB∥CD,∠BCD=90°,BC=8cm,AB=AD=10cm,点 P 从点A 出发,以每秒3c m 的速度沿折线A-B-C方向运动,点Q 从点 D 出发,以每秒2cm速度沿线段 DC 方向向点C运动.已知动点 P,Q 同时出发,当点 Q 运动到点C时,P,Q运动停止,设运动时间为t.
(1)当t= 秒时,四边形 PBQD 为平行四边形;
(2)在点 P,点Q 的运动过程中,当t = 秒时,△BPQ 的面积为15 cm .
三、解答题
16.新情境 方案选择 (2024·陕西安康旬阳期末)快递公司为顾客交寄的快递提供纸箱包装服务,现有三款包装纸箱,底面规格如下表:
型号 长 宽
小号 20cm 18cm
中号 25 cm 20cm
大号 30cm 25cm
已知甲、乙两件礼品底面都是正方形,底面积分别为80cm ,180cm 若要将它们合在一个包装箱中寄出,底面摆放方式如图,从节约材料的角度考虑,应选择哪种底面型号的纸箱 请说明理由.
乙的底面
甲的底面
(第16题)
17.(2024·泰州二中附中三模)我国快递行业迅速发展,经调查,某快递公司今年2月份投递快递总件数为 20万件,4月份投递快递总件数33.8万件,假设该公司每月投递快递总件数的增长率相同.
(1)求该公司投递快递总件数的月增长率.
(2)如果该公司每月投递快递总件数的增长率保持不变,那么5月份投递快递总件数是否达到45万件
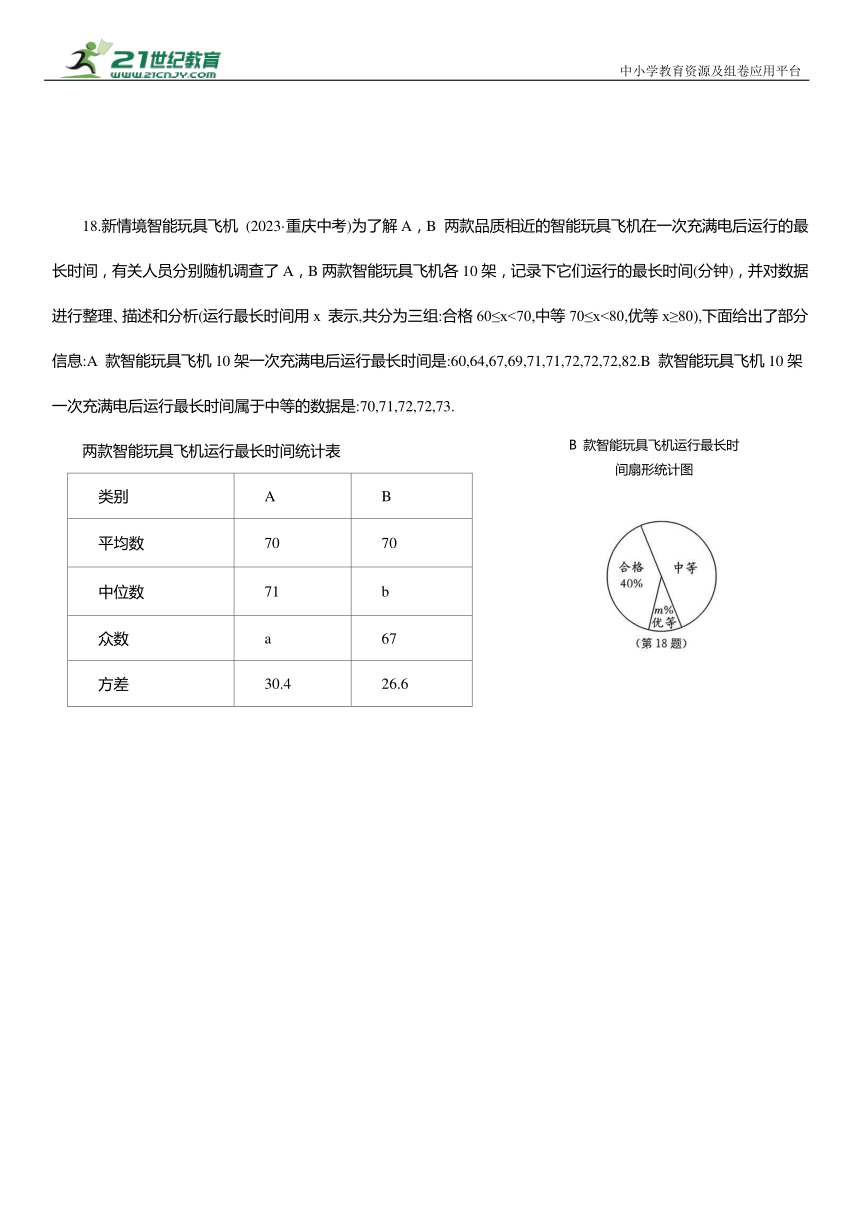
18.新情境智能玩具飞机 (2023·重庆中考)为了解A,B 两款品质相近的智能玩具飞机在一次充满电后运行的最长时间,有关人员分别随机调查了A,B两款智能玩具飞机各10架,记录下它们运行的最长时间(分钟),并对数据进行整理、描述和分析(运行最长时间用x 表示,共分为三组:合格60≤x<70,中等70≤x<80,优等x≥80),下面给出了部分信息:A 款智能玩具飞机10架一次充满电后运行最长时间是:60,64,67,69,71,71,72,72,72,82.B 款智能玩具飞机10架一次充满电后运行最长时间属于中等的数据是:70,71,72,72,73.
两款智能玩具飞机运行最长时间统计表
类别 A B
平均数 70 70
中位数 71 b
众数 a 67
方差 30.4 26.6
根据以上信息,解答下列问题:
(1)上述图表中a= ,b= ,m= .
(2)根据以上数据,你认为哪款智能玩具飞机运行性能更好 请说明理由(写出一条即可).
(3)若某玩具仓库有A 款智能玩具飞机200架、B 款智能玩具飞机 120架,估计两款智能玩具飞机运行性能在中等及以上的共有多少架
19.如图(1),有一张长40cm,宽20cm的长方形硬纸片,裁去角上2个小正方形和2个小长方形(图中阴影部分)之后,恰好折成如图(2)的有盖纸盒.
(1)若纸盒的高是3cm,求纸盒底面长方形的长和宽;
(2)若纸盒的底面积是150cm ,求纸盒的高.
20.(2024·山东济南历下区期末)
活动课题 风筝离地面垂直高度探究
问题 背景 风筝由中国古代劳动人民发明于东周春秋时期,距今已2000 多年,相传墨翟以木头制成木鸟,研制三年而成,是人类最早的风筝起源.兴趣小组在放风筝时想测量风筝离地面的垂直高度.
测量 数据 抽象 模型 小组成员测量了相关数据,并画出了如图所示的示意图,测得水平距离BC 的长为15米,根据手中剩余线的长度计算出风筝线 AB 的长为 17米,牵线放风筝的手到地面的距离为1.5米.
问题产生 经过讨论,兴趣小组得出以下问题: (1)运用所学勾股定理相关知识,根据测量所得数据,计算出风筝离地面的垂直高度. (2)如果想要风筝沿 DA 方向再上升12米,且BC 长度不变,则他应该再放出多少米线
问题解决 …
该报告还没有完成,请你帮助兴趣小组解决以上问题.
21.(2024·安徽芜湖无为月考)(1)如图(1),长方体的长为4cm,宽为3cm,高为12 cm.求该长方体中能放入木棒的最大长度.
(2)如图(2),长方体的长为4cm,宽为3cm,高为12cm.现有一只蚂蚁从点 A 处沿长方体的表面爬到点G处,求它爬行的最短路程.
(3)如图(3),若将题中的长方体换成透明圆柱形容器(容器厚度忽略不计)的高为12cm,底面周长为12cm,在容器内壁离底部5cm 的点 B 处有一饭粒,此时一只蚂蚁正好在容器外壁且离容器上沿 1 cm与饭粒相对的点 A处.求蚂蚁吃到饭粒需要爬行的最短路程是多少
1. B [解析] ∴电流 故电流I的值为5.故选 B.
2. C [解析]由题图可知,次数不低于42个的有两组,一组有8人,一组有6人,共14人.故选C.
3. C [解析]设小正方形的边长为x,大正方形的边长为y,则 则阴影部分的面积是( 故选 C.
思路引导 本题考查了二次根式的应用.解题的关键是把图中阴影部分看成是一个长方形,因此只要求出其长与宽的长度,即可求出阴影部分面积.
4. A [解析]设水的深度为 xm,则由题意可知竹竿长度为(x+0.5)m,由勾股定理,得( 1.5 ,展开,得 解得x=2.故选 A.
方法诠释根据题意可得将竹竿拉向岸边时,竹竿、水深、竹竿底端与岸边的距离构成一个直角三角形,且竹竿的长度相当于直角三角形的斜边,竹竿长度减去露出水面高度和竹竿底端到岸边距离相当于直角三角形的两个直角边.由勾股定理即可解答.
5. A [解析]设需要x个正三角形和y个正方形,列方程得60x+90y=360,得整数x=3,y=2.即至少要三个正三角形和两个正方形.故选 A.
6. D [解析]由统计表可知,从平均数看甲与丁两人相同,高于乙和丙;而从方差看丁和丙小于乙和甲.综合看丁的平均数最高,方差最小,即丁的成绩高且比较稳定.因此最合适的人选是丁.故选 D.
知识拓展方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
7. B [解析]设“阔”是x步,则长是(x+12)步,根据题意,得x(x+12)=864,整理得 解得 (不符合题意,舍去),. ,∴“阔”是24步.故选 B.
8. D [解析]设每轮传染中平均一个人传染了x个人,根据题意,得1+x+(x+1)x=225,解得x=14或x=-16(舍去),故每轮传染中平均一个人传染了14个人.故选 D.
思路引导 本题考查了一元二次方程的应用,解决本题的难点是分别表示第一轮传播后感染的人数以及第二轮感染的人数各是多少.
9. C [解析]①若蚂蚁从平面 ABCD 和平面CDFE 经过,蚂蚁到达饼干的最短距离如图(1),
②若蚂蚁从平面ABCD 和平面BCEI 经过,则蚂蚁到达饼干的最短距离如图(2),
∴最短距离为 故选C.
10. C [解析]①当AF 的长是12cm时,BC 的长是(80-12×4)÷4=8(cm),结论①正确;②假设这两个正方形的面积之和是 198 cm ,设 AF 的长为xcm,则BC的长为(80-4x)÷4=(20-x) cm,根据题意,得 整理,得. 2 ,∴原方程没有实数根,∴假设不成立,即这两个正方形的面积之和不能是198 cm ,结论②不正确;③假设这两个正方形的面积之和是288cm ,设AF的长为 ycm,则 BC 的长为(80-4y)÷4=(20-y) cm,根据题意,得 整理,得 解得 ∴符合题意,∴假设成立,即这两个正方形的面积之和可以是288cm ,结论③正确.∴正确的结论有2个.
故选C.
■思路引导 本题考查了一元二次方程的应用、根的判别式以及正方形的性质,找准等量关系,正确列出一元二次方程是解题的关键.
11.93.6 [解析]这学期的体育成绩=94×15%+90×35%+96×50%=93.6(分).
12.18° [解析]∵正五边形每个内角是 =108°,
13. [解析]由统计表可知,已知的四个数据中12出现了2次,13出现了1次,而13是唯一的众数,所以被覆盖的数据中至少有2个13,设另一个被覆盖的数为x,则11+12×2+13×3+x=12×7,解得x=10.所以方差
14.150米 [解析]由题意可知,小强第一次回到出发点时,其走过的路程是一个外角为24°的正多边形的周长,这个正多边形的边数为 所以走过的路程=15×10=150(米).
15.(1)2
(2) 或5 [解析](1)若四边形 PBQD 是平行四边形,则点 P 在AB 上,点 Q在DC上,如图(1),由题意,知BP=10-3t,DQ=2t,∴10-3t=2t,∴t=2.
(2)①当点 P 在线段AB 上时,即 时,如图(2),
②当点 P 在线段BC上时,即 时,如图(3),
∵BP=3t-10,CQ=16-2t,
2t)=15,∴t=5或 (舍).
故满足条件的t 的值为 或5.
思路引导 本题是四边形的综合题.(1)若四边形PBQD 是平行四边形,则点 P 在AB 上,点Q在DC上,则BP=10-3t,DQ=2t,根据平行四边形的性质可得10-3t=2t,解方程即可得到结论.
(2)分两种情况进行讨论:①当点 P 在线段AB 上时;②当点 P 在线段BC上时;根据三角形面积列方程计算即可.
16.从节约材料的角度考虑,应选择中号底面规格的纸箱.理由如下:
∵甲、乙两件礼品底面都是正方形,底面积分别为80cm ,180cm ,
∴甲礼品的底面边长为 乙礼品的底面边长为
∴小号包装纸箱长度尺寸不够,大号包装纸箱长度尺寸偏大,中号包装纸箱长、宽尺寸适中,∴从节约材料的角度考虑,应选择中号底面规格的纸箱.
思路引导 本题考查了二次根式的应用、正方形的面积、无理数的估算,理解题意得出要求包装纸箱的尺寸范围是解题的关键.
17.(1)设该公司投递快递总件数的月增长率为x,依题意,得
解得 (不符合题意,舍去).故该公司投递快递总件数的月增长率为30%.
(2)33.8×(1+30%)=43.94(万件).
∵43.94<45,
∴若该公司每月投递快递总件数的增长率保持不变,则5月份投递快递总件数不能达到45万件.
思路引导 (1)设该公司投递快递总件数的月增长率为x,利用该快递公司今年4月份投递快递总件数=该快递公司今年2月份投递快递总件数×(1+该公司投递快递总件数的月增长率) ,即可得出关于x的一元二次方程,解之取其正值即可得出结论;(2)利用该快递公司今年5月份投递快递总件数=该快递公司今年4月份投递快递总件数×(1+该公司投递快递总件数的月增长率),可求出该快递公司今年5月份投递快递总件数,再将其与45万件比较后即可得出结论.
18.(1)72 70.5 10 [解析]A款智能玩具飞机10架一次充满电后运行最长时间中,72 出现的次数最多,故众数a=72;把B 款智能玩具飞机10架一次充满电后运行最长时间从小到大排列,排在中间的两个数是70和71,故中位数 m%=1-50%-40%=10%,即m=10.
(2)A款智能玩具飞机运行性能更好,理由如下:虽然两款智能玩具飞机运行最长时间的平均数相同,但A 款智能玩具飞机运行最长时间的中位数和众数均高于B 款智能玩具飞机,所以A 款智能玩具飞机运行性能更好.(答案不唯一)
(架).故两款智能玩具飞机运行性能在中等及以上的大约共有192架.
19.(1)纸盒底面长方形的长为40÷2-3=17(cm),纸盒底面长方形的宽为20-2×3=14(cm).故纸盒底面长方形的长为17 cm,宽为14 cm.
(2)设当纸盒的高为 x cm时,纸盒的底面积是150cm ,由题意,得((20-x)(20-2x)=150,化简,得 解得
当x=5时,20-2x=10>0,符合题意;
当x=25时,20-2x=-30<0,不符合题意,舍去.
故若纸盒的底面积是150cm ,则纸盒的高为5cm.
20.(1)在 Rt△ABC 中,∠ACB=90°,BC=15 米,AB=17米,
由勾股定理,得 米,
∴AD=AC+CD=8+1.5=9.5(米).
故风筝离地面的垂直高度为9.5米.
(2)如图,当风筝沿 DA 方向再上升12米,A'C=20米,
在Rt△A'BC中,∠A'CB=90°,BC=15米,由勾股定理,
可得 米,
25-17=8(米).故他应该再放出8米长的线.
21.(1)如图(1),由题意,得该长方体中能放入木棒的最大长度是
(2)①如图(2), ②如图((3),
③如图((4),
∴最短路程为
(3)∵高为12cm,底面周长为12cm,在容器内壁离容器底部5cm 的点 B 处有一饭粒,此时蚂蚁正好在容器外壁,离容器上沿1cm与饭粒相对的点A 处,将容器沿侧面展开,作点 A 关于EF 的对称点A',如图(5),
∴A'D=6cm,BD=12--5+1=8(cm).
连接A'B,则A'B 即为最短距离,
思路引导 (1)利用勾股定理直接求出木棒的最大长度即可;(2)将长方体展开,利用勾股定理解答即可;(3)将容器侧面展开,作出点 A 关于EF 的对称点A′,根据两点之间线段最短可知A′B 的长度即为所求.
实际应用问题期末专题整合提优(四)
一、选择题
1.跨学科 导线问题 (2024·山东聊城阳谷期末)电流通过导线时会产生热量,电流I(单位:A)、导线电阻R(单位:Ω)、通电时间t(单位:s)与产生的热量Q(单位:J)满足 已知导线的电阻为2Ω,1s时间导线产生50J的热量,电流I 的值是( ).
A. 2 B. 5 C. 8 D. 10
2.某校随机抽查了八年级的30名女生,测试了1分钟仰卧起坐的次数,并绘制成如图的频数分布直方图(每组含前一个边界,不含后一个边界),则次数不低于42个的有( ).
A. 6名 B. 8名 C. 14名 D. 23名
3.(2024·安徽蚌埠期末)如图,长方形内有两个相邻的正方形,其面积分别为6 和24,则图中阴影部分面积为( ).
A. 5 B. 5 C. 6 D. 6
4.小刚准备测量一段河水的深度,他把一根竹竿插到离岸边1.5m远的水底,竹竿高出水面0.5m,把竹竿的顶端拉向岸边,竿顶和岸边的水面刚好相齐,则河水的深度为( ).
A. 2m B. 2. 5m C. 2.25 m D. 3m
5.如果要用正三角形和正方形两种图形进行密铺,那么至少需要( ).
A.三个正三角形和两个正方形
B.两个正三角形和三个正方形
C.两个正三角形和两个正方形
D.三个正三角形和三个正方形
6.(2024·盐城模拟)某校射击队从甲、乙、丙、丁四人中选拔一人参加市运会射击比赛.在选拔赛中,每人射击10次,他们 10 次成绩的平均数及方差如下表所示:
甲 乙 丙 丁
平均数/环 9.7 9.5 9.5 9.7
方差/环 5.1 4.7 4.5 4.5
请你根据表中数据选一人参加比赛,最合适的人选是( ).
A. 甲 B. 乙 C. 丙 D. 丁
7.传统文化 《田亩比类乘除捷法》(2024·安徽亳州期末)我国南宋数学家杨辉在1275年提出了一个问题:直田积(矩形面积)八百六十四步(平方步),只云阔(宽)不及长一十二步(宽比长少一十二步),则“阔”是( ).
A. 12步 B. 24步 C. 36步 D. 72步
8.(2024·安徽安庆期中)甲流病毒是一种传染性极强的急性呼吸道传染病,感染者的临床以发热、乏力、干咳为主要表现.在“甲流”初期,有1人感染了“甲流病毒”,如若得不到有效控制,经过两轮传染后共有225人感染了“甲流病毒”,则每轮传染中平均一个人传染了( ).
A. 11人 B. 12人 C. 13人 D. 14人
9.如图,长方体敞口玻璃罐的长、宽、高分别为16cm,6cm和6cm,在罐内点E 处有一小块饼干碎末,此时一只蚂蚁正好在罐外壁,在长方形 ABCD 中心的正上方2cm 的点 H 处,则蚂蚁到达饼干的最短距离是( ).
A. 24cm B. 18cm
10.(2024·天津河西区一模)把一根长为80cm的绳子剪成两段,并把每一段绳子都围成一个正方形,如图所示,有以下结论:
①当AF 的长是12cm时,BC 的长为8cm;
②这两个正方形的面积之和可以是198cm ;
③这两个正方形的面积之和可以是288cm .其中,正确结论的个数是().
A. 0 B. 1 C. 2 D. 3
二、填空题
11.某校规定学生的体育成绩由三部分组成,早晨锻炼及体育课外活动表现占成绩的15%,体育理论测试占35%,体育技能测试占50%,小明的上述三项成绩依次是94分,90分,96分,则小明这学期的体育成绩是 分.
12. 新情境 平面镶嵌 (2024·榆林高新区二模)某广场的地面是由相同的正五边形与相同的四角星形(四个尖角的度数相同)铺成的无缝隙、不重叠的图形,如图是该广场地面的一部分,则图中四角星形的尖角∠ABC 的度数为 .
13.为迎接期末体育测试,小强每天坚持引体向上锻炼,他记录了某一周每天做引体向上的个数,如下表:
星期 日 一 二 三 四 五 六
个数 11 12 13 12
其中有三天的个数被墨汁覆盖了,但小强已经计算出这组数据的唯一众数是13,平均数是12,那么这组数据的方差是 .
14.如图所示,小强从A 点出发,沿直线前进10米后左转 24°,再沿直线前进 10 米,又向左转24°,…,照这样走下去,他第一次回到出发地A 点时,一共走的路程是 .
15.中考新考法 动点问题(2024·安徽淮南田家庵区月考)如图,在四边形 ABCD 中,AB∥CD,∠BCD=90°,BC=8cm,AB=AD=10cm,点 P 从点A 出发,以每秒3c m 的速度沿折线A-B-C方向运动,点Q 从点 D 出发,以每秒2cm速度沿线段 DC 方向向点C运动.已知动点 P,Q 同时出发,当点 Q 运动到点C时,P,Q运动停止,设运动时间为t.
(1)当t= 秒时,四边形 PBQD 为平行四边形;
(2)在点 P,点Q 的运动过程中,当t = 秒时,△BPQ 的面积为15 cm .
三、解答题
16.新情境 方案选择 (2024·陕西安康旬阳期末)快递公司为顾客交寄的快递提供纸箱包装服务,现有三款包装纸箱,底面规格如下表:
型号 长 宽
小号 20cm 18cm
中号 25 cm 20cm
大号 30cm 25cm
已知甲、乙两件礼品底面都是正方形,底面积分别为80cm ,180cm 若要将它们合在一个包装箱中寄出,底面摆放方式如图,从节约材料的角度考虑,应选择哪种底面型号的纸箱 请说明理由.
乙的底面
甲的底面
(第16题)
17.(2024·泰州二中附中三模)我国快递行业迅速发展,经调查,某快递公司今年2月份投递快递总件数为 20万件,4月份投递快递总件数33.8万件,假设该公司每月投递快递总件数的增长率相同.
(1)求该公司投递快递总件数的月增长率.
(2)如果该公司每月投递快递总件数的增长率保持不变,那么5月份投递快递总件数是否达到45万件
18.新情境智能玩具飞机 (2023·重庆中考)为了解A,B 两款品质相近的智能玩具飞机在一次充满电后运行的最长时间,有关人员分别随机调查了A,B两款智能玩具飞机各10架,记录下它们运行的最长时间(分钟),并对数据进行整理、描述和分析(运行最长时间用x 表示,共分为三组:合格60≤x<70,中等70≤x<80,优等x≥80),下面给出了部分信息:A 款智能玩具飞机10架一次充满电后运行最长时间是:60,64,67,69,71,71,72,72,72,82.B 款智能玩具飞机10架一次充满电后运行最长时间属于中等的数据是:70,71,72,72,73.
两款智能玩具飞机运行最长时间统计表
类别 A B
平均数 70 70
中位数 71 b
众数 a 67
方差 30.4 26.6
根据以上信息,解答下列问题:
(1)上述图表中a= ,b= ,m= .
(2)根据以上数据,你认为哪款智能玩具飞机运行性能更好 请说明理由(写出一条即可).
(3)若某玩具仓库有A 款智能玩具飞机200架、B 款智能玩具飞机 120架,估计两款智能玩具飞机运行性能在中等及以上的共有多少架
19.如图(1),有一张长40cm,宽20cm的长方形硬纸片,裁去角上2个小正方形和2个小长方形(图中阴影部分)之后,恰好折成如图(2)的有盖纸盒.
(1)若纸盒的高是3cm,求纸盒底面长方形的长和宽;
(2)若纸盒的底面积是150cm ,求纸盒的高.
20.(2024·山东济南历下区期末)
活动课题 风筝离地面垂直高度探究
问题 背景 风筝由中国古代劳动人民发明于东周春秋时期,距今已2000 多年,相传墨翟以木头制成木鸟,研制三年而成,是人类最早的风筝起源.兴趣小组在放风筝时想测量风筝离地面的垂直高度.
测量 数据 抽象 模型 小组成员测量了相关数据,并画出了如图所示的示意图,测得水平距离BC 的长为15米,根据手中剩余线的长度计算出风筝线 AB 的长为 17米,牵线放风筝的手到地面的距离为1.5米.
问题产生 经过讨论,兴趣小组得出以下问题: (1)运用所学勾股定理相关知识,根据测量所得数据,计算出风筝离地面的垂直高度. (2)如果想要风筝沿 DA 方向再上升12米,且BC 长度不变,则他应该再放出多少米线
问题解决 …
该报告还没有完成,请你帮助兴趣小组解决以上问题.
21.(2024·安徽芜湖无为月考)(1)如图(1),长方体的长为4cm,宽为3cm,高为12 cm.求该长方体中能放入木棒的最大长度.
(2)如图(2),长方体的长为4cm,宽为3cm,高为12cm.现有一只蚂蚁从点 A 处沿长方体的表面爬到点G处,求它爬行的最短路程.
(3)如图(3),若将题中的长方体换成透明圆柱形容器(容器厚度忽略不计)的高为12cm,底面周长为12cm,在容器内壁离底部5cm 的点 B 处有一饭粒,此时一只蚂蚁正好在容器外壁且离容器上沿 1 cm与饭粒相对的点 A处.求蚂蚁吃到饭粒需要爬行的最短路程是多少
1. B [解析] ∴电流 故电流I的值为5.故选 B.
2. C [解析]由题图可知,次数不低于42个的有两组,一组有8人,一组有6人,共14人.故选C.
3. C [解析]设小正方形的边长为x,大正方形的边长为y,则 则阴影部分的面积是( 故选 C.
思路引导 本题考查了二次根式的应用.解题的关键是把图中阴影部分看成是一个长方形,因此只要求出其长与宽的长度,即可求出阴影部分面积.
4. A [解析]设水的深度为 xm,则由题意可知竹竿长度为(x+0.5)m,由勾股定理,得( 1.5 ,展开,得 解得x=2.故选 A.
方法诠释根据题意可得将竹竿拉向岸边时,竹竿、水深、竹竿底端与岸边的距离构成一个直角三角形,且竹竿的长度相当于直角三角形的斜边,竹竿长度减去露出水面高度和竹竿底端到岸边距离相当于直角三角形的两个直角边.由勾股定理即可解答.
5. A [解析]设需要x个正三角形和y个正方形,列方程得60x+90y=360,得整数x=3,y=2.即至少要三个正三角形和两个正方形.故选 A.
6. D [解析]由统计表可知,从平均数看甲与丁两人相同,高于乙和丙;而从方差看丁和丙小于乙和甲.综合看丁的平均数最高,方差最小,即丁的成绩高且比较稳定.因此最合适的人选是丁.故选 D.
知识拓展方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.
7. B [解析]设“阔”是x步,则长是(x+12)步,根据题意,得x(x+12)=864,整理得 解得 (不符合题意,舍去),. ,∴“阔”是24步.故选 B.
8. D [解析]设每轮传染中平均一个人传染了x个人,根据题意,得1+x+(x+1)x=225,解得x=14或x=-16(舍去),故每轮传染中平均一个人传染了14个人.故选 D.
思路引导 本题考查了一元二次方程的应用,解决本题的难点是分别表示第一轮传播后感染的人数以及第二轮感染的人数各是多少.
9. C [解析]①若蚂蚁从平面 ABCD 和平面CDFE 经过,蚂蚁到达饼干的最短距离如图(1),
②若蚂蚁从平面ABCD 和平面BCEI 经过,则蚂蚁到达饼干的最短距离如图(2),
∴最短距离为 故选C.
10. C [解析]①当AF 的长是12cm时,BC 的长是(80-12×4)÷4=8(cm),结论①正确;②假设这两个正方形的面积之和是 198 cm ,设 AF 的长为xcm,则BC的长为(80-4x)÷4=(20-x) cm,根据题意,得 整理,得. 2 ,∴原方程没有实数根,∴假设不成立,即这两个正方形的面积之和不能是198 cm ,结论②不正确;③假设这两个正方形的面积之和是288cm ,设AF的长为 ycm,则 BC 的长为(80-4y)÷4=(20-y) cm,根据题意,得 整理,得 解得 ∴符合题意,∴假设成立,即这两个正方形的面积之和可以是288cm ,结论③正确.∴正确的结论有2个.
故选C.
■思路引导 本题考查了一元二次方程的应用、根的判别式以及正方形的性质,找准等量关系,正确列出一元二次方程是解题的关键.
11.93.6 [解析]这学期的体育成绩=94×15%+90×35%+96×50%=93.6(分).
12.18° [解析]∵正五边形每个内角是 =108°,
13. [解析]由统计表可知,已知的四个数据中12出现了2次,13出现了1次,而13是唯一的众数,所以被覆盖的数据中至少有2个13,设另一个被覆盖的数为x,则11+12×2+13×3+x=12×7,解得x=10.所以方差
14.150米 [解析]由题意可知,小强第一次回到出发点时,其走过的路程是一个外角为24°的正多边形的周长,这个正多边形的边数为 所以走过的路程=15×10=150(米).
15.(1)2
(2) 或5 [解析](1)若四边形 PBQD 是平行四边形,则点 P 在AB 上,点 Q在DC上,如图(1),由题意,知BP=10-3t,DQ=2t,∴10-3t=2t,∴t=2.
(2)①当点 P 在线段AB 上时,即 时,如图(2),
②当点 P 在线段BC上时,即 时,如图(3),
∵BP=3t-10,CQ=16-2t,
2t)=15,∴t=5或 (舍).
故满足条件的t 的值为 或5.
思路引导 本题是四边形的综合题.(1)若四边形PBQD 是平行四边形,则点 P 在AB 上,点Q在DC上,则BP=10-3t,DQ=2t,根据平行四边形的性质可得10-3t=2t,解方程即可得到结论.
(2)分两种情况进行讨论:①当点 P 在线段AB 上时;②当点 P 在线段BC上时;根据三角形面积列方程计算即可.
16.从节约材料的角度考虑,应选择中号底面规格的纸箱.理由如下:
∵甲、乙两件礼品底面都是正方形,底面积分别为80cm ,180cm ,
∴甲礼品的底面边长为 乙礼品的底面边长为
∴小号包装纸箱长度尺寸不够,大号包装纸箱长度尺寸偏大,中号包装纸箱长、宽尺寸适中,∴从节约材料的角度考虑,应选择中号底面规格的纸箱.
思路引导 本题考查了二次根式的应用、正方形的面积、无理数的估算,理解题意得出要求包装纸箱的尺寸范围是解题的关键.
17.(1)设该公司投递快递总件数的月增长率为x,依题意,得
解得 (不符合题意,舍去).故该公司投递快递总件数的月增长率为30%.
(2)33.8×(1+30%)=43.94(万件).
∵43.94<45,
∴若该公司每月投递快递总件数的增长率保持不变,则5月份投递快递总件数不能达到45万件.
思路引导 (1)设该公司投递快递总件数的月增长率为x,利用该快递公司今年4月份投递快递总件数=该快递公司今年2月份投递快递总件数×(1+该公司投递快递总件数的月增长率) ,即可得出关于x的一元二次方程,解之取其正值即可得出结论;(2)利用该快递公司今年5月份投递快递总件数=该快递公司今年4月份投递快递总件数×(1+该公司投递快递总件数的月增长率),可求出该快递公司今年5月份投递快递总件数,再将其与45万件比较后即可得出结论.
18.(1)72 70.5 10 [解析]A款智能玩具飞机10架一次充满电后运行最长时间中,72 出现的次数最多,故众数a=72;把B 款智能玩具飞机10架一次充满电后运行最长时间从小到大排列,排在中间的两个数是70和71,故中位数 m%=1-50%-40%=10%,即m=10.
(2)A款智能玩具飞机运行性能更好,理由如下:虽然两款智能玩具飞机运行最长时间的平均数相同,但A 款智能玩具飞机运行最长时间的中位数和众数均高于B 款智能玩具飞机,所以A 款智能玩具飞机运行性能更好.(答案不唯一)
(架).故两款智能玩具飞机运行性能在中等及以上的大约共有192架.
19.(1)纸盒底面长方形的长为40÷2-3=17(cm),纸盒底面长方形的宽为20-2×3=14(cm).故纸盒底面长方形的长为17 cm,宽为14 cm.
(2)设当纸盒的高为 x cm时,纸盒的底面积是150cm ,由题意,得((20-x)(20-2x)=150,化简,得 解得
当x=5时,20-2x=10>0,符合题意;
当x=25时,20-2x=-30<0,不符合题意,舍去.
故若纸盒的底面积是150cm ,则纸盒的高为5cm.
20.(1)在 Rt△ABC 中,∠ACB=90°,BC=15 米,AB=17米,
由勾股定理,得 米,
∴AD=AC+CD=8+1.5=9.5(米).
故风筝离地面的垂直高度为9.5米.
(2)如图,当风筝沿 DA 方向再上升12米,A'C=20米,
在Rt△A'BC中,∠A'CB=90°,BC=15米,由勾股定理,
可得 米,
25-17=8(米).故他应该再放出8米长的线.
21.(1)如图(1),由题意,得该长方体中能放入木棒的最大长度是
(2)①如图(2), ②如图((3),
③如图((4),
∴最短路程为
(3)∵高为12cm,底面周长为12cm,在容器内壁离容器底部5cm 的点 B 处有一饭粒,此时蚂蚁正好在容器外壁,离容器上沿1cm与饭粒相对的点A 处,将容器沿侧面展开,作点 A 关于EF 的对称点A',如图(5),
∴A'D=6cm,BD=12--5+1=8(cm).
连接A'B,则A'B 即为最短距离,
思路引导 (1)利用勾股定理直接求出木棒的最大长度即可;(2)将长方体展开,利用勾股定理解答即可;(3)将容器侧面展开,作出点 A 关于EF 的对称点A′,根据两点之间线段最短可知A′B 的长度即为所求.
