18.1 勾股定理 提优训练 (含答案)
文档属性
| 名称 | 18.1 勾股定理 提优训练 (含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 451.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-16 00:00:00 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
18.1 勾股定理
第1课时 勾股定理(1)
基础巩固提优
1.若一个直角三角形的两直角边长分别是5 和12,则斜边长为( ).
A. 13
C. 7或17 D. 13或
2.如图,点A 在数轴上,其表示的数为2,过点A 作AB⊥OA,且AB=3.以点O为圆心,OB 为半径作弧,与数轴正半轴交于点 P,则点 P 表示的实数为( ).
A. B. 3.6 D. 4
3.先观察图形(如图所示),然后回答问题:
(1)设每个小方格的边长是1,则小正方形 M的面积是 ,小正方形 N 的面积是 ,正方形 S 的面积是 .
(2)正方形 M,正方形 N,正方形 S 的面积之间有何关系 你能发现AB,AC,BC 之间的关系吗
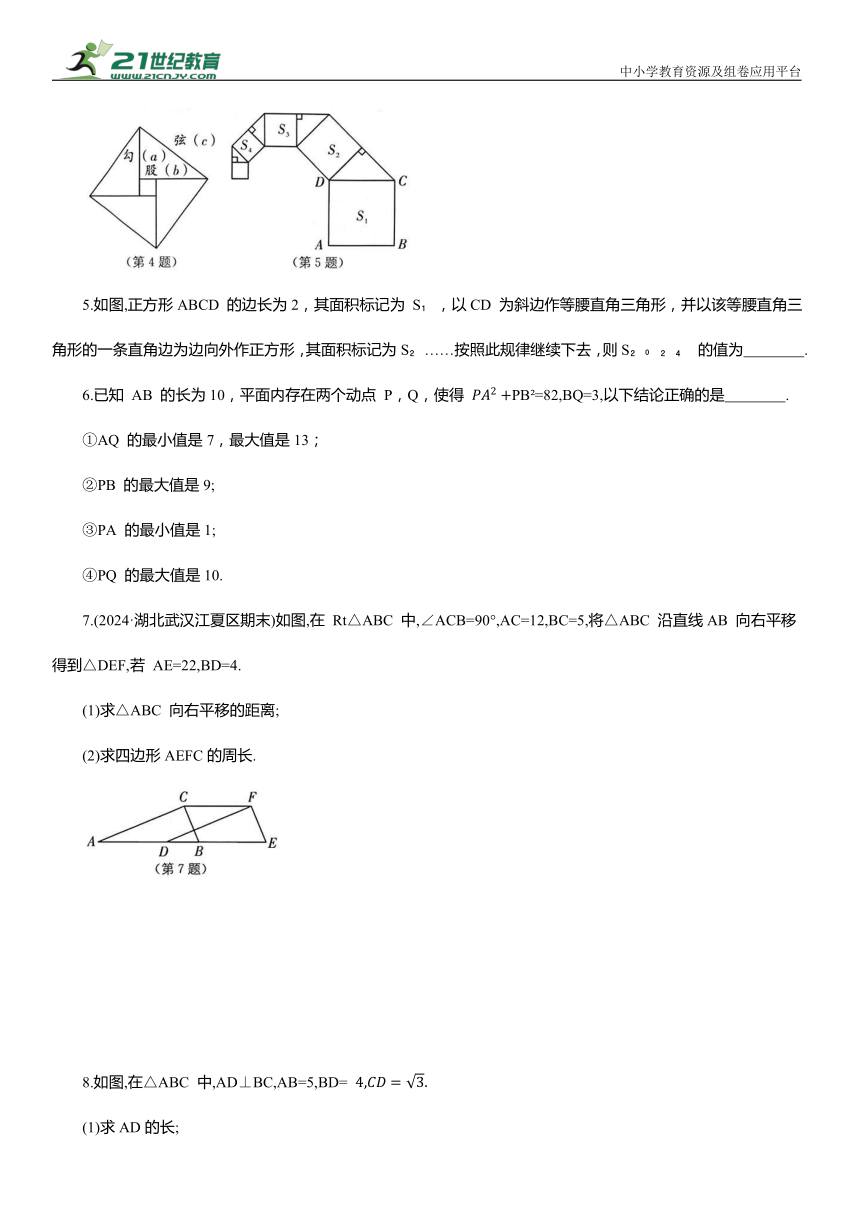
4.我国汉代数学家赵爽证明勾股定理时创制了一幅“勾股圆方图”,后人称之为“赵爽弦图”,它是由 4个全等的直角三角形和一个小正方形组成.如图,直角三角形的直角边长为a,b,斜边长为c,若b--a=4,c=20,则每个直角三角形的面积为 .
5.如图,正方形ABCD 的边长为2,其面积标记为 S ,以CD 为斜边作等腰直角三角形,并以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S ……按照此规律继续下去,则S 的值为 .
6.已知 AB 的长为10,平面内存在两个动点 P,Q,使得 PB =82,BQ=3,以下结论正确的是 .
①AQ 的最小值是7,最大值是13;
②PB 的最大值是9;
③PA 的最小值是1;
④PQ 的最大值是10.
7.(2024·湖北武汉江夏区期末)如图,在 Rt△ABC 中,∠ACB=90°,AC=12,BC=5,将△ABC 沿直线AB 向右平移得到△DEF,若 AE=22,BD=4.
(1)求△ABC 向右平移的距离;
(2)求四边形AEFC的周长.
8.如图,在△ABC 中,AD⊥BC,AB=5,BD=
(1)求AD的长;
(2)求△ABC 的周长.
9.如图,网格中的小正方形边长均为1,△ABC 的三个顶点均在格点上,完成下列问题:
(1)AB= ;BC= ;AC= ;
(2)求△ABC 的面积;
(3)求 AB 边上的高.
10.如图,等腰三角形ABC 的底边 BC 的长为8cm,腰AB的长为5cm,一动点 P 在底边上从点 B 向点C 以0.25 cm/s的速度运动.请你探究:当点 P 运动几秒时,点P 与顶点A 的连线PA与腰垂直
11.如图,在 Rt△ABC 中,∠C=90°,∠B=30°,BC=6,AD 平分∠CAB 交BC 于点 D,点 E 为边 AB 上一点,则线段DE长度的最小值为( ).
A. B. C. 2 D. 3
(2024·陕西中考)如图,在△ABC 中,AB=AC,E 是边AB 上一点,连接CE,在 BC 的右侧作BF∥AC,且 BF=AE,连接CF.若 AC=13,BC=10,则四边形 EBFC 的面积为 .
第2课时 勾 股 定 理(2)
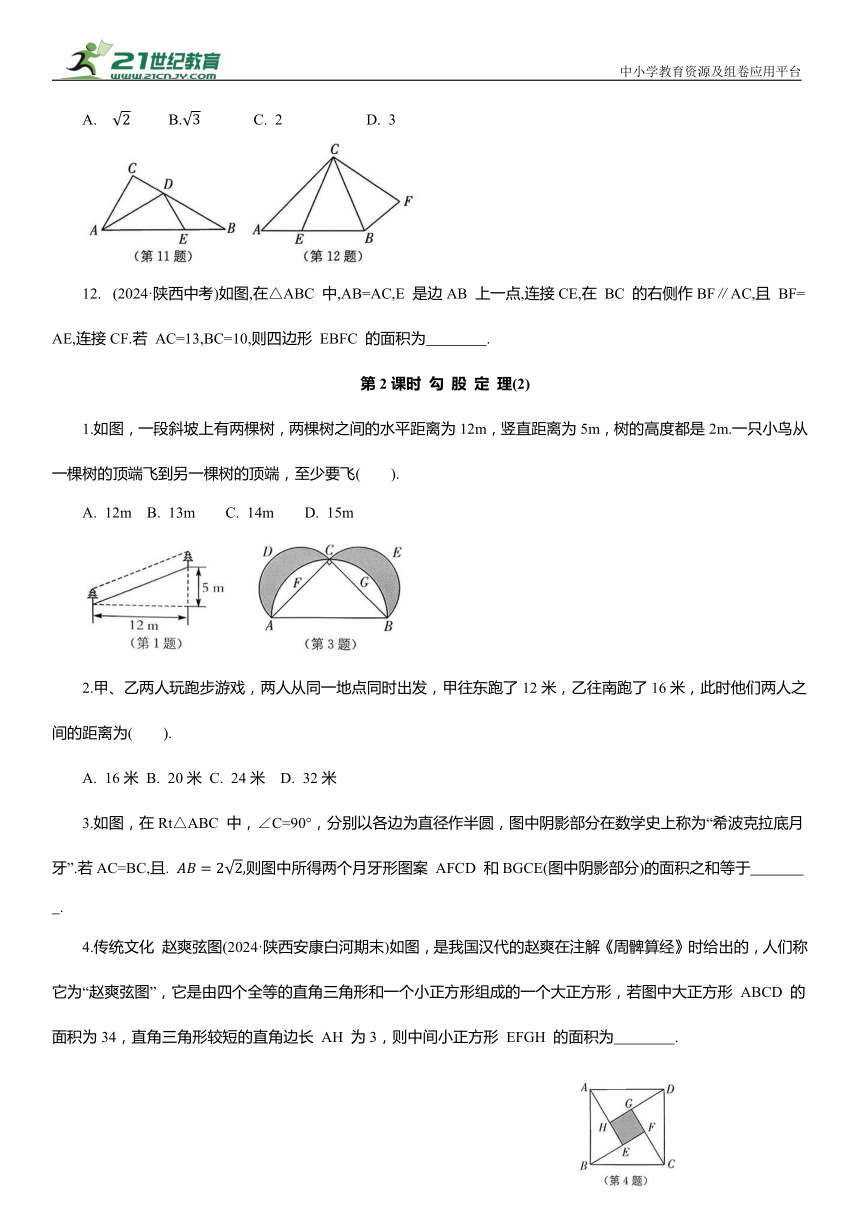
1.如图,一段斜坡上有两棵树,两棵树之间的水平距离为12m,竖直距离为5m,树的高度都是2m.一只小鸟从一棵树的顶端飞到另一棵树的顶端,至少要飞( ).
A. 12m B. 13m C. 14m D. 15m
2.甲、乙两人玩跑步游戏,两人从同一地点同时出发,甲往东跑了12米,乙往南跑了16米,此时他们两人之间的距离为( ).
A. 16米 B. 20米 C. 24米 D. 32米
3.如图,在Rt△ABC 中,∠C=90°,分别以各边为直径作半圆,图中阴影部分在数学史上称为“希波克拉底月牙”.若AC=BC,且. 则图中所得两个月牙形图案 AFCD 和BGCE(图中阴影部分)的面积之和等于 .
4.传统文化 赵爽弦图(2024·陕西安康白河期末)如图,是我国汉代的赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”,它是由四个全等的直角三角形和一个小正方形组成的一个大正方形,若图中大正方形 ABCD 的面积为34,直角三角形较短的直角边长 AH 为3,则中间小正方形 EFGH 的面积为 .
5. 如图,在某山峰上适当的位置找一点 A 修建索道口,经测量A 的垂直高度AC=600米,在山下点 B 处也修建一个索道口,BC=1 200米,从山下索道口坐缆车到山顶,已知缆车每分钟走120米,那么大约多少分钟后才能达到山顶 ,结果精确到0.1米)
思维拓展提优
6. 图(1)是第七届国际数学教育大会(ICME-7)的会徽图案,它是由一串有公共顶点O 的直角三角形(如图(2)所示)演化而成的.如果图(2)中的 那么OA 的长为( ).
A. 2 B. 3
7.如图,圆柱形容器中,高为1.2m,底面周长为1m,在容器内壁离容器底部0.3m的点 B 处有一蚊子,此时一只壁虎正好在容器外壁,离容器上沿0.3m与蚊子相对的点 A 处,则壁虎捕捉蚊子的最短距离为 m(容器厚度忽略不计).
8.如图,母子两猴在树上的点 A 处戏耍,在距离树的底部B 的20m处有一水池C,它们准备到池里喝水,母猴从树上爬下走到池边,小猴则爬高 5m 到树的顶端 D 处直接跃入池中,跃入池中的路线可看作是线段 DC.如果两猴经过的路程相同,求树高 BD.
9.如图,梯子斜靠在竖直的墙AO上,AO长为24dm,OB 为7 dm.
(1)求梯子AB 的长;
(2)梯子的顶端A 沿墙下滑4d m到点 C,梯子底端 B 外移到点D,求BD 的长.
10.有一个如图的长方体透明玻璃鱼缸,假设其长AD=80cm,高AB=60cm,水深AE=40cm,在水面上紧贴内壁的点 G 处有一块面包屑,G 在水面线EF 上,且EG=60cm,一只蚂蚁想从鱼缸外的点 A 沿鱼缸壁爬进鱼缸内的G处吃面包屑.
(1)该蚂蚁应该沿怎样的路线爬行才能使路程最短呢 请你画出它爬行的路线,并用箭头标注.
(2)求蚂蚁爬行的最短路线长.
11.传统文化《周髀算经》 (2024·西安莲湖区模拟)如图所示的图案是我国汉代数学家赵爽在注解《周髀算经》中“赵爽弦图”经修饰后的图形,四边形 ABCD 与四边形EFGH 均为正方形,H是 DE 的中点,阴影部分的面积为27,则AD 的长为 .
12. [问题情境]
勾股定理是一条古老的数学定理,它有很多种证明方法,我国汉代数学家赵爽根据弦图,利用面积法进行证明,著名数学家华罗庚曾提出把“数形关系”(勾股定理)带到其他星球,作为地球人与其他星球“人”进行第一次“谈话”的语言.
[定理表述]
请你根据图(1)中的直角三角形叙述勾股定理;(用文字及符号语言叙述)
[尝试证明]
以图(1)中的直角三角形为基础,可以构造出以a,b为底,以a+b为高的直角梯形(如图(2)),请你利用图(2),验证勾股定理;
[知识拓展]
利用图(2)中的直角梯形,我们可以证明 其证明步骤如下:
∵BC=a+b,AD= ,又在直角梯形 ABCD 中,BC (填大小关系)AD,即 ,
中考提分新题
13.如图(1)是北京国际数学家大会的会标,它取材于我国古代数学家赵爽的“弦图”,是由四个全等的直角三角形拼成.若图(1)中大正方形的面积为24,小正方形的面积为4,现将这四个直角三角形拼成图(2),则图(2)中大正方形的面积为( ).
A. 24 B. 36
C. 40 D. 44
14.数学文化 “毕达哥拉斯树” (2024·大庆中考)如图(1),直角三角形的两个锐角分别是 40°和50°,其三边上分别有一个正方形.执行下面的操作:由两个小正方形向外分别作锐角为40°和50°的直角三角形,再分别以所得到的直角三角形的直角边为边长作正方形.图(2)是1次操作后的图形.图(3)是重复上述步骤若干次后得到的图形,人们把它称为“毕达哥拉斯树”.若图(1)中的直角三角形斜边长为2,则10次操作后图形中所有正方形的面积和为 .
18.1 勾 股 定 理
第1课时 勾 股 定理(1)
1. A [解析]根据勾股定理,得斜边长为 13.故选 A.
2. C [解析]由勾股定理,得
∵以点O为圆心,OB 为半径作弧,与数轴正半轴交于点 P, ∴点 P 表示的实数为 故选C.
3.(1)1 1 2
(2)正方形 M 的面积+正方形 N 的面积=正方形S的面积.
思路引导本题考查正方形面积计算和勾股定理.
(1)由正方形面积公式可知:每个小正方形的面积等于边长的平方,即小正方形M 和小正方形N 的面积都等于1;而正方形S的面积等于4个小方格面积的一半,即等于两个小方格的面积,等于2;(2)由图示可知,BC是直角三角形ABC的斜边,由勾股定理可知
4.96 [解析]由图可得,
∴每个直角三角形的面积为
[解析]如图.由题意,得第一个正方形的边长为2,则
∵△DEC 是等腰直角三角形,
∴第二个正方形的边长为
∵△FGH 是等腰直角三角形,∴第三个正方形的边长为
同理可得,第四个正方形的边长为
∴第n个正方形的边长为
■归纳总结 本题考查图形类规律、等腰直角三角形的性质、勾股定理,掌握勾股定理得到第n个正方形的边长是关键.
6.①②③ [解析]如图,取AB 中点D,连接PD.过点 P作PM⊥AB,以点 B 为圆心,以 BQ 为半径作⊙B,QQ'为⊙B 直径.
∴设AD=DB=a,设DM=b,则MB=a-b.
2
又
①如图,AQ 最小=AB--BQ=10--3=7,AQ'最大 .故①正确;
②如图,PB≤PD+DB,∴PB 最大=PD+DB=4+5=9.故②正确;
③如图,PA≥AD-PD,∴PA 最小=AD-PD=5--4=1.故③正确;
④如图,PQ'≤PD+DB+BQ',∴PQ'最大=PD+ 故④错误.
综上所述,正确的是①②③.
思路引导本题考查了勾股定理,作垂线构造直角三角形是解题的关键.
7.(1)在Rt△ABC中,∠ACB=90°,AC=12,BC=5,由勾股定理,得 ∵AE=22,∴BE=22-13=9,则△ABC 向右平移的距离为9.
(2)由平移的性质可知,CF=BE=9,EF=BC=5,∴四边形AEFC 的周长=AC+AE+EF+CF=12+22+5+9=48.
解后反思 本题考查的是勾股定理、平移的性质,掌握平移的性质和勾股定理是解题的关键.
8.(1)在 Rt△ABD中,AB=5,BD=4,
由勾股定理,得
(2)在Rt△ACD中,
由勾股定理,得 所以△ABC 的周长=AB+BD+CD+AC=
(2)△ABC的面积
(3)△ABC的面积 边上的高,即AB边上的高
关键提醒 本题考查了勾股定理与网格、等积法,掌握勾股定理和利用等积法求AB 边上的高是解题的关键.
10.如图,过点 A 作AD⊥BC,垂足为D.
由等腰三角形的性质知, ∴在 Rt△ADB 中,
①当PA⊥AC时,设BP= xcm,则PD=(4-x) cm,PC=(8-x) cm.
在 Rt△PAD中,
在Rt△PAC 中,
解得x=1.75,即BP=1.75cm.
∴点 P 运动的时间为1.75÷0.25=7(s).
②当PA⊥AB 时,
同理可得PC=1.75cm,
∴BP=8-1.75=6.25(cm).
此时点 P 运动的时间为6.25÷0.25=25(s).
综上所述,当点 P 运动7 s 或25 s时,PA 与腰垂直.
方法总结 本题根据等腰三角形腰的两种情况进行分类讨论,根据勾股定理构建方程,进行运算求解.
11. C [解析]在Rt△ABC中,设AC=x.
∵∠B=30°,∴AB=2x,∠ACB=90°.
由勾股定理,得 解得
在Rt△ACD 中, 设CD=y,则AD=2y,由勾股定理,得 解得y=2(y>0),∴CD=2.
∵AD平分∠CAB,且DC⊥AC,∴点 D 到AB 边的距离等于线段CD 的长,即线段 DE 长度的最小值为2.
■归纳总结 本题考查勾股定理、垂线段最短及含30度角的直角三角形,熟知角平分线的性质及勾股定理是解题的关键.
12.60 [解析]∵AB=AC,∴∠ABC=∠ACB.
∵BF∥AC,∴∠ACB=∠CBF,
∴∠ABC=∠CBF,∴BC平分∠ABF.
如图,过点 C作CM⊥
AB,CN⊥BF,
则CM=CN.
(
CN,且BF=AE,∴S△ACE=S△CBF,
∴四边形EBFC 的面积
∵AC=13,∴AB=13.
设AM=x,则BM=13-x,
由勾股定理,得
解得
∴四边形 EBFC的面积为60.
■ 关键提醒 本题考查了勾股定理、等腰三角形的性质,将四边形EBFC的面积先转化为 再转化为 S△CBA 是解题的关键.
第2课时 勾 股 定 理 (2)
1. B [解析]如图.根据题意,得∠ABC=90°,AB=12m,BC=5m,
故一只小鸟从一棵树的顶端飞到另一棵树的顶端,至少要飞13m.故选 B.
2. B [解析]根据方位角可知两人所走的方向正好构成了直角.根据勾股定理,得他们两人之间的距离为 (米).故选 B.
解后反思 本题考查的是勾股定理的应用,根据题意判断直角三角形是解答本题的关键.
3.2 [解析]∵ ∴AC=BC=2,
4.4 [解析]∵题图中大正方形 ABCD 的面积为34,直角三角形较短的直角边长 AH 为3,
由勾股定理,得 即 (负值舍去),
∴中间小正方形 EFGH 的面积为(
5.由勾股定理,得
(米),
∴到达山顶需要的时间是1344÷120=11.2(分钟).故大约11.2分钟后才能达到山顶.
6. A [解析]· 由勾股定理,得 同理, 故选 A.
7.1.3 [解析]如图,将容器侧面的一半展开,作A 关于EF 的对称点A',∵高为1.2m,底面周长为1m,在容器内壁离容器底部0.3m的点 B 处有一蚊子,此时一只壁虎正好在容器外壁,离容器上沿0.3m与蚊子相对的点A处,∴A'D=0.5m,BD=1.2-0.3+AE=1.2m.在 Rt△A'BD中, 故壁虎捕捉蚊子的最短距离为1.3m.
8.设AB= xm,则BD=(x+5)m.
由AD+DC=AB+BC,得
5+DC=x+20,∴DC=(x+15)m.
在Rt△DBC中,由勾股定理,得 即 解得x=10.
∴BD=x+5=15m.故树高 BD 为15m.
9.(1)由题意可知,∠AOB=90°,AO=24 dm,OB=7 dm,. 故梯子AB的长为25dm.
(2)由题意可知,CD=AB=25dm,AC=4dm,∴OC=AO-AC=24-4=20(dm).
在 Rt△COD 中,由勾股定理,得
∴BD=OD-OB=15-7=8(dm).
故BD 的长为8dm.
10.(1)如图,作点 A 关于BC 的对称点A',连接A'G交BC 于点Q,则蚂蚁沿着A→Q→G的路线爬行时,路程最短.
(2)如图,在 Rt△A'EG 中,A'E=2AB-AE=80cm,EG=60cm,
100 cm.∴蚂蚁爬行的最短路线长为100 cm.
11.3 [解析]由四边形 ABCD 与四边形EFGH 均为正方形,H 是 DE 的中点,可知 E,F,G 分别为AF,BG,CH 的中点,且 AE=EH =DH=HG=CG=FG=BF=EF,
∴EH=AE=3,∴DE=2EH=6.
又
■解后反思 本题考查了直角三角形的性质、勾股定理的证明,找到周围三角形面积和中间正方形面积的关系是解题的关键.
12.[定理表述]
如果直角三角形的两直角边长分别为a,b,斜边长为c,那么
[尝试证明]
∵Rt△ABE≌Rt△ECD,∴∠AEB=∠EDC.
又∠EDC+∠DEC=90°,∴∠AEB+∠DEC=90°,
∴∠AED=90°.
整理,得
[知识拓展]
■方法总结 本题根据全等三角形的性质、面积分割法、勾股定理等知识,证明相关问题.
13. D [解析]如图,直角三角形的两直角边为a,b,斜边为c,
∵图(1)中大正方形的面积是24,
∵小正方形的面积是4,. 2ab=4,∴ab=10,
∴图(2)中最大的正方形的面积为 24+2×10=44.
14.48 [解析]根据勾股定理易得,题图(1)中所有正方形的面积和为8,那么经过1次操作后增加的4个小正方形的面积的和为4,那么经过1次操作后所有正方形的面积和为8+4,同理可得经过2次操作后增加的8个小正方形的面积的和也为4,那么经过2次操作后所有正方形的面积和为8+2×4,那么可推断10次操作后所有正方形的面积和为8+10×4=8+40=48.
难难度突破 本题考查勾股定理的相关知识.根据勾股定理得到以直角三角形各边长为边长的正方形的面积之间的关系是解决本题的关键;难点是得到n次操作后,所有正方形的面积的和等于8+4n.
18.1 勾股定理
第1课时 勾股定理(1)
基础巩固提优
1.若一个直角三角形的两直角边长分别是5 和12,则斜边长为( ).
A. 13
C. 7或17 D. 13或
2.如图,点A 在数轴上,其表示的数为2,过点A 作AB⊥OA,且AB=3.以点O为圆心,OB 为半径作弧,与数轴正半轴交于点 P,则点 P 表示的实数为( ).
A. B. 3.6 D. 4
3.先观察图形(如图所示),然后回答问题:
(1)设每个小方格的边长是1,则小正方形 M的面积是 ,小正方形 N 的面积是 ,正方形 S 的面积是 .
(2)正方形 M,正方形 N,正方形 S 的面积之间有何关系 你能发现AB,AC,BC 之间的关系吗
4.我国汉代数学家赵爽证明勾股定理时创制了一幅“勾股圆方图”,后人称之为“赵爽弦图”,它是由 4个全等的直角三角形和一个小正方形组成.如图,直角三角形的直角边长为a,b,斜边长为c,若b--a=4,c=20,则每个直角三角形的面积为 .
5.如图,正方形ABCD 的边长为2,其面积标记为 S ,以CD 为斜边作等腰直角三角形,并以该等腰直角三角形的一条直角边为边向外作正方形,其面积标记为S ……按照此规律继续下去,则S 的值为 .
6.已知 AB 的长为10,平面内存在两个动点 P,Q,使得 PB =82,BQ=3,以下结论正确的是 .
①AQ 的最小值是7,最大值是13;
②PB 的最大值是9;
③PA 的最小值是1;
④PQ 的最大值是10.
7.(2024·湖北武汉江夏区期末)如图,在 Rt△ABC 中,∠ACB=90°,AC=12,BC=5,将△ABC 沿直线AB 向右平移得到△DEF,若 AE=22,BD=4.
(1)求△ABC 向右平移的距离;
(2)求四边形AEFC的周长.
8.如图,在△ABC 中,AD⊥BC,AB=5,BD=
(1)求AD的长;
(2)求△ABC 的周长.
9.如图,网格中的小正方形边长均为1,△ABC 的三个顶点均在格点上,完成下列问题:
(1)AB= ;BC= ;AC= ;
(2)求△ABC 的面积;
(3)求 AB 边上的高.
10.如图,等腰三角形ABC 的底边 BC 的长为8cm,腰AB的长为5cm,一动点 P 在底边上从点 B 向点C 以0.25 cm/s的速度运动.请你探究:当点 P 运动几秒时,点P 与顶点A 的连线PA与腰垂直
11.如图,在 Rt△ABC 中,∠C=90°,∠B=30°,BC=6,AD 平分∠CAB 交BC 于点 D,点 E 为边 AB 上一点,则线段DE长度的最小值为( ).
A. B. C. 2 D. 3
(2024·陕西中考)如图,在△ABC 中,AB=AC,E 是边AB 上一点,连接CE,在 BC 的右侧作BF∥AC,且 BF=AE,连接CF.若 AC=13,BC=10,则四边形 EBFC 的面积为 .
第2课时 勾 股 定 理(2)
1.如图,一段斜坡上有两棵树,两棵树之间的水平距离为12m,竖直距离为5m,树的高度都是2m.一只小鸟从一棵树的顶端飞到另一棵树的顶端,至少要飞( ).
A. 12m B. 13m C. 14m D. 15m
2.甲、乙两人玩跑步游戏,两人从同一地点同时出发,甲往东跑了12米,乙往南跑了16米,此时他们两人之间的距离为( ).
A. 16米 B. 20米 C. 24米 D. 32米
3.如图,在Rt△ABC 中,∠C=90°,分别以各边为直径作半圆,图中阴影部分在数学史上称为“希波克拉底月牙”.若AC=BC,且. 则图中所得两个月牙形图案 AFCD 和BGCE(图中阴影部分)的面积之和等于 .
4.传统文化 赵爽弦图(2024·陕西安康白河期末)如图,是我国汉代的赵爽在注解《周髀算经》时给出的,人们称它为“赵爽弦图”,它是由四个全等的直角三角形和一个小正方形组成的一个大正方形,若图中大正方形 ABCD 的面积为34,直角三角形较短的直角边长 AH 为3,则中间小正方形 EFGH 的面积为 .
5. 如图,在某山峰上适当的位置找一点 A 修建索道口,经测量A 的垂直高度AC=600米,在山下点 B 处也修建一个索道口,BC=1 200米,从山下索道口坐缆车到山顶,已知缆车每分钟走120米,那么大约多少分钟后才能达到山顶 ,结果精确到0.1米)
思维拓展提优
6. 图(1)是第七届国际数学教育大会(ICME-7)的会徽图案,它是由一串有公共顶点O 的直角三角形(如图(2)所示)演化而成的.如果图(2)中的 那么OA 的长为( ).
A. 2 B. 3
7.如图,圆柱形容器中,高为1.2m,底面周长为1m,在容器内壁离容器底部0.3m的点 B 处有一蚊子,此时一只壁虎正好在容器外壁,离容器上沿0.3m与蚊子相对的点 A 处,则壁虎捕捉蚊子的最短距离为 m(容器厚度忽略不计).
8.如图,母子两猴在树上的点 A 处戏耍,在距离树的底部B 的20m处有一水池C,它们准备到池里喝水,母猴从树上爬下走到池边,小猴则爬高 5m 到树的顶端 D 处直接跃入池中,跃入池中的路线可看作是线段 DC.如果两猴经过的路程相同,求树高 BD.
9.如图,梯子斜靠在竖直的墙AO上,AO长为24dm,OB 为7 dm.
(1)求梯子AB 的长;
(2)梯子的顶端A 沿墙下滑4d m到点 C,梯子底端 B 外移到点D,求BD 的长.
10.有一个如图的长方体透明玻璃鱼缸,假设其长AD=80cm,高AB=60cm,水深AE=40cm,在水面上紧贴内壁的点 G 处有一块面包屑,G 在水面线EF 上,且EG=60cm,一只蚂蚁想从鱼缸外的点 A 沿鱼缸壁爬进鱼缸内的G处吃面包屑.
(1)该蚂蚁应该沿怎样的路线爬行才能使路程最短呢 请你画出它爬行的路线,并用箭头标注.
(2)求蚂蚁爬行的最短路线长.
11.传统文化《周髀算经》 (2024·西安莲湖区模拟)如图所示的图案是我国汉代数学家赵爽在注解《周髀算经》中“赵爽弦图”经修饰后的图形,四边形 ABCD 与四边形EFGH 均为正方形,H是 DE 的中点,阴影部分的面积为27,则AD 的长为 .
12. [问题情境]
勾股定理是一条古老的数学定理,它有很多种证明方法,我国汉代数学家赵爽根据弦图,利用面积法进行证明,著名数学家华罗庚曾提出把“数形关系”(勾股定理)带到其他星球,作为地球人与其他星球“人”进行第一次“谈话”的语言.
[定理表述]
请你根据图(1)中的直角三角形叙述勾股定理;(用文字及符号语言叙述)
[尝试证明]
以图(1)中的直角三角形为基础,可以构造出以a,b为底,以a+b为高的直角梯形(如图(2)),请你利用图(2),验证勾股定理;
[知识拓展]
利用图(2)中的直角梯形,我们可以证明 其证明步骤如下:
∵BC=a+b,AD= ,又在直角梯形 ABCD 中,BC (填大小关系)AD,即 ,
中考提分新题
13.如图(1)是北京国际数学家大会的会标,它取材于我国古代数学家赵爽的“弦图”,是由四个全等的直角三角形拼成.若图(1)中大正方形的面积为24,小正方形的面积为4,现将这四个直角三角形拼成图(2),则图(2)中大正方形的面积为( ).
A. 24 B. 36
C. 40 D. 44
14.数学文化 “毕达哥拉斯树” (2024·大庆中考)如图(1),直角三角形的两个锐角分别是 40°和50°,其三边上分别有一个正方形.执行下面的操作:由两个小正方形向外分别作锐角为40°和50°的直角三角形,再分别以所得到的直角三角形的直角边为边长作正方形.图(2)是1次操作后的图形.图(3)是重复上述步骤若干次后得到的图形,人们把它称为“毕达哥拉斯树”.若图(1)中的直角三角形斜边长为2,则10次操作后图形中所有正方形的面积和为 .
18.1 勾 股 定 理
第1课时 勾 股 定理(1)
1. A [解析]根据勾股定理,得斜边长为 13.故选 A.
2. C [解析]由勾股定理,得
∵以点O为圆心,OB 为半径作弧,与数轴正半轴交于点 P, ∴点 P 表示的实数为 故选C.
3.(1)1 1 2
(2)正方形 M 的面积+正方形 N 的面积=正方形S的面积.
思路引导本题考查正方形面积计算和勾股定理.
(1)由正方形面积公式可知:每个小正方形的面积等于边长的平方,即小正方形M 和小正方形N 的面积都等于1;而正方形S的面积等于4个小方格面积的一半,即等于两个小方格的面积,等于2;(2)由图示可知,BC是直角三角形ABC的斜边,由勾股定理可知
4.96 [解析]由图可得,
∴每个直角三角形的面积为
[解析]如图.由题意,得第一个正方形的边长为2,则
∵△DEC 是等腰直角三角形,
∴第二个正方形的边长为
∵△FGH 是等腰直角三角形,∴第三个正方形的边长为
同理可得,第四个正方形的边长为
∴第n个正方形的边长为
■归纳总结 本题考查图形类规律、等腰直角三角形的性质、勾股定理,掌握勾股定理得到第n个正方形的边长是关键.
6.①②③ [解析]如图,取AB 中点D,连接PD.过点 P作PM⊥AB,以点 B 为圆心,以 BQ 为半径作⊙B,QQ'为⊙B 直径.
∴设AD=DB=a,设DM=b,则MB=a-b.
2
又
①如图,AQ 最小=AB--BQ=10--3=7,AQ'最大 .故①正确;
②如图,PB≤PD+DB,∴PB 最大=PD+DB=4+5=9.故②正确;
③如图,PA≥AD-PD,∴PA 最小=AD-PD=5--4=1.故③正确;
④如图,PQ'≤PD+DB+BQ',∴PQ'最大=PD+ 故④错误.
综上所述,正确的是①②③.
思路引导本题考查了勾股定理,作垂线构造直角三角形是解题的关键.
7.(1)在Rt△ABC中,∠ACB=90°,AC=12,BC=5,由勾股定理,得 ∵AE=22,∴BE=22-13=9,则△ABC 向右平移的距离为9.
(2)由平移的性质可知,CF=BE=9,EF=BC=5,∴四边形AEFC 的周长=AC+AE+EF+CF=12+22+5+9=48.
解后反思 本题考查的是勾股定理、平移的性质,掌握平移的性质和勾股定理是解题的关键.
8.(1)在 Rt△ABD中,AB=5,BD=4,
由勾股定理,得
(2)在Rt△ACD中,
由勾股定理,得 所以△ABC 的周长=AB+BD+CD+AC=
(2)△ABC的面积
(3)△ABC的面积 边上的高,即AB边上的高
关键提醒 本题考查了勾股定理与网格、等积法,掌握勾股定理和利用等积法求AB 边上的高是解题的关键.
10.如图,过点 A 作AD⊥BC,垂足为D.
由等腰三角形的性质知, ∴在 Rt△ADB 中,
①当PA⊥AC时,设BP= xcm,则PD=(4-x) cm,PC=(8-x) cm.
在 Rt△PAD中,
在Rt△PAC 中,
解得x=1.75,即BP=1.75cm.
∴点 P 运动的时间为1.75÷0.25=7(s).
②当PA⊥AB 时,
同理可得PC=1.75cm,
∴BP=8-1.75=6.25(cm).
此时点 P 运动的时间为6.25÷0.25=25(s).
综上所述,当点 P 运动7 s 或25 s时,PA 与腰垂直.
方法总结 本题根据等腰三角形腰的两种情况进行分类讨论,根据勾股定理构建方程,进行运算求解.
11. C [解析]在Rt△ABC中,设AC=x.
∵∠B=30°,∴AB=2x,∠ACB=90°.
由勾股定理,得 解得
在Rt△ACD 中, 设CD=y,则AD=2y,由勾股定理,得 解得y=2(y>0),∴CD=2.
∵AD平分∠CAB,且DC⊥AC,∴点 D 到AB 边的距离等于线段CD 的长,即线段 DE 长度的最小值为2.
■归纳总结 本题考查勾股定理、垂线段最短及含30度角的直角三角形,熟知角平分线的性质及勾股定理是解题的关键.
12.60 [解析]∵AB=AC,∴∠ABC=∠ACB.
∵BF∥AC,∴∠ACB=∠CBF,
∴∠ABC=∠CBF,∴BC平分∠ABF.
如图,过点 C作CM⊥
AB,CN⊥BF,
则CM=CN.
(
CN,且BF=AE,∴S△ACE=S△CBF,
∴四边形EBFC 的面积
∵AC=13,∴AB=13.
设AM=x,则BM=13-x,
由勾股定理,得
解得
∴四边形 EBFC的面积为60.
■ 关键提醒 本题考查了勾股定理、等腰三角形的性质,将四边形EBFC的面积先转化为 再转化为 S△CBA 是解题的关键.
第2课时 勾 股 定 理 (2)
1. B [解析]如图.根据题意,得∠ABC=90°,AB=12m,BC=5m,
故一只小鸟从一棵树的顶端飞到另一棵树的顶端,至少要飞13m.故选 B.
2. B [解析]根据方位角可知两人所走的方向正好构成了直角.根据勾股定理,得他们两人之间的距离为 (米).故选 B.
解后反思 本题考查的是勾股定理的应用,根据题意判断直角三角形是解答本题的关键.
3.2 [解析]∵ ∴AC=BC=2,
4.4 [解析]∵题图中大正方形 ABCD 的面积为34,直角三角形较短的直角边长 AH 为3,
由勾股定理,得 即 (负值舍去),
∴中间小正方形 EFGH 的面积为(
5.由勾股定理,得
(米),
∴到达山顶需要的时间是1344÷120=11.2(分钟).故大约11.2分钟后才能达到山顶.
6. A [解析]· 由勾股定理,得 同理, 故选 A.
7.1.3 [解析]如图,将容器侧面的一半展开,作A 关于EF 的对称点A',∵高为1.2m,底面周长为1m,在容器内壁离容器底部0.3m的点 B 处有一蚊子,此时一只壁虎正好在容器外壁,离容器上沿0.3m与蚊子相对的点A处,∴A'D=0.5m,BD=1.2-0.3+AE=1.2m.在 Rt△A'BD中, 故壁虎捕捉蚊子的最短距离为1.3m.
8.设AB= xm,则BD=(x+5)m.
由AD+DC=AB+BC,得
5+DC=x+20,∴DC=(x+15)m.
在Rt△DBC中,由勾股定理,得 即 解得x=10.
∴BD=x+5=15m.故树高 BD 为15m.
9.(1)由题意可知,∠AOB=90°,AO=24 dm,OB=7 dm,. 故梯子AB的长为25dm.
(2)由题意可知,CD=AB=25dm,AC=4dm,∴OC=AO-AC=24-4=20(dm).
在 Rt△COD 中,由勾股定理,得
∴BD=OD-OB=15-7=8(dm).
故BD 的长为8dm.
10.(1)如图,作点 A 关于BC 的对称点A',连接A'G交BC 于点Q,则蚂蚁沿着A→Q→G的路线爬行时,路程最短.
(2)如图,在 Rt△A'EG 中,A'E=2AB-AE=80cm,EG=60cm,
100 cm.∴蚂蚁爬行的最短路线长为100 cm.
11.3 [解析]由四边形 ABCD 与四边形EFGH 均为正方形,H 是 DE 的中点,可知 E,F,G 分别为AF,BG,CH 的中点,且 AE=EH =DH=HG=CG=FG=BF=EF,
∴EH=AE=3,∴DE=2EH=6.
又
■解后反思 本题考查了直角三角形的性质、勾股定理的证明,找到周围三角形面积和中间正方形面积的关系是解题的关键.
12.[定理表述]
如果直角三角形的两直角边长分别为a,b,斜边长为c,那么
[尝试证明]
∵Rt△ABE≌Rt△ECD,∴∠AEB=∠EDC.
又∠EDC+∠DEC=90°,∴∠AEB+∠DEC=90°,
∴∠AED=90°.
整理,得
[知识拓展]
■方法总结 本题根据全等三角形的性质、面积分割法、勾股定理等知识,证明相关问题.
13. D [解析]如图,直角三角形的两直角边为a,b,斜边为c,
∵图(1)中大正方形的面积是24,
∵小正方形的面积是4,. 2ab=4,∴ab=10,
∴图(2)中最大的正方形的面积为 24+2×10=44.
14.48 [解析]根据勾股定理易得,题图(1)中所有正方形的面积和为8,那么经过1次操作后增加的4个小正方形的面积的和为4,那么经过1次操作后所有正方形的面积和为8+4,同理可得经过2次操作后增加的8个小正方形的面积的和也为4,那么经过2次操作后所有正方形的面积和为8+2×4,那么可推断10次操作后所有正方形的面积和为8+10×4=8+40=48.
难难度突破 本题考查勾股定理的相关知识.根据勾股定理得到以直角三角形各边长为边长的正方形的面积之间的关系是解决本题的关键;难点是得到n次操作后,所有正方形的面积的和等于8+4n.
