勾股定理
图片预览





文档简介
课件24张PPT。勾股定理 — 3(勾股定理的复习) 赵爽弦图化简得: c2 =a2+ b2.勾股定理的证明直角三角形两直角边的平方和等于斜边的平方如果在Rt△ ABC中,∠C=90°,
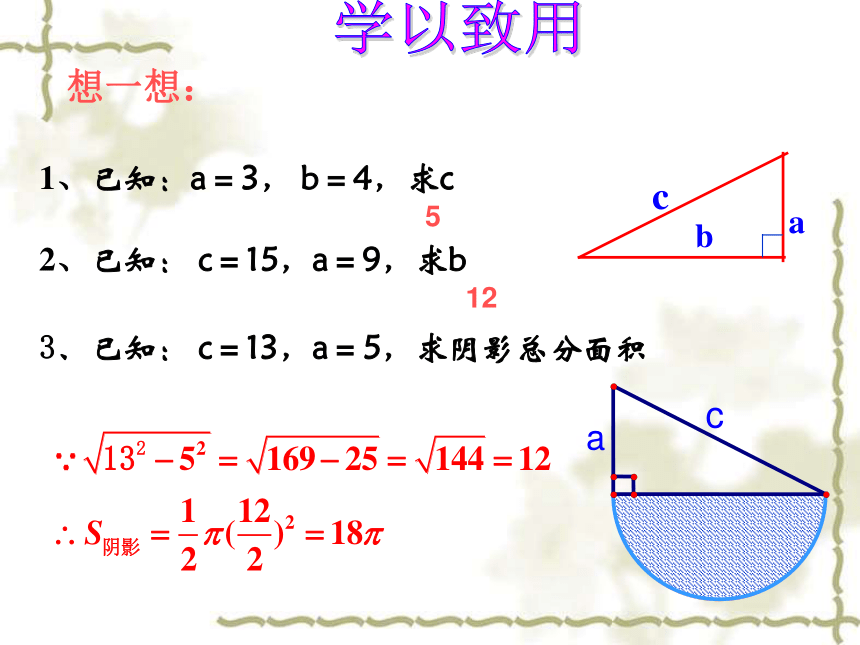
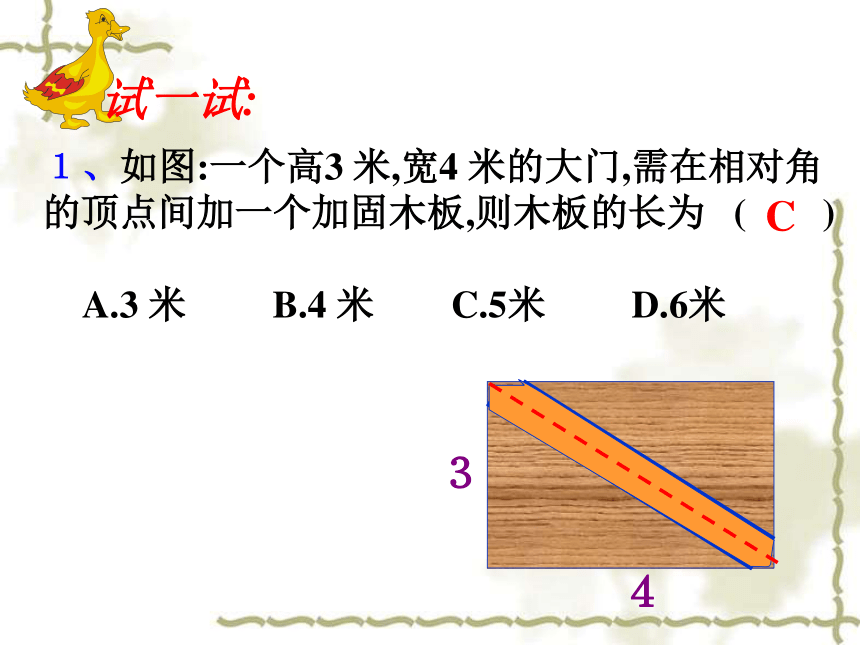
那么勾股定理1、已知:a=3, b=4,求c2、已知: c=15,a=9,求b3、已知: c=13,a=5,求阴影总分面积想一想:学以致用5121、如图:一个高3 米,宽4 米的大门,需在相对角的顶点间加一个加固木板,则木板的长为 ( )A.3 米 B.4 米 C.5米 D.6米C试一试:
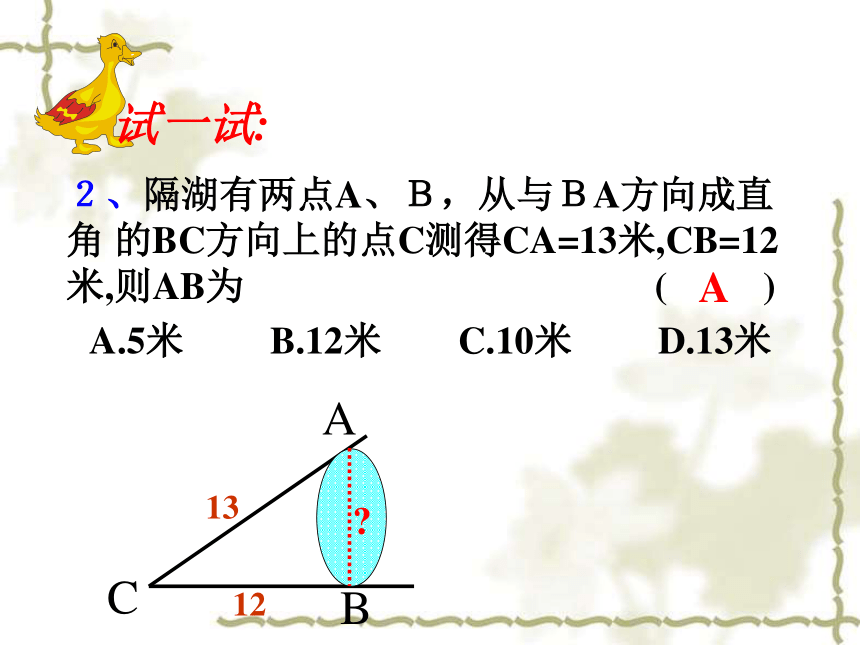
342、隔湖有两点A、B,从与BA方向成直角 的BC方向上的点C测得CA=13米,CB=12米,则AB为 ( )A.5米 B.12米 C.10米 D.13米1312?A试一试:
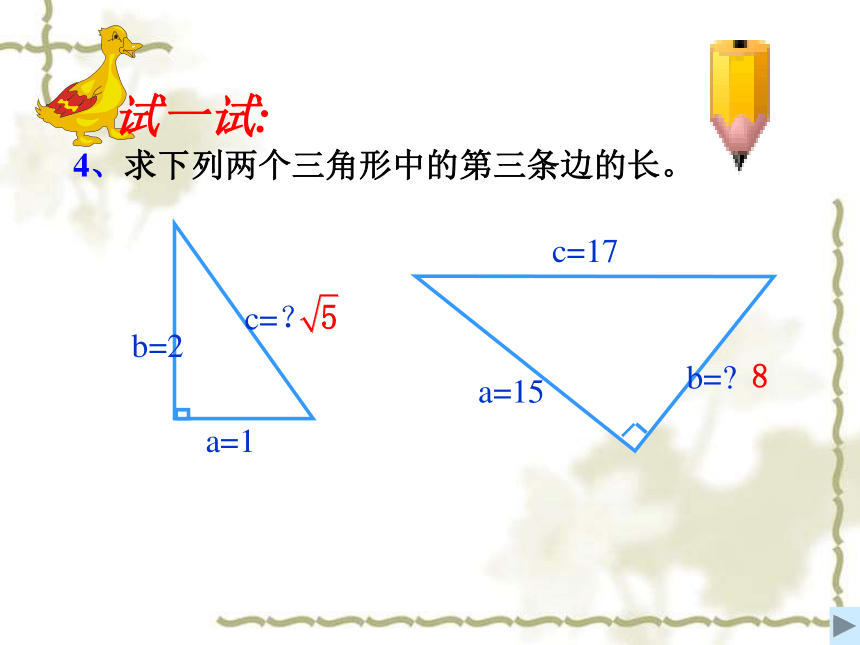
3、一个直角三角形的三边长为三个连续偶数,则它的三边长分别为 ( )A 2、4、6C 4、6、8B试一试:B 6、8、10D 8、10、124、求下列两个三角形中的第三条边的长。试一试:典型例题讲解581630题型四 实践应用题xy10C题型五 拓展创新题2、 如图18-1-19,半圆的直径AB=________.练 一 练1、3、 如图18-1-26是由边长为1m的正方形地转铺设的地面示意图,小明沿图中所示的折线A—B—C所总的路程为________m。(结果保留根号)4、D5、 错解的原因是构成直角三角形斜边没有确定,这就需要分情况讨论。若以50厘米为斜边,40厘米为直角边,则由勾股定理得所需木棒的长度应为30厘米;若以40厘米和50厘米为直角边,则由勾股定理得所需木棒的长度为厘米,所以,以上答案都不对。6、DD考 一 考1、 在我国古代数学著作《九章算术》中记载了一道有趣的问题,这个问题的意思是:有一个水池,水面宽10尺,在水池的中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面,请问这个水池的深度和这根芦苇的长度各是多少?ADBCx15x+1ADA 2、 蚂蚁沿图中的折线从A点爬到D点,一共爬了多少厘米?(小方格的边长为1厘米)GFE作业:课本P70 5题
P71 9、12题
名 题 鉴 赏(趣味数学题)引葭赴岸?? 《九章算术》勾股章第6题:“今有池方一丈,葭生其中央.出水一尺,引葭赴岸,适与岸齐.问水深、葭长各几何.” 意思是:有一水池一丈见方,池中生有一棵类似芦苇的植物,露出水面一尺,如把它引向岸边,正好与岸边齐,问水有多深,该植物有多长? 这一问题在世界数学史上很有影响.印度古代数学家婆什迦罗的《丽罗瓦提》一书中有按这一问题改编的“风动红莲”;阿拉伯数学家阿尔?卡西的《算术之钥》也有类似的“池中长茅”问题;欧洲《十六世纪的算术》一书中又有“圆池芦苇”问题.所有问题内容大体一致,但比我国此类问题的研究要晚几百年甚至上千年!??? 风动红莲?? 波平如镜一湖面,
半尺高处出红莲;
鲜艳多姿湖中立,
猛遭狂风吹一边。
红莲斜卧水淹面,
距根生处两尺远;
渔翁发现忙思考,
湖水深浅有多少? 2x笨人执竿要进屋,无奈门框拦住竹,
横多四尺竖多二,没法急得放声哭.
有个邻居聪明者,教他斜竿对两角,
笨伯依言试一试,不多不少刚抵足.
借问竿长多少数,谁人算出我佩服.执竿进屋设杆长为x尺x-4X-2x
那么勾股定理1、已知:a=3, b=4,求c2、已知: c=15,a=9,求b3、已知: c=13,a=5,求阴影总分面积想一想:学以致用5121、如图:一个高3 米,宽4 米的大门,需在相对角的顶点间加一个加固木板,则木板的长为 ( )A.3 米 B.4 米 C.5米 D.6米C试一试:
342、隔湖有两点A、B,从与BA方向成直角 的BC方向上的点C测得CA=13米,CB=12米,则AB为 ( )A.5米 B.12米 C.10米 D.13米1312?A试一试:
3、一个直角三角形的三边长为三个连续偶数,则它的三边长分别为 ( )A 2、4、6C 4、6、8B试一试:B 6、8、10D 8、10、124、求下列两个三角形中的第三条边的长。试一试:典型例题讲解581630题型四 实践应用题xy10C题型五 拓展创新题2、 如图18-1-19,半圆的直径AB=________.练 一 练1、3、 如图18-1-26是由边长为1m的正方形地转铺设的地面示意图,小明沿图中所示的折线A—B—C所总的路程为________m。(结果保留根号)4、D5、 错解的原因是构成直角三角形斜边没有确定,这就需要分情况讨论。若以50厘米为斜边,40厘米为直角边,则由勾股定理得所需木棒的长度应为30厘米;若以40厘米和50厘米为直角边,则由勾股定理得所需木棒的长度为厘米,所以,以上答案都不对。6、DD考 一 考1、 在我国古代数学著作《九章算术》中记载了一道有趣的问题,这个问题的意思是:有一个水池,水面宽10尺,在水池的中央有一根新生的芦苇,它高出水面1尺,如果把这根芦苇垂直拉向岸边,它的顶端恰好到达岸边的水面,请问这个水池的深度和这根芦苇的长度各是多少?ADBCx15x+1ADA 2、 蚂蚁沿图中的折线从A点爬到D点,一共爬了多少厘米?(小方格的边长为1厘米)GFE作业:课本P70 5题
P71 9、12题
名 题 鉴 赏(趣味数学题)引葭赴岸?? 《九章算术》勾股章第6题:“今有池方一丈,葭生其中央.出水一尺,引葭赴岸,适与岸齐.问水深、葭长各几何.” 意思是:有一水池一丈见方,池中生有一棵类似芦苇的植物,露出水面一尺,如把它引向岸边,正好与岸边齐,问水有多深,该植物有多长? 这一问题在世界数学史上很有影响.印度古代数学家婆什迦罗的《丽罗瓦提》一书中有按这一问题改编的“风动红莲”;阿拉伯数学家阿尔?卡西的《算术之钥》也有类似的“池中长茅”问题;欧洲《十六世纪的算术》一书中又有“圆池芦苇”问题.所有问题内容大体一致,但比我国此类问题的研究要晚几百年甚至上千年!??? 风动红莲?? 波平如镜一湖面,
半尺高处出红莲;
鲜艳多姿湖中立,
猛遭狂风吹一边。
红莲斜卧水淹面,
距根生处两尺远;
渔翁发现忙思考,
湖水深浅有多少? 2x笨人执竿要进屋,无奈门框拦住竹,
横多四尺竖多二,没法急得放声哭.
有个邻居聪明者,教他斜竿对两角,
笨伯依言试一试,不多不少刚抵足.
借问竿长多少数,谁人算出我佩服.执竿进屋设杆长为x尺x-4X-2x
