九年级数学上册人教版 24.2.2节《直线和圆的位置关系》课时复习题(含答案)
文档属性
| 名称 | 九年级数学上册人教版 24.2.2节《直线和圆的位置关系》课时复习题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-15 15:33:23 | ||
图片预览




文档简介
九年级数学上册人教版第二十四章第2.2节《直线和圆的位置关系》课时复习题
一、单选题
1.已知的半径是5,直线与相交,则圆心到直线的距离可能是( )
A.4 B.5 C.6 D.7
2.如图,是⊙的切线,切点为A,的延长线交⊙于点B,连接.若,则的度数为( )
A. B. C. D.
3.如图,是△ABC的外接圆,为的切线,经过圆心,且,则的度数为 .
A. B. C. D.
4.如图,已知点在上,,直线与相切,切点为,且为的中点,则等于( )
A. B. C. D.
5.如图,有一块三角形铁皮余料,,,.若从中剪一个面积最大的半圆,则半圆的圆心在( )
A.边上 B.边上 C.边上 D.内
6.如图,的切线交直径的延长线于点为切点.若的半径为2,则的长为( )
A. B.2 C. D.2
7.如图,点是外一定点,连接线段,与交于点.按照如下尺规作图的步骤进行操作:①分别以,为圆心,以大于长为半径画弧,两弧交于点,,作直线,交于点;②以点为圆心,以为半径作,与交于点,两点;③连接,,,,,线段与相交于点.则下列说法中不一定正确的是( )
A.,均为与的切线 B.
C. D.
8.如图,正五边形的内切圆分别切,于点,.若为优弧上的一点,连接,,则等于( )
A. B. C. D.
9.如图,在中,,是△ABC的内切圆,若,,则图中的面积为( )
A.5.5 B.2.75 C.6.05 D.3.025
10.如图,是外一点,交于点,.甲、乙两人想作一条通过点与相切的直线,其作法如下:
甲:以点为圆心,长为半径画弧,交于点,则直线即为所求.
乙:过点作直线,以点为圆心,长为半径画弧,交射线于点,连接,交于点,则直线即为所求.
对于甲、乙两人的作法,下列判断正确的是( )
A.甲正确,乙错误 B.乙正确,甲错误
C.两人都正确 D.两人都错误
二、填空题
11.如图,,是圆的切线,切点分别为,,连接,.如果,那么的度数为 .
12.如图,把置于平面直角坐标系中,点的坐标为,点的坐标为,点是内切圆的圆心.将沿轴的正方向作无滑动滚动,使它的三边依次与轴重合,第一次滚动后圆心为,第二次滚动后圆心为,依此规律,第2025次滚动后,内切圆的圆心的坐标是 .
13.如图,是半圆O的直径,C为延长线上一点,切半圆O于点D,连结,.若,则等于 度.
14.如图,在矩形中,点E在边上,连接,平分,点O是的内心,连接,,若,则的长为 .
15.如图,在等腰三角形中,,经过A,B两点的与边切于点A,与边交于点D,为的直径,连结,若,则的度数为 .
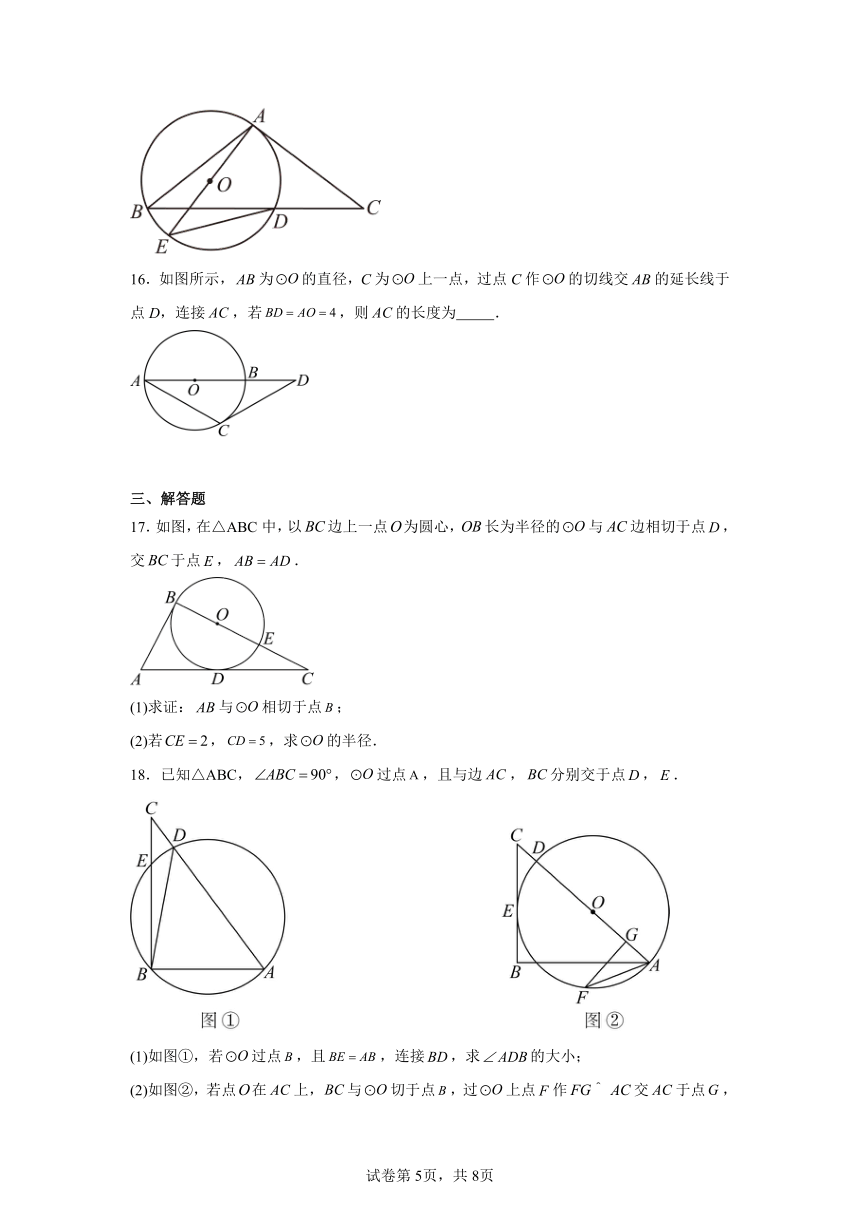
16.如图所示,为的直径,C为上一点,过点C作的切线交的延长线于点D,连接,若,则的长度为 .
三、解答题
17.如图,在△ABC中,以边上一点为圆心,长为半径的与边相切于点,交于点,.
(1)求证:与相切于点;
(2)若,,求的半径.
18.已知△ABC,,过点,且与边,分别交于点,.
(1)如图①,若过点,且,连接,求的大小;
(2)如图②,若点在上,与切于点,过上点作交于点,连接,若,,求的长.
19.如图,△ABC内接于,是的直径,是的平分线,交于点D,过点D作的切线交的延长线于点E.试判断与的位置关系,并说明理由.
20.如图,与相切于点B,交于点F,延长交于点C,连接,点D为上一点, 且F为弧 的中点, 连接.
(1)求证: 是的切线;
(2)若,,求的半径的长.
21.是△ABC的外接圆,是的直径,点为上一点,过点作与的延长线交于点,连接与交于点.
(1)如图①,若,求和大小;
(2)如图②,若恰好切于点,且,求的半径和的长.
22.综合与实践
活动主题 扇面制作
活动情景 如图1,扇面字画是一种传统的中国艺术形式,它将字和绘画结合在扇面上,形成一种独特的艺术风格.为了迎接我市2025年传统民俗文化活动的到来,某班组织同学们开展扇面制作展示活动.如图2所示,扇面形状为扇环,已知,,.
活动小组 甲组 乙组
制作工具 直尺、三角板、量角器、圆规、剪刀
制作材料
【任务一】确定弦的长度.
如图2,请你求出 所对弦的长度.
【任务二】设计甲组扇面.
如图3,已知甲组的圆形卡纸直径为请运用表格中所给工具在中设计与图2相同的扇面,并标出相应数据.
【任务三】确定卡纸大小.
如图4,乙组利用矩形卡纸,恰好设计出与图2相同的扇面,求矩形卡纸的最小规格(即矩形的边长).
23.问题背景:如图(1)在四边形中,,,探究线段、、之间的数量关系.小明探究此问题的思路是:将绕点逆时针旋转到处,点B、C分别落在点A、E处(如图(2)),易证点C、A、E在同一条直线上,并且是等腰直角三角形,所以,从而得出结论:.
简单应用:
(1)在图(1)中,若,,求的长;
(2)如图(3)是⊙O的直径,点C、D在⊙O上,,若,,求的长.
24.已知⊙O是ABC的外接圆,BC为⊙O的直径,弧AB上一点D满足DB=DA,连结CD交AB于点E.
(1)求∠AED+∠ABC的值.
(2)求证:AC BC=CE CD;
(3)连接OE,若∠BOE=∠BEO,求BEO与BED的面积比.
试卷第1页,共3页
试卷第1页,共3页
《九年级数学上册人教版第二十四章第2.2节《直线和圆的位置关系》课时复习题》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A A B A A B C B D C
11.
12.
13.130
14./6.25
15.
16.
17.(1)证明:如下图所示,连接,,
在与中,
,
,
,
与相切于,
,
,
是的半径,
与相切于;
(2)解:在中,,
,
,,
,
解得.
18.(1)解:连接,
过点,,
为直径,
,
,
.
(2)解:连接,,设半径为,
与切于点,
.
,
,是等腰直角三角形,
,
,
.
,
,
在中,,
在中,.
19.解:,理由如下:
连接,交于点G,
∵是的切线,
∴,
∵是的平分线,
∴,
由圆周角定理可知:,
∴,
∴,
∴,
∵是的直径,
∴,
∴,
∴.
20.(1)证明:如图所示,连接,
∵与相切于点B,
∴ ,
∵F为的中点,
∴,
又∵,
∴,
∴,
∵是的半径,
∴是的切线;
(2)解:设的半径为r,则,
在中,由勾股定理得,
∴,
解得,
∴的半径为.
21.(1)解:∵是的直径,
∴,
∵,
∴,
∵,
∴,
∴.
(2)解:连接,并延长交于一点H,如图所示:
∵恰好切于点,
∴,
由(1)得,
∴四边形是矩形,
∴,
∴,
∵,
∴,
设的半径为,
则,
∴,
解得,
在中,则
∴.
22.任务一:解:过点O作,交于点,
,,
,
,
,,
,
任务二:如图,是以直径为底边,底角为度,由任务一可知,,取,以O为圆心,分别以、为半径画弧,即可得到扇面.
任务三:分两种情况:
①如图所示:当与矩形两边相切时,过点作,则矩形为最小规格矩形,
∵,,,
∴,,,
∵当与矩形两边相切,
∴最小规格矩形的边长为、;
②如图,当矩形的边与相切于点M,且A、B两点分别在上,C、D在上;连接交于点N,连接;
由题意知,,,
∴,
∴;
由勾股定理得,
∴;
同理:,
∴,
此时最小规格边长分别为;
综上,最小规格矩形边长为、或.
23.解:(1)由题意知:,
∴
∴;
故答案为3;
(2)如图3,连接、、,
∵是⊙O的直径,
∴
∵
∴,
∵,,
∴由勾股定理得:,
由图1得:
∴.
24.(1)解:∵BC是直径,
∴∠CAB=90°,
∴∠ACB+∠ABC=90°,
∴∠ACB+∠ABC=45°,
∵BD=AD,
∴,
∴∠ACD=∠BCD,
∵∠AED=∠ACD+∠CAE,
∴∠AED+∠ABC=90°+∠ACB+∠ABC=135°;
(2)证明:∵
∴∠ACD=∠BCE,
∵∠CBE=∠ADC,
∴△CBE∽△CDA,
∴,
∴AC BC=CE CD;
(3)解:如图,过点B作BT⊥OE交CD于点T,连接OT.
∵BO=BE,
∴BO垂直平分线段OE,TB平分∠ABC,
∴TO=TE,
∴TB平分∠OTE,
∵CE平分∠ACB,
∴∠BTD=∠TCB+∠TBC=(∠ACB+∠ABC)=45°,
∴∠OTE=90°,
∴OT⊥CD,
∴CT=TD,
∵BC是直径,
∴∠BDT=90°,
∴∠BTD=∠DBT=45°,
∴BD=DT=CT,
∵CO=OB,CT=TD,
∴BD=2OT,
∴DT=CT=2ET,
∴CE=3DE,
∴S△BEC=3S△DEB,
∵BO=OC,
∴S△BEC=2S△BEO,
∴2S△BEO=3S△DEB,
∴.
答案第1页,共2页
答案第1页,共2页
一、单选题
1.已知的半径是5,直线与相交,则圆心到直线的距离可能是( )
A.4 B.5 C.6 D.7
2.如图,是⊙的切线,切点为A,的延长线交⊙于点B,连接.若,则的度数为( )
A. B. C. D.
3.如图,是△ABC的外接圆,为的切线,经过圆心,且,则的度数为 .
A. B. C. D.
4.如图,已知点在上,,直线与相切,切点为,且为的中点,则等于( )
A. B. C. D.
5.如图,有一块三角形铁皮余料,,,.若从中剪一个面积最大的半圆,则半圆的圆心在( )
A.边上 B.边上 C.边上 D.内
6.如图,的切线交直径的延长线于点为切点.若的半径为2,则的长为( )
A. B.2 C. D.2
7.如图,点是外一定点,连接线段,与交于点.按照如下尺规作图的步骤进行操作:①分别以,为圆心,以大于长为半径画弧,两弧交于点,,作直线,交于点;②以点为圆心,以为半径作,与交于点,两点;③连接,,,,,线段与相交于点.则下列说法中不一定正确的是( )
A.,均为与的切线 B.
C. D.
8.如图,正五边形的内切圆分别切,于点,.若为优弧上的一点,连接,,则等于( )
A. B. C. D.
9.如图,在中,,是△ABC的内切圆,若,,则图中的面积为( )
A.5.5 B.2.75 C.6.05 D.3.025
10.如图,是外一点,交于点,.甲、乙两人想作一条通过点与相切的直线,其作法如下:
甲:以点为圆心,长为半径画弧,交于点,则直线即为所求.
乙:过点作直线,以点为圆心,长为半径画弧,交射线于点,连接,交于点,则直线即为所求.
对于甲、乙两人的作法,下列判断正确的是( )
A.甲正确,乙错误 B.乙正确,甲错误
C.两人都正确 D.两人都错误
二、填空题
11.如图,,是圆的切线,切点分别为,,连接,.如果,那么的度数为 .
12.如图,把置于平面直角坐标系中,点的坐标为,点的坐标为,点是内切圆的圆心.将沿轴的正方向作无滑动滚动,使它的三边依次与轴重合,第一次滚动后圆心为,第二次滚动后圆心为,依此规律,第2025次滚动后,内切圆的圆心的坐标是 .
13.如图,是半圆O的直径,C为延长线上一点,切半圆O于点D,连结,.若,则等于 度.
14.如图,在矩形中,点E在边上,连接,平分,点O是的内心,连接,,若,则的长为 .
15.如图,在等腰三角形中,,经过A,B两点的与边切于点A,与边交于点D,为的直径,连结,若,则的度数为 .
16.如图所示,为的直径,C为上一点,过点C作的切线交的延长线于点D,连接,若,则的长度为 .
三、解答题
17.如图,在△ABC中,以边上一点为圆心,长为半径的与边相切于点,交于点,.
(1)求证:与相切于点;
(2)若,,求的半径.
18.已知△ABC,,过点,且与边,分别交于点,.
(1)如图①,若过点,且,连接,求的大小;
(2)如图②,若点在上,与切于点,过上点作交于点,连接,若,,求的长.
19.如图,△ABC内接于,是的直径,是的平分线,交于点D,过点D作的切线交的延长线于点E.试判断与的位置关系,并说明理由.
20.如图,与相切于点B,交于点F,延长交于点C,连接,点D为上一点, 且F为弧 的中点, 连接.
(1)求证: 是的切线;
(2)若,,求的半径的长.
21.是△ABC的外接圆,是的直径,点为上一点,过点作与的延长线交于点,连接与交于点.
(1)如图①,若,求和大小;
(2)如图②,若恰好切于点,且,求的半径和的长.
22.综合与实践
活动主题 扇面制作
活动情景 如图1,扇面字画是一种传统的中国艺术形式,它将字和绘画结合在扇面上,形成一种独特的艺术风格.为了迎接我市2025年传统民俗文化活动的到来,某班组织同学们开展扇面制作展示活动.如图2所示,扇面形状为扇环,已知,,.
活动小组 甲组 乙组
制作工具 直尺、三角板、量角器、圆规、剪刀
制作材料
【任务一】确定弦的长度.
如图2,请你求出 所对弦的长度.
【任务二】设计甲组扇面.
如图3,已知甲组的圆形卡纸直径为请运用表格中所给工具在中设计与图2相同的扇面,并标出相应数据.
【任务三】确定卡纸大小.
如图4,乙组利用矩形卡纸,恰好设计出与图2相同的扇面,求矩形卡纸的最小规格(即矩形的边长).
23.问题背景:如图(1)在四边形中,,,探究线段、、之间的数量关系.小明探究此问题的思路是:将绕点逆时针旋转到处,点B、C分别落在点A、E处(如图(2)),易证点C、A、E在同一条直线上,并且是等腰直角三角形,所以,从而得出结论:.
简单应用:
(1)在图(1)中,若,,求的长;
(2)如图(3)是⊙O的直径,点C、D在⊙O上,,若,,求的长.
24.已知⊙O是ABC的外接圆,BC为⊙O的直径,弧AB上一点D满足DB=DA,连结CD交AB于点E.
(1)求∠AED+∠ABC的值.
(2)求证:AC BC=CE CD;
(3)连接OE,若∠BOE=∠BEO,求BEO与BED的面积比.
试卷第1页,共3页
试卷第1页,共3页
《九年级数学上册人教版第二十四章第2.2节《直线和圆的位置关系》课时复习题》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 A A B A A B C B D C
11.
12.
13.130
14./6.25
15.
16.
17.(1)证明:如下图所示,连接,,
在与中,
,
,
,
与相切于,
,
,
是的半径,
与相切于;
(2)解:在中,,
,
,,
,
解得.
18.(1)解:连接,
过点,,
为直径,
,
,
.
(2)解:连接,,设半径为,
与切于点,
.
,
,是等腰直角三角形,
,
,
.
,
,
在中,,
在中,.
19.解:,理由如下:
连接,交于点G,
∵是的切线,
∴,
∵是的平分线,
∴,
由圆周角定理可知:,
∴,
∴,
∴,
∵是的直径,
∴,
∴,
∴.
20.(1)证明:如图所示,连接,
∵与相切于点B,
∴ ,
∵F为的中点,
∴,
又∵,
∴,
∴,
∵是的半径,
∴是的切线;
(2)解:设的半径为r,则,
在中,由勾股定理得,
∴,
解得,
∴的半径为.
21.(1)解:∵是的直径,
∴,
∵,
∴,
∵,
∴,
∴.
(2)解:连接,并延长交于一点H,如图所示:
∵恰好切于点,
∴,
由(1)得,
∴四边形是矩形,
∴,
∴,
∵,
∴,
设的半径为,
则,
∴,
解得,
在中,则
∴.
22.任务一:解:过点O作,交于点,
,,
,
,
,,
,
任务二:如图,是以直径为底边,底角为度,由任务一可知,,取,以O为圆心,分别以、为半径画弧,即可得到扇面.
任务三:分两种情况:
①如图所示:当与矩形两边相切时,过点作,则矩形为最小规格矩形,
∵,,,
∴,,,
∵当与矩形两边相切,
∴最小规格矩形的边长为、;
②如图,当矩形的边与相切于点M,且A、B两点分别在上,C、D在上;连接交于点N,连接;
由题意知,,,
∴,
∴;
由勾股定理得,
∴;
同理:,
∴,
此时最小规格边长分别为;
综上,最小规格矩形边长为、或.
23.解:(1)由题意知:,
∴
∴;
故答案为3;
(2)如图3,连接、、,
∵是⊙O的直径,
∴
∵
∴,
∵,,
∴由勾股定理得:,
由图1得:
∴.
24.(1)解:∵BC是直径,
∴∠CAB=90°,
∴∠ACB+∠ABC=90°,
∴∠ACB+∠ABC=45°,
∵BD=AD,
∴,
∴∠ACD=∠BCD,
∵∠AED=∠ACD+∠CAE,
∴∠AED+∠ABC=90°+∠ACB+∠ABC=135°;
(2)证明:∵
∴∠ACD=∠BCE,
∵∠CBE=∠ADC,
∴△CBE∽△CDA,
∴,
∴AC BC=CE CD;
(3)解:如图,过点B作BT⊥OE交CD于点T,连接OT.
∵BO=BE,
∴BO垂直平分线段OE,TB平分∠ABC,
∴TO=TE,
∴TB平分∠OTE,
∵CE平分∠ACB,
∴∠BTD=∠TCB+∠TBC=(∠ACB+∠ABC)=45°,
∴∠OTE=90°,
∴OT⊥CD,
∴CT=TD,
∵BC是直径,
∴∠BDT=90°,
∴∠BTD=∠DBT=45°,
∴BD=DT=CT,
∵CO=OB,CT=TD,
∴BD=2OT,
∴DT=CT=2ET,
∴CE=3DE,
∴S△BEC=3S△DEB,
∵BO=OC,
∴S△BEC=2S△BEO,
∴2S△BEO=3S△DEB,
∴.
答案第1页,共2页
答案第1页,共2页
同课章节目录
