5.3三角函数诱导公式 教学设计(表格式)
文档属性
| 名称 | 5.3三角函数诱导公式 教学设计(表格式) |  | |
| 格式 | docx | ||
| 文件大小 | 97.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-15 16:22:22 | ||
图片预览


文档简介
教学设计
课题 三角函数诱导公式
课型 新授课 章/单元复习课□ 专题复习课□ 习题/试卷讲评课□ 学科实践活动课□ 其他□
教学内容分析
教材首先通过探究角的终边的对称性,引导学生利用三角函数的定义得到公式二、三、四,再用具体的例子,巩固公式。整个过程发展了学生直观想象、数学抽象的数学学科核心素养;通过公式的应用,又提升了学生数学运算的数学学科核心素养.
学习者分析
经过前面的学习,学生已经具有一定的逻辑推理能力;学生已经掌握了三角函数的定义、诱导公式一及关于原点(x轴、y轴)对称的点的坐标特点,高一学生表现欲强,希望得到关注,希望被肯定。
学习目标确定
1.能借助单位圆的对称性,利用三角函数的定义推导出诱导公式二、三、四,培养直观现象、逻辑推理、数学抽象的核心素养; 2.能正确运用诱导公式将任意角的三角函数化为锐角的三角函数,提升数学运算的核心素养; 3.能解决有关三角函数求值、化简和恒等式证明问题,强化逻辑推理、数学运算的核心素养。
学习重点难点
重点:能借助单位圆的对称性,利用三角函数的定义推导出诱导公式二、三、四,能正确运用诱导公式将任意角的三角函数化为锐角的三角函数; 难点:发现圆的对称性与三角函数之间的关系,建立联系。
学习条件支持
小组式讨论桌椅摆放模式、黑板、希沃白板、展示白板,以及电子展台等。
学习活动设计
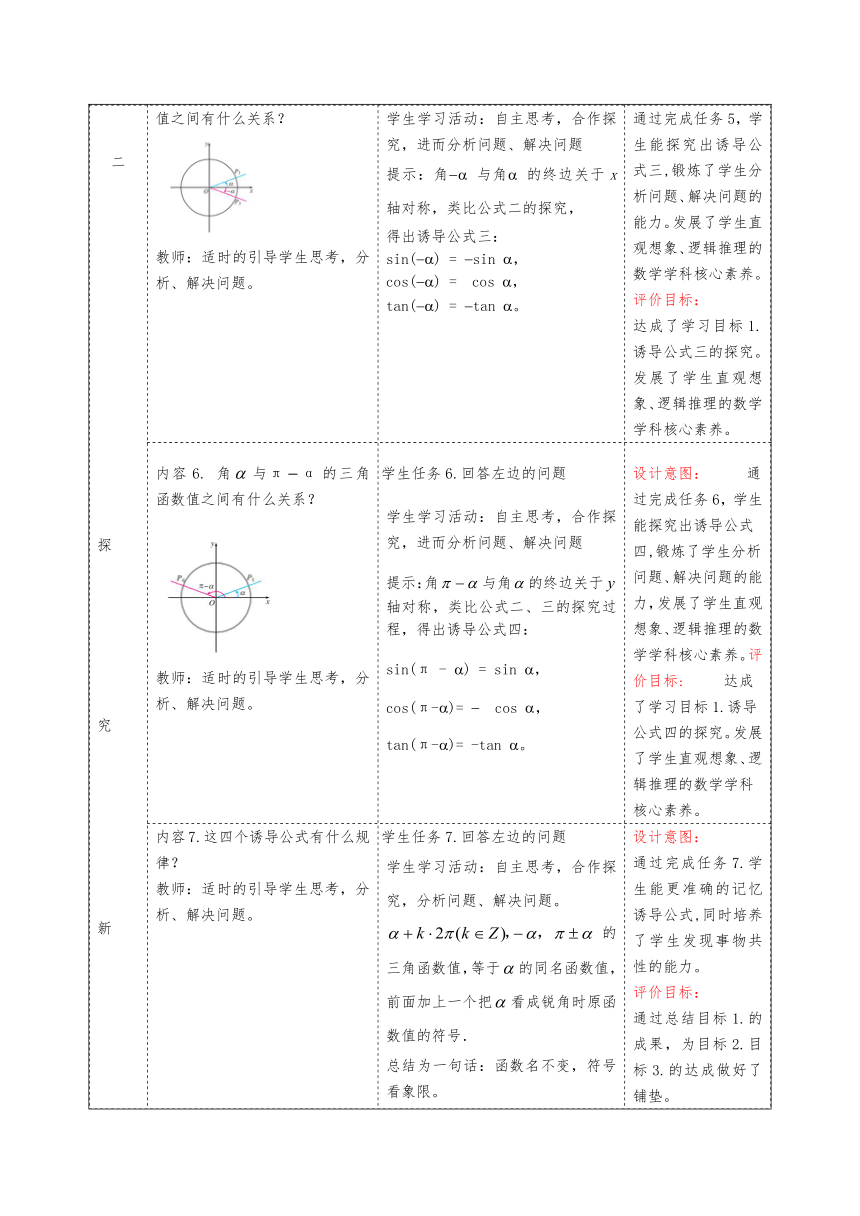
过程学习内容与教师活动(引领性问题)学生任务或学习活动设计设计意图或评价目标 环 节 一 复 习 旧 知内容1. (创设情境) 三角函数的定义是什么? 教师活动:引导学生回忆定义。 学生任务1.回答左边的问题 学生学习活动:自主解决问题设计意图: 通过回忆三角函数的定义,学生能应用定义求三角函数值。 评价目标: 为目标1.的达成做好铺垫。提升学生的逻辑推理的核心素养。内容2. (创设情境)终边相同的角的同一三角函数值有什么关系 教师活动:引导学生回忆诱导公式一学生任务2.回答左边的问题 学生学习活动:自主解决问题设计意图: 通过回忆三角函数的诱导公式一,能理解公式一的推导过程,并能应用公式一求解三角函数值。 评价目标: 为目标1.的达成做好铺垫。提升学生的数学运算的核心素养。内容3. (创设情境) 角与α的终边 有何位置关系 角 -α与α的终边 有何位置关系 角与α的终边 有何位置关系 已知任意角α的终边与单位圆相交于点P(x, y),请同学们思考回答点P关于原点、x轴、y轴对称的三个点的坐标是什么 教师:适时的引导学生思考。学生任务3.回答左边的问题 学生学习活动:自主思考,合作探究,进而解决问题设计意图: 通过完成任务3,学生会发现角的终边的对称关系,并会求关于原点、x轴及y轴对称的点的坐标。 评价目标: 为目标1.的达成奠定思维基础。提升学生的逻辑推理的核心素养。 环 节 二 探 究 新 知 内容4. 如图, 角的三角函数值与的三角函数值之间有什么关系? 教师:适时的引导学生思考,分析、解决问题。学生任务4.回答左边的问题 学生学习活动:自主思考,合作探究,进而分析问题、解决问题 提示:角π + 与角 的终边关于原点O对称, , 得出诱导公式二: sin(π + ) = sin , cos(π + ) = cos , tan(π + ) = tan 。设计意图: 通过完成任务4,学生能探究出诱导公式二,锻炼了学生分析问题、解决问题的能力。 评价目标: 达成了学习目标1.诱导公式二的探究。发展了学生直观想象、逻辑推理的数学学科核心素养。内容5. 角与的三角函数值之间有什么关系? 教师:适时的引导学生思考,分析、解决问题。学生任务5.回答左边的问题 学生学习活动:自主思考,合作探究,进而分析问题、解决问题 提示:角 与角 的终边关于x轴对称,类比公式二的探究, 得出诱导公式三: sin() = sin , cos() = cos , tan() = tan 。设计意图: 通过完成任务5,学生能探究出诱导公式三,锻炼了学生分析问题、解决问题的能力。发展了学生直观想象、逻辑推理的数学学科核心素养。 评价目标: 达成了学习目标1.诱导公式三的探究。发展了学生直观想象、逻辑推理的数学学科核心素养。内容6. 角与的三角函数值之间有什么关系? 教师:适时的引导学生思考,分析、解决问题。学生任务6.回答左边的问题 学生学习活动:自主思考,合作探究,进而分析问题、解决问题 提示:角与角的终边关于轴对称,类比公式二、三的探究过程,得出诱导公式四: sin(π - ) = sin , cos(π-)= cos , tan(π-)= -tan 。设计意图: 通过完成任务6,学生能探究出诱导公式四,锻炼了学生分析问题、解决问题的能力,发展了学生直观想象、逻辑推理的数学学科核心素养。评价目标: 达成了学习目标1.诱导公式四的探究。发展了学生直观想象、逻辑推理的数学学科核心素养。内容7.这四个诱导公式有什么规律? 教师:适时的引导学生思考,分析、解决问题。学生任务7.回答左边的问题 学生学习活动:自主思考,合作探究,分析问题、解决问题。 的三角函数值,等于的同名函数值,前面加上一个把看成锐角时原函数值的符号. 总结为一句话:函数名不变,符号看象限。设计意图: 通过完成任务7.学生能更准确的记忆诱导公式,同时培养了学生发现事物共性的能力。 评价目标: 通过总结目标1.的成果,为目标2.目标3.的达成做好了铺垫。内容8. 任意角的三角函数化为锐角三角函数的步骤? 教师:适时的引导学生思考,分析、解决问题。学生任务8.回答左边的问题 学生学习活动:自主思考,合作探究,分析问题、解决问题。 利用公式一~四把任意角的三角函数转化为锐角的三角函数,一般可按下列步骤进行: 上述步骤体现了由未知转化为已知的转化与化归的思想方法.设计意图: 通过完成任务8,学生会把任意角的三角函数化为锐角三角函数,培养了学生分析问题、解决问题的能力。 评价目标: 通过完成任务8,达成了学习目标2.的思维基础。发展了学生逻辑推理的核心素养。 环 节 三 例 题 分 析内容9.例题分析 例1 利用公式求下列三角函数值: 例2 化简 学生任务9.回答左边的问题 学生学习活动:自主思考,合作探究,分析问题、解决问题。 解: 解: , 所以 原式设计意图: 通过任务9的完成,学生能将任意角的三角函数化为锐角三角函数,能应用诱导公式一~四进行三角式的化简、求值。 评价目标: 通过完成任务9, 达成了学习目标2.学习目标3。发展了逻辑推理、数学运算的数学学科核心素养。 课 堂 检 测化简: 2.填表:
设计意图: 通过课堂检测,学生能进一步巩固诱导公式的综合应用,并检测自己完成的情况,提高了发现问题、提出问题、分析问题、解决问题的能力,评价目标: 通过课堂检测,更加确保了目标1.~目标3.的达成。发展了逻辑推理、数学运算学科核心素养。 课 堂 小 结 设计意图: 通过总结,学生进一步巩固了诱导公式及其应用,提高了自身的概括能力。 评价目标: 通过总结,学生再次明确了目标1.~目标3.的达成。
板书设计
三 三角函数的诱导公式第1课时 诱 诱导公式一 诱 诱导公式二 诱导公式三 诱导公式四例题分析 课堂小结
课题 三角函数诱导公式
课型 新授课 章/单元复习课□ 专题复习课□ 习题/试卷讲评课□ 学科实践活动课□ 其他□
教学内容分析
教材首先通过探究角的终边的对称性,引导学生利用三角函数的定义得到公式二、三、四,再用具体的例子,巩固公式。整个过程发展了学生直观想象、数学抽象的数学学科核心素养;通过公式的应用,又提升了学生数学运算的数学学科核心素养.
学习者分析
经过前面的学习,学生已经具有一定的逻辑推理能力;学生已经掌握了三角函数的定义、诱导公式一及关于原点(x轴、y轴)对称的点的坐标特点,高一学生表现欲强,希望得到关注,希望被肯定。
学习目标确定
1.能借助单位圆的对称性,利用三角函数的定义推导出诱导公式二、三、四,培养直观现象、逻辑推理、数学抽象的核心素养; 2.能正确运用诱导公式将任意角的三角函数化为锐角的三角函数,提升数学运算的核心素养; 3.能解决有关三角函数求值、化简和恒等式证明问题,强化逻辑推理、数学运算的核心素养。
学习重点难点
重点:能借助单位圆的对称性,利用三角函数的定义推导出诱导公式二、三、四,能正确运用诱导公式将任意角的三角函数化为锐角的三角函数; 难点:发现圆的对称性与三角函数之间的关系,建立联系。
学习条件支持
小组式讨论桌椅摆放模式、黑板、希沃白板、展示白板,以及电子展台等。
学习活动设计
过程学习内容与教师活动(引领性问题)学生任务或学习活动设计设计意图或评价目标 环 节 一 复 习 旧 知内容1. (创设情境) 三角函数的定义是什么? 教师活动:引导学生回忆定义。 学生任务1.回答左边的问题 学生学习活动:自主解决问题设计意图: 通过回忆三角函数的定义,学生能应用定义求三角函数值。 评价目标: 为目标1.的达成做好铺垫。提升学生的逻辑推理的核心素养。内容2. (创设情境)终边相同的角的同一三角函数值有什么关系 教师活动:引导学生回忆诱导公式一学生任务2.回答左边的问题 学生学习活动:自主解决问题设计意图: 通过回忆三角函数的诱导公式一,能理解公式一的推导过程,并能应用公式一求解三角函数值。 评价目标: 为目标1.的达成做好铺垫。提升学生的数学运算的核心素养。内容3. (创设情境) 角与α的终边 有何位置关系 角 -α与α的终边 有何位置关系 角与α的终边 有何位置关系 已知任意角α的终边与单位圆相交于点P(x, y),请同学们思考回答点P关于原点、x轴、y轴对称的三个点的坐标是什么 教师:适时的引导学生思考。学生任务3.回答左边的问题 学生学习活动:自主思考,合作探究,进而解决问题设计意图: 通过完成任务3,学生会发现角的终边的对称关系,并会求关于原点、x轴及y轴对称的点的坐标。 评价目标: 为目标1.的达成奠定思维基础。提升学生的逻辑推理的核心素养。 环 节 二 探 究 新 知 内容4. 如图, 角的三角函数值与的三角函数值之间有什么关系? 教师:适时的引导学生思考,分析、解决问题。学生任务4.回答左边的问题 学生学习活动:自主思考,合作探究,进而分析问题、解决问题 提示:角π + 与角 的终边关于原点O对称, , 得出诱导公式二: sin(π + ) = sin , cos(π + ) = cos , tan(π + ) = tan 。设计意图: 通过完成任务4,学生能探究出诱导公式二,锻炼了学生分析问题、解决问题的能力。 评价目标: 达成了学习目标1.诱导公式二的探究。发展了学生直观想象、逻辑推理的数学学科核心素养。内容5. 角与的三角函数值之间有什么关系? 教师:适时的引导学生思考,分析、解决问题。学生任务5.回答左边的问题 学生学习活动:自主思考,合作探究,进而分析问题、解决问题 提示:角 与角 的终边关于x轴对称,类比公式二的探究, 得出诱导公式三: sin() = sin , cos() = cos , tan() = tan 。设计意图: 通过完成任务5,学生能探究出诱导公式三,锻炼了学生分析问题、解决问题的能力。发展了学生直观想象、逻辑推理的数学学科核心素养。 评价目标: 达成了学习目标1.诱导公式三的探究。发展了学生直观想象、逻辑推理的数学学科核心素养。内容6. 角与的三角函数值之间有什么关系? 教师:适时的引导学生思考,分析、解决问题。学生任务6.回答左边的问题 学生学习活动:自主思考,合作探究,进而分析问题、解决问题 提示:角与角的终边关于轴对称,类比公式二、三的探究过程,得出诱导公式四: sin(π - ) = sin , cos(π-)= cos , tan(π-)= -tan 。设计意图: 通过完成任务6,学生能探究出诱导公式四,锻炼了学生分析问题、解决问题的能力,发展了学生直观想象、逻辑推理的数学学科核心素养。评价目标: 达成了学习目标1.诱导公式四的探究。发展了学生直观想象、逻辑推理的数学学科核心素养。内容7.这四个诱导公式有什么规律? 教师:适时的引导学生思考,分析、解决问题。学生任务7.回答左边的问题 学生学习活动:自主思考,合作探究,分析问题、解决问题。 的三角函数值,等于的同名函数值,前面加上一个把看成锐角时原函数值的符号. 总结为一句话:函数名不变,符号看象限。设计意图: 通过完成任务7.学生能更准确的记忆诱导公式,同时培养了学生发现事物共性的能力。 评价目标: 通过总结目标1.的成果,为目标2.目标3.的达成做好了铺垫。内容8. 任意角的三角函数化为锐角三角函数的步骤? 教师:适时的引导学生思考,分析、解决问题。学生任务8.回答左边的问题 学生学习活动:自主思考,合作探究,分析问题、解决问题。 利用公式一~四把任意角的三角函数转化为锐角的三角函数,一般可按下列步骤进行: 上述步骤体现了由未知转化为已知的转化与化归的思想方法.设计意图: 通过完成任务8,学生会把任意角的三角函数化为锐角三角函数,培养了学生分析问题、解决问题的能力。 评价目标: 通过完成任务8,达成了学习目标2.的思维基础。发展了学生逻辑推理的核心素养。 环 节 三 例 题 分 析内容9.例题分析 例1 利用公式求下列三角函数值: 例2 化简 学生任务9.回答左边的问题 学生学习活动:自主思考,合作探究,分析问题、解决问题。 解: 解: , 所以 原式设计意图: 通过任务9的完成,学生能将任意角的三角函数化为锐角三角函数,能应用诱导公式一~四进行三角式的化简、求值。 评价目标: 通过完成任务9, 达成了学习目标2.学习目标3。发展了逻辑推理、数学运算的数学学科核心素养。 课 堂 检 测化简: 2.填表:
设计意图: 通过课堂检测,学生能进一步巩固诱导公式的综合应用,并检测自己完成的情况,提高了发现问题、提出问题、分析问题、解决问题的能力,评价目标: 通过课堂检测,更加确保了目标1.~目标3.的达成。发展了逻辑推理、数学运算学科核心素养。 课 堂 小 结 设计意图: 通过总结,学生进一步巩固了诱导公式及其应用,提高了自身的概括能力。 评价目标: 通过总结,学生再次明确了目标1.~目标3.的达成。
板书设计
三 三角函数的诱导公式第1课时 诱 诱导公式一 诱 诱导公式二 诱导公式三 诱导公式四例题分析 课堂小结
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
