初中数学沪教版(五四学制)(2024)七年级下册 17.2 三角形的内角和小节复习题(含解析)
文档属性
| 名称 | 初中数学沪教版(五四学制)(2024)七年级下册 17.2 三角形的内角和小节复习题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-15 15:41:44 | ||
图片预览


文档简介
17.2 三角形的内角和小节复习题
题型一 三角形的内角和定理的应用
1.在 ABC中,已知,,那么 .
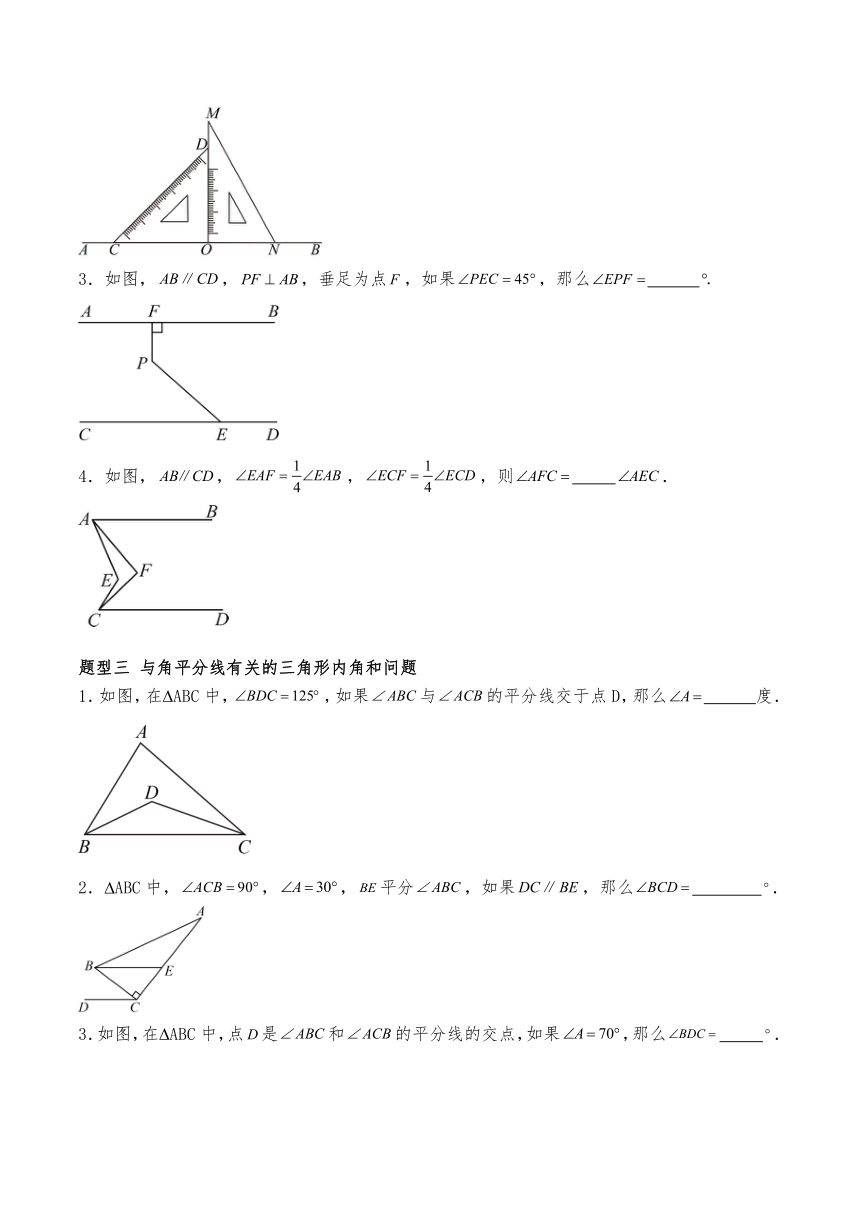
2.如图,在 ABC中,,,,则 .
3.在 ABC中,如果,,那么按角分类, ABC是 三角形.
4.如图,,,,则 .
题型二 与平行线有关的三角形内角和问题
1.如图,已知,,,,那么 .
2.如图,将一副直角三角板放在同一条直线上,其中.将三角尺绕点O以每秒的速度顺时针方向旋转一周,设旋转的时间为t秒.在旋转的过程中,边恰好与边平行,t的值为 .
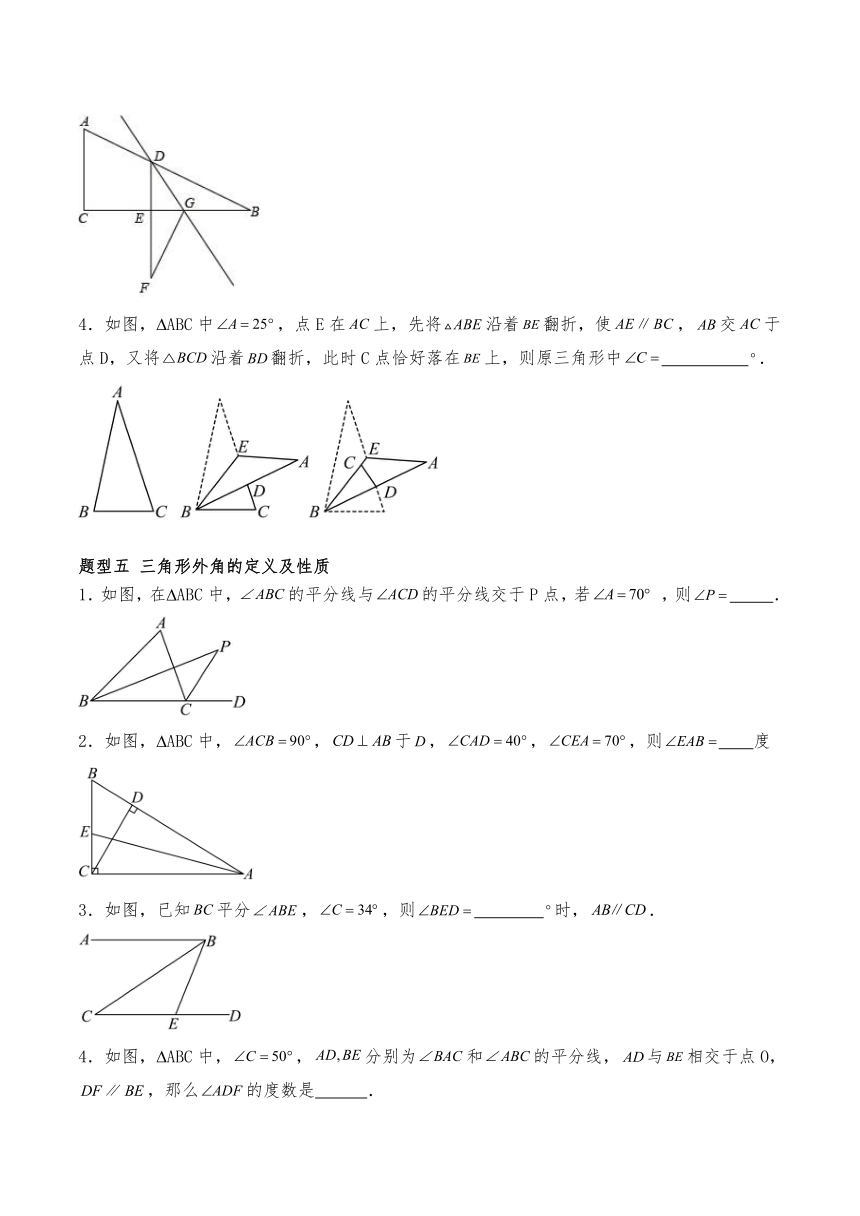
3.如图,,,垂足为点,如果,那么
4.如图,,,,则 .
题型三 与角平分线有关的三角形内角和问题
1.如图,在 ABC中,,如果与的平分线交于点D,那么 度.
2. ABC中,,,平分,如果,那么 .
3.如图,在 ABC中,点是和的平分线的交点,如果,那么 .
4.如图所示,在中,,,是角平分线,则 .
题型四 三角形折叠中的角度问题
1.如图,在锐角 ABC中,D、E分别是边和上的点,将这个纸片沿折叠,点A落在点F的位置.如果,,那么 .
2.如图, ABC中,,,点为边上一点,将沿直线折叠后,点落到点处,,则的度数为 .
3.如图,在直角三角形ABC中,,点D在AB上,点G在BC上,与关于直线DG对称,DF与BC交于点E,如果,那么与的数量关系是 .
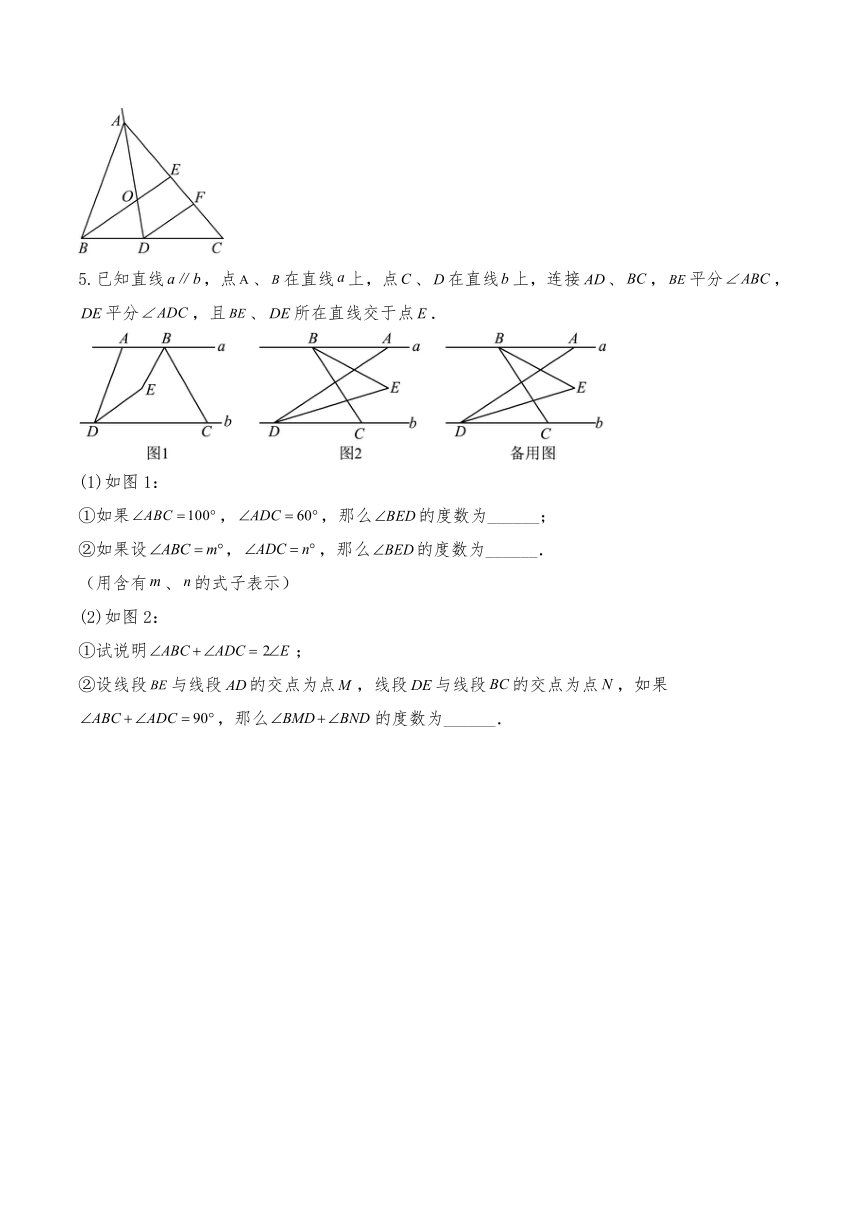
4.如图, ABC中,点E在上,先将沿着翻折,使,交于点D,又将沿着翻折,此时C点恰好落在上,则原三角形中 .
题型五 三角形外角的定义及性质
1.如图,在 ABC中,的平分线与的平分线交于P点,若 ,则 .
2.如图, ABC中,,于,,,则 度
3.如图,已知平分,,则 时,.
4.如图, ABC中,,分别为和的平分线,与相交于点O,,那么的度数是 .
5.已知直线,点、在直线上,点、在直线上,连接、,平分,平分,且、所在直线交于点.
(1)如图1:
①如果,,那么的度数为______;
②如果设,,那么的度数为______.
(用含有、的式子表示)
(2)如图2:
①试说明;
②设线段与线段的交点为点,线段与线段的交点为点,如果,那么的度数为______.
6.在 ABC中,
(1)如图1,点,分别是,上一点,若,相交于点,请说明;
(2)如图2,若,分别是,上的高,请说明理由;
(3)如图3,若,,的角平分线,,相交于点,则:
① ;
②若过点作于点,发现,请说明理由.
7.如图所示,射线CBOA,∠C=∠OAB,E、F在BC上,且满足∠EOB=∠AOB,OF平分∠COE,∠COA=80°.
(1)求∠FOB的度数;
(2)直接写出∠OBC和∠OEC的角度的数量关系;
(3)在平行移动AB的过程当中,是否存在某种情况,使∠OFC=∠OBA?若存在,直接写出其度数;若不存在,说明理由.
8.如图1,直线,直线分别交、于、点,,点在线段上(不在端点处),点在直线上,点在直线上,连接、.
(1)如图1,点在线段上,若,,则的度数为________;
(2)如图2,点在线段上,点为直线与之间区域的一点,点在线段上(不与端点重合),连、.若,,,求的度数;
(3)如图3,于点,,点在射线上运动不与重合),与的角平分线所在直线交于点,与的角平分线所在直线交于点,与的角平分线交于点,直接写出、与的数量关系.
参考答案
题型一 三角形的内角和定理的应用
1.
【分析】本题考查三角形的内角和定理,熟记任意三角形的内角和是是解题关键.
根据三角形内角和为定理进行求解.
【详解】∵,,
∴.
故答案为:.
2.
【分析】此题主要考查三角形内角和定理,熟记三角形内角和定理是解决问题的关键.由求得,可推出,再利用三角形内角和定理即可求出的度数.
【详解】解:∵,
∴,
∵,
∵,
∴,
∴,
故答案为:.
3.钝角
【分析】本题考查了三角形的内角和定理以及钝角三角形的定义,熟记三角形的内角和定理是解本题的关键.根据三角形的内角和定理,求出∠A,再判断三角形的形状.
【详解】解:∵ ABC中,如果,,,
∴,
∴三角形是钝角三角形.
故答案为:钝角.
4.118
【分析】本题考查了三角形的内角和定理以及平行线的性质,熟练掌握三角形的内角和定理是解题的关键.
延长交于点F,根据补角求得,再利用三角形内角和定理求得,再利用平行线的性质求得.
【详解】解:延长交于点F,如图所示,
∵,
∴,
∴,
∵,
∴,
∵,
∴.
故答案为:118.
题型二 与平行线有关的三角形内角和问题
1.
【分析】此题考查了三角形内角和定理,平行线的性质,
首先根据三角形内角和定理得到,然后由平行线的性质得到,然后根据三角形内角和定理求解即可.
【详解】∵,,
∴,
∵,
∴,
∵,
∴.
故答案为:.
2.或
【分析】本题考查了旋转性质以及平行线的性质,三角形的内角和为180度,先根据旋转的方向,再逐一把满足条件的图作出来,再结合图形以及运用平行线的性质列式计算,即可作答.
【详解】解:如图:
当与边平行时,
∵,
∴,,
∴,
即,
∵将三角尺绕点O以每秒的速度顺时针方向旋转一周,设旋转的时间为t秒.
∴,
∴;
如图:
当与边平行时,
∵,
∴,,
∴,
即,
∵将三角尺绕点O以每秒的速度顺时针方向旋转一周,设旋转的时间为t秒.
∴,
∴;
综上:边恰好与边平行,t的值为或
故答案为:10.5或28.5
3.
【分析】延长交于,由平行线的性质得到,求出,由邻补角的性质即可求解.
【详解】解:延长交于,
,,
,
,
,
,
,
故答案为:.
4.
【分析】本题主要考查平行线的以及角的和差计算,连接,设,,,,由平行线的性质得,进一步得出,从而可得结论
【详解】解:连接,如图,
,
设,,,,
∵
∴,
∴,
∴,
∴,
∴
;
,
∴
故答案为:
题型三 与角平分线有关的三角形内角和问题
1.
【分析】本题考查了三角形角平分线的定义、三角形内角和定理.根据三角形内角和定理可求得,从而可求,再根据三角形内角和定理可求解.
【详解】解:∵,
,
与的平分线相交于点,
,,
,
,
.
故答案为:.
2.30
【分析】此题考查了三角形内角和定理,角平分线的概念,平行线的性质,
首先根据三角形内角和定理得到,然后由角平分线的概念得到,然后根据平行线的性质求解即可.
【详解】∵,,
∴
∵平分,
∴
∵
∴.
故答案为:30.
3.125
【分析】本题考查了角平分线的性质和三角形的内角和定理,由三角形内角和定理得,由角平分线得,即可求解;掌握角平分线的性质和三角形的内角和定理是解题的关键.
【详解】解:,
,
与的平分线相交于,
,
.
故答案为:125.
4.60
【分析】依据三角形内角和定理可得,再根据BD是的平分线,可得,依据三角形内角和定理,即可得到进而求解即可.
【详解】解:∵,,
∴.
又∵BD是的平分线,
∴,
∴,
∴.
故答案为60.
题型四 三角形折叠中的角度问题
1.
【分析】本题考查的是翻折问题和三角形内角和定理,先根据平行线的性质求出的度数,再由求出的度数,根据翻折变换的性质求出的度数,根据三角形内角和定理即可得出的度数.
【详解】解:∵,
∴.
∵由翻折而成,
∴,.
∵,
∴,
∴,
∴.
故答案为:55°.
2.
【分析】根据三角形的内角和定理得到,进而求出,由折叠的性质得到,,即可求出的度数.
【详解】解:,,
,
∵∠BAE=30 ,
,
由折叠的性质得,,
,
故答案为:.
3.解:的数量关系是:.
∵,,
∴,
∴.
由翻折可得:,
∴,
∴.
故答案为:.
4.80
【分析】本题考查了折叠的性质,平行线的性质,三角形内角和定理,熟练掌握折叠的性质是解题的关键.
根据折叠的性质得出,再根据,即可得到,然后利用三角形内角和定理即可求解.
【详解】解:如图,
由折叠可得,,
∵,
∴,
∴原三角形的,
故答案为:80.
题型五 三角形外角的定义及性质
1.
【分析】本题利用了角平分线定义、三角形外角性质.利用角平分线定义可知.再利用外角性质,可得,,那么可利用,可得相等关系,从而可求.
【详解】解:∵是的角平分线,是的角平分线
∴.
又∵,
∴,
又∵,
∴,
∴.
故答案为:.
2.
【分析】本题考查了直角三角形两锐角互余的性质.根据直角三角形两锐角互余求出,然后根据代入数据进行计算即可得解.
【详解】
解:,,
,
又,
.
故答案为:.
3.
【分析】本题考查了角平分线的定义,三角形的外角的性质,平行线的判定定理,平行线的性质;根据三角形的外角的性质得,根据当时,即可求解.
【详解】解:平分,
,
设,
∵,
当时,
∴,
∴,
∴ ,
故答案为:.
4.
【分析】本题考查与角平分线有关的三角形的内角和问题,三角形的外角,以及平行线的性质,根据角平分线的性质,三角形的内角和定理以及三角形的外角求出的度数,再根据平行线的性质,求出的度数即可.
【详解】解:∵,
∴,
∵分别为和的平分线,
∴,
∴,
∴,
∵,
∴,
故答案为:.
5.(1)解:①如下图,过点作,
∵,平分,
∴,
∵,
∴,
∵,平分,
∴,
∵,,
∴,
∴,
∴;
②如下图,过点作,
∵,平分,
∴,
∵,
∴,
∵,平分,
∴,
∵,,
∴,
∴,
∴.
故答案为:①;②;
(2)①证明:如下图,过点作,
∵平分,
∴,
∵,
∴,
∵平分,
∴,
∵,,
∴,
∴,
∴,
∴;
②如下图,
∵,
∴,,
∵平分,
∴,
∴,
∵平分,
∴,
∴,
∵,
∴.
故答案为:.
6.(1)证明: 如图1,连接并延长至,
是的外角,
,
同理可得,,
;
(2)证明如图2,,分别是,上的高,
和是直角三角形,
,
;
(3)解:①如图3,
,,的角平分线,,相交于点,
,,,
,
故答案为:;
②是的外角,
,
平分,
,
,
中,,
.
7.(1)∵CB∥OA,∠C=∠OAB=100°,
∴∠COA=180°﹣∠C=180°﹣100°=80°,
∵CB∥OA,
∴∠EBO=∠AOB,
又∵∠EOB=∠AOB,
∴∠EBO=∠EOB,
∴OB平分∠AOE,
又∵OF平分∠COE,
∴∠FOB=∠EOF+∠EOB= ∠COA= ×80°=40°;
(2)结论:∠OEC=2∠OBC.
∵CB∥OA,则∠OBC=∠BOA,∠OEC=∠EOA,
则∠OBC:∠OEC=∠AOB:∠EOA,
又∵∠EOA=∠EOB+∠AOB=2∠AOB,
∴∠OBC:∠OEC=∠AOB:∠EOA=∠AOB:2∠AOB=1:2,
∴∠OEC=2∠OBC.
(3)存在
在△COF和△AOB中,
∵∠OFC=∠OBA,∠C=∠OAB,
∴∠COF=∠AOB,
∴OB、OF、OE是∠AOC的四等分线,
∴∠COF= ∠AOC= ×80°=20°,
∴∠OFC=180°﹣∠C﹣∠COF=180°﹣100°﹣20°=60°,
故存在某种情况,使∠OFC=∠OBA,此时∠OFC=∠OBA=60°.
8.(1)解:设延长线交于点,
,,
,
,
是直角三角形,
,
故答案为:;
(2)解:过点作交于点,
,,
设,,
,,,
,,
,,
,
即,
的度数为;
(3)解:当C在线段上时,过点作交于点,
在四边形中,,
与的角平分线所在直线交于点,与的角平分线所在直线交于点,与的角平分线交于点,
,,
,
,
在四边形中,,
,
即,
,
即;
当C在射线上时,过点作交于点,
,
与的角平分线所在直线交于点,与的角平分线所在直线交于点,与的角平分线交于点,
,,
,
,
在和中,,
,
即,
,
即.
题型一 三角形的内角和定理的应用
1.在 ABC中,已知,,那么 .
2.如图,在 ABC中,,,,则 .
3.在 ABC中,如果,,那么按角分类, ABC是 三角形.
4.如图,,,,则 .
题型二 与平行线有关的三角形内角和问题
1.如图,已知,,,,那么 .
2.如图,将一副直角三角板放在同一条直线上,其中.将三角尺绕点O以每秒的速度顺时针方向旋转一周,设旋转的时间为t秒.在旋转的过程中,边恰好与边平行,t的值为 .
3.如图,,,垂足为点,如果,那么
4.如图,,,,则 .
题型三 与角平分线有关的三角形内角和问题
1.如图,在 ABC中,,如果与的平分线交于点D,那么 度.
2. ABC中,,,平分,如果,那么 .
3.如图,在 ABC中,点是和的平分线的交点,如果,那么 .
4.如图所示,在中,,,是角平分线,则 .
题型四 三角形折叠中的角度问题
1.如图,在锐角 ABC中,D、E分别是边和上的点,将这个纸片沿折叠,点A落在点F的位置.如果,,那么 .
2.如图, ABC中,,,点为边上一点,将沿直线折叠后,点落到点处,,则的度数为 .
3.如图,在直角三角形ABC中,,点D在AB上,点G在BC上,与关于直线DG对称,DF与BC交于点E,如果,那么与的数量关系是 .
4.如图, ABC中,点E在上,先将沿着翻折,使,交于点D,又将沿着翻折,此时C点恰好落在上,则原三角形中 .
题型五 三角形外角的定义及性质
1.如图,在 ABC中,的平分线与的平分线交于P点,若 ,则 .
2.如图, ABC中,,于,,,则 度
3.如图,已知平分,,则 时,.
4.如图, ABC中,,分别为和的平分线,与相交于点O,,那么的度数是 .
5.已知直线,点、在直线上,点、在直线上,连接、,平分,平分,且、所在直线交于点.
(1)如图1:
①如果,,那么的度数为______;
②如果设,,那么的度数为______.
(用含有、的式子表示)
(2)如图2:
①试说明;
②设线段与线段的交点为点,线段与线段的交点为点,如果,那么的度数为______.
6.在 ABC中,
(1)如图1,点,分别是,上一点,若,相交于点,请说明;
(2)如图2,若,分别是,上的高,请说明理由;
(3)如图3,若,,的角平分线,,相交于点,则:
① ;
②若过点作于点,发现,请说明理由.
7.如图所示,射线CBOA,∠C=∠OAB,E、F在BC上,且满足∠EOB=∠AOB,OF平分∠COE,∠COA=80°.
(1)求∠FOB的度数;
(2)直接写出∠OBC和∠OEC的角度的数量关系;
(3)在平行移动AB的过程当中,是否存在某种情况,使∠OFC=∠OBA?若存在,直接写出其度数;若不存在,说明理由.
8.如图1,直线,直线分别交、于、点,,点在线段上(不在端点处),点在直线上,点在直线上,连接、.
(1)如图1,点在线段上,若,,则的度数为________;
(2)如图2,点在线段上,点为直线与之间区域的一点,点在线段上(不与端点重合),连、.若,,,求的度数;
(3)如图3,于点,,点在射线上运动不与重合),与的角平分线所在直线交于点,与的角平分线所在直线交于点,与的角平分线交于点,直接写出、与的数量关系.
参考答案
题型一 三角形的内角和定理的应用
1.
【分析】本题考查三角形的内角和定理,熟记任意三角形的内角和是是解题关键.
根据三角形内角和为定理进行求解.
【详解】∵,,
∴.
故答案为:.
2.
【分析】此题主要考查三角形内角和定理,熟记三角形内角和定理是解决问题的关键.由求得,可推出,再利用三角形内角和定理即可求出的度数.
【详解】解:∵,
∴,
∵,
∵,
∴,
∴,
故答案为:.
3.钝角
【分析】本题考查了三角形的内角和定理以及钝角三角形的定义,熟记三角形的内角和定理是解本题的关键.根据三角形的内角和定理,求出∠A,再判断三角形的形状.
【详解】解:∵ ABC中,如果,,,
∴,
∴三角形是钝角三角形.
故答案为:钝角.
4.118
【分析】本题考查了三角形的内角和定理以及平行线的性质,熟练掌握三角形的内角和定理是解题的关键.
延长交于点F,根据补角求得,再利用三角形内角和定理求得,再利用平行线的性质求得.
【详解】解:延长交于点F,如图所示,
∵,
∴,
∴,
∵,
∴,
∵,
∴.
故答案为:118.
题型二 与平行线有关的三角形内角和问题
1.
【分析】此题考查了三角形内角和定理,平行线的性质,
首先根据三角形内角和定理得到,然后由平行线的性质得到,然后根据三角形内角和定理求解即可.
【详解】∵,,
∴,
∵,
∴,
∵,
∴.
故答案为:.
2.或
【分析】本题考查了旋转性质以及平行线的性质,三角形的内角和为180度,先根据旋转的方向,再逐一把满足条件的图作出来,再结合图形以及运用平行线的性质列式计算,即可作答.
【详解】解:如图:
当与边平行时,
∵,
∴,,
∴,
即,
∵将三角尺绕点O以每秒的速度顺时针方向旋转一周,设旋转的时间为t秒.
∴,
∴;
如图:
当与边平行时,
∵,
∴,,
∴,
即,
∵将三角尺绕点O以每秒的速度顺时针方向旋转一周,设旋转的时间为t秒.
∴,
∴;
综上:边恰好与边平行,t的值为或
故答案为:10.5或28.5
3.
【分析】延长交于,由平行线的性质得到,求出,由邻补角的性质即可求解.
【详解】解:延长交于,
,,
,
,
,
,
,
故答案为:.
4.
【分析】本题主要考查平行线的以及角的和差计算,连接,设,,,,由平行线的性质得,进一步得出,从而可得结论
【详解】解:连接,如图,
,
设,,,,
∵
∴,
∴,
∴,
∴,
∴
;
,
∴
故答案为:
题型三 与角平分线有关的三角形内角和问题
1.
【分析】本题考查了三角形角平分线的定义、三角形内角和定理.根据三角形内角和定理可求得,从而可求,再根据三角形内角和定理可求解.
【详解】解:∵,
,
与的平分线相交于点,
,,
,
,
.
故答案为:.
2.30
【分析】此题考查了三角形内角和定理,角平分线的概念,平行线的性质,
首先根据三角形内角和定理得到,然后由角平分线的概念得到,然后根据平行线的性质求解即可.
【详解】∵,,
∴
∵平分,
∴
∵
∴.
故答案为:30.
3.125
【分析】本题考查了角平分线的性质和三角形的内角和定理,由三角形内角和定理得,由角平分线得,即可求解;掌握角平分线的性质和三角形的内角和定理是解题的关键.
【详解】解:,
,
与的平分线相交于,
,
.
故答案为:125.
4.60
【分析】依据三角形内角和定理可得,再根据BD是的平分线,可得,依据三角形内角和定理,即可得到进而求解即可.
【详解】解:∵,,
∴.
又∵BD是的平分线,
∴,
∴,
∴.
故答案为60.
题型四 三角形折叠中的角度问题
1.
【分析】本题考查的是翻折问题和三角形内角和定理,先根据平行线的性质求出的度数,再由求出的度数,根据翻折变换的性质求出的度数,根据三角形内角和定理即可得出的度数.
【详解】解:∵,
∴.
∵由翻折而成,
∴,.
∵,
∴,
∴,
∴.
故答案为:55°.
2.
【分析】根据三角形的内角和定理得到,进而求出,由折叠的性质得到,,即可求出的度数.
【详解】解:,,
,
∵∠BAE=30 ,
,
由折叠的性质得,,
,
故答案为:.
3.解:的数量关系是:.
∵,,
∴,
∴.
由翻折可得:,
∴,
∴.
故答案为:.
4.80
【分析】本题考查了折叠的性质,平行线的性质,三角形内角和定理,熟练掌握折叠的性质是解题的关键.
根据折叠的性质得出,再根据,即可得到,然后利用三角形内角和定理即可求解.
【详解】解:如图,
由折叠可得,,
∵,
∴,
∴原三角形的,
故答案为:80.
题型五 三角形外角的定义及性质
1.
【分析】本题利用了角平分线定义、三角形外角性质.利用角平分线定义可知.再利用外角性质,可得,,那么可利用,可得相等关系,从而可求.
【详解】解:∵是的角平分线,是的角平分线
∴.
又∵,
∴,
又∵,
∴,
∴.
故答案为:.
2.
【分析】本题考查了直角三角形两锐角互余的性质.根据直角三角形两锐角互余求出,然后根据代入数据进行计算即可得解.
【详解】
解:,,
,
又,
.
故答案为:.
3.
【分析】本题考查了角平分线的定义,三角形的外角的性质,平行线的判定定理,平行线的性质;根据三角形的外角的性质得,根据当时,即可求解.
【详解】解:平分,
,
设,
∵,
当时,
∴,
∴,
∴ ,
故答案为:.
4.
【分析】本题考查与角平分线有关的三角形的内角和问题,三角形的外角,以及平行线的性质,根据角平分线的性质,三角形的内角和定理以及三角形的外角求出的度数,再根据平行线的性质,求出的度数即可.
【详解】解:∵,
∴,
∵分别为和的平分线,
∴,
∴,
∴,
∵,
∴,
故答案为:.
5.(1)解:①如下图,过点作,
∵,平分,
∴,
∵,
∴,
∵,平分,
∴,
∵,,
∴,
∴,
∴;
②如下图,过点作,
∵,平分,
∴,
∵,
∴,
∵,平分,
∴,
∵,,
∴,
∴,
∴.
故答案为:①;②;
(2)①证明:如下图,过点作,
∵平分,
∴,
∵,
∴,
∵平分,
∴,
∵,,
∴,
∴,
∴,
∴;
②如下图,
∵,
∴,,
∵平分,
∴,
∴,
∵平分,
∴,
∴,
∵,
∴.
故答案为:.
6.(1)证明: 如图1,连接并延长至,
是的外角,
,
同理可得,,
;
(2)证明如图2,,分别是,上的高,
和是直角三角形,
,
;
(3)解:①如图3,
,,的角平分线,,相交于点,
,,,
,
故答案为:;
②是的外角,
,
平分,
,
,
中,,
.
7.(1)∵CB∥OA,∠C=∠OAB=100°,
∴∠COA=180°﹣∠C=180°﹣100°=80°,
∵CB∥OA,
∴∠EBO=∠AOB,
又∵∠EOB=∠AOB,
∴∠EBO=∠EOB,
∴OB平分∠AOE,
又∵OF平分∠COE,
∴∠FOB=∠EOF+∠EOB= ∠COA= ×80°=40°;
(2)结论:∠OEC=2∠OBC.
∵CB∥OA,则∠OBC=∠BOA,∠OEC=∠EOA,
则∠OBC:∠OEC=∠AOB:∠EOA,
又∵∠EOA=∠EOB+∠AOB=2∠AOB,
∴∠OBC:∠OEC=∠AOB:∠EOA=∠AOB:2∠AOB=1:2,
∴∠OEC=2∠OBC.
(3)存在
在△COF和△AOB中,
∵∠OFC=∠OBA,∠C=∠OAB,
∴∠COF=∠AOB,
∴OB、OF、OE是∠AOC的四等分线,
∴∠COF= ∠AOC= ×80°=20°,
∴∠OFC=180°﹣∠C﹣∠COF=180°﹣100°﹣20°=60°,
故存在某种情况,使∠OFC=∠OBA,此时∠OFC=∠OBA=60°.
8.(1)解:设延长线交于点,
,,
,
,
是直角三角形,
,
故答案为:;
(2)解:过点作交于点,
,,
设,,
,,,
,,
,,
,
即,
的度数为;
(3)解:当C在线段上时,过点作交于点,
在四边形中,,
与的角平分线所在直线交于点,与的角平分线所在直线交于点,与的角平分线交于点,
,,
,
,
在四边形中,,
,
即,
,
即;
当C在射线上时,过点作交于点,
,
与的角平分线所在直线交于点,与的角平分线所在直线交于点,与的角平分线交于点,
,,
,
,
在和中,,
,
即,
,
即.
同课章节目录
