初中数学沪教版(五四学制)(2024)七年级下册 17.4 三角形全等的判定小节复习题(含答案)
文档属性
| 名称 | 初中数学沪教版(五四学制)(2024)七年级下册 17.4 三角形全等的判定小节复习题(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-15 15:43:34 | ||
图片预览



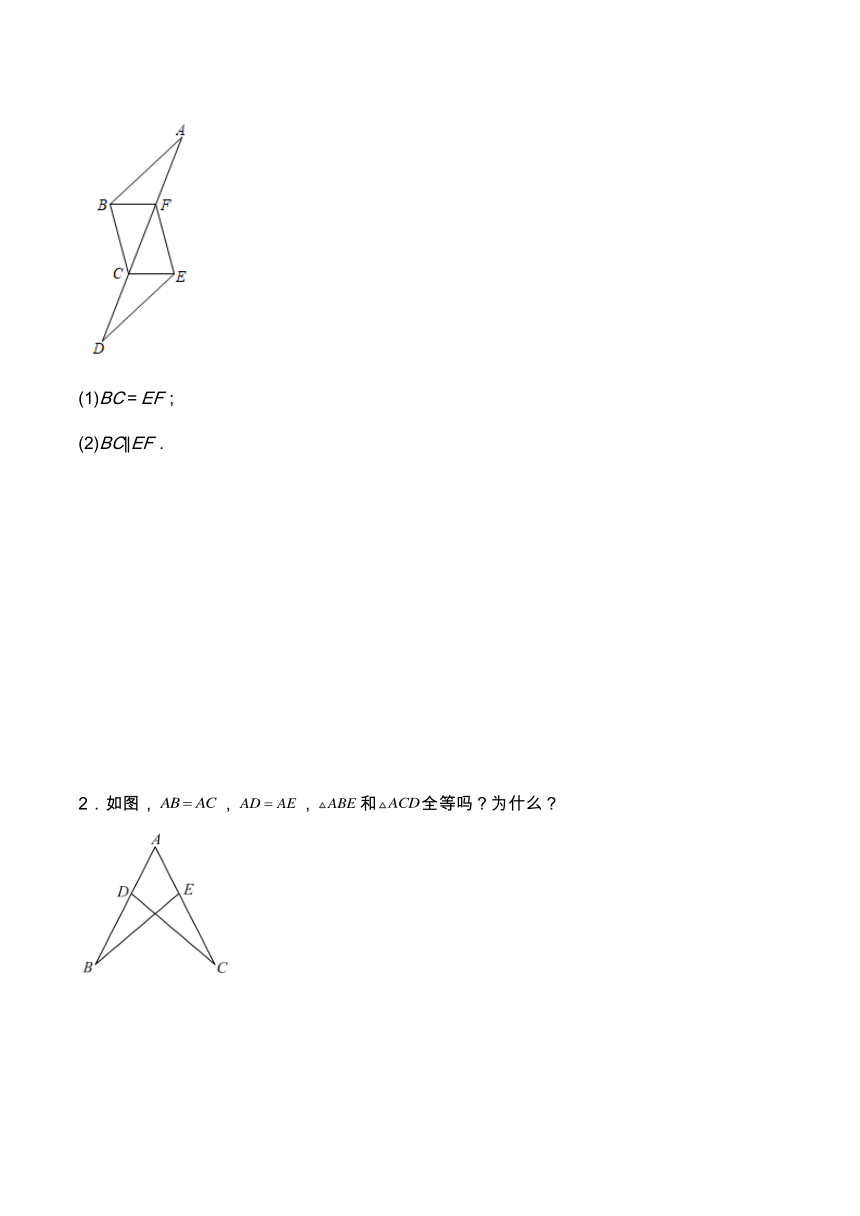

文档简介
17.4 三角形全等的判定小节复习题
题型一 用SSS证明三角形全等
1.已知:如图,点C、D在的异侧,,,请说明 ABC与全等的理由.
2.如图,点B,E,C,F在一条直线上,,,,
(1)求证:
(2)若,,求的度数
3.如图,点在一条直线上,,求证:.
4.如图,在四边形中,,连接,试说明.
题型二 用SAS证明三角形全等
1.已知:如图,A、F、C、D在同一直线上,AB∥DE,AB=DE,AF=CD,求证:
(1)BC=EF;
(2)BC∥EF.
2.如图,,,和全等吗?为什么?
3.如图,已知点B,E,C,F在一条直线上,,,.试说明:.
4.如图,已知A、B、C、D在同一直线上,,,且,
求证:.
题型三 用ASA或AAS证明三角形全等
1.如图,在△ABC中,已知∠ABC=∠ACB,BD、CE分别平分∠ABC、∠ACB,那么△BDC与△CEB全等吗?为什么?
解:因为BD、CE分别平分∠ABC、∠ACB(已知),
所以∠DBC=( ),∠ECB=( ).
由∠ABC=∠ACB(已知),
所以∠DBC=∠ECB( ).
在△BDC与△CEB中,
,
( ),
( ).
所以△BDC≌△CEB(ASA).
2.如图,在中,点是边的中点,过点作直线使,交的延长线于点.试说明的理由.
解:因为(已知),
所以 ( )
因为点是边的中点,
所以
在和中,
所以( )
所以( )
3.如图,已知BE与CD相交于点O,且BO=CO,∠ADC=∠AEB,那么△BDO与△CEO全等吗?为什么?
4.如图,已知是中边上的中线,、是直线上的点,且说明和全等的理由.
题型四 用HL证明三角形全等
1.已知:如图,,,平分,.求证:平分.
2.已知:如图,AB∥CD,∠ABD=90°,∠AED=90°,BD=DE.求证:∠AFC=2∠ADC.
3.如图,已知,,,,与交于点O.
(1)求证:.
(2)求.
4.如图,在中,,直线l经过顶点C,过A,B两点分别作l的垂线,E,F为垂足,且;
求证:
(1)
(2).
题型五 倍长中线模型
1.安安同学遇到这样一个问题:如图, ABC中,,,是中线,求的取值范围.
宁宁提示她可以延长到,使,连接,证明,经过推理和计算使问题得到解决.请解答:
(1)和全等吗?请说明理由;
(2)求出的取值范围.
2.如图所示,是的边的中线.
(1)画出以点为对称中心且与成中心对称的三角形;
(2)若,,求的长的取值范围.
3.如图,在 ABC中,,
(1)求边的长的取值范围?
(2)若是 ABC的中线,求取值范围?
4.(1)如图,在中,,,点G是的中点,求中线的取值范围;
(2)如图,在四边形中,,点E是的中点.若是的平分线.试探究,,之间的等量关系,并证明你的结论.
题型六 旋转模型
1.在△ABC中,∠BAC=90°,AC=AB,直线MN经过点A,且CD⊥MN于D,BE⊥MN于E.
(1)当直线MN绕点A旋转到图1的位置时, 度;
(2)求证:DE=CD+BE;
(3)当直线MN绕点A旋转到图2的位置时,试问DE、CD、BE具有怎样的等量关系?请写出这个等量关系,并加以证明.
2.【基本模型】
(1)如图1,是正方形,,当在边上,在边上时,请你探究、与之间的数量关系,并证明你的结论.
【模型运用】
(2)如图2,是正方形,,当在的延长线上,在的延长线上时,请你探究、与之间的数量关系,并证明你的结论.
3.
如图,,,.
(1)求证:;
(2)若,试判断与的数量及位置关系并证明;
(3)若,求的度数.
4.已知:,,.
(1)如图1当点在上,______.
(2)如图2猜想与的面积有何关系?请说明理由.(温馨提示:两三角形可以看成是等底的)
题型七 垂线模型
1.如图,已知:在 ABC中,,,直线经过点,,.
(1)当直线绕点旋转到图(1)的位置时,求证:;
(2)当直线绕点旋转到图(2)的位置时,求证:;
(3)当直线绕点旋转到图(3)的位置时,试问、、具有怎样的等量关系?请直接写出这个等量关系:____________.
2.如图,三点在同一条直线上,,,.
(1)求证:;
(2)当 ABC满足__________时,?
3.如图,为等腰直角三角形,,.
(1)求证:;
(2)求证:
4.通过对下面数学模型的研究学习,解决下列问题:
【模型呈现】
某兴趣小组在从汉代数学家赵爽的弦图(如图1,由外到内含三个正方形)中提炼出两个三角形全等模型图(如图2、图3),即“一线三等角”模型和“K字”模型.
【问题发现】
(1)如图2,已知, ABC中,,,一直线过顶点C,过A,B分别作其垂线,垂足分别为E,F.求证:;
(2)如图3,若改变直线的位置,其余条件与(1)相同,请直接写出,,之间的数量关系 ;
【问题提出】
(3)在(2)的条件下,若,,则的面积为 .
(4)如图4,四边形中,,面积为18且的长为9,则的面积为 .
题型八 添加条件使三角形全等
1.如图,点A,E,F,C在同一条直线上,,,请你再添加一个条件使得,并说明理由.
2.如下图,在 ABC与中,已知.
(1)在不添加任何辅助线的前提下,下列条件:①;②;③;④.其中能使的有_______(填序号);
(2)根据(1)中添加的条件,分别说明.
3.如图,点为 ABC和 ADE的公共顶点,已知,请你添加一个条件,使得.(不再添加其他线段和字母)
(1)你添加的条件是______.
(2)根据你添加的条件,写出证明过程.
4.(23-24七年级下·江西吉安·期末)如图,在 ABC与中,已知.
(1)在不添加任何辅助线的前提下,以下条件中,能使的条件有_____(填序号),
①;②;③;④;
(2)分别对(1)中添加条件的情况证明,并指出两个三角形全等的判定方法.
题型九 全等三角形综合问题
1.如图,已知四边形ABCD中,AB∥CD,AD∥BC.E为BD上一点,且BE=AD,∠DEF=∠ADC,EF交BC的延长线于点F.
(1)AD和BC相等吗?为什么?
(2)BF和BD相等吗?为什么?
2.如图,在三角形ABC中,已知点D、E、F分别在边BC、AC、AB上,且FD=DE,BF=CD,∠FDE=∠B,那么∠B与∠C相等吗?为什么?
3.如图,已知AF与BE相交于点O,C、D分别是AF与BE上的两点,EF∥AB,并且∠A+∠ACD=180°.
(1)请说明CD∥EF的理由;
(2)分别连结CE、DF,若OE=OF,请说明△ECD≌△FDC的理由.
4.如图,四边形,点E,F在边上,满足,,.
(1)求证:.
(2)若,求的长.
参考答案
题型一 用SSS证明三角形全等
1.解:在△ABC与中,
,
∴△ABC≌△ABD(SSS).
2.(1)证明:,
,
即,
在△ABC和中,
,
.
(2)解:,,,
,
.
3.证明:∵,
∴,
即,
在和中
,
∴.
4.解: 在△ABD和△CBD中,
,
∴∠ABD≌△CBD(SSS)
题型二 用SAS证明三角形全等
1.(1)证明:(1),
,
,
,
在△ABC与 中
,
,
.
(2)(2),
,
.
2.解:,理由为:
在和中,
,
∴.
3.解:∵,
∴,
即:,
∵
∴
在△ABC和中,
∴.
4.证明:∵,
∴,
在和中,
,
∴.
题型三 用ASA或AAS证明三角形全等
1.解:△BDC与△CEB全等,
因为BD、CE分别平分∠ABC、∠ACB(已知),
所以∠DBC=(∠ABC),∠ECB=(∠ACB),
由∠ABC=∠ACB(已知),
所以∠DBC=∠ECB( 等量代换),
在△BDC与△CEB中,
,
所以△BDC≌△CEB(ASA),
故答案为:∠ABC;∠ACB;等量代换;∠DBC=∠ECB;BC=CB;公共边;∠ACB=∠ABC;已知.
2.解:因为(已知),
所以∠E(两直线平行,内错角相等)
因为点是边的中点,
所以BD=CD.
在和中,
(对顶角相等)
所以(AAS)
所以(全等三角形的对应边相等)
3.解:△BDO与△CEO全等;
∵∠BDO=180°﹣∠ADC,∠CEO=180°﹣∠AEB,
又∵∠ADC=∠AEB,
∴∠BDO=∠CEO,
∵在△BDO与△CEO中,,
∴△BDO≌△CEO(AAS).
4.证明:是△ABC中边上的中线,
,
,
,.
在与中,
,
≌.
题型四 用HL证明三角形全等
1.证明:在上取一点,使,
平分,
,
在与中,
,
,
,,,
,
∴,
,
,
在与中,
,
,
,
即平分.
2.证明:在Rt△ABD与Rt△AED中,
,
∴Rt△ABD≌Rt△AED(HL),
∴∠BAD=∠EAD,
∵AB∥CD,
∴∠BAD=∠ADC,
∴∠EAD=∠ADC,
∵∠AFC=∠EAD+∠ADC,
∴∠AFC=2∠ADC.
3.(1)证明:∵,
∴,即,
∵,
在和中,
,
∴;
(2)解:∵,,
∴,
由(1)知:,
∴,
∴,
∴,
∴的度数为.
4.(1)证明:∵于E点,于F点
∴在与中
∴
∴;
(2)证明:在直角三角形中,
∴
∴
∵E、C,F三点共线
∴
∴.
题型五 倍长中线模型
1.(1)解:∵是中线,
∴,
延长到,使,
又,
∴
(2)由(1)可知,,,
在中,,,
∴,即,
∴.
2.(1)解:如图所述,以点为对称中心旋转,得,
∴与关于点成对称中心图形.
(2)解:由(1)可知,与关于点成对称中心图形,
∴,
∴,,
在中,,即,
∴,
∵,
∴,解得,,
∴的长的取值范围.
3.(1)解:由三角形的三边关系可知:,
∵,
∴;
(2)解:延长至E,使,连接,
在中,∵,
∴,
∴,
由三角形的三边关系:,
∴,
∴.
4.(1)解:延长DG至M,使GM=DG,连接MF,
在和中,
∴(SAS),
∴DE=MF=3,
∵DF-MF<DM<DF+MF,
∴7-3<DM<7+3,
即4<DM<10,
∵,
∴4<2DG<10,
∴2<DG<5;
(2)AD=CD+AB,理由如下:
解:延长AE,DC相交于点F,
∵,
∴∠BAE=∠F,
∵点E是BC的中点,
∴BE=CE,
在和中,
∴(AAS),
∴AB=CF,
∵∠BAE=∠F,∠DAF=∠BAE,
∴∠F=∠DAF,
∴AD=FD,
∵FD=CD+CF,CF=AB,
∴AD=CD+AB.
题型六 旋转模型
1.(1)∵∠BAC=90°
∴ ∠EAB+∠DAC=180°-∠BAC=180°-90°=90°
故答案为:90°.
(2)证明:∵ CD⊥MN于D,BE⊥MN于E
∴ ∠ADC=∠BEA=∠BAC=90°
∵ ∠DAC+∠DCA=90°且 ∠DAC+∠EAB=90°
∴ ∠DCA=∠EAB
∵在△DCA和△EAB中
∴△DCA≌△EAB (AAS)
∴ AD=BE且EA=DC
由图可知:DE = EA+AD = DC+BE.
(3)∵ CD⊥MN于D,BE⊥MN于E
∴ ∠ADC=∠BEA=∠BAC=90°
∵ ∠DAC+∠DCA=90°且∠DAC+∠EAB=90°
∴ ∠DCA=∠EAB
∵在△DCA和△EAB中
∴△DCA≌△EAB (AAS)
∴ AD=BE且AE=CD
由图可知:AE = AD +DE
∴ CD= BE + DE.
2.解:(1)结论:.
理由:如图1,将绕点顺时针旋转,使与重合,得到,
则:,,,
∴,即:三点共线,
,
∴,
∴,
,
在和中,
,
,
,
又,
.
(2)结论:.
理由:如图2,将绕点顺时针旋转,使与重合,得到,
则:,
同法(1)可得:,
,
又,
.
3.(1)∵∠CAB=∠EAD
∴∠CAB+∠BAE=∠EAD+∠BAE,
∴ ∠CAE=∠BAD,
∵AB=AC,AE=AD
在△AEC和△ADB中
∴ △AEC≌△ADB(SAS)
(2)CE=BD且CE⊥BD,证明如下:
将直线CE与AB的交点记为点O,
由(1)可知△AEC≌△ADB,
∴ CE=BD, ∠ACE=∠ABD,
∵∠BOF=∠AOC,∠=90°,
∴ ∠BFO=∠CAB=∠=90°,
∴ CE⊥BD.
(3)过A分别做AM⊥CE,AN⊥BD
由(1)知△AEC≌△ADB,
∴两个三角形面积相等
故AM·CE=AN·BD
∴AM=AN
∴AF平分∠DFC
由(2)可知∠BFC=∠BAC=
∴∠DFC=180°-
∴∠CFA=∠DFC=
4.(1)解:,
,
又,,
,
在中,,
故答案为:.
(2)解:如下图所示:过点作的边上的高,过点作的边上的高,由作图及知:
,,,
(同角的余角相等),
在与中有:
(),
,
,,
,,
,
故答案为:.
题型七 垂线模型
1.解:(1)证明:如图1,
∵AD⊥DE,BE⊥DE,
∴∠ADC=∠BEC=90°,
∵∠ACB=90°,
∴∠ACD+∠BCE=90°,∠DAC+∠ACD=90°,
∴∠DAC=∠BCE,
在△ADC和△CEB中,
,
∴△ADC≌△CEB(AAS);
(2)如图2,∵BE⊥EC,AD⊥CE,
∴∠ADC=∠BEC=90°,
∴∠EBC+∠ECB=90°,
∵∠ACB=90°,
∴∠ECB+∠ACE=90°,
∴∠ACD=∠EBC,
在△ADC和△CEB中,
,
∴△ADC≌△CEB(AAS),
∴AD=CE,CD=BE,
∴DE=EC-CD=AD-BE.
(3)DE=BE-AD;
如图3,∵∠ACB=90°,
∴∠ACD+∠BCE=90°
∵AD⊥MN,BE⊥MN,
∴∠ADC=∠CEB=90°,
∴∠ACD+∠DAC=90°,
∴∠DAC=∠ECB,
在△ACD和△CBE中,
,
∴△ACD≌△CBE(AAS),
∴AD=CE,CD=BE,
∴DE=CD-CE=BE-AD.
2.(1)证明:在△ABC和中
,
∴;
∴,
∵,
∴.
(2)解:当时,.理由如下:
∵,
∴,
∵,
∴.
∴.
∴.
3.(1)证明:是等腰直角三角形,
∴,
∵,
∴,
∴,
在△BC与△BDE中,
,
∴
(2)证明:∵,
∴,
∵,
∴,
∴,
∴,
∴.
4.(1)证明:由题意可得,,
∴,,
∵,
∴,
∴,
在和中,
∴
∴,,
∴;
(2),
证明:由题意可得,,
∴,,
∵,
∴,
∴,
在和中,
∴
∴,,
∴;
(3)设,则,
∴
∵,
∴
∴;
(4)如图,过点B作交的延长线于点E,过点F作于点F,
由(1)可得
∴,,
∵,
∴是等腰直角三角形,
∴,
∵面积为18
∴
∴,
∵的长为9,
∴,
∴
题型八 添加条件使三角形全等
1.解:添加的条件为,理由如下:
因为,
所以,
即,
在和中,
,
所以.
2.(1)①③
(2)解:选①时,
在△ABC和中,
,
;
选③时,
在△ABC和中,
,
.
题型九 全等三角形综合问题
1.(1)AD=CB,
理由如下:∵AB∥CD,
∴∠ABD=∠CDB,
同理可得,∠ADB=∠CBD,
在△ABD与△CDB中,
∴△ABD≌△CDB(ASA),
∴AD=CB;
(2)BF=BD,
理由
∵AD=CB,BE=AD,
∴BC=BE,
∵AD∥BC,
∴∠ADB=∠DBF,
∵∠DEF=∠ADC,
∴∠DEF﹣∠DBF=∠ADC﹣∠ADB,
即∠EFB=∠CDB,
在△EFB与△CDB中,
,
∴△EFB≌△CDB(AAS),
∴FB=DB.
2.解:∠B与∠C相等,
理由:∵∠FDC=∠FDE+∠EDC,
又∵∠FDC=∠B+∠BFD,
∴∠FDE+∠EDC=∠B+∠BFD,
又∵∠FDE=∠B,
∴∠BFD=∠EDC,
在△BFD和△CDE中
,
∴△BFD≌△CDE(SAS),
∴∠B=∠C.
3.(1)∵∠A+∠ACD=180°,
∴,
∵,
∴.
(2)∵OE=OF,
∴∠OEF=∠OFE,
∵,
∴∠OEF=∠ODC,∠OFE=∠OCD,
∴∠ODC=∠OCD,
∴OC=OD,
∴OC+OF=OD+OE,
即CF=DE,
在△ECD和△FDC中,
,
∴△ECD≌△FDC(SAS).
4.(1)证明:,
,即,
在和中,
,
;
(2)解:,
,
在和中,
,
,
.
题型一 用SSS证明三角形全等
1.已知:如图,点C、D在的异侧,,,请说明 ABC与全等的理由.
2.如图,点B,E,C,F在一条直线上,,,,
(1)求证:
(2)若,,求的度数
3.如图,点在一条直线上,,求证:.
4.如图,在四边形中,,连接,试说明.
题型二 用SAS证明三角形全等
1.已知:如图,A、F、C、D在同一直线上,AB∥DE,AB=DE,AF=CD,求证:
(1)BC=EF;
(2)BC∥EF.
2.如图,,,和全等吗?为什么?
3.如图,已知点B,E,C,F在一条直线上,,,.试说明:.
4.如图,已知A、B、C、D在同一直线上,,,且,
求证:.
题型三 用ASA或AAS证明三角形全等
1.如图,在△ABC中,已知∠ABC=∠ACB,BD、CE分别平分∠ABC、∠ACB,那么△BDC与△CEB全等吗?为什么?
解:因为BD、CE分别平分∠ABC、∠ACB(已知),
所以∠DBC=( ),∠ECB=( ).
由∠ABC=∠ACB(已知),
所以∠DBC=∠ECB( ).
在△BDC与△CEB中,
,
( ),
( ).
所以△BDC≌△CEB(ASA).
2.如图,在中,点是边的中点,过点作直线使,交的延长线于点.试说明的理由.
解:因为(已知),
所以 ( )
因为点是边的中点,
所以
在和中,
所以( )
所以( )
3.如图,已知BE与CD相交于点O,且BO=CO,∠ADC=∠AEB,那么△BDO与△CEO全等吗?为什么?
4.如图,已知是中边上的中线,、是直线上的点,且说明和全等的理由.
题型四 用HL证明三角形全等
1.已知:如图,,,平分,.求证:平分.
2.已知:如图,AB∥CD,∠ABD=90°,∠AED=90°,BD=DE.求证:∠AFC=2∠ADC.
3.如图,已知,,,,与交于点O.
(1)求证:.
(2)求.
4.如图,在中,,直线l经过顶点C,过A,B两点分别作l的垂线,E,F为垂足,且;
求证:
(1)
(2).
题型五 倍长中线模型
1.安安同学遇到这样一个问题:如图, ABC中,,,是中线,求的取值范围.
宁宁提示她可以延长到,使,连接,证明,经过推理和计算使问题得到解决.请解答:
(1)和全等吗?请说明理由;
(2)求出的取值范围.
2.如图所示,是的边的中线.
(1)画出以点为对称中心且与成中心对称的三角形;
(2)若,,求的长的取值范围.
3.如图,在 ABC中,,
(1)求边的长的取值范围?
(2)若是 ABC的中线,求取值范围?
4.(1)如图,在中,,,点G是的中点,求中线的取值范围;
(2)如图,在四边形中,,点E是的中点.若是的平分线.试探究,,之间的等量关系,并证明你的结论.
题型六 旋转模型
1.在△ABC中,∠BAC=90°,AC=AB,直线MN经过点A,且CD⊥MN于D,BE⊥MN于E.
(1)当直线MN绕点A旋转到图1的位置时, 度;
(2)求证:DE=CD+BE;
(3)当直线MN绕点A旋转到图2的位置时,试问DE、CD、BE具有怎样的等量关系?请写出这个等量关系,并加以证明.
2.【基本模型】
(1)如图1,是正方形,,当在边上,在边上时,请你探究、与之间的数量关系,并证明你的结论.
【模型运用】
(2)如图2,是正方形,,当在的延长线上,在的延长线上时,请你探究、与之间的数量关系,并证明你的结论.
3.
如图,,,.
(1)求证:;
(2)若,试判断与的数量及位置关系并证明;
(3)若,求的度数.
4.已知:,,.
(1)如图1当点在上,______.
(2)如图2猜想与的面积有何关系?请说明理由.(温馨提示:两三角形可以看成是等底的)
题型七 垂线模型
1.如图,已知:在 ABC中,,,直线经过点,,.
(1)当直线绕点旋转到图(1)的位置时,求证:;
(2)当直线绕点旋转到图(2)的位置时,求证:;
(3)当直线绕点旋转到图(3)的位置时,试问、、具有怎样的等量关系?请直接写出这个等量关系:____________.
2.如图,三点在同一条直线上,,,.
(1)求证:;
(2)当 ABC满足__________时,?
3.如图,为等腰直角三角形,,.
(1)求证:;
(2)求证:
4.通过对下面数学模型的研究学习,解决下列问题:
【模型呈现】
某兴趣小组在从汉代数学家赵爽的弦图(如图1,由外到内含三个正方形)中提炼出两个三角形全等模型图(如图2、图3),即“一线三等角”模型和“K字”模型.
【问题发现】
(1)如图2,已知, ABC中,,,一直线过顶点C,过A,B分别作其垂线,垂足分别为E,F.求证:;
(2)如图3,若改变直线的位置,其余条件与(1)相同,请直接写出,,之间的数量关系 ;
【问题提出】
(3)在(2)的条件下,若,,则的面积为 .
(4)如图4,四边形中,,面积为18且的长为9,则的面积为 .
题型八 添加条件使三角形全等
1.如图,点A,E,F,C在同一条直线上,,,请你再添加一个条件使得,并说明理由.
2.如下图,在 ABC与中,已知.
(1)在不添加任何辅助线的前提下,下列条件:①;②;③;④.其中能使的有_______(填序号);
(2)根据(1)中添加的条件,分别说明.
3.如图,点为 ABC和 ADE的公共顶点,已知,请你添加一个条件,使得.(不再添加其他线段和字母)
(1)你添加的条件是______.
(2)根据你添加的条件,写出证明过程.
4.(23-24七年级下·江西吉安·期末)如图,在 ABC与中,已知.
(1)在不添加任何辅助线的前提下,以下条件中,能使的条件有_____(填序号),
①;②;③;④;
(2)分别对(1)中添加条件的情况证明,并指出两个三角形全等的判定方法.
题型九 全等三角形综合问题
1.如图,已知四边形ABCD中,AB∥CD,AD∥BC.E为BD上一点,且BE=AD,∠DEF=∠ADC,EF交BC的延长线于点F.
(1)AD和BC相等吗?为什么?
(2)BF和BD相等吗?为什么?
2.如图,在三角形ABC中,已知点D、E、F分别在边BC、AC、AB上,且FD=DE,BF=CD,∠FDE=∠B,那么∠B与∠C相等吗?为什么?
3.如图,已知AF与BE相交于点O,C、D分别是AF与BE上的两点,EF∥AB,并且∠A+∠ACD=180°.
(1)请说明CD∥EF的理由;
(2)分别连结CE、DF,若OE=OF,请说明△ECD≌△FDC的理由.
4.如图,四边形,点E,F在边上,满足,,.
(1)求证:.
(2)若,求的长.
参考答案
题型一 用SSS证明三角形全等
1.解:在△ABC与中,
,
∴△ABC≌△ABD(SSS).
2.(1)证明:,
,
即,
在△ABC和中,
,
.
(2)解:,,,
,
.
3.证明:∵,
∴,
即,
在和中
,
∴.
4.解: 在△ABD和△CBD中,
,
∴∠ABD≌△CBD(SSS)
题型二 用SAS证明三角形全等
1.(1)证明:(1),
,
,
,
在△ABC与 中
,
,
.
(2)(2),
,
.
2.解:,理由为:
在和中,
,
∴.
3.解:∵,
∴,
即:,
∵
∴
在△ABC和中,
∴.
4.证明:∵,
∴,
在和中,
,
∴.
题型三 用ASA或AAS证明三角形全等
1.解:△BDC与△CEB全等,
因为BD、CE分别平分∠ABC、∠ACB(已知),
所以∠DBC=(∠ABC),∠ECB=(∠ACB),
由∠ABC=∠ACB(已知),
所以∠DBC=∠ECB( 等量代换),
在△BDC与△CEB中,
,
所以△BDC≌△CEB(ASA),
故答案为:∠ABC;∠ACB;等量代换;∠DBC=∠ECB;BC=CB;公共边;∠ACB=∠ABC;已知.
2.解:因为(已知),
所以∠E(两直线平行,内错角相等)
因为点是边的中点,
所以BD=CD.
在和中,
(对顶角相等)
所以(AAS)
所以(全等三角形的对应边相等)
3.解:△BDO与△CEO全等;
∵∠BDO=180°﹣∠ADC,∠CEO=180°﹣∠AEB,
又∵∠ADC=∠AEB,
∴∠BDO=∠CEO,
∵在△BDO与△CEO中,,
∴△BDO≌△CEO(AAS).
4.证明:是△ABC中边上的中线,
,
,
,.
在与中,
,
≌.
题型四 用HL证明三角形全等
1.证明:在上取一点,使,
平分,
,
在与中,
,
,
,,,
,
∴,
,
,
在与中,
,
,
,
即平分.
2.证明:在Rt△ABD与Rt△AED中,
,
∴Rt△ABD≌Rt△AED(HL),
∴∠BAD=∠EAD,
∵AB∥CD,
∴∠BAD=∠ADC,
∴∠EAD=∠ADC,
∵∠AFC=∠EAD+∠ADC,
∴∠AFC=2∠ADC.
3.(1)证明:∵,
∴,即,
∵,
在和中,
,
∴;
(2)解:∵,,
∴,
由(1)知:,
∴,
∴,
∴,
∴的度数为.
4.(1)证明:∵于E点,于F点
∴在与中
∴
∴;
(2)证明:在直角三角形中,
∴
∴
∵E、C,F三点共线
∴
∴.
题型五 倍长中线模型
1.(1)解:∵是中线,
∴,
延长到,使,
又,
∴
(2)由(1)可知,,,
在中,,,
∴,即,
∴.
2.(1)解:如图所述,以点为对称中心旋转,得,
∴与关于点成对称中心图形.
(2)解:由(1)可知,与关于点成对称中心图形,
∴,
∴,,
在中,,即,
∴,
∵,
∴,解得,,
∴的长的取值范围.
3.(1)解:由三角形的三边关系可知:,
∵,
∴;
(2)解:延长至E,使,连接,
在中,∵,
∴,
∴,
由三角形的三边关系:,
∴,
∴.
4.(1)解:延长DG至M,使GM=DG,连接MF,
在和中,
∴(SAS),
∴DE=MF=3,
∵DF-MF<DM<DF+MF,
∴7-3<DM<7+3,
即4<DM<10,
∵,
∴4<2DG<10,
∴2<DG<5;
(2)AD=CD+AB,理由如下:
解:延长AE,DC相交于点F,
∵,
∴∠BAE=∠F,
∵点E是BC的中点,
∴BE=CE,
在和中,
∴(AAS),
∴AB=CF,
∵∠BAE=∠F,∠DAF=∠BAE,
∴∠F=∠DAF,
∴AD=FD,
∵FD=CD+CF,CF=AB,
∴AD=CD+AB.
题型六 旋转模型
1.(1)∵∠BAC=90°
∴ ∠EAB+∠DAC=180°-∠BAC=180°-90°=90°
故答案为:90°.
(2)证明:∵ CD⊥MN于D,BE⊥MN于E
∴ ∠ADC=∠BEA=∠BAC=90°
∵ ∠DAC+∠DCA=90°且 ∠DAC+∠EAB=90°
∴ ∠DCA=∠EAB
∵在△DCA和△EAB中
∴△DCA≌△EAB (AAS)
∴ AD=BE且EA=DC
由图可知:DE = EA+AD = DC+BE.
(3)∵ CD⊥MN于D,BE⊥MN于E
∴ ∠ADC=∠BEA=∠BAC=90°
∵ ∠DAC+∠DCA=90°且∠DAC+∠EAB=90°
∴ ∠DCA=∠EAB
∵在△DCA和△EAB中
∴△DCA≌△EAB (AAS)
∴ AD=BE且AE=CD
由图可知:AE = AD +DE
∴ CD= BE + DE.
2.解:(1)结论:.
理由:如图1,将绕点顺时针旋转,使与重合,得到,
则:,,,
∴,即:三点共线,
,
∴,
∴,
,
在和中,
,
,
,
又,
.
(2)结论:.
理由:如图2,将绕点顺时针旋转,使与重合,得到,
则:,
同法(1)可得:,
,
又,
.
3.(1)∵∠CAB=∠EAD
∴∠CAB+∠BAE=∠EAD+∠BAE,
∴ ∠CAE=∠BAD,
∵AB=AC,AE=AD
在△AEC和△ADB中
∴ △AEC≌△ADB(SAS)
(2)CE=BD且CE⊥BD,证明如下:
将直线CE与AB的交点记为点O,
由(1)可知△AEC≌△ADB,
∴ CE=BD, ∠ACE=∠ABD,
∵∠BOF=∠AOC,∠=90°,
∴ ∠BFO=∠CAB=∠=90°,
∴ CE⊥BD.
(3)过A分别做AM⊥CE,AN⊥BD
由(1)知△AEC≌△ADB,
∴两个三角形面积相等
故AM·CE=AN·BD
∴AM=AN
∴AF平分∠DFC
由(2)可知∠BFC=∠BAC=
∴∠DFC=180°-
∴∠CFA=∠DFC=
4.(1)解:,
,
又,,
,
在中,,
故答案为:.
(2)解:如下图所示:过点作的边上的高,过点作的边上的高,由作图及知:
,,,
(同角的余角相等),
在与中有:
(),
,
,,
,,
,
故答案为:.
题型七 垂线模型
1.解:(1)证明:如图1,
∵AD⊥DE,BE⊥DE,
∴∠ADC=∠BEC=90°,
∵∠ACB=90°,
∴∠ACD+∠BCE=90°,∠DAC+∠ACD=90°,
∴∠DAC=∠BCE,
在△ADC和△CEB中,
,
∴△ADC≌△CEB(AAS);
(2)如图2,∵BE⊥EC,AD⊥CE,
∴∠ADC=∠BEC=90°,
∴∠EBC+∠ECB=90°,
∵∠ACB=90°,
∴∠ECB+∠ACE=90°,
∴∠ACD=∠EBC,
在△ADC和△CEB中,
,
∴△ADC≌△CEB(AAS),
∴AD=CE,CD=BE,
∴DE=EC-CD=AD-BE.
(3)DE=BE-AD;
如图3,∵∠ACB=90°,
∴∠ACD+∠BCE=90°
∵AD⊥MN,BE⊥MN,
∴∠ADC=∠CEB=90°,
∴∠ACD+∠DAC=90°,
∴∠DAC=∠ECB,
在△ACD和△CBE中,
,
∴△ACD≌△CBE(AAS),
∴AD=CE,CD=BE,
∴DE=CD-CE=BE-AD.
2.(1)证明:在△ABC和中
,
∴;
∴,
∵,
∴.
(2)解:当时,.理由如下:
∵,
∴,
∵,
∴.
∴.
∴.
3.(1)证明:是等腰直角三角形,
∴,
∵,
∴,
∴,
在△BC与△BDE中,
,
∴
(2)证明:∵,
∴,
∵,
∴,
∴,
∴,
∴.
4.(1)证明:由题意可得,,
∴,,
∵,
∴,
∴,
在和中,
∴
∴,,
∴;
(2),
证明:由题意可得,,
∴,,
∵,
∴,
∴,
在和中,
∴
∴,,
∴;
(3)设,则,
∴
∵,
∴
∴;
(4)如图,过点B作交的延长线于点E,过点F作于点F,
由(1)可得
∴,,
∵,
∴是等腰直角三角形,
∴,
∵面积为18
∴
∴,
∵的长为9,
∴,
∴
题型八 添加条件使三角形全等
1.解:添加的条件为,理由如下:
因为,
所以,
即,
在和中,
,
所以.
2.(1)①③
(2)解:选①时,
在△ABC和中,
,
;
选③时,
在△ABC和中,
,
.
题型九 全等三角形综合问题
1.(1)AD=CB,
理由如下:∵AB∥CD,
∴∠ABD=∠CDB,
同理可得,∠ADB=∠CBD,
在△ABD与△CDB中,
∴△ABD≌△CDB(ASA),
∴AD=CB;
(2)BF=BD,
理由
∵AD=CB,BE=AD,
∴BC=BE,
∵AD∥BC,
∴∠ADB=∠DBF,
∵∠DEF=∠ADC,
∴∠DEF﹣∠DBF=∠ADC﹣∠ADB,
即∠EFB=∠CDB,
在△EFB与△CDB中,
,
∴△EFB≌△CDB(AAS),
∴FB=DB.
2.解:∠B与∠C相等,
理由:∵∠FDC=∠FDE+∠EDC,
又∵∠FDC=∠B+∠BFD,
∴∠FDE+∠EDC=∠B+∠BFD,
又∵∠FDE=∠B,
∴∠BFD=∠EDC,
在△BFD和△CDE中
,
∴△BFD≌△CDE(SAS),
∴∠B=∠C.
3.(1)∵∠A+∠ACD=180°,
∴,
∵,
∴.
(2)∵OE=OF,
∴∠OEF=∠OFE,
∵,
∴∠OEF=∠ODC,∠OFE=∠OCD,
∴∠ODC=∠OCD,
∴OC=OD,
∴OC+OF=OD+OE,
即CF=DE,
在△ECD和△FDC中,
,
∴△ECD≌△FDC(SAS).
4.(1)证明:,
,即,
在和中,
,
;
(2)解:,
,
在和中,
,
,
.
同课章节目录
