第3单元长方体和正方体计算题专项突破(含解析)-2024-2025学年数学五年级下册人教版
文档属性
| 名称 | 第3单元长方体和正方体计算题专项突破(含解析)-2024-2025学年数学五年级下册人教版 |  | |
| 格式 | docx | ||
| 文件大小 | 314.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-15 12:48:17 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第3单元长方体和正方体计算题专项突破-2024-2025学年数学五年级下册人教版
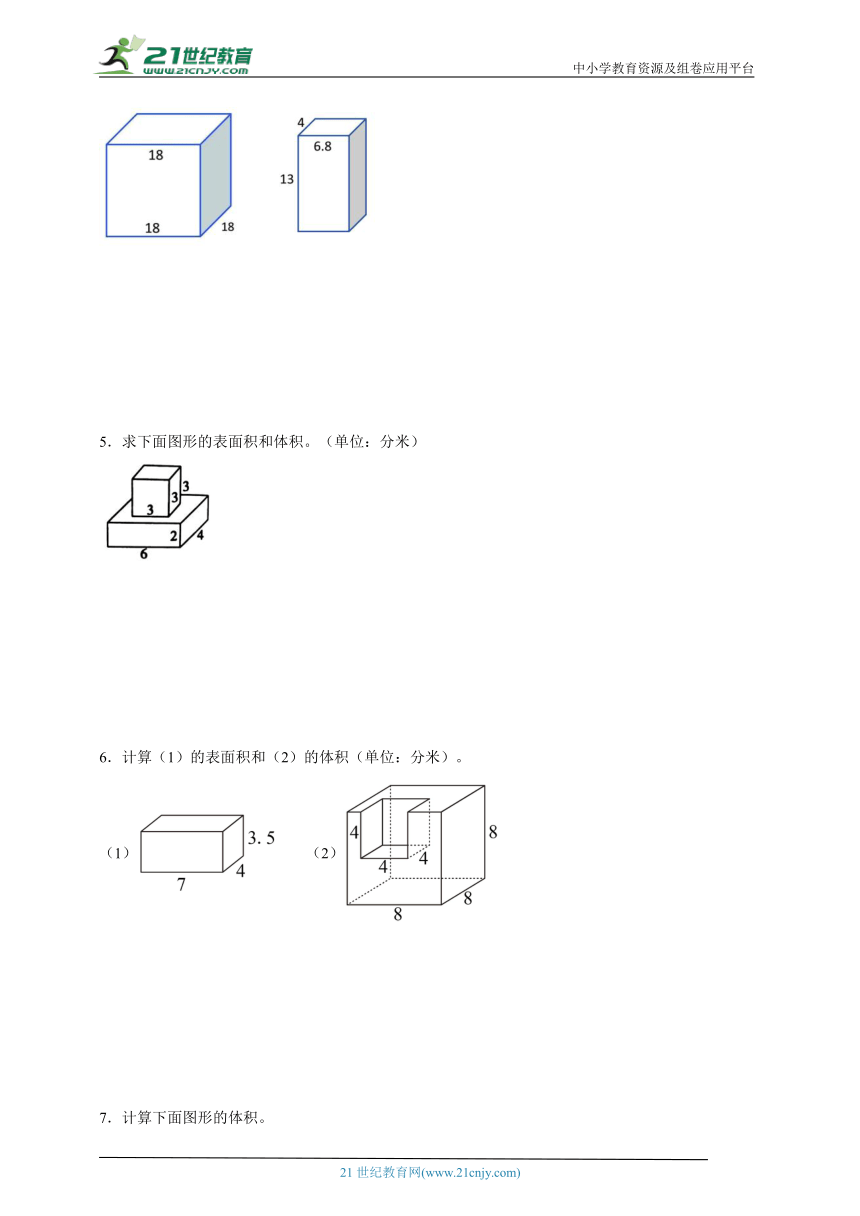
1.计算如图图形的表面积和体积。
2.求出下面图形的表面积和体积。
3.求如图长方体的表面积。(单位:dm)
4.求下面立体图形的表面积和体积。(单位:厘米)
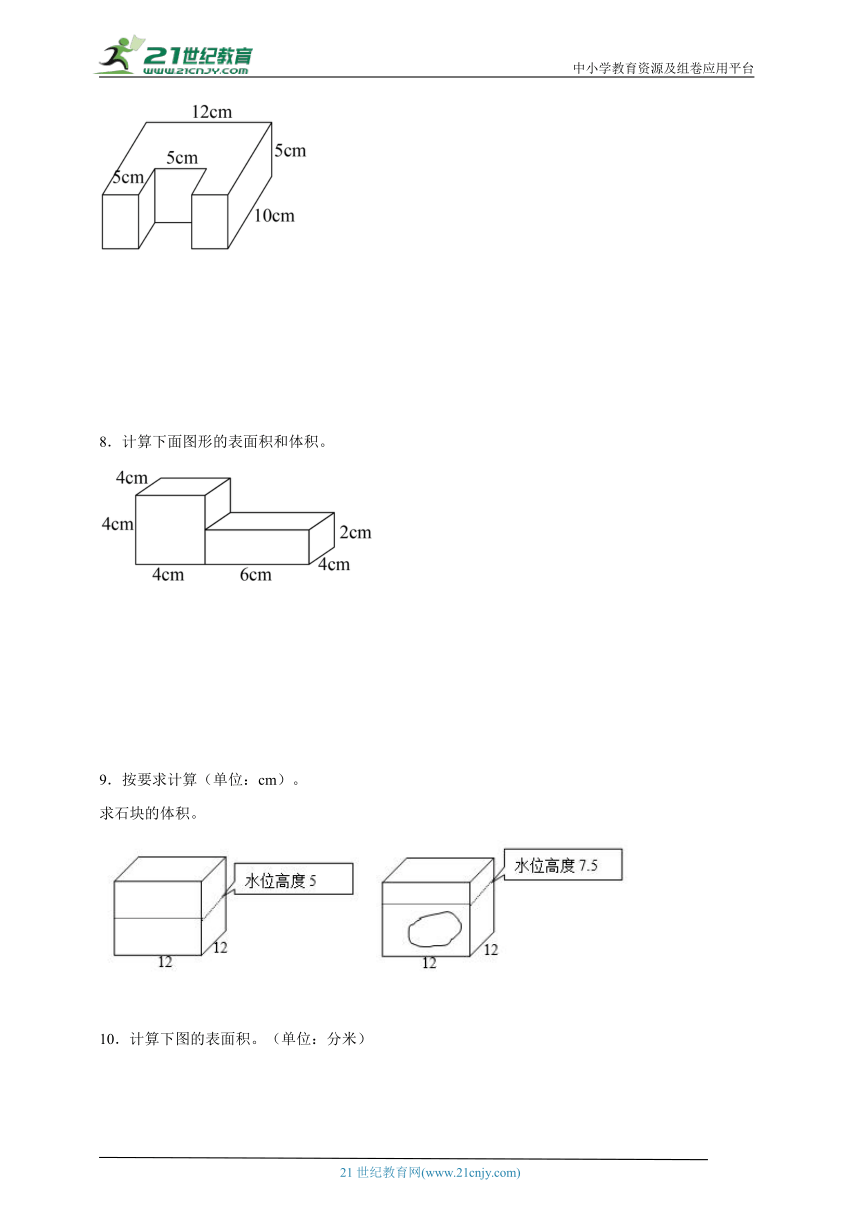
5.求下面图形的表面积和体积。(单位:分米)
6.计算(1)的表面积和(2)的体积(单位:分米)。
(1) (2)
7.计算下面图形的体积。
8.计算下面图形的表面积和体积。
9.按要求计算(单位:cm)。
求石块的体积。
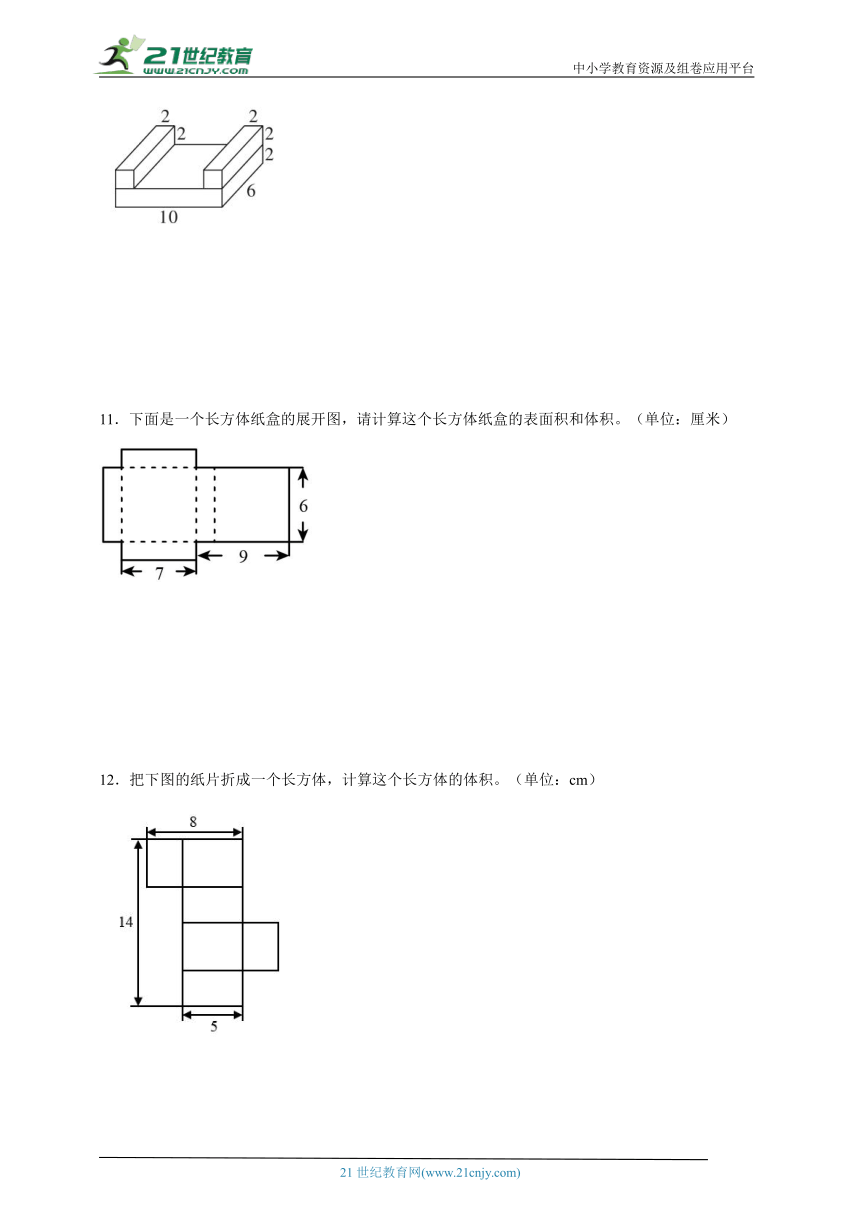
10.计算下图的表面积。(单位:分米)
11.下面是一个长方体纸盒的展开图,请计算这个长方体纸盒的表面积和体积。(单位:厘米)
12.把下图的纸片折成一个长方体,计算这个长方体的体积。(单位:cm)
13.图形计算。
如图:求这个图形的体积?
14.计算下面图形的表面积和体积。(单位:厘米)
15.如图,计算这块空心砖的表面积和体积。(单位:厘米)
16.求下面图形的体积。(单位:厘米)
17.计算下图的表面积和体积。(单位cm)
18.分别计算下面两个图形的表面积和体积。(单位:cm)
《第3单元长方体和正方体计算题专项突破-2024-2025学年数学五年级下册人教版》参考答案
1.486平方厘米;729立方厘米
【分析】根据正方体的表面积公式:S=6a2,正方体的体积公式:V=a3,据此代入数值进行计算即可。
【详解】表面积:9×9×6
=81×6
=486(平方厘米)
9×9×9
=81×9
=729(立方厘米)
2.长方体:表面积128平方厘米;体积96立方厘米
正方体:表面积216平方分米;体积216立方分米
【分析】长方体表面积=(长×宽+长×高+宽×高)×2,长方体体积=长×宽×高,正方体表面积=棱长×棱长×6,正方体体积=棱长×棱长×棱长,据此代入数据解答即可。
【详解】长方体表面积:
(平方厘米)
长方体体积:
(立方厘米)
正方体表面积:
(平方分米)
正方体体积:
(立方分米)
3.
254dm2
【分析】长方体的表面积=(长×宽+长×高+宽×高)×2,据此代入数据计算即可。
【详解】长方体表面积:(9×7+9×4+7×4)×2
=(63+36+28)×2
=127×2
=254(dm2)
4.正方体:1944平方厘米;5832立方厘米;
长方体:335.2平方厘米;353.6立方厘米
【分析】长方体的表面积=(长×宽+长×高+宽×高)×2,长方体的体积=长×宽×高,正方体的表面积=棱长×棱长×6,正方体体积=棱长×棱长×棱长,据此代入数据解答即可。
【详解】正方体表面积:
(平方厘米)
正方体体积:
(立方厘米)
长方体表面积:
(平方厘米)
长方体体积:
(立方厘米)
5.表面积124平方分米;体积75立方分米。
【分析】图形由一个棱长3分米的正方体和一个长6分米、宽4分米、高2分米的长方体叠加而成,图形的表面积是被遮挡了2个正方体的面,即长方体表面积+正方体的4个面面积,长方体表面积=(长×宽+长×高+宽×高)×2,据此计算出图形表面积;图形体积=长方体体积+正方体体积,长方体体积=长×宽×高,正方体体积=棱长×棱长×棱长,据此计算得出答案。
【详解】图形表面积为:
(平方分米)
体积为:
(立方分米)
6.(1)133平方分米;(2)448立方分米
【分析】(1)根据公式:长方体的表面积=(长×宽+长×高+宽×高)×2,代入数据计算即可;
(2)图中这个立体图形的体积等于大正方体的体积减去小正方体的体积。根据公式:正方体的体积=棱长×棱长×棱长,代入数据计算即可。
【详解】(1)
=133(平方分米)
(2)8×8×8-4×4×4
=512-64
=448(立方分米)
7.475cm3
【分析】如下图,把图形的缺口补上,缺口处是一个棱长为5cm的正方体,则图形的体积=长方体的体积-正方体的体积;
根据长方体的体积公式V=abh,正方体的体积公式V=a3,代入数据计算求解。
【详解】12×10×5-5×5×5
=600-125
=475(cm3)
图形的体积是475cm3。
8.168cm2;112cm3
【分析】该立体图形的表面积,就等于一个正方体的表面积加一个长方体的侧面积,根据正方体的表面积=a2×6,长方体的侧面积=(ab+ah)×2,代入数据求表面积即可;
该立体图形的体积,可以看作正方体体积+长方体的体积,左边的正方体棱长为4cm,右边长方体长为6cm,宽为4cm,高为2cm,根据长方体的体积V=abh,正方体的体积V=a3,代入数据求出两个立体图形的体积,再相加即可。
【详解】4×4×6+(6×4+6×2)×2
=16×6+(24+12)×2
=96+36×2
=96+72
=168(cm2)
4×4×4+6×4×2
=16×4+24×2
=64+48
=112(cm3)
图形的表面积是168cm2,体积为112cm3。
9.360cm3
【分析】根据上升部分水的体积等于完全淹没在水面下物体的体积,即石块的体积=上升部分水的体积,根据长方体的体积=长×宽×高,求解即可。
【详解】12×12×(7.5-5)
=12×12×2.5
=144×2.5
=360(cm3)
石块的体积为360cm2。
10.248平方分米
【分析】表面积是指物体外表面积,通常是指物体表面的总面积。上面的两个小长方形和凹进去的长方形合在一起恰好就是一个长方体的表面积。则表面积=长方体的表面积+4个长方形的面积+4个小正方形的面积。长方体的表面积=(长×宽+长×高+宽×高)×2,小长方形的长是6分米,宽是2分米,面积=长×宽。正方形的边长是2分米,面积=边长×边长。
【详解】
=
=
=(平方分米)
(平方分米)
(平方分米)
(平方分米)
则图形的表面积是248平方分米。
11.136平方厘米;84立方厘米
【分析】观察图形可知,这个长方体的长是7厘米,宽是6厘米,高是(9-7)厘米,根据长方体的表面积公式:S=(ab+ah+bh)×2,长方体的体积公式:V=abh,据此进行计算即可。
【详解】9-7=2(厘米)
(7×6+7×2+6×2)×2
=(42+14+12)×2
=68×2
=136(平方厘米)
7×6×2
=42×2
=84(立方厘米)
则这个长方体纸盒的表面积是136平方厘米,体积是84立方厘米。
12.60cm3
【分析】由长方体的展开图可知,该长方体的长为5cm,宽为(8-5=3)cm,高为【(14-3×2)÷2】cm,再根据长方体的体积公式,代入相应数值计算即可解答。
【详解】宽:8-5=3(cm)
高:(14-3×2)÷2
=(14-6)÷2
=8÷2
=4(cm)
5×3×4=60(cm3)
因此这个长方体的体积是60cm3。
13.400立方厘米
【分析】由图意知:长方体的长是24-2-2=20厘米,宽是14-2-2=10厘米,高是2厘米,代谢长方体体积计算公式:长方体体积=长×宽×高。据此解答。
【详解】(24-2×2)×(14-2×2)×2
=20×10×2
=400(立方厘米)
这个图形的体积是400立方厘米。
14.448平方厘米;448立方厘米
【分析】正方体的表面积=棱长×棱长×6,图形的表面积=大正方体的表面积+小正方体四个侧面的面积;正方体的体积=棱长×棱长×棱长,图形的体积=大正方体的体积-小正方体的体积,据此解答。
【详解】8×8×6+4×4×4
=64×6+16×4
=384+64
=448(平方厘米)
8×8×8-4×4×4
=64×8-16×4
=512-64
=448(立方厘米)
所以,图形的表面积是448平方厘米,体积是448立方厘米。
15.表面积:6760平方厘米;体积:27000立方厘米
【分析】大长方体的四个侧面、小长方体的四个侧面,再加上上、下面的面积就是空心砖的表面积;大长方体体积与小长方体体积的差就是空心砖的体积,据此解答。
【详解】40×25×2+30×25×2+12×25×2+10×25×2+40×30×2-12×10×2
=2000+1500+600+500+2400-240
=7000-240
=6760(平方厘米)
40×30×25-12×10×25
=30000-3000
=27000(立方厘米)
16.1250立方厘米
【分析】组合体的体积=大长方体的体积-2个棱长5厘米的正方体体积,长方体体积=长×宽×高,正方体体积=棱长×棱长×棱长,据此列式计算。
【详解】20×5×(10+5)-5×5×5×2
=100×15-250
=1500-250
=1250(立方厘米)
17.392cm2;504cm3
【分析】观察图形可知,该立体图形的表面积等于大正方体的表面积加上小正方体两个面的面积,根据正方体的表面积公式:S=6a2,据此进行计算即可;该立体图形的体积等于大正方体的体积减去小正方体的体积,根据正方体的体积公式:V=a3,据此计算即可。
【详解】8×8×6+2×2×2
=64×6+4×2
=384+8
=392(cm2)
8×8×8-2×2×2
=64×8-4×2
=512-8
=504(cm3)
18.表面积为526,体积为669;表面积为230,体积为165
【分析】看图1可知,一个长方体和正方体叠加之后,减少了两个正方形的表面积,组合图形的表面积等于长方体的表面积加上正方体四个面的表面积,利用表面积公式分别代入计算即可;叠加后体积不变,组合图形的体积等于长方体的体积加上正方体的体积,利用体积公式计算即可。
看图2可知,一个长方体和正方体叠相邻放齐之后,减少了两个长方体侧面的表面积,组合图形的表面积等于正方体的表面积加上长方体上、下、前、后四个面的表面积,表面积公式分别代入计算即可;组合图形的体积等于长方体的体积加上正方体的体积,利用体积公式计算即可。
【详解】图1:
长方体表面积:11×5×4+11×11×2
=55×4+121×2
=220+242
=462()
正方体四个面的表面积:4×4×4
=16×4
=64()
图1的表面积:462+64=526()
长方体体积:11×11×5
=121×5
=605()
正方体体积:4×4×4
=16×4
=64()
图1的体积:605+64=669()
图2:
正方体的表面积:5×5×6
=25×6
=150()
长方体四个面的表面积:10×2×4
=20×4
=80()
图2的表面积:150+80=230()
正方体的体积:5×5×5
=25×5
=125()
长方体的体积:10×2×2
=20×2
=40()
图2的体积:125+40=165()
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第3单元长方体和正方体计算题专项突破-2024-2025学年数学五年级下册人教版
1.计算如图图形的表面积和体积。
2.求出下面图形的表面积和体积。
3.求如图长方体的表面积。(单位:dm)
4.求下面立体图形的表面积和体积。(单位:厘米)
5.求下面图形的表面积和体积。(单位:分米)
6.计算(1)的表面积和(2)的体积(单位:分米)。
(1) (2)
7.计算下面图形的体积。
8.计算下面图形的表面积和体积。
9.按要求计算(单位:cm)。
求石块的体积。
10.计算下图的表面积。(单位:分米)
11.下面是一个长方体纸盒的展开图,请计算这个长方体纸盒的表面积和体积。(单位:厘米)
12.把下图的纸片折成一个长方体,计算这个长方体的体积。(单位:cm)
13.图形计算。
如图:求这个图形的体积?
14.计算下面图形的表面积和体积。(单位:厘米)
15.如图,计算这块空心砖的表面积和体积。(单位:厘米)
16.求下面图形的体积。(单位:厘米)
17.计算下图的表面积和体积。(单位cm)
18.分别计算下面两个图形的表面积和体积。(单位:cm)
《第3单元长方体和正方体计算题专项突破-2024-2025学年数学五年级下册人教版》参考答案
1.486平方厘米;729立方厘米
【分析】根据正方体的表面积公式:S=6a2,正方体的体积公式:V=a3,据此代入数值进行计算即可。
【详解】表面积:9×9×6
=81×6
=486(平方厘米)
9×9×9
=81×9
=729(立方厘米)
2.长方体:表面积128平方厘米;体积96立方厘米
正方体:表面积216平方分米;体积216立方分米
【分析】长方体表面积=(长×宽+长×高+宽×高)×2,长方体体积=长×宽×高,正方体表面积=棱长×棱长×6,正方体体积=棱长×棱长×棱长,据此代入数据解答即可。
【详解】长方体表面积:
(平方厘米)
长方体体积:
(立方厘米)
正方体表面积:
(平方分米)
正方体体积:
(立方分米)
3.
254dm2
【分析】长方体的表面积=(长×宽+长×高+宽×高)×2,据此代入数据计算即可。
【详解】长方体表面积:(9×7+9×4+7×4)×2
=(63+36+28)×2
=127×2
=254(dm2)
4.正方体:1944平方厘米;5832立方厘米;
长方体:335.2平方厘米;353.6立方厘米
【分析】长方体的表面积=(长×宽+长×高+宽×高)×2,长方体的体积=长×宽×高,正方体的表面积=棱长×棱长×6,正方体体积=棱长×棱长×棱长,据此代入数据解答即可。
【详解】正方体表面积:
(平方厘米)
正方体体积:
(立方厘米)
长方体表面积:
(平方厘米)
长方体体积:
(立方厘米)
5.表面积124平方分米;体积75立方分米。
【分析】图形由一个棱长3分米的正方体和一个长6分米、宽4分米、高2分米的长方体叠加而成,图形的表面积是被遮挡了2个正方体的面,即长方体表面积+正方体的4个面面积,长方体表面积=(长×宽+长×高+宽×高)×2,据此计算出图形表面积;图形体积=长方体体积+正方体体积,长方体体积=长×宽×高,正方体体积=棱长×棱长×棱长,据此计算得出答案。
【详解】图形表面积为:
(平方分米)
体积为:
(立方分米)
6.(1)133平方分米;(2)448立方分米
【分析】(1)根据公式:长方体的表面积=(长×宽+长×高+宽×高)×2,代入数据计算即可;
(2)图中这个立体图形的体积等于大正方体的体积减去小正方体的体积。根据公式:正方体的体积=棱长×棱长×棱长,代入数据计算即可。
【详解】(1)
=133(平方分米)
(2)8×8×8-4×4×4
=512-64
=448(立方分米)
7.475cm3
【分析】如下图,把图形的缺口补上,缺口处是一个棱长为5cm的正方体,则图形的体积=长方体的体积-正方体的体积;
根据长方体的体积公式V=abh,正方体的体积公式V=a3,代入数据计算求解。
【详解】12×10×5-5×5×5
=600-125
=475(cm3)
图形的体积是475cm3。
8.168cm2;112cm3
【分析】该立体图形的表面积,就等于一个正方体的表面积加一个长方体的侧面积,根据正方体的表面积=a2×6,长方体的侧面积=(ab+ah)×2,代入数据求表面积即可;
该立体图形的体积,可以看作正方体体积+长方体的体积,左边的正方体棱长为4cm,右边长方体长为6cm,宽为4cm,高为2cm,根据长方体的体积V=abh,正方体的体积V=a3,代入数据求出两个立体图形的体积,再相加即可。
【详解】4×4×6+(6×4+6×2)×2
=16×6+(24+12)×2
=96+36×2
=96+72
=168(cm2)
4×4×4+6×4×2
=16×4+24×2
=64+48
=112(cm3)
图形的表面积是168cm2,体积为112cm3。
9.360cm3
【分析】根据上升部分水的体积等于完全淹没在水面下物体的体积,即石块的体积=上升部分水的体积,根据长方体的体积=长×宽×高,求解即可。
【详解】12×12×(7.5-5)
=12×12×2.5
=144×2.5
=360(cm3)
石块的体积为360cm2。
10.248平方分米
【分析】表面积是指物体外表面积,通常是指物体表面的总面积。上面的两个小长方形和凹进去的长方形合在一起恰好就是一个长方体的表面积。则表面积=长方体的表面积+4个长方形的面积+4个小正方形的面积。长方体的表面积=(长×宽+长×高+宽×高)×2,小长方形的长是6分米,宽是2分米,面积=长×宽。正方形的边长是2分米,面积=边长×边长。
【详解】
=
=
=(平方分米)
(平方分米)
(平方分米)
(平方分米)
则图形的表面积是248平方分米。
11.136平方厘米;84立方厘米
【分析】观察图形可知,这个长方体的长是7厘米,宽是6厘米,高是(9-7)厘米,根据长方体的表面积公式:S=(ab+ah+bh)×2,长方体的体积公式:V=abh,据此进行计算即可。
【详解】9-7=2(厘米)
(7×6+7×2+6×2)×2
=(42+14+12)×2
=68×2
=136(平方厘米)
7×6×2
=42×2
=84(立方厘米)
则这个长方体纸盒的表面积是136平方厘米,体积是84立方厘米。
12.60cm3
【分析】由长方体的展开图可知,该长方体的长为5cm,宽为(8-5=3)cm,高为【(14-3×2)÷2】cm,再根据长方体的体积公式,代入相应数值计算即可解答。
【详解】宽:8-5=3(cm)
高:(14-3×2)÷2
=(14-6)÷2
=8÷2
=4(cm)
5×3×4=60(cm3)
因此这个长方体的体积是60cm3。
13.400立方厘米
【分析】由图意知:长方体的长是24-2-2=20厘米,宽是14-2-2=10厘米,高是2厘米,代谢长方体体积计算公式:长方体体积=长×宽×高。据此解答。
【详解】(24-2×2)×(14-2×2)×2
=20×10×2
=400(立方厘米)
这个图形的体积是400立方厘米。
14.448平方厘米;448立方厘米
【分析】正方体的表面积=棱长×棱长×6,图形的表面积=大正方体的表面积+小正方体四个侧面的面积;正方体的体积=棱长×棱长×棱长,图形的体积=大正方体的体积-小正方体的体积,据此解答。
【详解】8×8×6+4×4×4
=64×6+16×4
=384+64
=448(平方厘米)
8×8×8-4×4×4
=64×8-16×4
=512-64
=448(立方厘米)
所以,图形的表面积是448平方厘米,体积是448立方厘米。
15.表面积:6760平方厘米;体积:27000立方厘米
【分析】大长方体的四个侧面、小长方体的四个侧面,再加上上、下面的面积就是空心砖的表面积;大长方体体积与小长方体体积的差就是空心砖的体积,据此解答。
【详解】40×25×2+30×25×2+12×25×2+10×25×2+40×30×2-12×10×2
=2000+1500+600+500+2400-240
=7000-240
=6760(平方厘米)
40×30×25-12×10×25
=30000-3000
=27000(立方厘米)
16.1250立方厘米
【分析】组合体的体积=大长方体的体积-2个棱长5厘米的正方体体积,长方体体积=长×宽×高,正方体体积=棱长×棱长×棱长,据此列式计算。
【详解】20×5×(10+5)-5×5×5×2
=100×15-250
=1500-250
=1250(立方厘米)
17.392cm2;504cm3
【分析】观察图形可知,该立体图形的表面积等于大正方体的表面积加上小正方体两个面的面积,根据正方体的表面积公式:S=6a2,据此进行计算即可;该立体图形的体积等于大正方体的体积减去小正方体的体积,根据正方体的体积公式:V=a3,据此计算即可。
【详解】8×8×6+2×2×2
=64×6+4×2
=384+8
=392(cm2)
8×8×8-2×2×2
=64×8-4×2
=512-8
=504(cm3)
18.表面积为526,体积为669;表面积为230,体积为165
【分析】看图1可知,一个长方体和正方体叠加之后,减少了两个正方形的表面积,组合图形的表面积等于长方体的表面积加上正方体四个面的表面积,利用表面积公式分别代入计算即可;叠加后体积不变,组合图形的体积等于长方体的体积加上正方体的体积,利用体积公式计算即可。
看图2可知,一个长方体和正方体叠相邻放齐之后,减少了两个长方体侧面的表面积,组合图形的表面积等于正方体的表面积加上长方体上、下、前、后四个面的表面积,表面积公式分别代入计算即可;组合图形的体积等于长方体的体积加上正方体的体积,利用体积公式计算即可。
【详解】图1:
长方体表面积:11×5×4+11×11×2
=55×4+121×2
=220+242
=462()
正方体四个面的表面积:4×4×4
=16×4
=64()
图1的表面积:462+64=526()
长方体体积:11×11×5
=121×5
=605()
正方体体积:4×4×4
=16×4
=64()
图1的体积:605+64=669()
图2:
正方体的表面积:5×5×6
=25×6
=150()
长方体四个面的表面积:10×2×4
=20×4
=80()
图2的表面积:150+80=230()
正方体的体积:5×5×5
=25×5
=125()
长方体的体积:10×2×2
=20×2
=40()
图2的体积:125+40=165()
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
