人教版数学第26-29章巩固练习卷(含解析)-2024-2025学年数学九年级下册人教版
文档属性
| 名称 | 人教版数学第26-29章巩固练习卷(含解析)-2024-2025学年数学九年级下册人教版 |

|
|
| 格式 | docx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-16 00:00:00 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第26-29章巩固练习卷-2024-2025学年数学九年级下册人教版
一、单选题
1.如图所示是年六盘水市马拉松领奖台示意图,则此领奖台的俯视图是( )
A. B. C. D.
2.反比例函数图象经过点,则的值是( )
A.12 B. C. D.
3.中,,,下列结论:①;②;③,其中结论正确的个数为( )
A.0 B.1 C.2 D.3
4.如图,四边形是平行四边形,点B在x轴上,的延长线与y轴交于点D,反比例函数的图象经过点,且与边交于点E.若,且,则点E的纵坐标为( )
A. B. C. D.
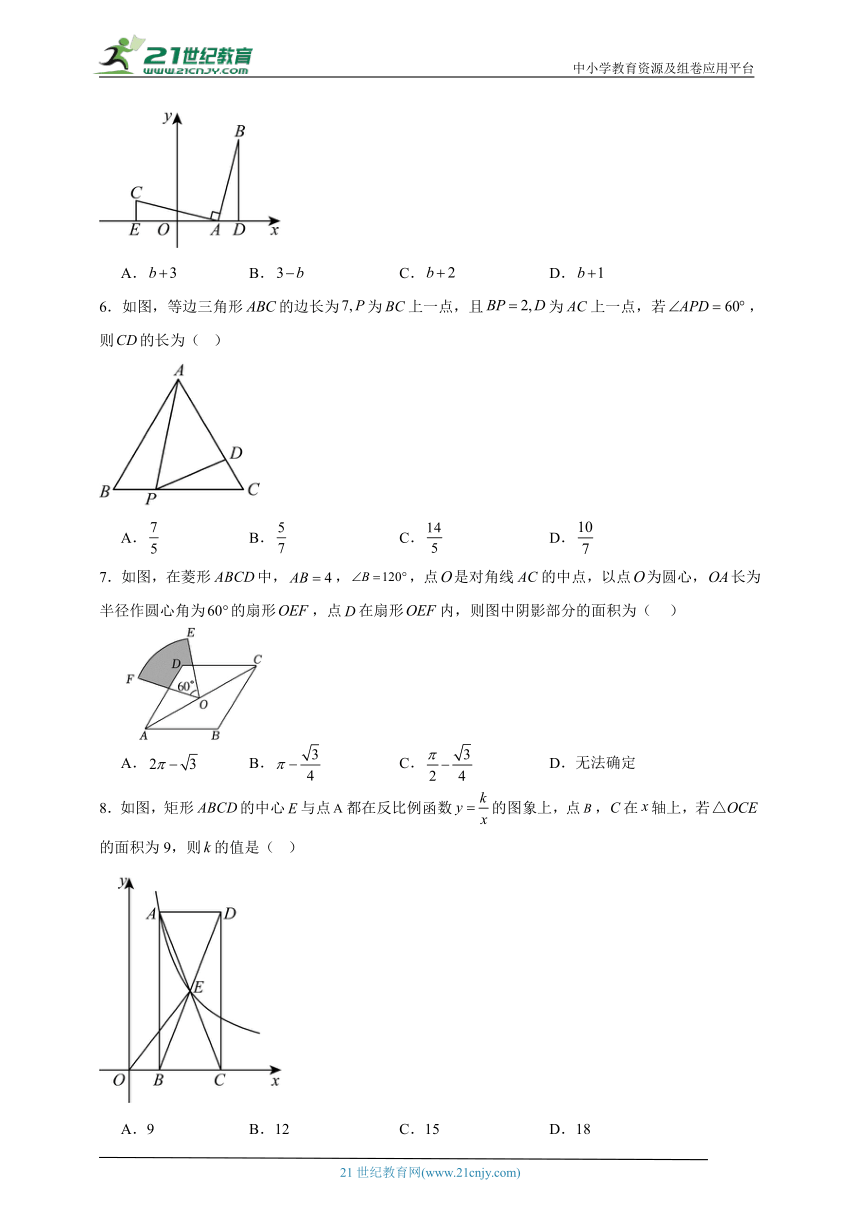
5.如图,在平面直角坐标系中,点,,,且,若轴于点D,轴于点E,则长为( )
A. B. C. D.
6.如图,等边三角形的边长为为上一点,且为上一点,若,则的长为( )
A. B. C. D.
7.如图,在菱形中,,,点是对角线的中点,以点为圆心,长为半径作圆心角为的扇形,点在扇形内,则图中阴影部分的面积为( )
A. B. C. D.无法确定
8.如图,矩形的中心与点都在反比例函数的图象上,点,在轴上,若的面积为9,则的值是( )
A.9 B.12 C.15 D.18
二、填空题
9.已知点是反比例函数图象上的两点,则 .(填“>”,“=”或“<”)
10.成语“立竿见影”在《辞源》里的解释为“竿立而影现,喻收效迅速.”希望小组开展了运用阳光下的影长测量学校内旗杆高度的实践活动.小组内同学进行了如下操作:如图,同一时刻在阳光照射下,旗杆的影长,小明的影长,已知小明的身高,则旗杆的高为 .
11.如图,在平面直角坐标系中,点为反比例函数的图象上一点,轴于点,点为轴负半轴上一点,且,连接、,若的面积为9,则的值为 .
12.在综合实践课上,孔明同学设计了如图测量河塘宽的方案:在河塘外选一点,连接,,测得,,延长,分别到,两点,使,,有测得,则河塘宽 .
13.如图,在中,,分别与相交于点D、E,若,则 .
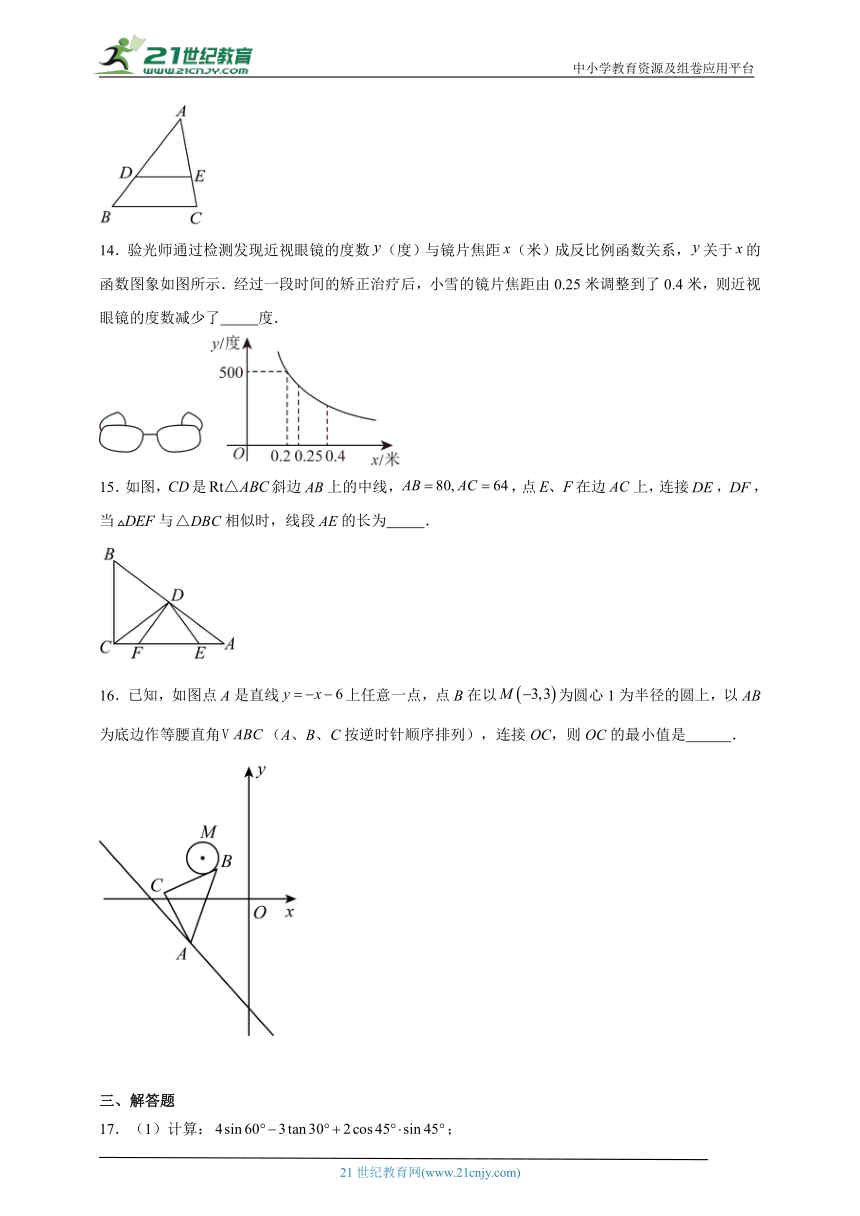
14.验光师通过检测发现近视眼镜的度数(度)与镜片焦距(米)成反比例函数关系,关于的函数图象如图所示.经过一段时间的矫正治疗后,小雪的镜片焦距由0.25米调整到了0.4米,则近视眼镜的度数减少了 度.
15.如图,是斜边上的中线,,点在边上,连接,,当与相似时,线段的长为 .
16.已知,如图点A是直线上任意一点,点B在以为圆心1为半径的圆上,以AB为底边作等腰直角(A、B、C按逆时针顺序排列),连接OC,则OC的最小值是 .
三、解答题
17.(1)计算:;
(2)在中,,求的正弦值、余弦值和正切值.
18.实验数据显示,一般成人喝50毫升某品牌白酒后开始计时,血液中酒精含量y(毫克/百毫升)与时间x(时)变化的图象如图(图象由线段与部分双曲线组成)所示.国家规定,车辆驾驶人员血液中的酒精含大于或等于20(毫克/百毫升)时属于“酒后驾驶”,不能驾车上路.
(1)求部分双曲线的函数表达式,并写出相应的自变量的取值范围;
(2)参照上述数学模型,假设某驾驶员晚上在家喝完50毫升该品牌白酒,第二天早上能否驾去上班?请说明理由.
19.如图,在中,点在边上,平分,分别交于点.
(1)求证:;
(2)求证:.
20.如图,的顶点.若向右平移4个单位长度,再向下平移3个单位长度得到,且点C的对应点坐标是.
(1)画出,并直接写出点的坐标;
(2)若内有一点经过以上平移后的对应点为,直接写出点的坐标;
(3)求的面积.
21.等边中,点分别是边上的点(不与端点重合),连接相交于点,且.
(1)如图,求的度数;
(2)如图,点分别是线段上的动点,连接相交于点,平分,平分,求证:;
(3)将绕点逆时针旋转得到,连接,在线段上存在一点,当的值最小时,连接交于点,求的值.
22.如图,一款可调节的笔记本电脑支架放置在水平桌面上,通过调节与的仰角与的大小来达成个人舒适的高度,已知调节杆,,的最大仰角为.
(1)当点离桌面高度大约时,手腕最舒适,请问应该调整哪个角的大小?调整为多少度?
(2)在(1)的条件下,求点到桌面的最大高度.(参考数据:)
23.如图,在平面直角坐标系中,正比例函数的图象与反比例函数()的图象相交于、两点,轴于点,点的坐标为,连接、.
(1)求该反比例函数的表达式;
(2)在该反比例函数的图象上是否存在点,使得的面积与的面积相等?若存在,请求出点的坐标;若不存在,请说明理由.
24.在平面直角坐标系中,直线:与反比例函数的图象相交于,两点,与轴正半轴相交于点,与轴正半轴相交于点,连接.
(1)求和的值;
(2)如图,当点在点的左侧时,过点作轴的平行线,过点作轴的平行线,两线相交于点,连接,求证:把分成面积相等的两部分;
(3)“三等分角”是数学史上一个著名问题.今天人们已经知道,仅用圆规和直尺是不可能作出的.在研究这个问题的过程中,数学家帕普斯借助反比例函数给出了一种“三等分锐角”的方法:在()中,将直线绕点旋转,当线段满足某一等量关系时,即可使得.设为反比例函数的图象上的点,连接,若,请求出点的坐标.(小贴士:)
《第26-29章巩固练习卷-2024-2025学年数学九年级下册人教版》参考答案
题号 1 2 3 4 5 6 7 8
答案 B A B A D D A B
1.B
【分析】本题主要考查简单组合体的三视图,解题的关键是掌握三视图的画法.根据俯视图的画法即可解决,注意看得见的轮廓线用实线,看不见的轮廓线用虚线.
【详解】
解:由题意可得此领奖台的俯视图是,
故选:B.
2.A
【分析】本题考查了反比例函数图象上点的坐标特点:点在反比例函数图象上,则点的坐标满足反比例函数解析式;把点的坐标代入中,即可求得的值.
【详解】解:∵反比例函数图象经过点,
∴,
∴;
故选:A.
3.B
【分析】本题考查锐角三角函数的定义即:在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.设,则,根据勾股定理求出,再根据锐角三角函数的定义解答.
【详解】解:在中,,,
设,则,
∴,
①,②;③.
故选:B.
4.A
【分析】由题意可得,再根据四边形是平行四边形求得,然后根据可得,即;进一步得到反比例函数为、直线解析式为,再将代入求得满足题意的x,然后将代入即可得出答案.
【详解】解:∵,,
∴,
∵四边形是平行四边形
∴
∴,
∵
∴,即,
∴,
∴反比例函数为,
设直线解析式为,
把,代入可得:
,解得:,
∴直线解析式为,
将代入可得:,解得:,
∵点E在第一象限,
∴,
把代入,
解得:,
则点E的纵坐标为∶
故选∶A.
【点睛】本题主要考查了一次函数和反比例函数的综合、平行四边形的性质等知识点,正确求得反比例函数和直线解析式是解答本题的关键.
5.D
【分析】本题考查了全等三角形的判定与性质以及平面直角坐标系的相关知识,解题的关键是通过证明三角形全等得到对应边相等来求解的长度.
先证明,再根据全等三角形对应边相等求出与,与的关系,最后通过线段的加减求出的长度.
【详解】已知,
则.
轴,轴,
.
又,
,且,
,
在和中,,
.
,
,
,
故选:D.
6.D
【分析】本题主要考查相似三角形的判定与性质,等边三角形的性质,解答本题的关键是熟练掌握相似三角形的性质.由等边三角形的性质结合条件可证明,由相似三角形的性质可求得.
【详解】解:等边三角形的边长为7,
,,
,
,
又,且,
,
,
,即,
,
故选:D.
7.A
【分析】如图,连接,在上取点,使,连接.证明,推出,利用即可求解.
【详解】解:如图,连接,在上取点,使,连接.
在菱形中,,点O是对角线的中点,,
,,
,
∴是等边三角形,
,
,
∵
∴,
,
,
∴,
∴,
.
,
,,
.
故选:A.
【点睛】本题考查了菱形的性质,三角形全等的判定与性质,解直角三角形,扇形的面积,作出辅助线,构造三角形全等,利用是解题的关键.
8.B
【分析】本题考查矩形的性质,三角形中位线的性质,待定系数法求解析式.
过点E作于点F,由矩形的性质与三角形中位线的性质得到,设点A的坐标为,点E的坐标为,则,得到.根据,推出,即可解答.
【详解】解:过点E作于点F,
∵在矩形中,,,,
∴,
∴,
∵,
∴,
设点A的坐标为,点E的坐标为,
∵点,在反比例函数的图象上,
∴,
∴,
∵,,
∴,,,
∴,
∴,
∵,
即,
∴,
∴,
∴.
故选:B.
9.
【分析】本题主要考查反比例函数图象上点的坐标特征.先根据反比例函数的解析式判断出函数图象所在的象限及其增减性,再根据各点横坐标的值判断出各点所在的象限,进而可得出结论.
【详解】解:反比例函数中,,
∴函数图象的两个分支分别位于第一、三象限,且在每一象限内y随x的增大而减小.
∵,
∴点A在第三象限、B在第一象限,
∴,
故答案为:.
10.
【分析】本题考查了相似三角形的应用和平行投影,解题的关键是根据相似三角形的性质得到同一时刻同一地点物体的高度与其影长的比相等.
设该旗杆的高度为,根据三角形相似的性质得到同一时刻同一地点物体的高度与其影长的比相等,即有,然后解方程即可.
【详解】解:设该旗杆的高度为,
根据题意,得,
解得:.
即该旗杆的高度是 .
故答案为:.
11.6
【分析】本题考查了反比例函数图象上点的坐标特征、反比例函数k值的几何意义,设B点坐标为,则C点坐标为,,再根据反比例函数图象上点的坐标特征求出k值即可.
【详解】解:设B点坐标为,则C点坐标为,则,
∵,
∴
∴,
∴,
∴解得,
故答案为:6.
12.
【分析】本题考查了相似三角形的判定与性质的应用;由题意得,由相似三角形的性质即可求解.
【详解】解:∵,
即,且,
∴,
∴,
∴
即河塘宽;
故答案为:.
13.5
【分析】本题考查相似三角形的判定与性质.根据题意可以得到和相似,由相似三角形的面积比等于相似比的平方,可以求得的面积,从而可求得四边形的面积.
【详解】解:∵,
∴,
∵
∴,
∴,
∴,
∴,
故答案为:5.
14.
【分析】本题考查待定系数法求反比例函数解析式,以及反比例函数的实际应用,读懂题意,掌握课本知识是解决问题的关键.由已知设,则有图象知点满足解析式,代入求,则解析式为:,令,时,分别求的值后作差即可.
【详解】解:设,
把代入,
,
函数解析式为,
当时,,
当时,,
度数减少了(度,
故答案为:.
15.或
【分析】根据是斜边的中线得到,进而得到,根据与相似, 得到或,所以分三种情况讨论:①②③,分别求解即可.
【详解】解:是斜边的中线,,
,
∴,
当时,
∴,则,
∵在中,,
,
,则,
,
,
∴,
当或时,
,又,
,
,
,
,
,
,
,
∴
综上所述,的长为或
故答案为:或.
【点睛】本题考查了相似三角形的判定与性质,等腰三角形的判定,勾股定理,全等三角形的判定和性质,三角函数的应用,解题的关键是分情况讨论相等的角.
16.
【分析】本题主要考查了相似三角形的判定与性质、旋转的性质、一次函数与几何的综合、等腰三角形的判定与性质等知识点,正确作出辅助线、构造相似三角形成为解题的关键.
如图:顺时针旋转得到,的对应点为,连接,则,;根据等腰直角三角形的性质推得得到,只需求出的最小值;如图:当共线且垂直于直线时,取最小值;然后说明点,运用两点间距离公式得到,进而得到的最小值为,最后代入即可解答.
【详解】解:如图:顺时针旋转得到,的对应点为,连接,则,,
∴,
∵以AB为底边作等腰直角,
∴,,
∴
∴,即,
∴
∴,
∴即,
要求的最小值,直接求得的最小值即可,
如图:当共线且垂直于直线时,取最小值,
设直线与y轴的交点为E,过A作轴与D,
当时,,即,
∴,
∵直线与y轴正方向的夹角为,
∴是等腰直角三角形,
∴,
∵轴,
∴,即,
∴,
∴,即的最小值为.
∴OC的最小值为.
故答案为:.
17.(1);(2)
【分析】本题主要考查了特殊角三角函数值的混合计算,解直角三角形,勾股定理,熟知特殊角三角函数值和三角函数的定义是解题的关键.
(1)先计算特殊角三角函数值,再根据二次根式的计算法则求解即可;
(2)先利用勾股定理求出的长,再根据正弦,余弦和正切的定义求解即可.
【详解】解:(1)
(2)在中,由勾股定理,得
∴.
18.(1)
(2)第二天早上能驾车去上班,见解析
【分析】本题为一次函数和反比例函数的应用,涉及待定系数法等知识点.掌握自变量、函数值等知识是解题的关键.
(1)首先求得线段所在直线的解析式,然后求得点A的坐标,代入反比例函数的解析式即可求解;
(2)把代入反比例函数解析式可求得时间,结合规定可进行判断.
【详解】(1)解:设直线的解析式为,
直线过,
,
,
直线的解析式为,
当时,,即,
设双曲线的解析式为,
将点代入得:,
;
(2)解:由得,
当时,,
从晚上到第二天早上时间间距为10小时,
,
第二天早上能驾车去上班.
19.(1)见解析
(2)见解析
【分析】本题考查相似三角形的判定和性质,等腰三角形的判定和性质:
(1)角平分线得到,三角形的内角和定理,得到,进而得到即可;
(2)根据,得到,,推出,证明,得到,进而得到即可得出结论.
【详解】(1)证明:∵平分,
∴,
设,,
∴,,
∴,
又∵,
∴;
(2)∵,
∴,,
∵,
∴,
∴,
∵,,
∴,
∴,
∴.
20.(1)见解析,
(2)
(3)
【分析】1)根据平移规律,确定变换后的坐标,画图即可.
(2)根据平移规律,确定变换后的坐标即可.
(3)利用分割求面积,解答即可.
本题考查了坐标的平移,分割法计算面积,熟练掌握相应的知识是解题的关键.
【详解】(1)解:根据题意,得.向右平移4个单位长度,再向下平移3个单位长度得到新坐标为,画图如下:
.
则即为所求,且.
(2)解:根据题意,点经过以上平移后的对应点为,且.
(3)解:由,
故的面积为:.
21.(1)
(2)证明见解析
(3)
【分析】()由等边三角形的性质得,,进而得,得到,再根据三角形外角性质即可求解;
()作的平分线,交于,可得出,从而,,进而证得,从而得,同理可得,进而即可求证;
()由题意可知是内一点,要求,则考查费马点知识,由等边三角形费马点在重心可确定点的位置,进而利用特殊直角三角形设参求解即可.
【详解】(1)解∵是等边三角形,
∴,,
∵,
∴,
∴,
∵是的外角,
∴;
(2)证明:如图,作的平分线,
∵,
∴,
∵平分,平分,
∴,,
∴,,
∴,
又∵平分,
∴,
∵,
∴,
∴,
同理可得,,
∴,
∴,
∵,
∴,
又∵,
∴,
∴,
即;
(3)解:将顺时针旋转得到,将顺时针旋转得到,连接、,
由旋转得,,,
∴,是等边三角形,
∴,,
∴,
∴,
即当共线时,的值最小,如图,
连接,则是等边三角形,
∴,
∵是等边三角形,
∴,
∴垂直平分,
∴,
∵是等边三角形,
∴,
∴,
∴垂直平分,
即是三条高线的交点,
∴,
设,则,
在中,,
∴,
∵,
∴,
∵,,
∴,
∴,,
过作交的延长线于点,
∵,
∴,,
∴,
在中,,
∵,,
∴,
∴,
∴,
∴
解得,
∴.
【点睛】本题考查了全等三角形的判定和性质,等边三角形的判定和性质,直角三角形的性质,旋转的性质,相似三角形的判定和性质,勾股定理,三角形的重心等,解决问题的关键是作出辅助线,构造全等三角形.
22.(1)调整,使得
(2)
【分析】本题主要考查了解直角三角形的应用,解题的关键是熟练掌握三角函数的定义.
(1)过点B作于点F,求出,根据,即可得出;
(2)过点A作于点G,则,根据,的最大仰角为求出的最大值,即可得出答案.
【详解】(1)解:过点B作于点F,如图所示:
则,
∵,,
∴,
∵,
∴应该调整,使得.
(2)解:如图,过点A作于点G,则,
∵,的最大仰角为
∴的最大值为:,
∴点到桌面的最大高度为.
23.(1)
(2)存在,点的坐标为或
【分析】本题考查了反比例函数的图象与性质,正比例函数的图象与性质,三角形的面积,解题的关键是掌握相关知识.
(1)由轴于点,得到的横坐标为,将其代入正比例函数中,求出,再将代入反比例函数中,求出,即可求解;
(2)联立正比例函数与反比例函数,求出,,结合,,得到,,进而得出,,根据“的面积与的面积相等”列方程求出,即可求解.
【详解】(1)解:轴于点,
的横坐标为,
在正比例函数中,令,则,
,
将代入反比例函数中,得:,
反比例函数的表达式为;
(2)存在,
联立,
解得:或,
,,
,,
,,
,,
的面积与的面积相等,
,
解得:或,
在反比例函数的图象上存在点,使得的面积与的面积相等,点的坐标为或.
24.(1),
(2)证明见解析
(3)或
【分析】()利用待定系数法解答即可;
()求出直线和直线的交点横坐标,再求出的中点坐标即可求证;
()由题意得,设,可得,,即得,进而可得,过作轴,再利用三角函数解得即可求解;
本题考查了待定系数法求反比例函数解析式,反比例函数的几何应用,三角函数,掌握反比例函数的图象和性质是解题的关键.
【详解】(1)解:将代入得,,
,
将点代入反比例函数中,得,
∴;
(2)证明:由()知,
反比例函数表达式为,
令,
整理得,,
解得,,
,
,
设直线表达式为,则,
解得,
直线表达式为,
联立直线和直线得,,
,
解得,
,,
的中点横坐标为,
和交点为中点,
把分成面积相等的两部分;
(3)解:如图,中,,,
,
设,则,,
,
,
,
,
,
,
如图,过作轴,则,
设,
,,
,
,
,
,
;
同理可得;
综上,点的坐标为或.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第26-29章巩固练习卷-2024-2025学年数学九年级下册人教版
一、单选题
1.如图所示是年六盘水市马拉松领奖台示意图,则此领奖台的俯视图是( )
A. B. C. D.
2.反比例函数图象经过点,则的值是( )
A.12 B. C. D.
3.中,,,下列结论:①;②;③,其中结论正确的个数为( )
A.0 B.1 C.2 D.3
4.如图,四边形是平行四边形,点B在x轴上,的延长线与y轴交于点D,反比例函数的图象经过点,且与边交于点E.若,且,则点E的纵坐标为( )
A. B. C. D.
5.如图,在平面直角坐标系中,点,,,且,若轴于点D,轴于点E,则长为( )
A. B. C. D.
6.如图,等边三角形的边长为为上一点,且为上一点,若,则的长为( )
A. B. C. D.
7.如图,在菱形中,,,点是对角线的中点,以点为圆心,长为半径作圆心角为的扇形,点在扇形内,则图中阴影部分的面积为( )
A. B. C. D.无法确定
8.如图,矩形的中心与点都在反比例函数的图象上,点,在轴上,若的面积为9,则的值是( )
A.9 B.12 C.15 D.18
二、填空题
9.已知点是反比例函数图象上的两点,则 .(填“>”,“=”或“<”)
10.成语“立竿见影”在《辞源》里的解释为“竿立而影现,喻收效迅速.”希望小组开展了运用阳光下的影长测量学校内旗杆高度的实践活动.小组内同学进行了如下操作:如图,同一时刻在阳光照射下,旗杆的影长,小明的影长,已知小明的身高,则旗杆的高为 .
11.如图,在平面直角坐标系中,点为反比例函数的图象上一点,轴于点,点为轴负半轴上一点,且,连接、,若的面积为9,则的值为 .
12.在综合实践课上,孔明同学设计了如图测量河塘宽的方案:在河塘外选一点,连接,,测得,,延长,分别到,两点,使,,有测得,则河塘宽 .
13.如图,在中,,分别与相交于点D、E,若,则 .
14.验光师通过检测发现近视眼镜的度数(度)与镜片焦距(米)成反比例函数关系,关于的函数图象如图所示.经过一段时间的矫正治疗后,小雪的镜片焦距由0.25米调整到了0.4米,则近视眼镜的度数减少了 度.
15.如图,是斜边上的中线,,点在边上,连接,,当与相似时,线段的长为 .
16.已知,如图点A是直线上任意一点,点B在以为圆心1为半径的圆上,以AB为底边作等腰直角(A、B、C按逆时针顺序排列),连接OC,则OC的最小值是 .
三、解答题
17.(1)计算:;
(2)在中,,求的正弦值、余弦值和正切值.
18.实验数据显示,一般成人喝50毫升某品牌白酒后开始计时,血液中酒精含量y(毫克/百毫升)与时间x(时)变化的图象如图(图象由线段与部分双曲线组成)所示.国家规定,车辆驾驶人员血液中的酒精含大于或等于20(毫克/百毫升)时属于“酒后驾驶”,不能驾车上路.
(1)求部分双曲线的函数表达式,并写出相应的自变量的取值范围;
(2)参照上述数学模型,假设某驾驶员晚上在家喝完50毫升该品牌白酒,第二天早上能否驾去上班?请说明理由.
19.如图,在中,点在边上,平分,分别交于点.
(1)求证:;
(2)求证:.
20.如图,的顶点.若向右平移4个单位长度,再向下平移3个单位长度得到,且点C的对应点坐标是.
(1)画出,并直接写出点的坐标;
(2)若内有一点经过以上平移后的对应点为,直接写出点的坐标;
(3)求的面积.
21.等边中,点分别是边上的点(不与端点重合),连接相交于点,且.
(1)如图,求的度数;
(2)如图,点分别是线段上的动点,连接相交于点,平分,平分,求证:;
(3)将绕点逆时针旋转得到,连接,在线段上存在一点,当的值最小时,连接交于点,求的值.
22.如图,一款可调节的笔记本电脑支架放置在水平桌面上,通过调节与的仰角与的大小来达成个人舒适的高度,已知调节杆,,的最大仰角为.
(1)当点离桌面高度大约时,手腕最舒适,请问应该调整哪个角的大小?调整为多少度?
(2)在(1)的条件下,求点到桌面的最大高度.(参考数据:)
23.如图,在平面直角坐标系中,正比例函数的图象与反比例函数()的图象相交于、两点,轴于点,点的坐标为,连接、.
(1)求该反比例函数的表达式;
(2)在该反比例函数的图象上是否存在点,使得的面积与的面积相等?若存在,请求出点的坐标;若不存在,请说明理由.
24.在平面直角坐标系中,直线:与反比例函数的图象相交于,两点,与轴正半轴相交于点,与轴正半轴相交于点,连接.
(1)求和的值;
(2)如图,当点在点的左侧时,过点作轴的平行线,过点作轴的平行线,两线相交于点,连接,求证:把分成面积相等的两部分;
(3)“三等分角”是数学史上一个著名问题.今天人们已经知道,仅用圆规和直尺是不可能作出的.在研究这个问题的过程中,数学家帕普斯借助反比例函数给出了一种“三等分锐角”的方法:在()中,将直线绕点旋转,当线段满足某一等量关系时,即可使得.设为反比例函数的图象上的点,连接,若,请求出点的坐标.(小贴士:)
《第26-29章巩固练习卷-2024-2025学年数学九年级下册人教版》参考答案
题号 1 2 3 4 5 6 7 8
答案 B A B A D D A B
1.B
【分析】本题主要考查简单组合体的三视图,解题的关键是掌握三视图的画法.根据俯视图的画法即可解决,注意看得见的轮廓线用实线,看不见的轮廓线用虚线.
【详解】
解:由题意可得此领奖台的俯视图是,
故选:B.
2.A
【分析】本题考查了反比例函数图象上点的坐标特点:点在反比例函数图象上,则点的坐标满足反比例函数解析式;把点的坐标代入中,即可求得的值.
【详解】解:∵反比例函数图象经过点,
∴,
∴;
故选:A.
3.B
【分析】本题考查锐角三角函数的定义即:在直角三角形中,锐角的正弦为对边比斜边,余弦为邻边比斜边,正切为对边比邻边.设,则,根据勾股定理求出,再根据锐角三角函数的定义解答.
【详解】解:在中,,,
设,则,
∴,
①,②;③.
故选:B.
4.A
【分析】由题意可得,再根据四边形是平行四边形求得,然后根据可得,即;进一步得到反比例函数为、直线解析式为,再将代入求得满足题意的x,然后将代入即可得出答案.
【详解】解:∵,,
∴,
∵四边形是平行四边形
∴
∴,
∵
∴,即,
∴,
∴反比例函数为,
设直线解析式为,
把,代入可得:
,解得:,
∴直线解析式为,
将代入可得:,解得:,
∵点E在第一象限,
∴,
把代入,
解得:,
则点E的纵坐标为∶
故选∶A.
【点睛】本题主要考查了一次函数和反比例函数的综合、平行四边形的性质等知识点,正确求得反比例函数和直线解析式是解答本题的关键.
5.D
【分析】本题考查了全等三角形的判定与性质以及平面直角坐标系的相关知识,解题的关键是通过证明三角形全等得到对应边相等来求解的长度.
先证明,再根据全等三角形对应边相等求出与,与的关系,最后通过线段的加减求出的长度.
【详解】已知,
则.
轴,轴,
.
又,
,且,
,
在和中,,
.
,
,
,
故选:D.
6.D
【分析】本题主要考查相似三角形的判定与性质,等边三角形的性质,解答本题的关键是熟练掌握相似三角形的性质.由等边三角形的性质结合条件可证明,由相似三角形的性质可求得.
【详解】解:等边三角形的边长为7,
,,
,
,
又,且,
,
,
,即,
,
故选:D.
7.A
【分析】如图,连接,在上取点,使,连接.证明,推出,利用即可求解.
【详解】解:如图,连接,在上取点,使,连接.
在菱形中,,点O是对角线的中点,,
,,
,
∴是等边三角形,
,
,
∵
∴,
,
,
∴,
∴,
.
,
,,
.
故选:A.
【点睛】本题考查了菱形的性质,三角形全等的判定与性质,解直角三角形,扇形的面积,作出辅助线,构造三角形全等,利用是解题的关键.
8.B
【分析】本题考查矩形的性质,三角形中位线的性质,待定系数法求解析式.
过点E作于点F,由矩形的性质与三角形中位线的性质得到,设点A的坐标为,点E的坐标为,则,得到.根据,推出,即可解答.
【详解】解:过点E作于点F,
∵在矩形中,,,,
∴,
∴,
∵,
∴,
设点A的坐标为,点E的坐标为,
∵点,在反比例函数的图象上,
∴,
∴,
∵,,
∴,,,
∴,
∴,
∵,
即,
∴,
∴,
∴.
故选:B.
9.
【分析】本题主要考查反比例函数图象上点的坐标特征.先根据反比例函数的解析式判断出函数图象所在的象限及其增减性,再根据各点横坐标的值判断出各点所在的象限,进而可得出结论.
【详解】解:反比例函数中,,
∴函数图象的两个分支分别位于第一、三象限,且在每一象限内y随x的增大而减小.
∵,
∴点A在第三象限、B在第一象限,
∴,
故答案为:.
10.
【分析】本题考查了相似三角形的应用和平行投影,解题的关键是根据相似三角形的性质得到同一时刻同一地点物体的高度与其影长的比相等.
设该旗杆的高度为,根据三角形相似的性质得到同一时刻同一地点物体的高度与其影长的比相等,即有,然后解方程即可.
【详解】解:设该旗杆的高度为,
根据题意,得,
解得:.
即该旗杆的高度是 .
故答案为:.
11.6
【分析】本题考查了反比例函数图象上点的坐标特征、反比例函数k值的几何意义,设B点坐标为,则C点坐标为,,再根据反比例函数图象上点的坐标特征求出k值即可.
【详解】解:设B点坐标为,则C点坐标为,则,
∵,
∴
∴,
∴,
∴解得,
故答案为:6.
12.
【分析】本题考查了相似三角形的判定与性质的应用;由题意得,由相似三角形的性质即可求解.
【详解】解:∵,
即,且,
∴,
∴,
∴
即河塘宽;
故答案为:.
13.5
【分析】本题考查相似三角形的判定与性质.根据题意可以得到和相似,由相似三角形的面积比等于相似比的平方,可以求得的面积,从而可求得四边形的面积.
【详解】解:∵,
∴,
∵
∴,
∴,
∴,
∴,
故答案为:5.
14.
【分析】本题考查待定系数法求反比例函数解析式,以及反比例函数的实际应用,读懂题意,掌握课本知识是解决问题的关键.由已知设,则有图象知点满足解析式,代入求,则解析式为:,令,时,分别求的值后作差即可.
【详解】解:设,
把代入,
,
函数解析式为,
当时,,
当时,,
度数减少了(度,
故答案为:.
15.或
【分析】根据是斜边的中线得到,进而得到,根据与相似, 得到或,所以分三种情况讨论:①②③,分别求解即可.
【详解】解:是斜边的中线,,
,
∴,
当时,
∴,则,
∵在中,,
,
,则,
,
,
∴,
当或时,
,又,
,
,
,
,
,
,
,
∴
综上所述,的长为或
故答案为:或.
【点睛】本题考查了相似三角形的判定与性质,等腰三角形的判定,勾股定理,全等三角形的判定和性质,三角函数的应用,解题的关键是分情况讨论相等的角.
16.
【分析】本题主要考查了相似三角形的判定与性质、旋转的性质、一次函数与几何的综合、等腰三角形的判定与性质等知识点,正确作出辅助线、构造相似三角形成为解题的关键.
如图:顺时针旋转得到,的对应点为,连接,则,;根据等腰直角三角形的性质推得得到,只需求出的最小值;如图:当共线且垂直于直线时,取最小值;然后说明点,运用两点间距离公式得到,进而得到的最小值为,最后代入即可解答.
【详解】解:如图:顺时针旋转得到,的对应点为,连接,则,,
∴,
∵以AB为底边作等腰直角,
∴,,
∴
∴,即,
∴
∴,
∴即,
要求的最小值,直接求得的最小值即可,
如图:当共线且垂直于直线时,取最小值,
设直线与y轴的交点为E,过A作轴与D,
当时,,即,
∴,
∵直线与y轴正方向的夹角为,
∴是等腰直角三角形,
∴,
∵轴,
∴,即,
∴,
∴,即的最小值为.
∴OC的最小值为.
故答案为:.
17.(1);(2)
【分析】本题主要考查了特殊角三角函数值的混合计算,解直角三角形,勾股定理,熟知特殊角三角函数值和三角函数的定义是解题的关键.
(1)先计算特殊角三角函数值,再根据二次根式的计算法则求解即可;
(2)先利用勾股定理求出的长,再根据正弦,余弦和正切的定义求解即可.
【详解】解:(1)
(2)在中,由勾股定理,得
∴.
18.(1)
(2)第二天早上能驾车去上班,见解析
【分析】本题为一次函数和反比例函数的应用,涉及待定系数法等知识点.掌握自变量、函数值等知识是解题的关键.
(1)首先求得线段所在直线的解析式,然后求得点A的坐标,代入反比例函数的解析式即可求解;
(2)把代入反比例函数解析式可求得时间,结合规定可进行判断.
【详解】(1)解:设直线的解析式为,
直线过,
,
,
直线的解析式为,
当时,,即,
设双曲线的解析式为,
将点代入得:,
;
(2)解:由得,
当时,,
从晚上到第二天早上时间间距为10小时,
,
第二天早上能驾车去上班.
19.(1)见解析
(2)见解析
【分析】本题考查相似三角形的判定和性质,等腰三角形的判定和性质:
(1)角平分线得到,三角形的内角和定理,得到,进而得到即可;
(2)根据,得到,,推出,证明,得到,进而得到即可得出结论.
【详解】(1)证明:∵平分,
∴,
设,,
∴,,
∴,
又∵,
∴;
(2)∵,
∴,,
∵,
∴,
∴,
∵,,
∴,
∴,
∴.
20.(1)见解析,
(2)
(3)
【分析】1)根据平移规律,确定变换后的坐标,画图即可.
(2)根据平移规律,确定变换后的坐标即可.
(3)利用分割求面积,解答即可.
本题考查了坐标的平移,分割法计算面积,熟练掌握相应的知识是解题的关键.
【详解】(1)解:根据题意,得.向右平移4个单位长度,再向下平移3个单位长度得到新坐标为,画图如下:
.
则即为所求,且.
(2)解:根据题意,点经过以上平移后的对应点为,且.
(3)解:由,
故的面积为:.
21.(1)
(2)证明见解析
(3)
【分析】()由等边三角形的性质得,,进而得,得到,再根据三角形外角性质即可求解;
()作的平分线,交于,可得出,从而,,进而证得,从而得,同理可得,进而即可求证;
()由题意可知是内一点,要求,则考查费马点知识,由等边三角形费马点在重心可确定点的位置,进而利用特殊直角三角形设参求解即可.
【详解】(1)解∵是等边三角形,
∴,,
∵,
∴,
∴,
∵是的外角,
∴;
(2)证明:如图,作的平分线,
∵,
∴,
∵平分,平分,
∴,,
∴,,
∴,
又∵平分,
∴,
∵,
∴,
∴,
同理可得,,
∴,
∴,
∵,
∴,
又∵,
∴,
∴,
即;
(3)解:将顺时针旋转得到,将顺时针旋转得到,连接、,
由旋转得,,,
∴,是等边三角形,
∴,,
∴,
∴,
即当共线时,的值最小,如图,
连接,则是等边三角形,
∴,
∵是等边三角形,
∴,
∴垂直平分,
∴,
∵是等边三角形,
∴,
∴,
∴垂直平分,
即是三条高线的交点,
∴,
设,则,
在中,,
∴,
∵,
∴,
∵,,
∴,
∴,,
过作交的延长线于点,
∵,
∴,,
∴,
在中,,
∵,,
∴,
∴,
∴,
∴
解得,
∴.
【点睛】本题考查了全等三角形的判定和性质,等边三角形的判定和性质,直角三角形的性质,旋转的性质,相似三角形的判定和性质,勾股定理,三角形的重心等,解决问题的关键是作出辅助线,构造全等三角形.
22.(1)调整,使得
(2)
【分析】本题主要考查了解直角三角形的应用,解题的关键是熟练掌握三角函数的定义.
(1)过点B作于点F,求出,根据,即可得出;
(2)过点A作于点G,则,根据,的最大仰角为求出的最大值,即可得出答案.
【详解】(1)解:过点B作于点F,如图所示:
则,
∵,,
∴,
∵,
∴应该调整,使得.
(2)解:如图,过点A作于点G,则,
∵,的最大仰角为
∴的最大值为:,
∴点到桌面的最大高度为.
23.(1)
(2)存在,点的坐标为或
【分析】本题考查了反比例函数的图象与性质,正比例函数的图象与性质,三角形的面积,解题的关键是掌握相关知识.
(1)由轴于点,得到的横坐标为,将其代入正比例函数中,求出,再将代入反比例函数中,求出,即可求解;
(2)联立正比例函数与反比例函数,求出,,结合,,得到,,进而得出,,根据“的面积与的面积相等”列方程求出,即可求解.
【详解】(1)解:轴于点,
的横坐标为,
在正比例函数中,令,则,
,
将代入反比例函数中,得:,
反比例函数的表达式为;
(2)存在,
联立,
解得:或,
,,
,,
,,
,,
的面积与的面积相等,
,
解得:或,
在反比例函数的图象上存在点,使得的面积与的面积相等,点的坐标为或.
24.(1),
(2)证明见解析
(3)或
【分析】()利用待定系数法解答即可;
()求出直线和直线的交点横坐标,再求出的中点坐标即可求证;
()由题意得,设,可得,,即得,进而可得,过作轴,再利用三角函数解得即可求解;
本题考查了待定系数法求反比例函数解析式,反比例函数的几何应用,三角函数,掌握反比例函数的图象和性质是解题的关键.
【详解】(1)解:将代入得,,
,
将点代入反比例函数中,得,
∴;
(2)证明:由()知,
反比例函数表达式为,
令,
整理得,,
解得,,
,
,
设直线表达式为,则,
解得,
直线表达式为,
联立直线和直线得,,
,
解得,
,,
的中点横坐标为,
和交点为中点,
把分成面积相等的两部分;
(3)解:如图,中,,,
,
设,则,,
,
,
,
,
,
,
如图,过作轴,则,
设,
,,
,
,
,
,
;
同理可得;
综上,点的坐标为或.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
