2024-2025学年安徽省合肥市第九中学高二下学期第一次教学质量检测数学试卷(含答案)
文档属性
| 名称 | 2024-2025学年安徽省合肥市第九中学高二下学期第一次教学质量检测数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 230.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-15 18:35:37 | ||
图片预览



文档简介
2024-2025学年安徽省合肥市第九中学高二下学期第一次教学质量检测数学试卷
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.曲线在点处的切线方程为( )
A. B. C. D.
2.同室人各写一张贺年卡,先集中起来,然后每人从中拿一张别人送出的贺年卡,则张贺年卡不同的分配方式有( )
A. 种 B. 种 C. 种 D. 种
3.不等式的解集为( )
A. B.
C. D.
4.函数的部分图象大致为( )
A. B.
C. D.
5.已知函数在区间上单调递增,则的最小值为 .
A. B. C. D.
6.上午要上语文、数学、体育和外语四门功课,而数学老师因故不能上第二节和第四节,则不同排课方案的种数是( )
A. B. C. D.
7.设是上的可导函数,分别为的导函数,且,则当时,有( )
A. B.
C. D.
8.若都有成立,则的最大值为( )
A. B. C. D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.下列说法正确的是( )
A.
B. 设函数的导函数为,且,则
C. 函数的单调递减区间为
D. 函数有两个极值点
10.定义在上的函数的导函数的图象如图所示,则下列结论正确的是( )
A. 函数在上单调递减 B. 函数在上单调递减
C. 函数在处取得极小值 D. 函数在处取得极大值
11.若函数既有极大值也有极小值,则 .
A. B. C. D.
三、填空题:本题共3小题,每小题5分,共15分。
12.哪吒天登顶中国影史票房榜,之后持续狂飙,上映天票房突破亿;天登顶全球动画电影票房榜,电影中哪吒需要从风、火、水、雷、土五种灵珠中选出四个,按顺序排列成法阵对抗敌人,已知风灵珠和火灵珠不能相邻,问共有多少种法阵组合方式 用数字作答
13.已知函数,若在上恒成立,则实数的取值范围是 .
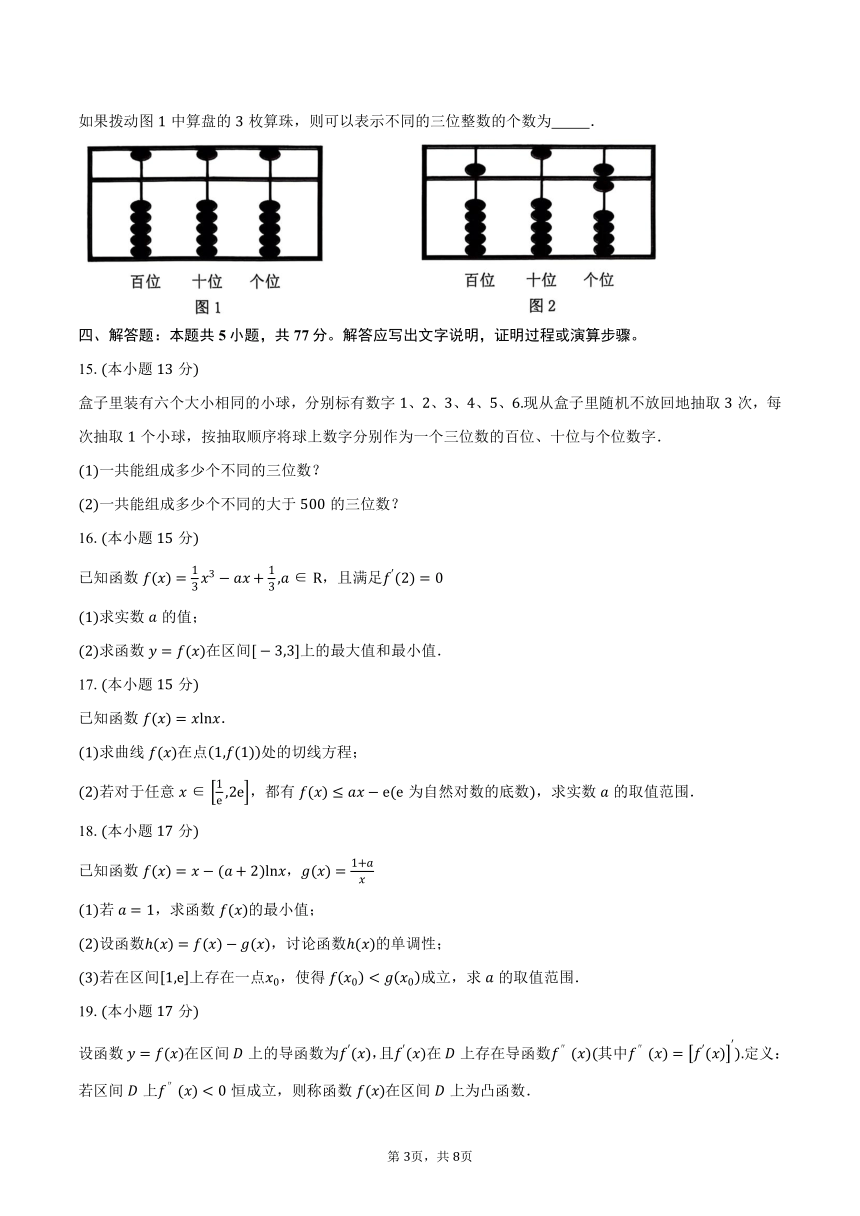
14.程大位是明代珠算发明家,徽州人他所编撰的直指算法统宗是最早记载珠算开平方、开立方方法的古算书之一,它完成了计算由筹算向珠算的转变,使算盘成为主要的计算工具算盘其形长方,周为木框,内贯直柱,俗称“档”现有一种算盘如图共三档,自右向左分别表示个位、十位和百位,档中横以梁,梁上一珠,下拨一珠记作数字:梁下五珠,上拨一珠记作数字例如:图中算盘表示整数如果拨动图中算盘的枚算珠,则可以表示不同的三位整数的个数为 .
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
盒子里装有六个大小相同的小球,分别标有数字、、、、、现从盒子里随机不放回地抽取次,每次抽取个小球,按抽取顺序将球上数字分别作为一个三位数的百位、十位与个位数字.
一共能组成多少个不同的三位数?
一共能组成多少个不同的大于的三位数?
16.本小题分
已知函数,且满足
求实数的值;
求函数在区间上的最大值和最小值.
17.本小题分
已知函数.
求曲线在点处的切线方程;
若对于任意,都有为自然对数的底数,求实数的取值范围.
18.本小题分
已知函数,
若,求函数的最小值;
设函数,讨论函数的单调性;
若在区间上存在一点,使得成立,求的取值范围.
19.本小题分
设函数在区间上的导函数为,且在上存在导函数其中定义:若区间上恒成立,则称函数在区间上为凸函数.
若函数,判断在区间上是否为凸函数,说明理由;
若函数.
(ⅰ)若在上为“凸函数”,求的取值范围;
(ⅱ)若,判断在区间上的零点个数.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.解:因为抽取的三位数各不同,所以组成三位数的总数为.
解:百位为或,则个位、十位是剩余个数字中的两个,
则有个大于的三位数.
16.解:因为,
所以,
令,即方程,
解得
由知,,所以,
令,即,
解得.
列表如下:
当时,单调递增:
当时,单调递减:
当时,单调递增.
所以有极大值;有极小值
又.
所以函数在区间上的最大值为,最小值为.
17.解:由,得,
又,,所以在点处的切线方程为.
由题可知,,
所以,设,,
则,令,解得,
当时,,所以在单调递减,
当时,,所以在单调递增,
又,即,所以.
18.解:当时,,其中,则,
由可得,由可得,
所以,函数的减区间为,增区间为,
所以,.
因为,其中,
则,
当时,即当时,由可得,由可得,
此时,函数的减区间为,增区间为;
当时,即当时,
由可得,由可得或,
此时,函数的增区间为、,减区间为;
当时,即当时,对任意的,,
此时,函数的增区间为,无减区间;
当时,即当时,
由可得或,由可得,
此时,函数的增区间为、,减区间为.
综上所述,当时,函数的减区间为,增区间为;
当时,函数的增区间为、,减区间为;
当时,函数的增区间为,无减区间;
当时,函数的增区间为、,减区间为.
由可知,当时,函数在上单调递增,则,不合乎题意;
当时,函数在上单调递减,在上单调递增,
若,则时,则函数在上单调递减,在上单调递增,
所以,,
设,其中,则,
所以,函数在上单调递减,则,合乎题意;
若,即当时,函数在上单调递减,
所以,,解得,
因为,则.
综上所述,实数的取值范围是.
19.解:,,
,因为,,
在区间上为凸函数.
由可得其定义域为,且,
所以,
若在上为“凸函数”可得在恒成立,
当时,显然符合题意;
当时,需满足,可得,
综上可得的取值范围为;
(ⅱ)若,可得,所以,
令,则;
易知在区间上恒成立,
因此可得在上单调递减;
显然,
根据零点存在定理可得存在使得,
当时,,即在上为单调递减,
当时,,即在上为单调递增;
又,显然在上不存在零点;
而,结合单调性可得在上存在一个零点;
综上可知,在区间上仅有个零点.
第1页,共1页
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.曲线在点处的切线方程为( )
A. B. C. D.
2.同室人各写一张贺年卡,先集中起来,然后每人从中拿一张别人送出的贺年卡,则张贺年卡不同的分配方式有( )
A. 种 B. 种 C. 种 D. 种
3.不等式的解集为( )
A. B.
C. D.
4.函数的部分图象大致为( )
A. B.
C. D.
5.已知函数在区间上单调递增,则的最小值为 .
A. B. C. D.
6.上午要上语文、数学、体育和外语四门功课,而数学老师因故不能上第二节和第四节,则不同排课方案的种数是( )
A. B. C. D.
7.设是上的可导函数,分别为的导函数,且,则当时,有( )
A. B.
C. D.
8.若都有成立,则的最大值为( )
A. B. C. D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.下列说法正确的是( )
A.
B. 设函数的导函数为,且,则
C. 函数的单调递减区间为
D. 函数有两个极值点
10.定义在上的函数的导函数的图象如图所示,则下列结论正确的是( )
A. 函数在上单调递减 B. 函数在上单调递减
C. 函数在处取得极小值 D. 函数在处取得极大值
11.若函数既有极大值也有极小值,则 .
A. B. C. D.
三、填空题:本题共3小题,每小题5分,共15分。
12.哪吒天登顶中国影史票房榜,之后持续狂飙,上映天票房突破亿;天登顶全球动画电影票房榜,电影中哪吒需要从风、火、水、雷、土五种灵珠中选出四个,按顺序排列成法阵对抗敌人,已知风灵珠和火灵珠不能相邻,问共有多少种法阵组合方式 用数字作答
13.已知函数,若在上恒成立,则实数的取值范围是 .
14.程大位是明代珠算发明家,徽州人他所编撰的直指算法统宗是最早记载珠算开平方、开立方方法的古算书之一,它完成了计算由筹算向珠算的转变,使算盘成为主要的计算工具算盘其形长方,周为木框,内贯直柱,俗称“档”现有一种算盘如图共三档,自右向左分别表示个位、十位和百位,档中横以梁,梁上一珠,下拨一珠记作数字:梁下五珠,上拨一珠记作数字例如:图中算盘表示整数如果拨动图中算盘的枚算珠,则可以表示不同的三位整数的个数为 .
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
盒子里装有六个大小相同的小球,分别标有数字、、、、、现从盒子里随机不放回地抽取次,每次抽取个小球,按抽取顺序将球上数字分别作为一个三位数的百位、十位与个位数字.
一共能组成多少个不同的三位数?
一共能组成多少个不同的大于的三位数?
16.本小题分
已知函数,且满足
求实数的值;
求函数在区间上的最大值和最小值.
17.本小题分
已知函数.
求曲线在点处的切线方程;
若对于任意,都有为自然对数的底数,求实数的取值范围.
18.本小题分
已知函数,
若,求函数的最小值;
设函数,讨论函数的单调性;
若在区间上存在一点,使得成立,求的取值范围.
19.本小题分
设函数在区间上的导函数为,且在上存在导函数其中定义:若区间上恒成立,则称函数在区间上为凸函数.
若函数,判断在区间上是否为凸函数,说明理由;
若函数.
(ⅰ)若在上为“凸函数”,求的取值范围;
(ⅱ)若,判断在区间上的零点个数.
参考答案
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.解:因为抽取的三位数各不同,所以组成三位数的总数为.
解:百位为或,则个位、十位是剩余个数字中的两个,
则有个大于的三位数.
16.解:因为,
所以,
令,即方程,
解得
由知,,所以,
令,即,
解得.
列表如下:
当时,单调递增:
当时,单调递减:
当时,单调递增.
所以有极大值;有极小值
又.
所以函数在区间上的最大值为,最小值为.
17.解:由,得,
又,,所以在点处的切线方程为.
由题可知,,
所以,设,,
则,令,解得,
当时,,所以在单调递减,
当时,,所以在单调递增,
又,即,所以.
18.解:当时,,其中,则,
由可得,由可得,
所以,函数的减区间为,增区间为,
所以,.
因为,其中,
则,
当时,即当时,由可得,由可得,
此时,函数的减区间为,增区间为;
当时,即当时,
由可得,由可得或,
此时,函数的增区间为、,减区间为;
当时,即当时,对任意的,,
此时,函数的增区间为,无减区间;
当时,即当时,
由可得或,由可得,
此时,函数的增区间为、,减区间为.
综上所述,当时,函数的减区间为,增区间为;
当时,函数的增区间为、,减区间为;
当时,函数的增区间为,无减区间;
当时,函数的增区间为、,减区间为.
由可知,当时,函数在上单调递增,则,不合乎题意;
当时,函数在上单调递减,在上单调递增,
若,则时,则函数在上单调递减,在上单调递增,
所以,,
设,其中,则,
所以,函数在上单调递减,则,合乎题意;
若,即当时,函数在上单调递减,
所以,,解得,
因为,则.
综上所述,实数的取值范围是.
19.解:,,
,因为,,
在区间上为凸函数.
由可得其定义域为,且,
所以,
若在上为“凸函数”可得在恒成立,
当时,显然符合题意;
当时,需满足,可得,
综上可得的取值范围为;
(ⅱ)若,可得,所以,
令,则;
易知在区间上恒成立,
因此可得在上单调递减;
显然,
根据零点存在定理可得存在使得,
当时,,即在上为单调递减,
当时,,即在上为单调递增;
又,显然在上不存在零点;
而,结合单调性可得在上存在一个零点;
综上可知,在区间上仅有个零点.
第1页,共1页
同课章节目录
