湘教版(2024)九年级下册数学 4.2.2.1 用列表法求概率 课件(共30张PPT)
文档属性
| 名称 | 湘教版(2024)九年级下册数学 4.2.2.1 用列表法求概率 课件(共30张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 16.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-15 17:43:49 | ||
图片预览











文档简介
(共30张PPT)
第四章 投影与视图 4.2.2
概率及其计算
湘教版(2024)九年级下册数学课件
4.2.2.1 用列表法求概率
01
新课导入
03
课堂练习
02
新课讲解
04
课堂小结
目录
新课导入
第一部分
PART 01
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
活动1:一枚硬币连续掷两次,求下列事件概率.
(1)两次全部正面朝上;
(2)两次全部反面朝上;
(3)一次正面朝上,一次反面朝上.
思考:解决上述问题,能否用一个表格先列举出所有可能结果,再解题呢?
新课导入
正 反
正 正正 正反
反 反正 反反
第二次
第一次
活动1:一枚硬币连续掷两次,求下列事件概率.
(1)两次全部正面朝上;
(2)两次全部反面朝上;
(3)一次正面朝上,一次反面朝上.
若能先列出表格,列举出试验的所有结果,再求确定事件的概率,是否要简捷一些.
新课导入
新课讲解
第二部分
PART 02
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
李明和刘英各掷一枚骰子,如果两枚骰子的点数之和为奇数,则李明赢;如果两枚骰子的点数之和为偶数,刘英赢. 这个游戏对双方公平吗?
新课讲解
游戏双方公平是指双发获胜的可能性相等,各掷一枚骰子,可能出现的结果数目较多,为不重不漏地列出所有可能的结果,通常采用列表法.
新课讲解
从表中可以看出,所有可能结果共有36个. 由于骰子是均匀的,这些结果出现的可能性相等.
新课讲解
满足两枚骰子的点数为偶数的可能结果有18个(表中的蓝色),两枚骰子的点数为奇数的可能结果有18个(表中的红色). 因此,
P(点数之和为偶数) .
P(点数之和为奇数) .
由此可见,这个游戏对双方而言是公平的.
新课讲解
如图,袋中装有大小和质地都相同的4个球:2红2白. 从中依次任意取出2个球(第1次取出的球不放回袋中), 求下列事件的概率:
A:取出的2个球同色;
B:取出2个白球.
新课讲解
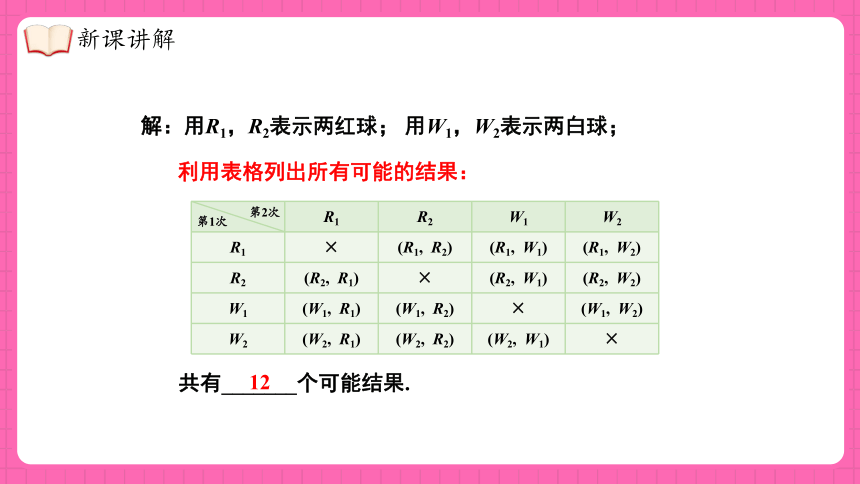
解:用R1,R2表示两红球; 用W1,W2表示两白球;
利用表格列出所有可能的结果:
R1 R2 W1 W2
R1 × (R1, R2) (R1, W1) (R1, W2)
R2 (R2, R1) × (R2, W1) (R2, W2)
W1 (W1, R1) (W1, R2) × (W1, W2)
W2 (W2, R1) (W2, R2) (W2, W1) ×
第1次
第2次
共有_______个可能结果.
12
新课讲解
A:取出的2个球同色
______________________________________(共____种);
B:取出的2个白球
______________________________________(共____种);
(R1, R2)
(R2, R1)
(W1, W2)
(W2, W1)
4
(W1, W2)
(W2, W1)
2
新课讲解
如图,袋中装有大小和质地都相同的4个球:2红2白. 从中依次任意取出2个球(第1次取出的球不放回袋中), 求下列事件的概率:
A:取出的2个球同色;
B:取出2个白球.
新课讲解
如图,袋中装有大小和质地都相同的4个球:2红2白. 从中依次任意取出2个球(第1次取出的球放回袋中), 求下列事件的概率:
A:取出的2个球同色;
B:取出2个白球.
新课讲解
解:用R1,R2表示两红球; 用W1,W2表示两白球;
利用表格列出所有可能的结果:
R1 R2 W1 W2
R1 (R1, R1) (R1, R2) (R1, W1) (R1, W2)
R2 (R2, R1) (R2, R2) (R2, W1) (R2, W2)
W1 (W1, R1) (W1, R2) (W1, W1) (W1, W2)
W2 (W2, R1) (W2, R2) (W2, W1) (W2, W2)
第1次
第2次
新课讲解
试验出现各种结果的个数是有限个.
用列表法求概率适用的对象是:
试验涉及两个因素或分两步完成,如掷两个骰子,抽两张卡片,两次摸球等.
当试验为摸球或抽卡片时,一定要分清第一次摸球或抽卡片后,“球”与“卡”是否放回,即“放回”与“不放回”结果是不同的.
归纳小结
1.如图,有三条绳子穿过一块木板,姐妹两人分别站在木板的左、右两边,各选该边的一段绳子.若每边每段绳子被选中的机会相等, 则两人选到同一条绳子的概率为多少?
新课讲解
解:用A1,A2,A3示三条绳子,
利用表格列出所有可能的结果:
A1 A2 A3
A1 (A1, A1) (A1, A2) (A1, A3)
A2 (A2, A1) (A2, A2) (A2, A3)
A3 (A3, A1) (A3, A2) (A3, A3)
姐姐
妹妹
共有9个可能结果,其中两人选到同一条绳子的情况有3种,
新课讲解
2.小军同时抛掷两枚骰子,求两枚骰子点数之和小于7的概率.
解:利用表格列出所有可能的结果:
新课讲解
共有36个可能结果,其中两枚骰子点数之和小于7的结果有15种,
新课讲解
课堂练习
第三部分
PART 03
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
1.从1,2,3,4,5五个数中任意取出2个数做加法,其和为偶数的概率是( )
A. B. C. D.
C
课堂练习
2.均匀的正四面体的各面上依次标有1,2,3,4四个数字,同时抛掷两个这样的正四面体,着地的一面数字之和为5的概率是( )
A. B. C. D.
B
课堂练习
3.从1,2,﹣3三个数中,随机抽取两个数相乘,积是正数的概率是( )
A. 0 B. C. D. 1
4.将一个转盘分成6等份,分别是红、黄、蓝、绿、白、黑,转动转盘两次,两次能配成“紫色”的概率是________(红色和蓝色配成紫色).
B
课堂练习
5.点M(x , y)可以在数字﹣1,0,1,2中任意选取. 试求:
(1)点M在第二象限内的概率.
(2)点M不在直线y=﹣2x+3上的概率
解:利用表格列出所有可能的结果:
-1 0 1 2
-1 (-1, -1) (0, -1) (1, -1) (2, -1)
0 (-1, 0) (0, 0) (1, 0) (2, 0)
1 (-1, 1) (0, 1) (1, 1) (2, 1)
2 (-1, 2) (0, 2) (1, 2) (2, 2)
x
y
课堂练习
-1 0 1 2
-1 (-1, -1) (0, -1) (1, -1) (2, -1)
0 (-1, 0) (0, 0) (1, 0) (2, 0)
1 (-1, 1) (0, 1) (1, 1) (2, 1)
2 (-1, 2) (0, 2) (1, 2) (2, 2)
x
y
课堂练习
课堂小结
第四部分
PART 04
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
试验出现各种结果的个数是有限个.
用列表法求概率适用的对象是:
试验涉及两个因素或分两步完成,如掷两个骰子,抽两张卡片,两次摸球等.
课堂小结
1.从课后习题中选取;
2.完成练习册本课时的习题.
课后作业
第四章 投影与视图 4.2.2
概率及其计算
湘教版(2024)九年级下册数学课件
4.2.2.1 用列表法求概率
01
新课导入
03
课堂练习
02
新课讲解
04
课堂小结
目录
新课导入
第一部分
PART 01
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
活动1:一枚硬币连续掷两次,求下列事件概率.
(1)两次全部正面朝上;
(2)两次全部反面朝上;
(3)一次正面朝上,一次反面朝上.
思考:解决上述问题,能否用一个表格先列举出所有可能结果,再解题呢?
新课导入
正 反
正 正正 正反
反 反正 反反
第二次
第一次
活动1:一枚硬币连续掷两次,求下列事件概率.
(1)两次全部正面朝上;
(2)两次全部反面朝上;
(3)一次正面朝上,一次反面朝上.
若能先列出表格,列举出试验的所有结果,再求确定事件的概率,是否要简捷一些.
新课导入
新课讲解
第二部分
PART 02
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
李明和刘英各掷一枚骰子,如果两枚骰子的点数之和为奇数,则李明赢;如果两枚骰子的点数之和为偶数,刘英赢. 这个游戏对双方公平吗?
新课讲解
游戏双方公平是指双发获胜的可能性相等,各掷一枚骰子,可能出现的结果数目较多,为不重不漏地列出所有可能的结果,通常采用列表法.
新课讲解
从表中可以看出,所有可能结果共有36个. 由于骰子是均匀的,这些结果出现的可能性相等.
新课讲解
满足两枚骰子的点数为偶数的可能结果有18个(表中的蓝色),两枚骰子的点数为奇数的可能结果有18个(表中的红色). 因此,
P(点数之和为偶数) .
P(点数之和为奇数) .
由此可见,这个游戏对双方而言是公平的.
新课讲解
如图,袋中装有大小和质地都相同的4个球:2红2白. 从中依次任意取出2个球(第1次取出的球不放回袋中), 求下列事件的概率:
A:取出的2个球同色;
B:取出2个白球.
新课讲解
解:用R1,R2表示两红球; 用W1,W2表示两白球;
利用表格列出所有可能的结果:
R1 R2 W1 W2
R1 × (R1, R2) (R1, W1) (R1, W2)
R2 (R2, R1) × (R2, W1) (R2, W2)
W1 (W1, R1) (W1, R2) × (W1, W2)
W2 (W2, R1) (W2, R2) (W2, W1) ×
第1次
第2次
共有_______个可能结果.
12
新课讲解
A:取出的2个球同色
______________________________________(共____种);
B:取出的2个白球
______________________________________(共____种);
(R1, R2)
(R2, R1)
(W1, W2)
(W2, W1)
4
(W1, W2)
(W2, W1)
2
新课讲解
如图,袋中装有大小和质地都相同的4个球:2红2白. 从中依次任意取出2个球(第1次取出的球不放回袋中), 求下列事件的概率:
A:取出的2个球同色;
B:取出2个白球.
新课讲解
如图,袋中装有大小和质地都相同的4个球:2红2白. 从中依次任意取出2个球(第1次取出的球放回袋中), 求下列事件的概率:
A:取出的2个球同色;
B:取出2个白球.
新课讲解
解:用R1,R2表示两红球; 用W1,W2表示两白球;
利用表格列出所有可能的结果:
R1 R2 W1 W2
R1 (R1, R1) (R1, R2) (R1, W1) (R1, W2)
R2 (R2, R1) (R2, R2) (R2, W1) (R2, W2)
W1 (W1, R1) (W1, R2) (W1, W1) (W1, W2)
W2 (W2, R1) (W2, R2) (W2, W1) (W2, W2)
第1次
第2次
新课讲解
试验出现各种结果的个数是有限个.
用列表法求概率适用的对象是:
试验涉及两个因素或分两步完成,如掷两个骰子,抽两张卡片,两次摸球等.
当试验为摸球或抽卡片时,一定要分清第一次摸球或抽卡片后,“球”与“卡”是否放回,即“放回”与“不放回”结果是不同的.
归纳小结
1.如图,有三条绳子穿过一块木板,姐妹两人分别站在木板的左、右两边,各选该边的一段绳子.若每边每段绳子被选中的机会相等, 则两人选到同一条绳子的概率为多少?
新课讲解
解:用A1,A2,A3示三条绳子,
利用表格列出所有可能的结果:
A1 A2 A3
A1 (A1, A1) (A1, A2) (A1, A3)
A2 (A2, A1) (A2, A2) (A2, A3)
A3 (A3, A1) (A3, A2) (A3, A3)
姐姐
妹妹
共有9个可能结果,其中两人选到同一条绳子的情况有3种,
新课讲解
2.小军同时抛掷两枚骰子,求两枚骰子点数之和小于7的概率.
解:利用表格列出所有可能的结果:
新课讲解
共有36个可能结果,其中两枚骰子点数之和小于7的结果有15种,
新课讲解
课堂练习
第三部分
PART 03
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
1.从1,2,3,4,5五个数中任意取出2个数做加法,其和为偶数的概率是( )
A. B. C. D.
C
课堂练习
2.均匀的正四面体的各面上依次标有1,2,3,4四个数字,同时抛掷两个这样的正四面体,着地的一面数字之和为5的概率是( )
A. B. C. D.
B
课堂练习
3.从1,2,﹣3三个数中,随机抽取两个数相乘,积是正数的概率是( )
A. 0 B. C. D. 1
4.将一个转盘分成6等份,分别是红、黄、蓝、绿、白、黑,转动转盘两次,两次能配成“紫色”的概率是________(红色和蓝色配成紫色).
B
课堂练习
5.点M(x , y)可以在数字﹣1,0,1,2中任意选取. 试求:
(1)点M在第二象限内的概率.
(2)点M不在直线y=﹣2x+3上的概率
解:利用表格列出所有可能的结果:
-1 0 1 2
-1 (-1, -1) (0, -1) (1, -1) (2, -1)
0 (-1, 0) (0, 0) (1, 0) (2, 0)
1 (-1, 1) (0, 1) (1, 1) (2, 1)
2 (-1, 2) (0, 2) (1, 2) (2, 2)
x
y
课堂练习
-1 0 1 2
-1 (-1, -1) (0, -1) (1, -1) (2, -1)
0 (-1, 0) (0, 0) (1, 0) (2, 0)
1 (-1, 1) (0, 1) (1, 1) (2, 1)
2 (-1, 2) (0, 2) (1, 2) (2, 2)
x
y
课堂练习
课堂小结
第四部分
PART 04
your content is entered here, or by copying your text, select paste in this box and choose to retain only text. your content is typed here
试验出现各种结果的个数是有限个.
用列表法求概率适用的对象是:
试验涉及两个因素或分两步完成,如掷两个骰子,抽两张卡片,两次摸球等.
课堂小结
1.从课后习题中选取;
2.完成练习册本课时的习题.
课后作业
