11.1.2不等式的性质 课件(共19张PPT)2024--2025学年人教版七年级数学下册
文档属性
| 名称 | 11.1.2不等式的性质 课件(共19张PPT)2024--2025学年人教版七年级数学下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 326.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-15 16:18:12 | ||
图片预览




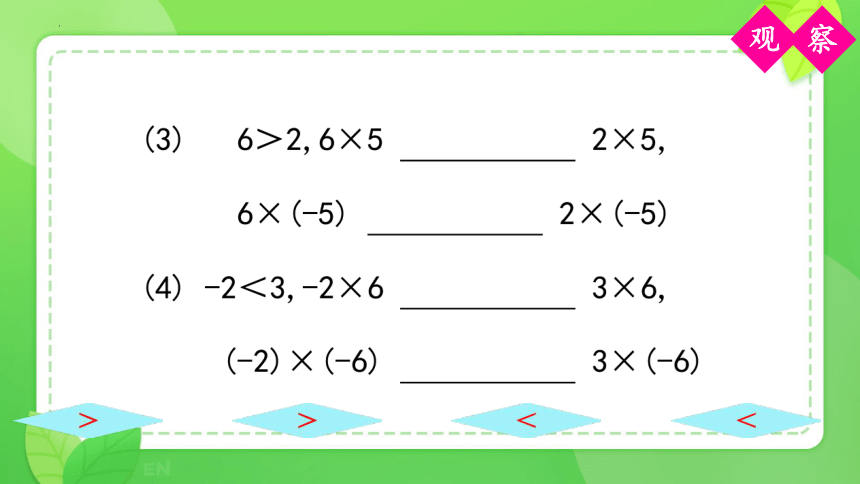


文档简介
(共19张PPT)
第十一章 不等式与不等式组
11.1 不等式
11.1.2 不等式的性质
观
察
这个结论正确吗?
探究新知
当不等式两边加或减同一个数(正数或负数)时,不等号的方向不变.
8 5, 8+2 5+2, 8-2 5-2.
-5 -1, -5+2 -1+2, -5-2 -1-2.
-5 5, -5+2 5+2, -5-2 5-2.
>
<
<
由结果可知我们的猜想正确.
验
证
不等式两边加(或减)同一个数(或式子),不等号的方向不变.
如果a>b,那么a±c>b±c.
不等式的性质1
归
纳
观
察
8 5, 8×2 5×2, 8×(-4) 5×(-4)
-5 -1,(-5)×3 (-1)×3,(-5)×(-2) (-1)×(-2)
这个结论正确吗?
探究新知
当不等式两边乘同一个正数时,不等号的方向不变;而乘同一个负数时,不等号的方向改变.
对于除法,这个性质适用吗?
>
<
由结果可知我们的猜想正确.
猜
想
探究新知
8 4, 8÷2 4÷2, 8÷(-4) 4÷(-4)
-10 -5,(-10)÷3 (-5)÷3,(-10)÷(-2) (-5)÷(-2)
>
<
由结果可知乘法的性质除法也适用.
验
证
(1) a - 7____b - 7;
(2) a÷6____b÷6
(3) 0.1a____0.1b;
(4) -4a____-4b
(5) 2a+3____2b+3;
(6)(m2+1)a____ (m2+1)b(m为常数)
练一练
1.设a>b,用“<”“>”填空并回答是根据不等式的哪一条基本性质.
2.已知a<0,用“<”“>”填空:
(1)a+2 ____2; (2)a-1 _____-1;
(3)3a______0; (4) ______0;
(5)a2_____0; (6)a3______0;
(7)a-1_____0; (8)|a|______0.
>
>
>
>
>
>
>
>
<
<
<
<
<
<
思考: 等式有对称性及传递性,那么不等式具有对称性和传递性吗
x>5 5性质4(对称性):如果a>b,那么b由8如:8<10,10<15 ,8 < 15.
性质5(同向传递性):如果a>b,b>c,那么a>c.
例3 如果不等式 (a+1)x<a+1可变形为 x>1,那么a 必须满足________.
解析:根据不等式的基本性质可判断,a+1为负数,即a+1<0,可得 a<-1.
方法总结:只有当不等式的两边都乘(或除以)一个负数时,不等号的方向才改变.
例4 利用不等式的性质解下列不等式:
(1) x-7>26; (2) 3x<2x+1;
(3) >50; (4) -4x>3.
利用不等式的性质解简单的不等式
目标
方法:不等式的性质1~3
(1) x-7>26;
(1)解 :为了使不等式x-7>26中不等号的一边变为x,根据不等式的性质1,不等式两边都加7,不等号的方向不变,得
x-7+7﹥26+7,即x﹥33.
这个不等式的解集在数轴上的表示如图所示:
(2) 3x<2x+1;
(2)解:为了使不等式3x<2x+1中不等号的一边变为x,根 据等式的性质1,不等式两边都减去2x,不等号的方向不变,得 .
3x-2x<2x+1-2x ,即 x<1
这个不等式的解集在数轴上的表示如图所示:
(3)解:为了使不等式中不等号的一边变为x,根据不等式的性质2,不等式的两边都除以 ,不等号的方向不变,得.
x>75
这个不等式的解集在数轴上的表示如图所示:
(4)解:为了使不等式-4x>3中的不等号的一边变为x,根据不等式的性质3,不等式两边都除以-4,不等号的方向改变,得
这个不等式的解集在数轴上的表示如图所示:
在不等式-4x+5>9的两边都减去5,得
-4x > 4
在不等式-4x> 4的两边都除以-4,得
x > -1
下面是某同学根据不等式的性质做的一道题:
请问他做对了吗?如果不对,请改正.
x<-1
1. 已知a < b,用“>”或“<”填空:
(1)a +12 b +12 ;
(2)b-10 a -10 .
2. 把下列不等式化为x>a或x(1)5>3+x;
(2)2x<x+6.
<
<
解:x < 2
解:x < 6
3.利用不等式的性质解下列不等式,并在数轴上表示其解集.
(1)x-5 > -1
(2)-2x > 3
(3)7x < 6x-6
x>4
x<-6
不等式两边加(或减)同一个数(或式子),不等号的方向不变.
不等式的两边都乘(或除以)同一个正数,不等号的方向不变.
不等式的两边都乘(或除以)同一个负数,不等号的方向改变.
第十一章 不等式与不等式组
11.1 不等式
11.1.2 不等式的性质
观
察
这个结论正确吗?
探究新知
当不等式两边加或减同一个数(正数或负数)时,不等号的方向不变.
8 5, 8+2 5+2, 8-2 5-2.
-5 -1, -5+2 -1+2, -5-2 -1-2.
-5 5, -5+2 5+2, -5-2 5-2.
>
<
<
由结果可知我们的猜想正确.
验
证
不等式两边加(或减)同一个数(或式子),不等号的方向不变.
如果a>b,那么a±c>b±c.
不等式的性质1
归
纳
观
察
8 5, 8×2 5×2, 8×(-4) 5×(-4)
-5 -1,(-5)×3 (-1)×3,(-5)×(-2) (-1)×(-2)
这个结论正确吗?
探究新知
当不等式两边乘同一个正数时,不等号的方向不变;而乘同一个负数时,不等号的方向改变.
对于除法,这个性质适用吗?
>
<
由结果可知我们的猜想正确.
猜
想
探究新知
8 4, 8÷2 4÷2, 8÷(-4) 4÷(-4)
-10 -5,(-10)÷3 (-5)÷3,(-10)÷(-2) (-5)÷(-2)
>
<
由结果可知乘法的性质除法也适用.
验
证
(1) a - 7____b - 7;
(2) a÷6____b÷6
(3) 0.1a____0.1b;
(4) -4a____-4b
(5) 2a+3____2b+3;
(6)(m2+1)a____ (m2+1)b(m为常数)
练一练
1.设a>b,用“<”“>”填空并回答是根据不等式的哪一条基本性质.
2.已知a<0,用“<”“>”填空:
(1)a+2 ____2; (2)a-1 _____-1;
(3)3a______0; (4) ______0;
(5)a2_____0; (6)a3______0;
(7)a-1_____0; (8)|a|______0.
>
>
>
>
>
>
>
>
<
<
<
<
<
<
思考: 等式有对称性及传递性,那么不等式具有对称性和传递性吗
x>5 5
性质5(同向传递性):如果a>b,b>c,那么a>c.
例3 如果不等式 (a+1)x<a+1可变形为 x>1,那么a 必须满足________.
解析:根据不等式的基本性质可判断,a+1为负数,即a+1<0,可得 a<-1.
方法总结:只有当不等式的两边都乘(或除以)一个负数时,不等号的方向才改变.
例4 利用不等式的性质解下列不等式:
(1) x-7>26; (2) 3x<2x+1;
(3) >50; (4) -4x>3.
利用不等式的性质解简单的不等式
目标
方法:不等式的性质1~3
(1) x-7>26;
(1)解 :为了使不等式x-7>26中不等号的一边变为x,根据不等式的性质1,不等式两边都加7,不等号的方向不变,得
x-7+7﹥26+7,即x﹥33.
这个不等式的解集在数轴上的表示如图所示:
(2) 3x<2x+1;
(2)解:为了使不等式3x<2x+1中不等号的一边变为x,根 据等式的性质1,不等式两边都减去2x,不等号的方向不变,得 .
3x-2x<2x+1-2x ,即 x<1
这个不等式的解集在数轴上的表示如图所示:
(3)解:为了使不等式中不等号的一边变为x,根据不等式的性质2,不等式的两边都除以 ,不等号的方向不变,得.
x>75
这个不等式的解集在数轴上的表示如图所示:
(4)解:为了使不等式-4x>3中的不等号的一边变为x,根据不等式的性质3,不等式两边都除以-4,不等号的方向改变,得
这个不等式的解集在数轴上的表示如图所示:
在不等式-4x+5>9的两边都减去5,得
-4x > 4
在不等式-4x> 4的两边都除以-4,得
x > -1
下面是某同学根据不等式的性质做的一道题:
请问他做对了吗?如果不对,请改正.
x<-1
1. 已知a < b,用“>”或“<”填空:
(1)a +12 b +12 ;
(2)b-10 a -10 .
2. 把下列不等式化为x>a或x
(2)2x<x+6.
<
<
解:x < 2
解:x < 6
3.利用不等式的性质解下列不等式,并在数轴上表示其解集.
(1)x-5 > -1
(2)-2x > 3
(3)7x < 6x-6
x>4
x<-6
不等式两边加(或减)同一个数(或式子),不等号的方向不变.
不等式的两边都乘(或除以)同一个正数,不等号的方向不变.
不等式的两边都乘(或除以)同一个负数,不等号的方向改变.
同课章节目录
