11.1.2不等式的性质--课件(32张PPT)2024--2025学年人教版七年级数学下册
文档属性
| 名称 | 11.1.2不等式的性质--课件(32张PPT)2024--2025学年人教版七年级数学下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 453.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-15 18:23:18 | ||
图片预览








文档简介
(共32张PPT)
第十一章 不等式与不等式组
11.1 不等式
11.1.2 不等式的性质
第1课时 不等式的性质
预习检测
例1 利用不等式的性质解下列不等式:
(1)x-7>26; (2)3x<2x+1;
(3) x>50; (4)-4x>3.
分析
解不等式,就是借助不等式的性质使不等式逐步化为x>a或x(1)x-7>26
要利用不等式的性质1.
解这个不等式要利用哪个性质?
(2)3x<2x+1
解:
根据不等式的性质1,不等式两边加7,不等号的方向不变,所以
x-7+7>26+7
x>33
解:
根据不等式的性质1,不等式两边减2x,不等号的方向不变,所以
3x+2x<2x+1-2x
x<1
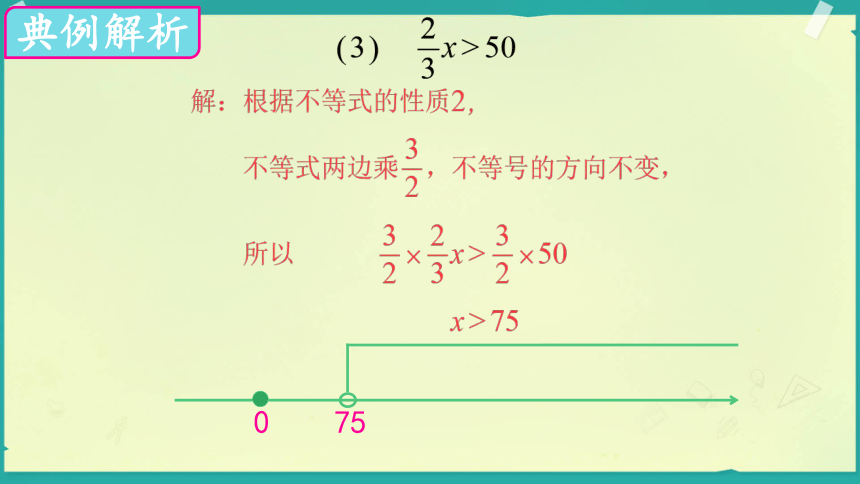
(3) x>50
(4)-4x>3
根据不等式的性质2,不等式两边乘 ,不等号的方向不变,所以
解:
解:
x>50
x>75
根据不等式的性质3,不等式两边除以-4,不等号的方向改变,所以
x<
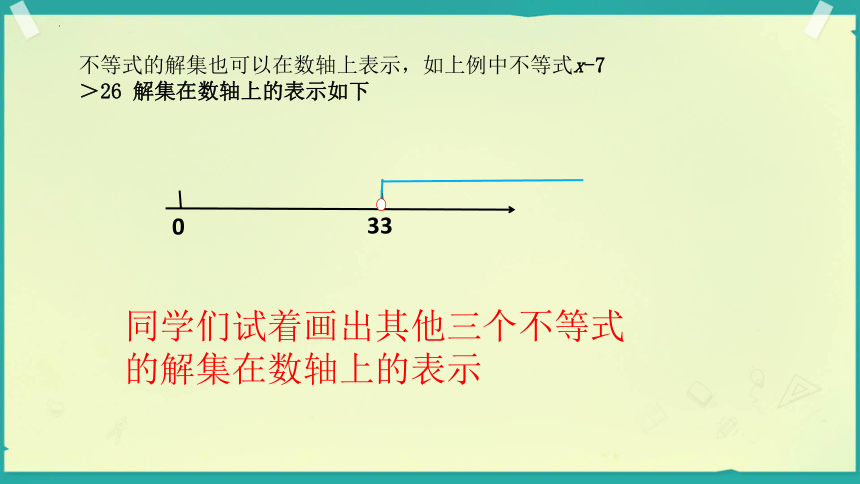
不等式的解集也可以在数轴上表示,如上例中不等式x-7>26 解集在数轴上的表示如下
0
33
同学们试着画出其他三个不等式的解集在数轴上的表示
学习目标
1.进一步理解不等式的性质.
2.了解含有符号“≥”和“≤”的不等式.
知识回顾
不等式具有哪些性质?
不等式 文字语言 符号语言
性质1 不等式两边加(或减)同一个数(或式子),不等号的方向不变. 如果a>b,那么a±c>b±c.
性质2 不等式的两边乘(或除以)同一个正数,不等号的方向不变.
性质3 不等式的两边乘(或除以)同一个负数,不等号的方向改变.
典例解析
例1 利用不等式的性质解下列不等式:
解不等式,就是借助不等式的性质使不等式逐步化为x>a或x典例解析
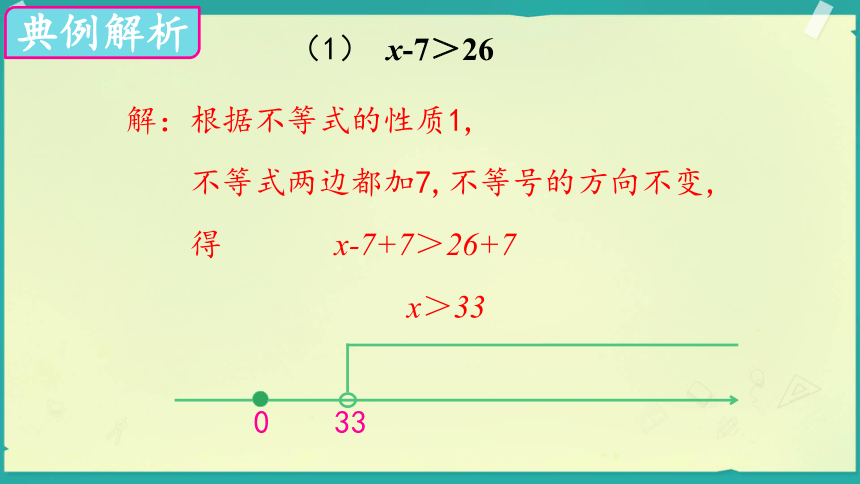
(1) x-7>26
解:根据不等式的性质1,
不等式两边都加7,不等号的方向不变,
得 x-7+7>26+7
x>33
0 33
典例解析
(2) 3x<2x+1
解:根据不等式的性质1,
不等式两边减2x,不等号的方向不变,
得 3x-2x<2x+1-2x
x<1
0 1
典例解析
0 75
典例解析
(4) -x>3
(3)(4)的求解过程,类似于解方程两边都除以未知数的系数(未知数系数化为1),解不等式时要注意未知数系数的正负,以决定是否改变不等号的方向.
典例解析
探究新知
符号“≥”与“>”的意思有什么区别?
“≥”表示包含某个数值,“>”表示不包含该数值.
在表示两个数量大小关系时,我们会经常用到像a≥b或a≤b这样的式子,如一天内的温度变化t≥19℃且t≤28℃.
“≤”与“<”呢?
探究新知
种类 符号 实际意义 读法 举例
小于号 < 小于、不足、少于、低于 小于 1+1<3
大于号 > 大于、超过、高出、多于 大于 20+8>16
小于等于号 ≤ 不大于、不超过、至多 小于或等于 (不大于) x≤4
大于等于号 ≥ 不小于、不低于、至少 大于或等于 (不小于) x≥8
不等号 ≠ 不等于 不等于 10≠8
哪些符号可以表示不等关系?
探究新知
它们是否具有与前面所说的不等式的性质类似的性质呢?
不等式的性质
运用新知
例2 某长方体形状的容器长5cm,宽3cm,高10cm.
容器内原有水的高度为3cm,现准备向它继续注
水.用V(单位cm3)表示新注入水的体积,写出
V的取值范围.
学习了用不等式的性质解不等式,你现在能解决这个问题了吗
运用新知
分析:要求新注入水的体积范围,那就要求出容器的总体
积和已经被占用的体积.
容器的总体积为: 3×5×10
被占用的容器的体积为: 3×5×3
根据题意有: V+3×5×3 ≤ 3×5×10
运用新知
V+3×5×3 ≤ 3×5×10
V≤ 105
考虑到实际意义,新注入水的体积V不能是负数,因
此V的取值范围是:V ≥ 0且V ≤ 105.
这样就可以了吗?
不是.在利用不等式解决实际问题时一定要考虑未知数的实际意义.
运用新知
实心圆表示不等式的取值范围包括这个数,空心圆表示不等式的取值范围不包括这个数.
V ≥ 0且V ≤ 105
在数轴上表示V的取值范围:
0 105
二、不等式的实际应用
某长方体形状的容器长5cm,宽3cm,高10cm.容器内原有水的高度为3cm,现准备向它继续注水.用V(单位cm3)表示新注入水的体积,写出V的取值范围.
学习了用不等式的性质解不等式,你现在能解决这个问题了吗?
分析
要求新注入水的体积范围,那就要求出容器的总体积和已经被占用的体积.
容器的总体积为:
3×5×10
被占用的容器的体积为:
3×5×3
根据题意有:
V+3×5×3 ≤ 3×5×10
V+3×5×3≤3×5×10
V≤105
不是.在利用不等式解决实际问题时一定要考虑未知数的实际意义.
这样就可以了吗?
V+3×5×3≤3×5×10
V ≥ 0且V ≤ 105
考虑到实际意义,新注入水的体积V不能是负数,因此V的取值范围是:
V≤105
在数轴上表示出来为:
0
105
0
105
这里是实心圆表示,那实心圆与空心圆有什么区别呢?
实心圆表示不等式的取值范围包括这两个数,空心圆表示不等式的取值范围不包括这两个数.
小
结
利用不等式性质解不等式的注意事项
1.在运用性质3时,要特别注意:不等式两边都乘以或除以同一个负数时,要改变不等号的方向。
2.要注意区分“大于”“不大于”“小于”“不小于”等数学语言的使用,并把这些表示不等关系的语言用数学符号准确地表达出来。
3.在数轴上表示解集应注意的问题:方向、空心圆圈或实心圆点。
1. 不等式3-2x≤7的解集是( )
A. x ≥-2 B. x ≤-2
C. x ≤-5 D. x ≥-5
A
练习
2.不等式 x - 2 ≥ 0 的解集在数轴上表示正确的是( )
B
A
B
C
D
3.小华拿27元钱购买圆珠笔和练习册,已知一本练习册2元,一支圆珠笔1元,他买了4本练习册,x 支圆珠笔,则关于 x 的不等式表示正确的是( )
B
A.2×4+x<27 B.2×4+x≤27
C.2x+4≤27 D.2x+4≥27
课堂小结
1.如何利用不等式的性质解简单不等式?
2.依据不等式性质3解不等式时应注意什么?
3.请说明符号“≥”和“≤”的含义?
课后作业
教科书 习题9.1 第5、7、8题.
第十一章 不等式与不等式组
11.1 不等式
11.1.2 不等式的性质
第1课时 不等式的性质
预习检测
例1 利用不等式的性质解下列不等式:
(1)x-7>26; (2)3x<2x+1;
(3) x>50; (4)-4x>3.
分析
解不等式,就是借助不等式的性质使不等式逐步化为x>a或x
要利用不等式的性质1.
解这个不等式要利用哪个性质?
(2)3x<2x+1
解:
根据不等式的性质1,不等式两边加7,不等号的方向不变,所以
x-7+7>26+7
x>33
解:
根据不等式的性质1,不等式两边减2x,不等号的方向不变,所以
3x+2x<2x+1-2x
x<1
(3) x>50
(4)-4x>3
根据不等式的性质2,不等式两边乘 ,不等号的方向不变,所以
解:
解:
x>50
x>75
根据不等式的性质3,不等式两边除以-4,不等号的方向改变,所以
x<
不等式的解集也可以在数轴上表示,如上例中不等式x-7>26 解集在数轴上的表示如下
0
33
同学们试着画出其他三个不等式的解集在数轴上的表示
学习目标
1.进一步理解不等式的性质.
2.了解含有符号“≥”和“≤”的不等式.
知识回顾
不等式具有哪些性质?
不等式 文字语言 符号语言
性质1 不等式两边加(或减)同一个数(或式子),不等号的方向不变. 如果a>b,那么a±c>b±c.
性质2 不等式的两边乘(或除以)同一个正数,不等号的方向不变.
性质3 不等式的两边乘(或除以)同一个负数,不等号的方向改变.
典例解析
例1 利用不等式的性质解下列不等式:
解不等式,就是借助不等式的性质使不等式逐步化为x>a或x
(1) x-7>26
解:根据不等式的性质1,
不等式两边都加7,不等号的方向不变,
得 x-7+7>26+7
x>33
0 33
典例解析
(2) 3x<2x+1
解:根据不等式的性质1,
不等式两边减2x,不等号的方向不变,
得 3x-2x<2x+1-2x
x<1
0 1
典例解析
0 75
典例解析
(4) -x>3
(3)(4)的求解过程,类似于解方程两边都除以未知数的系数(未知数系数化为1),解不等式时要注意未知数系数的正负,以决定是否改变不等号的方向.
典例解析
探究新知
符号“≥”与“>”的意思有什么区别?
“≥”表示包含某个数值,“>”表示不包含该数值.
在表示两个数量大小关系时,我们会经常用到像a≥b或a≤b这样的式子,如一天内的温度变化t≥19℃且t≤28℃.
“≤”与“<”呢?
探究新知
种类 符号 实际意义 读法 举例
小于号 < 小于、不足、少于、低于 小于 1+1<3
大于号 > 大于、超过、高出、多于 大于 20+8>16
小于等于号 ≤ 不大于、不超过、至多 小于或等于 (不大于) x≤4
大于等于号 ≥ 不小于、不低于、至少 大于或等于 (不小于) x≥8
不等号 ≠ 不等于 不等于 10≠8
哪些符号可以表示不等关系?
探究新知
它们是否具有与前面所说的不等式的性质类似的性质呢?
不等式的性质
运用新知
例2 某长方体形状的容器长5cm,宽3cm,高10cm.
容器内原有水的高度为3cm,现准备向它继续注
水.用V(单位cm3)表示新注入水的体积,写出
V的取值范围.
学习了用不等式的性质解不等式,你现在能解决这个问题了吗
运用新知
分析:要求新注入水的体积范围,那就要求出容器的总体
积和已经被占用的体积.
容器的总体积为: 3×5×10
被占用的容器的体积为: 3×5×3
根据题意有: V+3×5×3 ≤ 3×5×10
运用新知
V+3×5×3 ≤ 3×5×10
V≤ 105
考虑到实际意义,新注入水的体积V不能是负数,因
此V的取值范围是:V ≥ 0且V ≤ 105.
这样就可以了吗?
不是.在利用不等式解决实际问题时一定要考虑未知数的实际意义.
运用新知
实心圆表示不等式的取值范围包括这个数,空心圆表示不等式的取值范围不包括这个数.
V ≥ 0且V ≤ 105
在数轴上表示V的取值范围:
0 105
二、不等式的实际应用
某长方体形状的容器长5cm,宽3cm,高10cm.容器内原有水的高度为3cm,现准备向它继续注水.用V(单位cm3)表示新注入水的体积,写出V的取值范围.
学习了用不等式的性质解不等式,你现在能解决这个问题了吗?
分析
要求新注入水的体积范围,那就要求出容器的总体积和已经被占用的体积.
容器的总体积为:
3×5×10
被占用的容器的体积为:
3×5×3
根据题意有:
V+3×5×3 ≤ 3×5×10
V+3×5×3≤3×5×10
V≤105
不是.在利用不等式解决实际问题时一定要考虑未知数的实际意义.
这样就可以了吗?
V+3×5×3≤3×5×10
V ≥ 0且V ≤ 105
考虑到实际意义,新注入水的体积V不能是负数,因此V的取值范围是:
V≤105
在数轴上表示出来为:
0
105
0
105
这里是实心圆表示,那实心圆与空心圆有什么区别呢?
实心圆表示不等式的取值范围包括这两个数,空心圆表示不等式的取值范围不包括这两个数.
小
结
利用不等式性质解不等式的注意事项
1.在运用性质3时,要特别注意:不等式两边都乘以或除以同一个负数时,要改变不等号的方向。
2.要注意区分“大于”“不大于”“小于”“不小于”等数学语言的使用,并把这些表示不等关系的语言用数学符号准确地表达出来。
3.在数轴上表示解集应注意的问题:方向、空心圆圈或实心圆点。
1. 不等式3-2x≤7的解集是( )
A. x ≥-2 B. x ≤-2
C. x ≤-5 D. x ≥-5
A
练习
2.不等式 x - 2 ≥ 0 的解集在数轴上表示正确的是( )
B
A
B
C
D
3.小华拿27元钱购买圆珠笔和练习册,已知一本练习册2元,一支圆珠笔1元,他买了4本练习册,x 支圆珠笔,则关于 x 的不等式表示正确的是( )
B
A.2×4+x<27 B.2×4+x≤27
C.2x+4≤27 D.2x+4≥27
课堂小结
1.如何利用不等式的性质解简单不等式?
2.依据不等式性质3解不等式时应注意什么?
3.请说明符号“≥”和“≤”的含义?
课后作业
教科书 习题9.1 第5、7、8题.
同课章节目录
