11.1.1不等式及其解集--课件 (41张PPT) 2024-2025学年人教版七年级数学下册
文档属性
| 名称 | 11.1.1不等式及其解集--课件 (41张PPT) 2024-2025学年人教版七年级数学下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1019.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-15 18:28:48 | ||
图片预览











文档简介
(共41张PPT)
七年级·数学·人教版·下册
导学案课堂同步导学
11.1 不等式
学 业 要 求 1.结合具体问题,了解不等式的意义,探索不等式的基本性质.
2.能用不等式的基本性质对不等式进行变形.
3.能解数字系数的一元一次不等式,并能在数轴上表示出解集.
4.会用数轴确定两个一元一次不等式组成的不等式组的解集.
5.能根据具体问题中的数量关系,列出一元一次不等式,解决简单的实际问题,建立模型观念
大任务
类比等式和方程,探索不等式的性质,学习一元一次不等式(组)及其解法,并利用这些知识解决一些问题,感受不等式在研究不等关系问题中的重要作用
子任务
本章学习约需8课时,具体分配如下:
11.1 不等式 3课时
11.2 一元一次不等式 3课时
11.3 一元一次不等式组 1课时
章节复习课 1课时
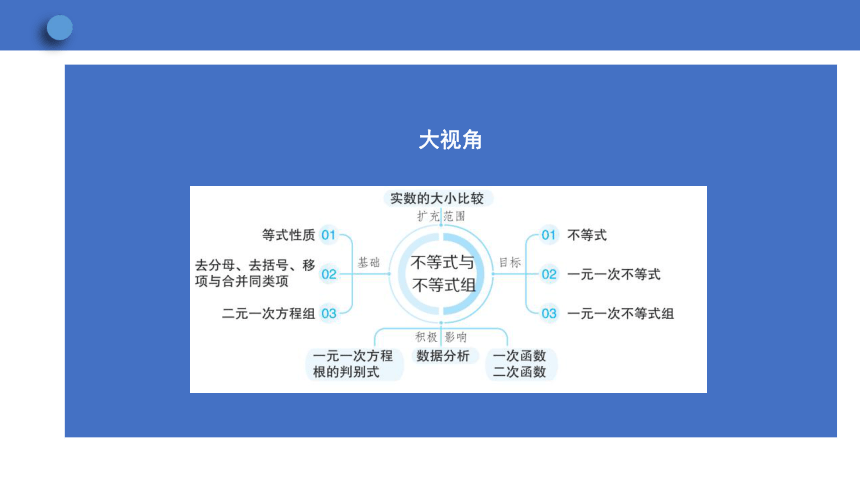
大视角
学法建议
1.学习时应对基本性质深入理解,认真辨别不等式性质与等式基本性质的异同、不等式的解或解集与方程的解的区别,做题时要认真审题,抓住关键.
2.学习时要认真研究不等式(组)的特殊解,将不等式的知识与方程等相关知识结合在一起训练,这样有利于提高解题能力.
3.注重应用,培养能力.最好要找出典型题的解法规律和方法,提高分析问题和解决问题的能力
11.1 不等式
11.1.1 不等式及其解集
1.会判断一个式子是不是不等式.
2.会把不等式的解集表示到数轴上.
3.经历“把实际问题抽象为不等式”的过程,进一步体会数学建模的思想方法.
不等式解集的表示.
不等式解集的确定.
问题:现实生活中,数量之间存在着相等与不相等的关系.对于不相等的关系问题,我们该如何用式子来表示它们呢
例如,小明的体重为45 kg,小聪的体重为46 kg,则我们可以用不等号“>”或“<”来表示他们体重之间的关系.
如:46>45或45<46.
1.什么叫等式
表示相等关系的式子叫作等式.
2.什么叫方程
含有未知数的等式叫方程.
3.数轴的三要素是什么
原点、正方向、单位长度.
1.若x●4是不等式,则符号“●”可以是 ( )
A.+ B.= C.÷ D.≥
D
2.判断下列说法是否正确,对的打“√”,错的打“×”.
(1)x=2是不等式2x+1<7的解. ( )
(2)满足x<3的x的值有无数个,在数轴上无法表示. ( )
×
√
不等式的概念
阅读课本本课时“例1”前面的内容,回答下列问题:
1.什么叫等式 什么叫不等式
用等号连接表示相等关系的式子叫作等式;用符号“>”或“<”表示不等关系的式子叫作不等式.用“≠”表示不等关系的式子也是不等式.
2.我们用哪些符号表示不等关系
>、<、≠.
下列各式中:①-5<7;②3y-6>0;③a=6;④2x-3y;⑤a≠2;⑥7y-6>y+2.是不等式的有 ( )
A.2个 B.3个 C.4个 D.5个
C
·导学建议·
教学中,老师可通过生活中的具体实例建立不等式模型,逐步向学生渗透数学建模的思想.
不等式的解、解集,解不等式
阅读课本本课时“例1”至“练习”前的内容,解决下列问题.
1.下列各数中,能使不等式3x>6成立的数有哪些
-2,-1,0,2,3,5,300.
这些数中使不等式3x>6成立的数有3,5,300.
2.使3x>6成立的x的值有多少个 当x满足什么条件时,不等式3x>6成立
无数个.x>2.
3.怎样在数轴上表示x的取值范围
如图所示
(1)使不等式成立的 叫作不等式的解,不等式的解一般有 个.
(2)一般地,一个含有未知数的不等式的 ,组成这个不等式的解集.
(3) 叫作解不等式.
(4)在数轴上表示不等式的解集的方法:
不等号是大于时,射线向 画,不等号是小于时,射线向 画.有等号时画 点,无等号时画 .
空心圆圈
右
求不等式的解集的过程
所有的解
未知数的值
无数
左
实心
·导学建议·
此活动环节,要让学生充分发表意见,并通过计算、动手验证、动脑思考,初步体会不等式解的意义以及不等式解与方程解的不同之处.
用不等式表示数量关系
例1 下列说法中正确的是 ( )
A.x=1是不等式-2x<1的解
B.x=-1是不等式-2x<1的解
C.x=-是不等式-2x<1的解
D.不等式-2x<1的解集是x=1
A
·导学建议·
通过题型一的学习,让学生明白不等式的解集包括了不等式的每个解,解集中任何一个数都是不等式的一个解.
变式训练 用不等式表示下列语句.
(1)m的与n的的差是正数;(2)y与1的和小于y的;(3)y的40%与5的差小于0.
读懂数或字母间的数量关系→找准不等关系→列不等式.
解:(1)m-n>0;(2)y+1不等式的解集
例2 对于不等式x+3>6,完成以下问题:
(1)x=1,x=2,x=3,x=4,x=5,x=6,哪些是x+3>6的解 哪些不是
(2)不等式x+3>6的解集是什么 并在数轴上表示出来.
解:(1)x=4,x=5,x=6是不等式的解,x=1,x=2,x=3不是.
(2)x>3.在数轴上表示略.
方法归纳交流 1.验证一个未知数的值是不是不等式的解的方法:将未知数的值代入到不等式中,使不等式成立,则未知数的值即是不等式的解.否则不是.
2.在数轴上表示不等式的解集时,空心圆圈表示解集不包括这个点,注意画线的方向问题.
1.下列各式中,不是不等式的是 ( )
A.2x≠1 B.-5<1
C.4x-1<6 D.y=x-4
D
2.用含x的不等式表示下列数轴所表示的解集:
(1)
(2)
(3)
(4)
解:(1)表示的解集为x>-1.
(2)表示的解集为x≥-2.
(3)表示的解集为x≤-.
(4)表示的解集为x≤-2.5.
1.如图,数轴上所示的解集用不等式表示正确的是 ( )
A.x>-2 B.x≥-2 C.x<-2 D.x≤-2
C
2.给出下列四个式子:①4<7;②a<3;③a≠0;④a>b.其中是不等式的是 ( )
A.②③ B.①②③
C.②③④ D.①②③④
D
3.请写出一个关于x的不等式,使-1,2都是它的解:
.
x-1<2(答案不唯一)
4.用不等式表示下列数量关系:
(1)m与3的和小于n;
(2)x与12的差比y的3倍大;
(3)a与b的乘积是正数.
解:(1)m+33y;(3)ab>0.
5.下列各数中:-8,-2.5,0,1,,2,-,4使不等式2x>2成立的数有 ( )
A.5个 B.4个 C.3个 D.2个
C
6.直接写出下列不等式的解集:
(1)x-3>0的解集是 ;
(2)2x<12的解集是 ;
(3)x+2<4的解集是 .
x<2
x<6
x>3
7.用不等式表示如图所示的天平的两边所给的量之间的关系.
解:40>10+2x.
8.某班去某博物馆参观,花了220元租了一辆客车,设这个班的人数为x人.
(1)如果每人交8元租车费后,还有剩余,请写出x应满足的不等式.
(2)如果每人交7元的租车费,结果还不够,这时x应满足的不等式是什么呢
解:(1)8x>220;(2)7x<220.
七年级·数学·人教版·下册
导学案课堂同步导学
11.1 不等式
学 业 要 求 1.结合具体问题,了解不等式的意义,探索不等式的基本性质.
2.能用不等式的基本性质对不等式进行变形.
3.能解数字系数的一元一次不等式,并能在数轴上表示出解集.
4.会用数轴确定两个一元一次不等式组成的不等式组的解集.
5.能根据具体问题中的数量关系,列出一元一次不等式,解决简单的实际问题,建立模型观念
大任务
类比等式和方程,探索不等式的性质,学习一元一次不等式(组)及其解法,并利用这些知识解决一些问题,感受不等式在研究不等关系问题中的重要作用
子任务
本章学习约需8课时,具体分配如下:
11.1 不等式 3课时
11.2 一元一次不等式 3课时
11.3 一元一次不等式组 1课时
章节复习课 1课时
大视角
学法建议
1.学习时应对基本性质深入理解,认真辨别不等式性质与等式基本性质的异同、不等式的解或解集与方程的解的区别,做题时要认真审题,抓住关键.
2.学习时要认真研究不等式(组)的特殊解,将不等式的知识与方程等相关知识结合在一起训练,这样有利于提高解题能力.
3.注重应用,培养能力.最好要找出典型题的解法规律和方法,提高分析问题和解决问题的能力
11.1 不等式
11.1.1 不等式及其解集
1.会判断一个式子是不是不等式.
2.会把不等式的解集表示到数轴上.
3.经历“把实际问题抽象为不等式”的过程,进一步体会数学建模的思想方法.
不等式解集的表示.
不等式解集的确定.
问题:现实生活中,数量之间存在着相等与不相等的关系.对于不相等的关系问题,我们该如何用式子来表示它们呢
例如,小明的体重为45 kg,小聪的体重为46 kg,则我们可以用不等号“>”或“<”来表示他们体重之间的关系.
如:46>45或45<46.
1.什么叫等式
表示相等关系的式子叫作等式.
2.什么叫方程
含有未知数的等式叫方程.
3.数轴的三要素是什么
原点、正方向、单位长度.
1.若x●4是不等式,则符号“●”可以是 ( )
A.+ B.= C.÷ D.≥
D
2.判断下列说法是否正确,对的打“√”,错的打“×”.
(1)x=2是不等式2x+1<7的解. ( )
(2)满足x<3的x的值有无数个,在数轴上无法表示. ( )
×
√
不等式的概念
阅读课本本课时“例1”前面的内容,回答下列问题:
1.什么叫等式 什么叫不等式
用等号连接表示相等关系的式子叫作等式;用符号“>”或“<”表示不等关系的式子叫作不等式.用“≠”表示不等关系的式子也是不等式.
2.我们用哪些符号表示不等关系
>、<、≠.
下列各式中:①-5<7;②3y-6>0;③a=6;④2x-3y;⑤a≠2;⑥7y-6>y+2.是不等式的有 ( )
A.2个 B.3个 C.4个 D.5个
C
·导学建议·
教学中,老师可通过生活中的具体实例建立不等式模型,逐步向学生渗透数学建模的思想.
不等式的解、解集,解不等式
阅读课本本课时“例1”至“练习”前的内容,解决下列问题.
1.下列各数中,能使不等式3x>6成立的数有哪些
-2,-1,0,2,3,5,300.
这些数中使不等式3x>6成立的数有3,5,300.
2.使3x>6成立的x的值有多少个 当x满足什么条件时,不等式3x>6成立
无数个.x>2.
3.怎样在数轴上表示x的取值范围
如图所示
(1)使不等式成立的 叫作不等式的解,不等式的解一般有 个.
(2)一般地,一个含有未知数的不等式的 ,组成这个不等式的解集.
(3) 叫作解不等式.
(4)在数轴上表示不等式的解集的方法:
不等号是大于时,射线向 画,不等号是小于时,射线向 画.有等号时画 点,无等号时画 .
空心圆圈
右
求不等式的解集的过程
所有的解
未知数的值
无数
左
实心
·导学建议·
此活动环节,要让学生充分发表意见,并通过计算、动手验证、动脑思考,初步体会不等式解的意义以及不等式解与方程解的不同之处.
用不等式表示数量关系
例1 下列说法中正确的是 ( )
A.x=1是不等式-2x<1的解
B.x=-1是不等式-2x<1的解
C.x=-是不等式-2x<1的解
D.不等式-2x<1的解集是x=1
A
·导学建议·
通过题型一的学习,让学生明白不等式的解集包括了不等式的每个解,解集中任何一个数都是不等式的一个解.
变式训练 用不等式表示下列语句.
(1)m的与n的的差是正数;(2)y与1的和小于y的;(3)y的40%与5的差小于0.
读懂数或字母间的数量关系→找准不等关系→列不等式.
解:(1)m-n>0;(2)y+1
例2 对于不等式x+3>6,完成以下问题:
(1)x=1,x=2,x=3,x=4,x=5,x=6,哪些是x+3>6的解 哪些不是
(2)不等式x+3>6的解集是什么 并在数轴上表示出来.
解:(1)x=4,x=5,x=6是不等式的解,x=1,x=2,x=3不是.
(2)x>3.在数轴上表示略.
方法归纳交流 1.验证一个未知数的值是不是不等式的解的方法:将未知数的值代入到不等式中,使不等式成立,则未知数的值即是不等式的解.否则不是.
2.在数轴上表示不等式的解集时,空心圆圈表示解集不包括这个点,注意画线的方向问题.
1.下列各式中,不是不等式的是 ( )
A.2x≠1 B.-5<1
C.4x-1<6 D.y=x-4
D
2.用含x的不等式表示下列数轴所表示的解集:
(1)
(2)
(3)
(4)
解:(1)表示的解集为x>-1.
(2)表示的解集为x≥-2.
(3)表示的解集为x≤-.
(4)表示的解集为x≤-2.5.
1.如图,数轴上所示的解集用不等式表示正确的是 ( )
A.x>-2 B.x≥-2 C.x<-2 D.x≤-2
C
2.给出下列四个式子:①4<7;②a<3;③a≠0;④a>b.其中是不等式的是 ( )
A.②③ B.①②③
C.②③④ D.①②③④
D
3.请写出一个关于x的不等式,使-1,2都是它的解:
.
x-1<2(答案不唯一)
4.用不等式表示下列数量关系:
(1)m与3的和小于n;
(2)x与12的差比y的3倍大;
(3)a与b的乘积是正数.
解:(1)m+3
5.下列各数中:-8,-2.5,0,1,,2,-,4使不等式2x>2成立的数有 ( )
A.5个 B.4个 C.3个 D.2个
C
6.直接写出下列不等式的解集:
(1)x-3>0的解集是 ;
(2)2x<12的解集是 ;
(3)x+2<4的解集是 .
x<2
x<6
x>3
7.用不等式表示如图所示的天平的两边所给的量之间的关系.
解:40>10+2x.
8.某班去某博物馆参观,花了220元租了一辆客车,设这个班的人数为x人.
(1)如果每人交8元租车费后,还有剩余,请写出x应满足的不等式.
(2)如果每人交7元的租车费,结果还不够,这时x应满足的不等式是什么呢
解:(1)8x>220;(2)7x<220.
同课章节目录
