6.1.1 函数的平均变化率 课件(19页PPT)
文档属性
| 名称 | 6.1.1 函数的平均变化率 课件(19页PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-15 16:27:36 | ||
图片预览




文档简介
第六章 导数及其应用
6.1.1 函数的平均变化率
人教B版(2019)选择性必修第三册
1.理解函数平均变化率的概念,会求函数的平均变化率.
2.理解函数平均变化率的几何意义和物理意义.
3.会求函数在某一点附近的平均变化率,并能用平均变化率解释一些实际问题.
世界上的变化无处不在,人们经常关心变化的快慢问题.如何刻画事物变化的快慢呢?
B(25,16.4)
1
A(1,3.6)
16.4
3.6
28.8
O
25
27
t (d)
T(oC)
C(27,28.8)
气温曲线
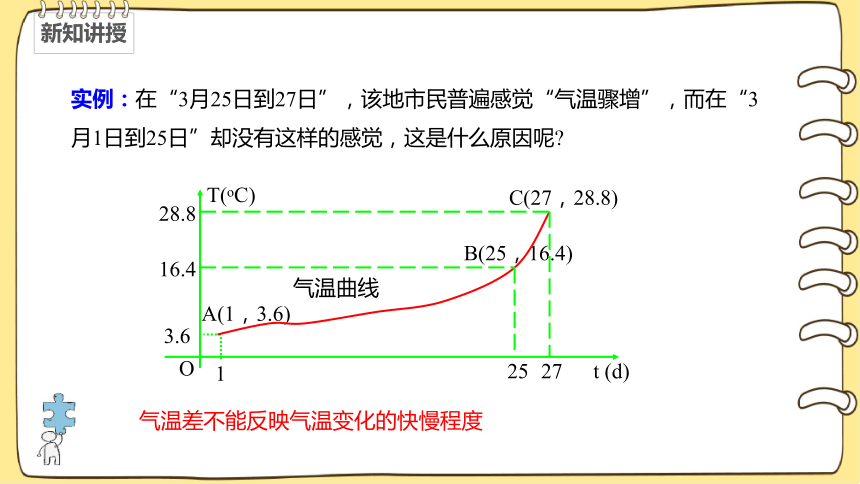
实例:在“3月25日到27日”,该地市民普遍感觉“气温骤增”,而在“3月1日到25日”却没有这样的感觉,这是什么原因呢?
气温差不能反映气温变化的快慢程度
B(25,16.4)
1
A(1,3.6)
16.4
3.6
28.8
O
25
27
t (d)
T(oC)
C(27,28.8)
气温曲线
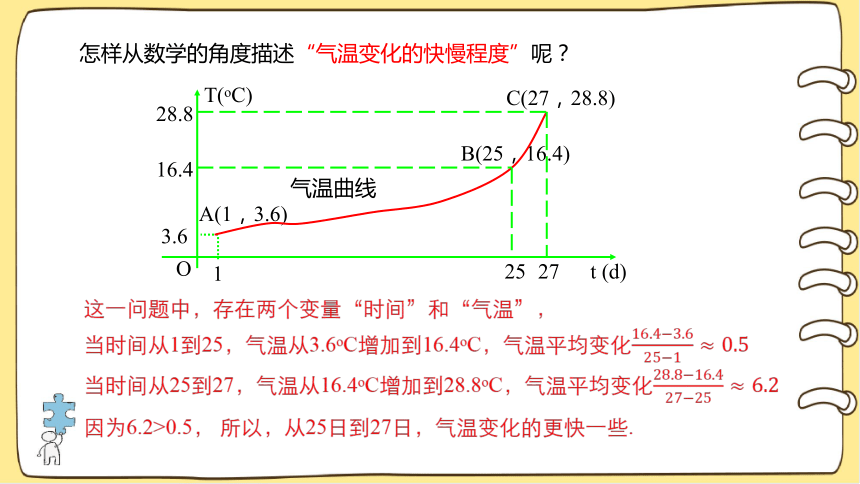
怎样从数学的角度描述“气温变化的快慢程度”呢?
这一问题中,存在两个变量“时间”和“气温”,
当时间从1到25,气温从3.6oC增加到16.4oC,气温平均变化16.4?3.625?1≈0.5
当时间从25到27,气温从16.4oC增加到28.8oC,气温平均变化28.8?16.427?25≈6.2
因为6.2>0.5, 所以,从25日到27日,气温变化的更快一些.
?
一般地,若函数y=f(x)的定义域为D,且x1,x2∈D,x1≠x2,y1=f(x1),y2=f(x2),则称Δx=x2-x1为自变量的改变量;
称Δy=y2-y1(或Δf=f(x2)-f(x1))为相应的因变量的改变量;
称Δ????Δ????=????2?????1????2?????1或Δ????Δ????=????(????2)?????(????1)????2?????1为函数y=f(x)在以x1,x2为端点的闭区间上的平均变化率.
?
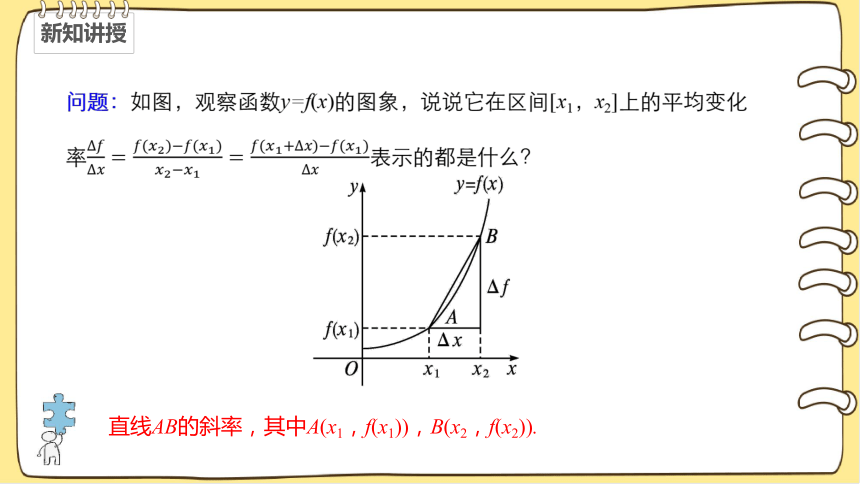
问题:如图,观察函数y=f(x)的图象,说说它在区间[x1,x2]上的平均变化率Δ????Δ????=????(????2)?????(????1)????2?????1=????(????1+Δ????)?????(????1)Δ????表示的都是什么?
?
直线AB的斜率,其中A(x1,f(x1)),B(x2,f(x2)).
函数平均变化率的几何意义:
如图所示,函数f(x)在区间[x1,x2]上的平均变化率,就是直线AB的斜率,其中A(x1,f(x1)),B(x2,f(x2)). 事实上,
讨论:在平均变化率中, Δx, Δy, ΔyΔx是否可以等于0?当平均变化率等于0时,是否说明函数在该区间上一定为常数?
?
Δx可以为正数,也可以为负数,但Δx不可以为0,Δy可以为0.
当平均变化率ΔyΔx等于0时,并不说明函数在该区间上一定为常数.
例如函数f(x)=x2在区间[-2,2]的平均变化率是0,但它不是常数函数.
?
例1 已知函数f(x)=2x2-1的图象上一点(1,1)及邻近一点(1+Δx,1+Δy),则ΔyΔx=( )
A.4 B.4x C.4+2Δx D.4+2(Δx)2
?
解析:∵Δy=f(1+Δx)-f(1)=[2(1+Δx)2-1]-1=2Δx2+4Δx,
∴????y????x=2Δx+4.
?
C
例2 已知函数f(x)=x+1x,分别计算f(x)在自变量x从1变到2和从3变到5时的平均变化率,并判断在哪个区间上函数值变化得较快.
?
?
解:自变量x从1变到2时,函数f(x)的平均变化率为f2?f12?1=2+12?1+11=12;
自变量x从3变到5时,函数f(x)的平均变化率为f5?f35?3=5+15?3+132=1415.
因为12<1415,所以函数f(x)=x+1x在自变量x从3变到5时函数值变化得较快.
?
方法归纳
求平均变化率的主要步骤
第一步,求自变量的增量Δx=x2-x1;
第二步,求函数值的增量Δy=f(x2)-f(x1);
第三步,求平均变化率Δ????Δ????=????????2?????????1????2?????1.
?
当不断放大时,曲线在点P附近的图象逼近一条确定的直线,即在很小的范围内,曲线可以看作直线,这就是以直代曲的思想.
看图说话:如图,我们把一条曲线上的任意一点P附近的图象不断放大,观察有何现象出现?
例3 已知函数f(x)的部分图象如图所示.若把曲线AB近似地看成线段,则图中阴影部分的面积近似为 .
32
?
解析:若把曲线AB近似看成线段,则阴影部分的面积近似为直角三角形的面积S=12×1×3=32.
?
从物理学中我们知道,平均速度可以描述物体在一段时间内运动的快慢,如果物体运动的位移x m与时间t s的关系为x=h(t),则物体在[t1,t2](t1?????2??(????1)????2?????1 (m/s).
这就是说,物体在某段时间内的平均速度等于x=h(t)在该段时间内的平均变化率.
?
例4 质点运动规律s=12gt2,则在时间区间(3,3+Δt)内的平均速度等于________.(g=10 m/s2)
?
解析:Δs=12g×(3+Δt)2-12g×32=12×10×[6Δt+(Δt)2]=30Δt+5(Δt)2,
v=ΔsΔt=30+5Δt.
?
30+5Δt
1.一物体的运动方程是????=3+????2,则在一小段时间[2,2.1]内相应的平均速度为( )
A.0.41 B.3 C.4 D.4.1
?
D
2.如图,函数y=f(x)在A,B两点间的平均变化率是( )
A.1 B.-1 C.2 D.-2
B
3.一物体的运动函数是s(t)=3+2t,则在[2,2.1]这段时间内的平均速度 .
4.函数f(x)=x2-1在区间[1,m]上的平均变化率为3,则实数m的值为 .?
5.如图所示,函数y=f(x)在[x1,x2],[x2,x3],[x3,x4]这几个区间内,平均变化率最大的一个区间是_____________.
2
2
[x3,x4]
函数的平均变化率
定义
几何背景
物理背景
割线斜率
平均速度
6.1.1 函数的平均变化率
人教B版(2019)选择性必修第三册
1.理解函数平均变化率的概念,会求函数的平均变化率.
2.理解函数平均变化率的几何意义和物理意义.
3.会求函数在某一点附近的平均变化率,并能用平均变化率解释一些实际问题.
世界上的变化无处不在,人们经常关心变化的快慢问题.如何刻画事物变化的快慢呢?
B(25,16.4)
1
A(1,3.6)
16.4
3.6
28.8
O
25
27
t (d)
T(oC)
C(27,28.8)
气温曲线
实例:在“3月25日到27日”,该地市民普遍感觉“气温骤增”,而在“3月1日到25日”却没有这样的感觉,这是什么原因呢?
气温差不能反映气温变化的快慢程度
B(25,16.4)
1
A(1,3.6)
16.4
3.6
28.8
O
25
27
t (d)
T(oC)
C(27,28.8)
气温曲线
怎样从数学的角度描述“气温变化的快慢程度”呢?
这一问题中,存在两个变量“时间”和“气温”,
当时间从1到25,气温从3.6oC增加到16.4oC,气温平均变化16.4?3.625?1≈0.5
当时间从25到27,气温从16.4oC增加到28.8oC,气温平均变化28.8?16.427?25≈6.2
因为6.2>0.5, 所以,从25日到27日,气温变化的更快一些.
?
一般地,若函数y=f(x)的定义域为D,且x1,x2∈D,x1≠x2,y1=f(x1),y2=f(x2),则称Δx=x2-x1为自变量的改变量;
称Δy=y2-y1(或Δf=f(x2)-f(x1))为相应的因变量的改变量;
称Δ????Δ????=????2?????1????2?????1或Δ????Δ????=????(????2)?????(????1)????2?????1为函数y=f(x)在以x1,x2为端点的闭区间上的平均变化率.
?
问题:如图,观察函数y=f(x)的图象,说说它在区间[x1,x2]上的平均变化率Δ????Δ????=????(????2)?????(????1)????2?????1=????(????1+Δ????)?????(????1)Δ????表示的都是什么?
?
直线AB的斜率,其中A(x1,f(x1)),B(x2,f(x2)).
函数平均变化率的几何意义:
如图所示,函数f(x)在区间[x1,x2]上的平均变化率,就是直线AB的斜率,其中A(x1,f(x1)),B(x2,f(x2)). 事实上,
讨论:在平均变化率中, Δx, Δy, ΔyΔx是否可以等于0?当平均变化率等于0时,是否说明函数在该区间上一定为常数?
?
Δx可以为正数,也可以为负数,但Δx不可以为0,Δy可以为0.
当平均变化率ΔyΔx等于0时,并不说明函数在该区间上一定为常数.
例如函数f(x)=x2在区间[-2,2]的平均变化率是0,但它不是常数函数.
?
例1 已知函数f(x)=2x2-1的图象上一点(1,1)及邻近一点(1+Δx,1+Δy),则ΔyΔx=( )
A.4 B.4x C.4+2Δx D.4+2(Δx)2
?
解析:∵Δy=f(1+Δx)-f(1)=[2(1+Δx)2-1]-1=2Δx2+4Δx,
∴????y????x=2Δx+4.
?
C
例2 已知函数f(x)=x+1x,分别计算f(x)在自变量x从1变到2和从3变到5时的平均变化率,并判断在哪个区间上函数值变化得较快.
?
?
解:自变量x从1变到2时,函数f(x)的平均变化率为f2?f12?1=2+12?1+11=12;
自变量x从3变到5时,函数f(x)的平均变化率为f5?f35?3=5+15?3+132=1415.
因为12<1415,所以函数f(x)=x+1x在自变量x从3变到5时函数值变化得较快.
?
方法归纳
求平均变化率的主要步骤
第一步,求自变量的增量Δx=x2-x1;
第二步,求函数值的增量Δy=f(x2)-f(x1);
第三步,求平均变化率Δ????Δ????=????????2?????????1????2?????1.
?
当不断放大时,曲线在点P附近的图象逼近一条确定的直线,即在很小的范围内,曲线可以看作直线,这就是以直代曲的思想.
看图说话:如图,我们把一条曲线上的任意一点P附近的图象不断放大,观察有何现象出现?
例3 已知函数f(x)的部分图象如图所示.若把曲线AB近似地看成线段,则图中阴影部分的面积近似为 .
32
?
解析:若把曲线AB近似看成线段,则阴影部分的面积近似为直角三角形的面积S=12×1×3=32.
?
从物理学中我们知道,平均速度可以描述物体在一段时间内运动的快慢,如果物体运动的位移x m与时间t s的关系为x=h(t),则物体在[t1,t2](t1
这就是说,物体在某段时间内的平均速度等于x=h(t)在该段时间内的平均变化率.
?
例4 质点运动规律s=12gt2,则在时间区间(3,3+Δt)内的平均速度等于________.(g=10 m/s2)
?
解析:Δs=12g×(3+Δt)2-12g×32=12×10×[6Δt+(Δt)2]=30Δt+5(Δt)2,
v=ΔsΔt=30+5Δt.
?
30+5Δt
1.一物体的运动方程是????=3+????2,则在一小段时间[2,2.1]内相应的平均速度为( )
A.0.41 B.3 C.4 D.4.1
?
D
2.如图,函数y=f(x)在A,B两点间的平均变化率是( )
A.1 B.-1 C.2 D.-2
B
3.一物体的运动函数是s(t)=3+2t,则在[2,2.1]这段时间内的平均速度 .
4.函数f(x)=x2-1在区间[1,m]上的平均变化率为3,则实数m的值为 .?
5.如图所示,函数y=f(x)在[x1,x2],[x2,x3],[x3,x4]这几个区间内,平均变化率最大的一个区间是_____________.
2
2
[x3,x4]
函数的平均变化率
定义
几何背景
物理背景
割线斜率
平均速度
