6.1.2 课时1 瞬时变化率与导数 课件(20张PPT)
文档属性
| 名称 | 6.1.2 课时1 瞬时变化率与导数 课件(20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-15 16:31:13 | ||
图片预览








文档简介
6.1.2 课时1
瞬时变化率与导数
人教B版(2019)选择性必修第三册
1.理解瞬时变化率、导数的概念.
2.理解导数的几何意义.
3.会用导数的定义及几何意义求曲线在某点处的切线方程.
上节已经学习了函数的平均变化率和物体运动的平均速度的概念,二者有何关系?
物体做变速运动时,设物体走过的路程????=????(????),
则从????0到????0+?????的过程中,物体运动的平均速度就是函数????=????(????)在[????0,????0+?????]上的平均变化率.
?
阅读下列实例,回答问题:
实例1:一个小球从高空自由下落,其下落的高度h(单位:m)与时间t(单位:s)的函数关系为 ,其中,g为重力加速度(g取9. 8 m/s2).估算小球在t=5 s这个时刻的瞬时速度.
分析:当时间t从t0变到t1时,根据平均速度公式 ,
可以求出从5 s到6 s这段时间内小球的平均速度
有时用它来近似表示小球在t=5s这个时刻的瞬时速度.
为了提高精度,可以缩短时间间隔,如求出5s到5.1s这段时间内的平均速度
用它来近似表示小球在t=5s这个时刻的瞬时速度,这样更接近实际情况.
如果时间间隔进一步缩短,那么可以想象,平均速度就更接近小球在t=5s这个时刻的瞬时速度.
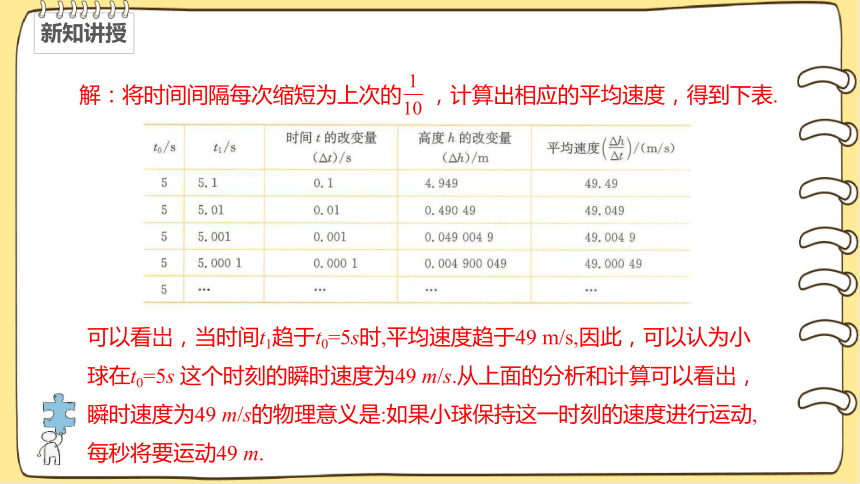
解:将时间间隔每次缩短为上次的 ,计算出相应的平均速度,得到下表.
可以看岀,当时间t1趋于t0=5s时,平均速度趋于49 m/s,因此,可以认为小球在t0=5s 这个时刻的瞬时速度为49 m/s.从上面的分析和计算可以看岀,瞬时速度为49 m/s的物理意义是:如果小球保持这一时刻的速度进行运动,每秒将要运动49 m.
可以看出,当x1趋于x0=2 m时,平均线密度趋于0.707 kg/m.
实例2:如图, 一根质量分布不均匀的合金棒,长为10 m.设x(单位:m)表示OX这段棒的长,y(单位:kg)表示OX这段棒的质量,它们满足以下函数关系:
估计该合金棒在x=2 m处的线密度(物理学的“线密度”定义为单位长度的质量).
解:由 ,可以计算出相应的平均线密度,得到下表.
从上面的分析和计算可以看出,线密度为0.707 kg/m的物理意义是:如果有1 m长的这种线密度的质量均匀的合金棒,其质量将为0. 707 kg.
与实例1类似,同学们也可以动手计算当x1从“左侧”趋近于x0=2 m时的平均线密 度,会发现也趋于0.707 kg/m.
据此,可以认为合金棒在x0=2 m处的线密度约为0.707 kg/m.
实例1和实例2都是通过减小自变量的改变量(为计算方便选取 ,也可以选取 等), 用平均变化率“逼近”瞬时变化率.
1.函数的瞬时变化率
一般地,设函数????=????(????)在????0附近有定义,自变量在????=????0处的改变量为Δ????,当Δ????无限接近于0时,若平均变化率
??????????=????????0+??????????????0?????,
无限接近于一个常数k,那么称常数k为函数????(????)在????=????0处的瞬时变化率.
?
记作:当Δ????→0时,????????0+??????????????0?????→????
?
2.导数
函数????(????)在????=????0处的瞬时变化率为k,也称????(????)在x0处可导,并称k为????(????)在????=????0处的导数,记作????′(????0)=????.
?
记作:lim?????→0??????(????0+?????)?–??????(????0)?????=????,即f ?(x0) =lim?????→0??????(????0+?????)?–??????(????0)????? .
?
还可以说:当Δx→0时,函数的平均变化率的极限等于函数在x0处的瞬时变化率????.
?
讨论:平均变化率与瞬时变化率有什么关系?
区别:平均变化率刻画函数值在区间[????1,????2]上变化的快慢,瞬时变化率刻画函数值在????0点处变化的快慢;
联系:当Δ????趋于0时,平均变化率Δ????Δ????趋于一个常数,这个常数即为函数在
????0处的瞬时变化率,它是一个固定值.
?
“Δ????趋于0”的含义:?Δ????趋于0的距离要多近有多近,即Δ?????0可以小于给定的任意小的正数,且始终Δ????≠0.
?
例1 某物体的运动路程s(单位:m)与时间t(单位:s)的关系可用函数s(t)=????2+????+1表示,求物体在t=1s时的瞬时速度.
?
解: Δ????Δ????=????1+Δ?????????1Δ????=1+Δ????2+1+Δ????+1?12+1+1Δ????=3+Δ????,
当Δ????趋于0时,Δ????Δ????趋于3,即物体在t=1s时的瞬时速度为3 m/s.
?
变式1:某物体的运动路程s(单位:m)与时间t(单位:s)的关系可用函数s(t)=t2+t+1表示,试求物体的初速度.
解:求物体的初速度,即求物体在t=0时的瞬时速度,
即物体的初速度为1 m/s.
解:设物体在t0时刻的瞬时速度为9 m/s.
则2t0+1=9,∴t0=4.
则物体在4 s时的瞬时速度为9 m/s.
变式2:某物体的运动路程s(单位:m)与时间t(单位:s)的关系可用函数s(t)=t2+t+1表示,试问物体在哪一时刻的瞬时速度为9 m/s.
求函数????????在点????=????????处的瞬时变化率的步骤:
(1)求Δ????=????????0+Δ?????????????0;
(2)计算Δ????Δ????,并化简,直到当Δ????=0时有意义为止;
(3)将Δ????=0代入化简后的即得瞬时变化率.
?
方法归纳
解:f'(1)=4表示该工人上班后工作1h的时候,其生产速度(即工作效率)为4 kg/h.也就是说,如果保持这一生产速度,那么他每时可以生产4 kg的食品.
例2 一名食品加工厂的工人上班后开始连续工作,生产的食品量y(单位:kg)与其工作时间x(单位:h)的函数关系为y=f(x).假设函数y=f(x)在x=l和x=3处的导数分别为f'(1)=4和f'(3) =3.5,试解释它们的实际意义.
f'(3) =3.5表示该工人上班后工作3 h的时候,其生产速度为3.5 kg/h.也就是说,如果保持这一生产速度,那么他每时可以生产3. 5 kg的食品.
例3 求函数y=f(x)=x-1????在x=-1处的导数.
?
解:∵Δy=f(-1+Δx)-f(-1)=-1+Δx-1?1+Δ????-0=?2Δ????+(Δ????)2?1+Δ????,
∴Δ????Δ????=?2Δ????+(Δ????)2(?1+Δ????)Δ????=?2+Δ?????1+Δ????,
故函数在x=-1处的导数f'(-1)=limΔ????→0Δ????Δ????=limΔ????→0?2+Δ?????1+Δ????=2.
?
1.物体运动函数为s(t)=3t2(位移单位:m,时间单位:s),若当Δt趋于0时,
趋于18 m/s,则下列说法中正确的是( )
A.18 m/s是物体从0 s到3 s这段时间内的平均速度
B.18 m/s是物体从3 s到(3+Δt)s这段时间内的速度
C.18 m/s是物体在3 s这一时刻的瞬时速度
D.18 m/s是物体从3 s到(3+Δt)s这段时间内的平均速度
C
2.某运动物体的位移s(单位:米)关于时间t(单位:秒)的函数关系式为s=2t+1,则该物体在t=1秒时的瞬时速度为( )
A.1米/秒 B.2米/秒
C.3米/秒 D.4米/秒
3.已知物体运动的速度与时间之间的关系是v(t)=t2+2t+2,则在时间间隔[1,1+Δt]内的平均加速度是 ,在t=1时的瞬时加速度是 .?
4.已知函数f(x)在x=x0处的导数为2,则limΔ????→0????(????0+Δ????)?????(????0)2Δ????= .
?
B
4+Δt
4
1
1. 什么是函数的瞬时变化率?它和平均变化率有什么联系?
2. 导数的概念是什么?如何求解函数在某处的导数?
回顾:结合本节课所学,回答下列问题?
瞬时变化率与导数
人教B版(2019)选择性必修第三册
1.理解瞬时变化率、导数的概念.
2.理解导数的几何意义.
3.会用导数的定义及几何意义求曲线在某点处的切线方程.
上节已经学习了函数的平均变化率和物体运动的平均速度的概念,二者有何关系?
物体做变速运动时,设物体走过的路程????=????(????),
则从????0到????0+?????的过程中,物体运动的平均速度就是函数????=????(????)在[????0,????0+?????]上的平均变化率.
?
阅读下列实例,回答问题:
实例1:一个小球从高空自由下落,其下落的高度h(单位:m)与时间t(单位:s)的函数关系为 ,其中,g为重力加速度(g取9. 8 m/s2).估算小球在t=5 s这个时刻的瞬时速度.
分析:当时间t从t0变到t1时,根据平均速度公式 ,
可以求出从5 s到6 s这段时间内小球的平均速度
有时用它来近似表示小球在t=5s这个时刻的瞬时速度.
为了提高精度,可以缩短时间间隔,如求出5s到5.1s这段时间内的平均速度
用它来近似表示小球在t=5s这个时刻的瞬时速度,这样更接近实际情况.
如果时间间隔进一步缩短,那么可以想象,平均速度就更接近小球在t=5s这个时刻的瞬时速度.
解:将时间间隔每次缩短为上次的 ,计算出相应的平均速度,得到下表.
可以看岀,当时间t1趋于t0=5s时,平均速度趋于49 m/s,因此,可以认为小球在t0=5s 这个时刻的瞬时速度为49 m/s.从上面的分析和计算可以看岀,瞬时速度为49 m/s的物理意义是:如果小球保持这一时刻的速度进行运动,每秒将要运动49 m.
可以看出,当x1趋于x0=2 m时,平均线密度趋于0.707 kg/m.
实例2:如图, 一根质量分布不均匀的合金棒,长为10 m.设x(单位:m)表示OX这段棒的长,y(单位:kg)表示OX这段棒的质量,它们满足以下函数关系:
估计该合金棒在x=2 m处的线密度(物理学的“线密度”定义为单位长度的质量).
解:由 ,可以计算出相应的平均线密度,得到下表.
从上面的分析和计算可以看出,线密度为0.707 kg/m的物理意义是:如果有1 m长的这种线密度的质量均匀的合金棒,其质量将为0. 707 kg.
与实例1类似,同学们也可以动手计算当x1从“左侧”趋近于x0=2 m时的平均线密 度,会发现也趋于0.707 kg/m.
据此,可以认为合金棒在x0=2 m处的线密度约为0.707 kg/m.
实例1和实例2都是通过减小自变量的改变量(为计算方便选取 ,也可以选取 等), 用平均变化率“逼近”瞬时变化率.
1.函数的瞬时变化率
一般地,设函数????=????(????)在????0附近有定义,自变量在????=????0处的改变量为Δ????,当Δ????无限接近于0时,若平均变化率
??????????=????????0+??????????????0?????,
无限接近于一个常数k,那么称常数k为函数????(????)在????=????0处的瞬时变化率.
?
记作:当Δ????→0时,????????0+??????????????0?????→????
?
2.导数
函数????(????)在????=????0处的瞬时变化率为k,也称????(????)在x0处可导,并称k为????(????)在????=????0处的导数,记作????′(????0)=????.
?
记作:lim?????→0??????(????0+?????)?–??????(????0)?????=????,即f ?(x0) =lim?????→0??????(????0+?????)?–??????(????0)????? .
?
还可以说:当Δx→0时,函数的平均变化率的极限等于函数在x0处的瞬时变化率????.
?
讨论:平均变化率与瞬时变化率有什么关系?
区别:平均变化率刻画函数值在区间[????1,????2]上变化的快慢,瞬时变化率刻画函数值在????0点处变化的快慢;
联系:当Δ????趋于0时,平均变化率Δ????Δ????趋于一个常数,这个常数即为函数在
????0处的瞬时变化率,它是一个固定值.
?
“Δ????趋于0”的含义:?Δ????趋于0的距离要多近有多近,即Δ?????0可以小于给定的任意小的正数,且始终Δ????≠0.
?
例1 某物体的运动路程s(单位:m)与时间t(单位:s)的关系可用函数s(t)=????2+????+1表示,求物体在t=1s时的瞬时速度.
?
解: Δ????Δ????=????1+Δ?????????1Δ????=1+Δ????2+1+Δ????+1?12+1+1Δ????=3+Δ????,
当Δ????趋于0时,Δ????Δ????趋于3,即物体在t=1s时的瞬时速度为3 m/s.
?
变式1:某物体的运动路程s(单位:m)与时间t(单位:s)的关系可用函数s(t)=t2+t+1表示,试求物体的初速度.
解:求物体的初速度,即求物体在t=0时的瞬时速度,
即物体的初速度为1 m/s.
解:设物体在t0时刻的瞬时速度为9 m/s.
则2t0+1=9,∴t0=4.
则物体在4 s时的瞬时速度为9 m/s.
变式2:某物体的运动路程s(单位:m)与时间t(单位:s)的关系可用函数s(t)=t2+t+1表示,试问物体在哪一时刻的瞬时速度为9 m/s.
求函数????????在点????=????????处的瞬时变化率的步骤:
(1)求Δ????=????????0+Δ?????????????0;
(2)计算Δ????Δ????,并化简,直到当Δ????=0时有意义为止;
(3)将Δ????=0代入化简后的即得瞬时变化率.
?
方法归纳
解:f'(1)=4表示该工人上班后工作1h的时候,其生产速度(即工作效率)为4 kg/h.也就是说,如果保持这一生产速度,那么他每时可以生产4 kg的食品.
例2 一名食品加工厂的工人上班后开始连续工作,生产的食品量y(单位:kg)与其工作时间x(单位:h)的函数关系为y=f(x).假设函数y=f(x)在x=l和x=3处的导数分别为f'(1)=4和f'(3) =3.5,试解释它们的实际意义.
f'(3) =3.5表示该工人上班后工作3 h的时候,其生产速度为3.5 kg/h.也就是说,如果保持这一生产速度,那么他每时可以生产3. 5 kg的食品.
例3 求函数y=f(x)=x-1????在x=-1处的导数.
?
解:∵Δy=f(-1+Δx)-f(-1)=-1+Δx-1?1+Δ????-0=?2Δ????+(Δ????)2?1+Δ????,
∴Δ????Δ????=?2Δ????+(Δ????)2(?1+Δ????)Δ????=?2+Δ?????1+Δ????,
故函数在x=-1处的导数f'(-1)=limΔ????→0Δ????Δ????=limΔ????→0?2+Δ?????1+Δ????=2.
?
1.物体运动函数为s(t)=3t2(位移单位:m,时间单位:s),若当Δt趋于0时,
趋于18 m/s,则下列说法中正确的是( )
A.18 m/s是物体从0 s到3 s这段时间内的平均速度
B.18 m/s是物体从3 s到(3+Δt)s这段时间内的速度
C.18 m/s是物体在3 s这一时刻的瞬时速度
D.18 m/s是物体从3 s到(3+Δt)s这段时间内的平均速度
C
2.某运动物体的位移s(单位:米)关于时间t(单位:秒)的函数关系式为s=2t+1,则该物体在t=1秒时的瞬时速度为( )
A.1米/秒 B.2米/秒
C.3米/秒 D.4米/秒
3.已知物体运动的速度与时间之间的关系是v(t)=t2+2t+2,则在时间间隔[1,1+Δt]内的平均加速度是 ,在t=1时的瞬时加速度是 .?
4.已知函数f(x)在x=x0处的导数为2,则limΔ????→0????(????0+Δ????)?????(????0)2Δ????= .
?
B
4+Δt
4
1
1. 什么是函数的瞬时变化率?它和平均变化率有什么联系?
2. 导数的概念是什么?如何求解函数在某处的导数?
回顾:结合本节课所学,回答下列问题?
