6.1.2 课时2 导数的几何意义 课件(21张PPT)
文档属性
| 名称 | 6.1.2 课时2 导数的几何意义 课件(21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1014.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-15 00:00:00 | ||
图片预览







文档简介
6.1.2 课时2
导数的几何意义
人教B版(2019)选择性必修第三册
1.掌握导数的几何意义,并能求切线斜率、切线方程等.
求函数 y=f (x)在 x=x0 处导数的步骤
问题:(1)函数y=f(x)在[x0,x0+Δx]的平均变化率为 ,你能说出它的几何意义吗?
表示过A(x0,f(x0))和B(x0+Δx,f(x0+Δx))两点的直线的斜率,这条直线称为曲线y=f(x)在点A处的一条割线.
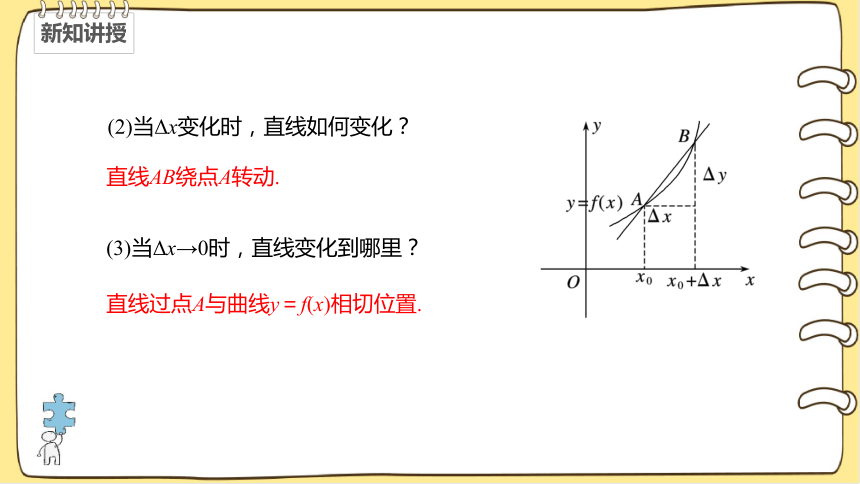
(2)当Δx变化时,直线如何变化?
直线AB绕点A转动.
(3)当Δx→0时,直线变化到哪里?
直线过点A与曲线y=f(x)相切位置.
函数y=f(x)在x0处的导数f′(x0),是曲线y=f(x)在点(x0,f(x0))处的切线的斜率,函数y=f(x)在x0处切线的斜率反映了导数的几何意义.
思考1:如何求曲线f(x)在点(x0,f(x0))处的切线方程?
根据导数的几何意义,求出函数y=f(x)在点(x0,f(x0))处的导数,即曲线在该点处的切线的斜率,再由直线方程的点斜式求出切线方程.
思考2:曲线f(x)在点(x0,f(x0))处的切线与曲线过点(x0,y0)的切线有什么不同?
曲线f(x)在点(x0,f(x0))处的切线,点(x0,f(x0))一定是切点,只要求出k=f'(x0),利用点斜式写出切线方程即可;
而曲线f(x)过某点(x0,y0)的切线,给出的点(x0,y0)不一定在曲线上,即使在曲线上也不一定是切点.
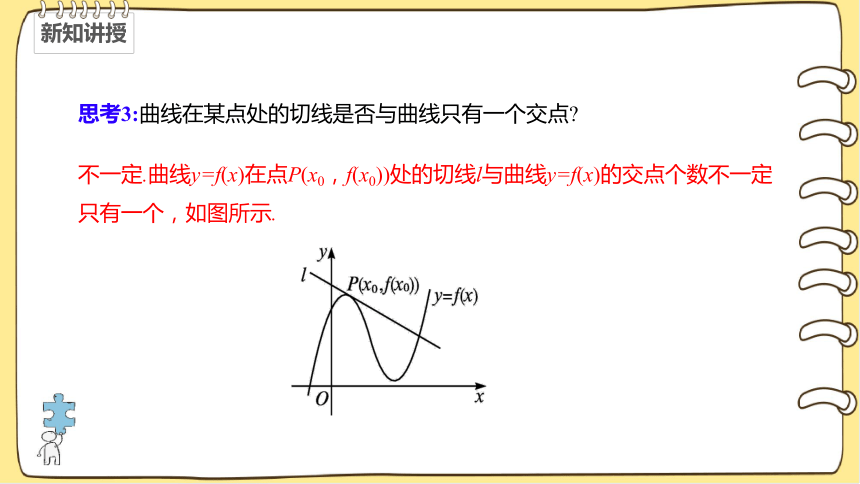
思考3:曲线在某点处的切线是否与曲线只有一个交点?
不一定.曲线y=f(x)在点P(x0,f(x0))处的切线l与曲线y=f(x)的交点个数不一定只有一个,如图所示.
解:∵P(2,4)在曲线y=13x3+43上,
∴曲线在点P(2,4)处切线的斜率为
k=limΔ????→013(2+Δ????)3+43?13×23+43Δ????=limΔ????→04+2Δ????+13(Δ????)2=4.
∴曲线在点P(2,4)处的切线方程为y-4=4(x-2),
即4x-y-4=0.
?
例1 已知曲线y=13x3+43,求曲线在点P(2,4)处的切线方程.
?
变式:已知曲线y=13x3+43,求曲线过点P(2,4)处的切线方程.
?
解:设曲线y=13x3+43与过点P(2,4)的切线相切于点A????0,13????03+43,
则切线的斜率为k=limΔ????→013(????0+Δ????)3?13????03Δ????=????02,
∴切线方程为y-13????03+43=????02(x-x0),即y=????02·x-23????03+43.
∵点P(2,4)在切线上,∴4=2????02-23????03+43,即????03-3????02+4=0.
?
∴????03+????02-4????02+4=0,
∴????02(x0+1)-4(x0+1)(x0-1)=0,
∴(x0+1)(x0-2)2=0,
解得x0=-1或x0=2.
故所求的切线方程为x-y+2=0或4x-y-4=0.
?
变式:已知曲线y=13x3+43,求曲线过点P(2,4)处的切线方程.
?
1.求曲线在某点处的切线方程时,该点就是切点,因此可直接求出切线斜率,写出切线方程.
2.求过曲线上某点的切线方程时,要注意该点不一定是切点.因此,在解题时要先设出切点,再求出切线斜率,根据切点与斜率写出切线方程,最后将该点的坐标代入.在解题过程中不必考虑该点是否为切点.
归纳总结
例2 已知函数y1=f(x)=x2-1在x=x0处的切线与函数y2=g(x)=1-x3在x=x0处的切线互相平行,求x0的值.
方法总结
根据切线斜率求切点坐标的步骤
(1)设切点坐标(x0,y0).
(2)求导函数f'(x).
(3)求切线的斜率f'(x0).
(4)由斜率间的关系列出关于x0的方程,解方程求x0.
(5)点(x0,y0)在曲线f(x)上,将(x0,y0)代入求y0,得切点坐标.
借助曲线的切线,我们还可以从几何上来理解瞬时变化率的实际意义,并可以利用某一点的导数来估计这一点附近的函数值,具体过程如下.
如果函数????=????(????)在????0处的导数为????′(????0),且在????0处自变量的改变量为?????,对应的函数值改变量为
?????=????????0+??????????(????0),
则
????????0+?????=????????0+?????
?
此时曲线????=????(????)在????0处的切线l的斜率为????′(????0),因此
AC=?????,CD=????′(????0) ?????.
又因为BC=?y,可以看出,当?????很小时,?????可用????′(????0) ?????来近似表示,即
?y≈????′(????0)??????,
所以 ????????0+?????≈????????0+????′(????0)??????.
?
?????
?
本质上是用????=????0处的切线代替了????=????0附近的曲线????=????(????),使用了“以直代曲”的方法.
?
例3 已知f(x)=x2+1,利用f(1)=2,f'(1)=2,Δx=0.04,则f(1.04)的近似值为 .
2.08
解析:设x=x0+Δx,Δx=x-x0,
则有f(x)≈f(x0)+f'(x0)(x-x0),
所以f(1.04)≈f(1)+0.04f'(1)=2+0.04×2=2.08.
1.已知函数f(x)=?1????,则曲线y=f (x)在(1,-1)处的切线方程是( )
A.x-y-2=0 B.2x-2y+3=0
C.x+y=0 D.x-y=0
?
A
2.函数y=f(x)=2x2+4x在x=3处的导数为 .
3.曲线y=14x2在点Q(2,1)处的切线方程为 .
4.已知曲线y=f(x)=2x2+4x在点P处的切线斜率为16,则P点坐标为________.
?
16
x-y-1=0
(3,30)
根据今天所学,回答下列问题:
1.如何求函数在某点处的切线的方程?
2.如何根据切线斜率求切点坐标?
导数的几何意义
人教B版(2019)选择性必修第三册
1.掌握导数的几何意义,并能求切线斜率、切线方程等.
求函数 y=f (x)在 x=x0 处导数的步骤
问题:(1)函数y=f(x)在[x0,x0+Δx]的平均变化率为 ,你能说出它的几何意义吗?
表示过A(x0,f(x0))和B(x0+Δx,f(x0+Δx))两点的直线的斜率,这条直线称为曲线y=f(x)在点A处的一条割线.
(2)当Δx变化时,直线如何变化?
直线AB绕点A转动.
(3)当Δx→0时,直线变化到哪里?
直线过点A与曲线y=f(x)相切位置.
函数y=f(x)在x0处的导数f′(x0),是曲线y=f(x)在点(x0,f(x0))处的切线的斜率,函数y=f(x)在x0处切线的斜率反映了导数的几何意义.
思考1:如何求曲线f(x)在点(x0,f(x0))处的切线方程?
根据导数的几何意义,求出函数y=f(x)在点(x0,f(x0))处的导数,即曲线在该点处的切线的斜率,再由直线方程的点斜式求出切线方程.
思考2:曲线f(x)在点(x0,f(x0))处的切线与曲线过点(x0,y0)的切线有什么不同?
曲线f(x)在点(x0,f(x0))处的切线,点(x0,f(x0))一定是切点,只要求出k=f'(x0),利用点斜式写出切线方程即可;
而曲线f(x)过某点(x0,y0)的切线,给出的点(x0,y0)不一定在曲线上,即使在曲线上也不一定是切点.
思考3:曲线在某点处的切线是否与曲线只有一个交点?
不一定.曲线y=f(x)在点P(x0,f(x0))处的切线l与曲线y=f(x)的交点个数不一定只有一个,如图所示.
解:∵P(2,4)在曲线y=13x3+43上,
∴曲线在点P(2,4)处切线的斜率为
k=limΔ????→013(2+Δ????)3+43?13×23+43Δ????=limΔ????→04+2Δ????+13(Δ????)2=4.
∴曲线在点P(2,4)处的切线方程为y-4=4(x-2),
即4x-y-4=0.
?
例1 已知曲线y=13x3+43,求曲线在点P(2,4)处的切线方程.
?
变式:已知曲线y=13x3+43,求曲线过点P(2,4)处的切线方程.
?
解:设曲线y=13x3+43与过点P(2,4)的切线相切于点A????0,13????03+43,
则切线的斜率为k=limΔ????→013(????0+Δ????)3?13????03Δ????=????02,
∴切线方程为y-13????03+43=????02(x-x0),即y=????02·x-23????03+43.
∵点P(2,4)在切线上,∴4=2????02-23????03+43,即????03-3????02+4=0.
?
∴????03+????02-4????02+4=0,
∴????02(x0+1)-4(x0+1)(x0-1)=0,
∴(x0+1)(x0-2)2=0,
解得x0=-1或x0=2.
故所求的切线方程为x-y+2=0或4x-y-4=0.
?
变式:已知曲线y=13x3+43,求曲线过点P(2,4)处的切线方程.
?
1.求曲线在某点处的切线方程时,该点就是切点,因此可直接求出切线斜率,写出切线方程.
2.求过曲线上某点的切线方程时,要注意该点不一定是切点.因此,在解题时要先设出切点,再求出切线斜率,根据切点与斜率写出切线方程,最后将该点的坐标代入.在解题过程中不必考虑该点是否为切点.
归纳总结
例2 已知函数y1=f(x)=x2-1在x=x0处的切线与函数y2=g(x)=1-x3在x=x0处的切线互相平行,求x0的值.
方法总结
根据切线斜率求切点坐标的步骤
(1)设切点坐标(x0,y0).
(2)求导函数f'(x).
(3)求切线的斜率f'(x0).
(4)由斜率间的关系列出关于x0的方程,解方程求x0.
(5)点(x0,y0)在曲线f(x)上,将(x0,y0)代入求y0,得切点坐标.
借助曲线的切线,我们还可以从几何上来理解瞬时变化率的实际意义,并可以利用某一点的导数来估计这一点附近的函数值,具体过程如下.
如果函数????=????(????)在????0处的导数为????′(????0),且在????0处自变量的改变量为?????,对应的函数值改变量为
?????=????????0+??????????(????0),
则
????????0+?????=????????0+?????
?
此时曲线????=????(????)在????0处的切线l的斜率为????′(????0),因此
AC=?????,CD=????′(????0) ?????.
又因为BC=?y,可以看出,当?????很小时,?????可用????′(????0) ?????来近似表示,即
?y≈????′(????0)??????,
所以 ????????0+?????≈????????0+????′(????0)??????.
?
?????
?
本质上是用????=????0处的切线代替了????=????0附近的曲线????=????(????),使用了“以直代曲”的方法.
?
例3 已知f(x)=x2+1,利用f(1)=2,f'(1)=2,Δx=0.04,则f(1.04)的近似值为 .
2.08
解析:设x=x0+Δx,Δx=x-x0,
则有f(x)≈f(x0)+f'(x0)(x-x0),
所以f(1.04)≈f(1)+0.04f'(1)=2+0.04×2=2.08.
1.已知函数f(x)=?1????,则曲线y=f (x)在(1,-1)处的切线方程是( )
A.x-y-2=0 B.2x-2y+3=0
C.x+y=0 D.x-y=0
?
A
2.函数y=f(x)=2x2+4x在x=3处的导数为 .
3.曲线y=14x2在点Q(2,1)处的切线方程为 .
4.已知曲线y=f(x)=2x2+4x在点P处的切线斜率为16,则P点坐标为________.
?
16
x-y-1=0
(3,30)
根据今天所学,回答下列问题:
1.如何求函数在某点处的切线的方程?
2.如何根据切线斜率求切点坐标?
