6.2.1 课时1 利用导数判断函数的单调性 课件(16张PPT)
文档属性
| 名称 | 6.2.1 课时1 利用导数判断函数的单调性 课件(16张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-15 00:00:00 | ||
图片预览




文档简介
6.2.1 课时1
利用导数判断函数的单调性
人教B版(2019)选择性必修第三册
1.理解导数与函数单调性的关系.
2.会利用导数判断或证明函数单调性.
3.会利用导数求函数单调区间.
我们知道,对于函数y=f(x)来说,导数f?(x)刻画的是函数y=f(x)在点x的瞬时变化率,函数的单调性描述的是函数值y随自变量x取值的增加而增加,或函数值y随自变量x取值的增加而减少.两者都在刻画函数的变化,那么,导数与函数的单调性之间有何关系呢?
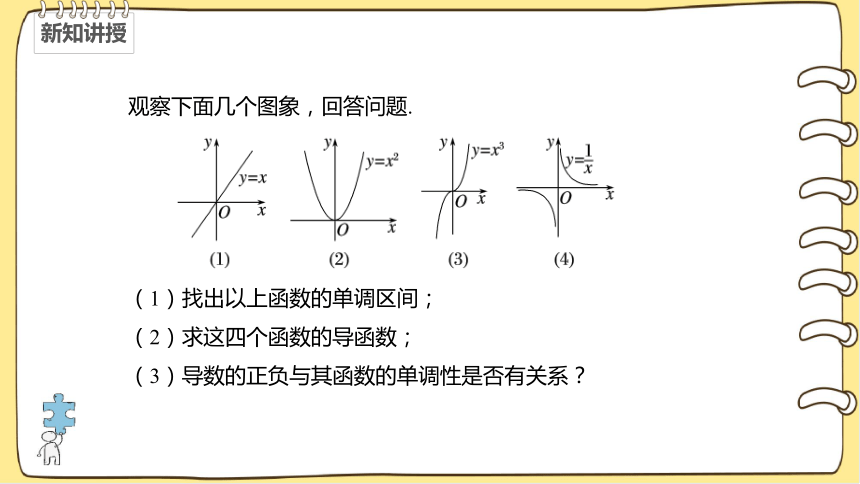
观察下面几个图象,回答问题.
(1)找出以上函数的单调区间;
(2)求这四个函数的导函数;
(3)导数的正负与其函数的单调性是否有关系?
{5940675A-B579-460E-94D1-54222C63F5DA}y=x
y=x2
y=x3
y=1????
增(-∞,+∞)
增(0,+∞)
减(0,+∞)
增(-∞,+∞)
减(-∞,0),(0,+∞)
y'=1
y'=2x
y'=3x2
y'=-1????2
y'>0?x∈R
y'>0?x>0
y'<0?x<0
y'≥0?x∈R
y'<0?x≠0
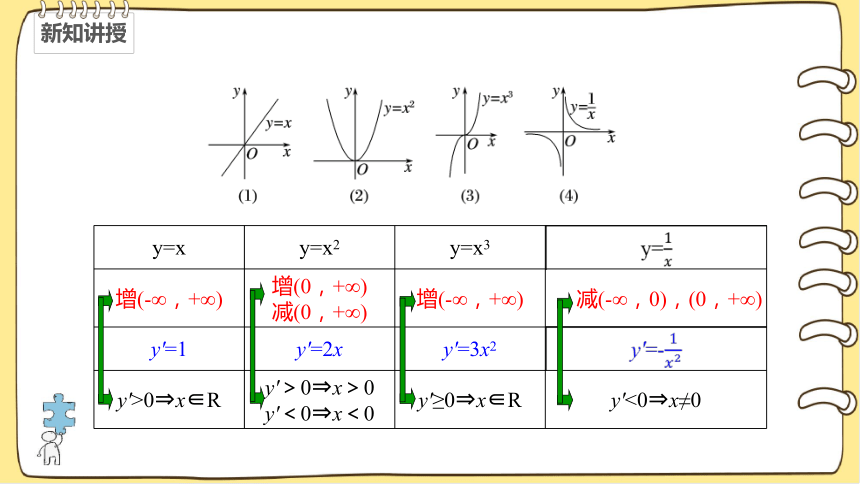
{5940675A-B579-460E-94D1-54222C63F5DA}y=x
y=x2
y=x3
增(-∞,+∞)
增(0,+∞)
减(0,+∞)
增(-∞,+∞)
减(-∞,0),(0,+∞)
y'=1
y'=2x
y'=3x2
y'>0?x∈R
y'>0?x>0
y'<0?x<0
y'≥0?x∈R
y'<0?x≠0
函数f (x)的单调性与导函数f ′(x)正负的关系
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A} f ′(x)的正负
f (x)的单调性
f ′(x)>0
单调递_____________
f ′(x)<0
单调递_____________
增
减
定义在区间(a,b)内的函数y=f (x):
注意:在某一区间内f'(x)>0(或f'(x)<0)是函数f(x)在该区间上为增(或减)函数的充分不必要条件.
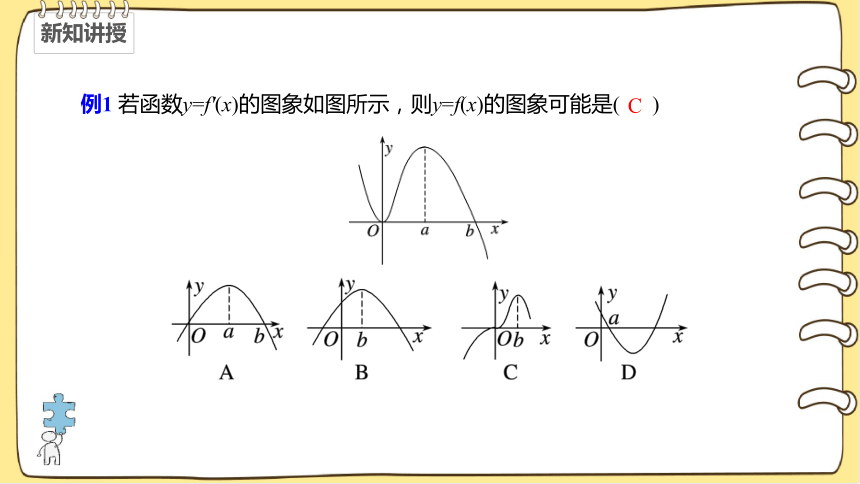
例1 若函数y=f'(x)的图象如图所示,则y=f(x)的图象可能是( )
C
解析:由y=f'(x)的图象可得,在(-∞,b)上f'(x)≥0,
在(b,+∞)上f'(x)<0,
根据原函数图象与导函数图象的关系可得,
y=f(x)在(-∞,b)上是增函数,在(b,+∞)上是减函数,可排除A,D,
且在x=0处,f'(x)=0,即在x=0处,y=f(x)的切线的斜率为0,可排除B,故选C.
√
变式:已知函数y=f(x)在定义域(-32,3)内可导,其图象如图所示.若y=f(x)的导函数为y=f'(x),则不等式f'(x)<0的解集为 .?
?
(-13,1)∪(2,3)
?
例2 求证:函数f(x)=ex-x-1在区间(0,+∞)内单调递增,在区间(-∞,0)内单调递减.
证:由f(x)=ex-x-1,得f'(x)=ex-1.
当x∈(0,+∞)时,ex>1,即f'(x)=ex-1>0,
故函数f(x)在区间(0,+∞)内单调递增;
当x∈(-∞,0)时,ex<1,即f'(x)=ex-1<0,
故函数f(x)在区间(-∞,0)内单调递减.
例3 利用导数判断下列函数的单调性:
(1)f(x)=13x3-x2+2x-5;(2)f(x)=x-1????-ln x;(3)f(x)=x-ex(x>0).
?
解:(1)因为f(x)=13x3-x2+2x-5,
所以f'(x)=x2-2x+2=(x-1)2+1>0,
所以函数f(x)=13x3-x2+2x-5在R上单调递增.
?
(2)f(x)=x-1????-ln x;(3)f(x)=x-ex(x>0).
?
(2)因为f(x)=x-1????-ln x,x∈(0,+∞),
所以f'(x)=1+1????2-1????=????2?????+1????2=?????122+34????2>0,
所以f(x)=x-1????-ln x在(0,+∞)上单调递增.
(3)因为f(x)=x-ex,x∈(0,+∞),且f'(x)=1-ex<0,
所以f(x)=x-ex在(0,+∞)上单调递减.
?
方法归纳
判定函数单调性的步骤:
① 求出函数的定义域;
② 求出函数的导数f ?(x);
③ 判定导数f ?(x)的符号;
④ 确定函数f(x)的单调性.
1. 函数????????=2??????????????????????在(?∞,+∞)上是( )
A.增函数 B.减函数 C.先增后减 D.不确定
?
A
2. 函数????=????(????)的图像如图所示,则下列正确的是( )
A. ????′3>0
B. ????′3<0
C. ????′3=0
D. ????′3的正负不确定
?
B
3. 函数f(x)=3+xln x的单调递增区间是( )
C
4.函数f (x)=ex-x的单调递增区间为____________.
(0,+∞)
根据今天所学,回答下列问题:
1.导数的符号与函数的单调性之间的关系?
2.怎样判断函数的单调性?
利用导数判断函数的单调性
人教B版(2019)选择性必修第三册
1.理解导数与函数单调性的关系.
2.会利用导数判断或证明函数单调性.
3.会利用导数求函数单调区间.
我们知道,对于函数y=f(x)来说,导数f?(x)刻画的是函数y=f(x)在点x的瞬时变化率,函数的单调性描述的是函数值y随自变量x取值的增加而增加,或函数值y随自变量x取值的增加而减少.两者都在刻画函数的变化,那么,导数与函数的单调性之间有何关系呢?
观察下面几个图象,回答问题.
(1)找出以上函数的单调区间;
(2)求这四个函数的导函数;
(3)导数的正负与其函数的单调性是否有关系?
{5940675A-B579-460E-94D1-54222C63F5DA}y=x
y=x2
y=x3
y=1????
增(-∞,+∞)
增(0,+∞)
减(0,+∞)
增(-∞,+∞)
减(-∞,0),(0,+∞)
y'=1
y'=2x
y'=3x2
y'=-1????2
y'>0?x∈R
y'>0?x>0
y'<0?x<0
y'≥0?x∈R
y'<0?x≠0
{5940675A-B579-460E-94D1-54222C63F5DA}y=x
y=x2
y=x3
增(-∞,+∞)
增(0,+∞)
减(0,+∞)
增(-∞,+∞)
减(-∞,0),(0,+∞)
y'=1
y'=2x
y'=3x2
y'>0?x∈R
y'>0?x>0
y'<0?x<0
y'≥0?x∈R
y'<0?x≠0
函数f (x)的单调性与导函数f ′(x)正负的关系
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A} f ′(x)的正负
f (x)的单调性
f ′(x)>0
单调递_____________
f ′(x)<0
单调递_____________
增
减
定义在区间(a,b)内的函数y=f (x):
注意:在某一区间内f'(x)>0(或f'(x)<0)是函数f(x)在该区间上为增(或减)函数的充分不必要条件.
例1 若函数y=f'(x)的图象如图所示,则y=f(x)的图象可能是( )
C
解析:由y=f'(x)的图象可得,在(-∞,b)上f'(x)≥0,
在(b,+∞)上f'(x)<0,
根据原函数图象与导函数图象的关系可得,
y=f(x)在(-∞,b)上是增函数,在(b,+∞)上是减函数,可排除A,D,
且在x=0处,f'(x)=0,即在x=0处,y=f(x)的切线的斜率为0,可排除B,故选C.
√
变式:已知函数y=f(x)在定义域(-32,3)内可导,其图象如图所示.若y=f(x)的导函数为y=f'(x),则不等式f'(x)<0的解集为 .?
?
(-13,1)∪(2,3)
?
例2 求证:函数f(x)=ex-x-1在区间(0,+∞)内单调递增,在区间(-∞,0)内单调递减.
证:由f(x)=ex-x-1,得f'(x)=ex-1.
当x∈(0,+∞)时,ex>1,即f'(x)=ex-1>0,
故函数f(x)在区间(0,+∞)内单调递增;
当x∈(-∞,0)时,ex<1,即f'(x)=ex-1<0,
故函数f(x)在区间(-∞,0)内单调递减.
例3 利用导数判断下列函数的单调性:
(1)f(x)=13x3-x2+2x-5;(2)f(x)=x-1????-ln x;(3)f(x)=x-ex(x>0).
?
解:(1)因为f(x)=13x3-x2+2x-5,
所以f'(x)=x2-2x+2=(x-1)2+1>0,
所以函数f(x)=13x3-x2+2x-5在R上单调递增.
?
(2)f(x)=x-1????-ln x;(3)f(x)=x-ex(x>0).
?
(2)因为f(x)=x-1????-ln x,x∈(0,+∞),
所以f'(x)=1+1????2-1????=????2?????+1????2=?????122+34????2>0,
所以f(x)=x-1????-ln x在(0,+∞)上单调递增.
(3)因为f(x)=x-ex,x∈(0,+∞),且f'(x)=1-ex<0,
所以f(x)=x-ex在(0,+∞)上单调递减.
?
方法归纳
判定函数单调性的步骤:
① 求出函数的定义域;
② 求出函数的导数f ?(x);
③ 判定导数f ?(x)的符号;
④ 确定函数f(x)的单调性.
1. 函数????????=2??????????????????????在(?∞,+∞)上是( )
A.增函数 B.减函数 C.先增后减 D.不确定
?
A
2. 函数????=????(????)的图像如图所示,则下列正确的是( )
A. ????′3>0
B. ????′3<0
C. ????′3=0
D. ????′3的正负不确定
?
B
3. 函数f(x)=3+xln x的单调递增区间是( )
C
4.函数f (x)=ex-x的单调递增区间为____________.
(0,+∞)
根据今天所学,回答下列问题:
1.导数的符号与函数的单调性之间的关系?
2.怎样判断函数的单调性?
