6.2.2 课时2 函数的最值求法 课件(18张PPT)
文档属性
| 名称 | 6.2.2 课时2 函数的最值求法 课件(18张PPT) |
|
|
| 格式 | pptx | ||
| 文件大小 | 632.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-04-15 16:54:27 | ||
图片预览






文档简介
(共18张PPT)
6.2.2 课时2
函数的最值求法
人教B版(2019)选择性必修第三册
1.理解函数最值的概念,了解其与函数极值的区别与联系.
2.会求某闭区间上函数的最值.
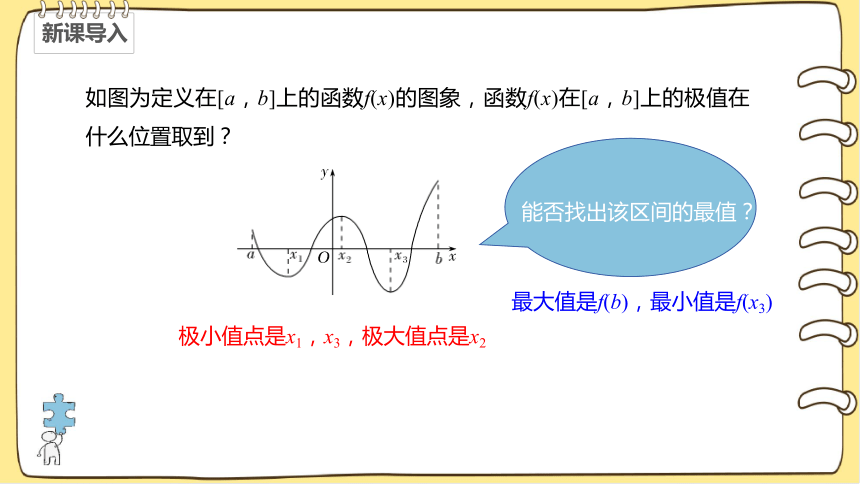
如图为定义在[a,b]上的函数f(x)的图象,函数f(x)在[a,b]上的极值在什么位置取到?
极小值点是x1,x3,极大值点是x2
能否找出该区间的最值?
最大值是f(b),最小值是f(x3)
函数的最值
(1)一般地,如果函数y=f (x)在定义域内的每一点都可导,且函数存在最值,则函数的最值点一定是某个极值点;
(2)如果函数y=f (x)的定义域为[a,b] 且存在最值,函数y=f (x)在(a,b)内可导,那么函数的最值点要么是区间端点a或b,要么是极值点.
讨论:函数的极值与最值的区别是什么?
函数的最大值和最小值是一个整体性概念,最大(小)值是比较整个定义区间的函数值得出的,函数的极值是比较极值点附近的函数值得出的,
函数的极值可以有多个,但最值只能有一个;
极值只能在区间内取得,最值则可以在端点取得;
有极值的未必有最值,有最值的未必有极值;
极值有可能成为最值,最值只要不在端点必定是极值.
注意:1.给定的区间必须是闭区间,如果是开区间,尽管函数图象是连续的,那么它也不一定有最大值和最小值.
例如函数f(x)=在区间(0,2)上的图象是连续不断的曲线,但在该区间上,
函数f(x)既没有最大值,也没有最小值.
2.所给函数的图象必须是连续曲线,否则不一定有最值.
例如函数f(x)=在[-1,1]上只有最大值,而没有
最小值.
3.函数的最值是一个整体性概念,最大值(最小值)必须是整个区间内所有函数值中的最大值(最小值).函数在闭区间上若存在最大值或最小值,则最大值或最小值只能各有一个,具有唯一性;而极大值和极小值可能有多个,也可能没有.
4.极值只能在函数区间的内部取得,而最值可以在区间的端点取得,有极值的不一定有最值,有最值的不一定有极值,极值有可能是最值,最值只要不在端点处则一定是极值.
例1 求函数f(x)=x3-x2+5在区间[-2,2]上的最大值与最小值.
解:f'(x)=3x2-x-2,令f'(x)=0,得x1=-,x2=1.
当x变化时,f'(x),f(x)的变化情况如下表:
x -2 (-2,-) - (-,1) 1 (1,2) 2
f'(x) + 0 - 0 +
f(x) -1 ↗ 极大值 ↘ 极小值 ↗ 7
通过比较,f(x)max=f(2)=7,f(x)min=f(-2)=-1.
方法归纳
求函数 y = f (x) 在区间 [a,b] 上的最值的步骤:
例2 已知h(x)=x3+3x2-9x+1在区间[k,2]上的最大值是28,求k的取值范围.
解:h(x)=x3+3x2-9x+1,h'(x)=3x2+6x-9.
令h'(x)=0,解得x1=-3,x2=1,
当x变化时,h'(x)及h(x)的变化情况如下表:
x (-∞,-3) -3 (-3,1) 1 (1,+∞)
h'(x) + 0 - 0 +
h(x) ↗ 28 ↘ -4 ↗
当x=-3时,h(x)取极大值28;当x=1时,h(x)取极小值-4.
而h(2)=3∴如果h(x)在区间[k,2]上的最大值为28,则k≤-3.
即k的取值范围为(-∞,-3].
例2 已知h(x)=x3+3x2-9x+1在区间[k,2]上的最大值是28,求k的取值范围.
已知函数在某区间上的最值求参数的值(范围)是求函数最值的逆向思维,一般先求导数,利用导数研究函数的单调性及极值点,探索最值点,根据已知最值列方程(不等式)解决问题.其中注意分类讨论思想的应用.
方法归纳
例3 设函数f(x)=tx2+2t2x+t-1(x∈R,t>0),h(t)为f(x)的最小值.
(1)求h(t);
(2)若h(t)<-2t+m对t∈(0,2)恒成立,求实数m的取值范围.
解:(1)∵f(x)=t(x+t)2-t3+t-1(x∈R,t>0),
∴当x=-t时,f(x)取最小值f(-t)=-t3+t-1,
即h(t)=-t3+t-1.
(2)若h(t)<-2t+m对t∈(0,2)恒成立,求实数m的取值范围.
(2)令g(t)=h(t)-(-2t+m)=-t3+3t-1-m,
由g'(t)=-3t2+3=0,得t=1,t=-1(不合题意,舍去).
当t变化时,g'(t),g(t)的变化情况如下表:
t (0,1) 1 (1,2)
g'(t) + 0 -
g(t) ↗ 1-m ↘
∴g(t)在(0,2)内有最大值g(1)=1-m.
h(t)<-2t+m在(0,2)内恒成立等价于g(t)<0在(0,2)内恒成立,
即等价于1-m<0,
∴m的取值范围为(1,+∞).
分离参数法求解不等式恒成立问题的步骤
方法归纳
1.下列结论正确的是( )
A.若f(x)在[a,b]上有极大值,则极大值一定是[a,b]上的最大值
B.若f(x)在[a,b]上有极小值,则极小值一定是[a,b]上的最小值
C.若f(x)在[a,b]上有极大值,则极小值一定是在x=a和x=b处取得
D.若f(x)在[a,b]上连续,则f(x)在[a,b]上存在最大值和最小值
D
2.函数f(x)=x3-3x+1在闭区间[-3,0]上的最大值和最小值分别是( )
A.1,-1 B.1,-17
C.3,-17 D.9,-19
3.已知函数f(x)=x4-2x3+3m,x∈R,若f(x)+9≥0恒成立,则实数m的取值范围
是 .
C
[,+∞)
6.2.2 课时2
函数的最值求法
人教B版(2019)选择性必修第三册
1.理解函数最值的概念,了解其与函数极值的区别与联系.
2.会求某闭区间上函数的最值.
如图为定义在[a,b]上的函数f(x)的图象,函数f(x)在[a,b]上的极值在什么位置取到?
极小值点是x1,x3,极大值点是x2
能否找出该区间的最值?
最大值是f(b),最小值是f(x3)
函数的最值
(1)一般地,如果函数y=f (x)在定义域内的每一点都可导,且函数存在最值,则函数的最值点一定是某个极值点;
(2)如果函数y=f (x)的定义域为[a,b] 且存在最值,函数y=f (x)在(a,b)内可导,那么函数的最值点要么是区间端点a或b,要么是极值点.
讨论:函数的极值与最值的区别是什么?
函数的最大值和最小值是一个整体性概念,最大(小)值是比较整个定义区间的函数值得出的,函数的极值是比较极值点附近的函数值得出的,
函数的极值可以有多个,但最值只能有一个;
极值只能在区间内取得,最值则可以在端点取得;
有极值的未必有最值,有最值的未必有极值;
极值有可能成为最值,最值只要不在端点必定是极值.
注意:1.给定的区间必须是闭区间,如果是开区间,尽管函数图象是连续的,那么它也不一定有最大值和最小值.
例如函数f(x)=在区间(0,2)上的图象是连续不断的曲线,但在该区间上,
函数f(x)既没有最大值,也没有最小值.
2.所给函数的图象必须是连续曲线,否则不一定有最值.
例如函数f(x)=在[-1,1]上只有最大值,而没有
最小值.
3.函数的最值是一个整体性概念,最大值(最小值)必须是整个区间内所有函数值中的最大值(最小值).函数在闭区间上若存在最大值或最小值,则最大值或最小值只能各有一个,具有唯一性;而极大值和极小值可能有多个,也可能没有.
4.极值只能在函数区间的内部取得,而最值可以在区间的端点取得,有极值的不一定有最值,有最值的不一定有极值,极值有可能是最值,最值只要不在端点处则一定是极值.
例1 求函数f(x)=x3-x2+5在区间[-2,2]上的最大值与最小值.
解:f'(x)=3x2-x-2,令f'(x)=0,得x1=-,x2=1.
当x变化时,f'(x),f(x)的变化情况如下表:
x -2 (-2,-) - (-,1) 1 (1,2) 2
f'(x) + 0 - 0 +
f(x) -1 ↗ 极大值 ↘ 极小值 ↗ 7
通过比较,f(x)max=f(2)=7,f(x)min=f(-2)=-1.
方法归纳
求函数 y = f (x) 在区间 [a,b] 上的最值的步骤:
例2 已知h(x)=x3+3x2-9x+1在区间[k,2]上的最大值是28,求k的取值范围.
解:h(x)=x3+3x2-9x+1,h'(x)=3x2+6x-9.
令h'(x)=0,解得x1=-3,x2=1,
当x变化时,h'(x)及h(x)的变化情况如下表:
x (-∞,-3) -3 (-3,1) 1 (1,+∞)
h'(x) + 0 - 0 +
h(x) ↗ 28 ↘ -4 ↗
当x=-3时,h(x)取极大值28;当x=1时,h(x)取极小值-4.
而h(2)=3
即k的取值范围为(-∞,-3].
例2 已知h(x)=x3+3x2-9x+1在区间[k,2]上的最大值是28,求k的取值范围.
已知函数在某区间上的最值求参数的值(范围)是求函数最值的逆向思维,一般先求导数,利用导数研究函数的单调性及极值点,探索最值点,根据已知最值列方程(不等式)解决问题.其中注意分类讨论思想的应用.
方法归纳
例3 设函数f(x)=tx2+2t2x+t-1(x∈R,t>0),h(t)为f(x)的最小值.
(1)求h(t);
(2)若h(t)<-2t+m对t∈(0,2)恒成立,求实数m的取值范围.
解:(1)∵f(x)=t(x+t)2-t3+t-1(x∈R,t>0),
∴当x=-t时,f(x)取最小值f(-t)=-t3+t-1,
即h(t)=-t3+t-1.
(2)若h(t)<-2t+m对t∈(0,2)恒成立,求实数m的取值范围.
(2)令g(t)=h(t)-(-2t+m)=-t3+3t-1-m,
由g'(t)=-3t2+3=0,得t=1,t=-1(不合题意,舍去).
当t变化时,g'(t),g(t)的变化情况如下表:
t (0,1) 1 (1,2)
g'(t) + 0 -
g(t) ↗ 1-m ↘
∴g(t)在(0,2)内有最大值g(1)=1-m.
h(t)<-2t+m在(0,2)内恒成立等价于g(t)<0在(0,2)内恒成立,
即等价于1-m<0,
∴m的取值范围为(1,+∞).
分离参数法求解不等式恒成立问题的步骤
方法归纳
1.下列结论正确的是( )
A.若f(x)在[a,b]上有极大值,则极大值一定是[a,b]上的最大值
B.若f(x)在[a,b]上有极小值,则极小值一定是[a,b]上的最小值
C.若f(x)在[a,b]上有极大值,则极小值一定是在x=a和x=b处取得
D.若f(x)在[a,b]上连续,则f(x)在[a,b]上存在最大值和最小值
D
2.函数f(x)=x3-3x+1在闭区间[-3,0]上的最大值和最小值分别是( )
A.1,-1 B.1,-17
C.3,-17 D.9,-19
3.已知函数f(x)=x4-2x3+3m,x∈R,若f(x)+9≥0恒成立,则实数m的取值范围
是 .
C
[,+∞)
