北师大八下4.3.2公式法（2）

第四章 因式分解
4.3.2公式法（2）
北师大版 数学 八年级 下册
学习目标
1．理解完全平方公式，弄清完全平方公式的形式和特点。
2．掌握运用完全平方公式分解因式的方法，能正确运用完全平方公式把多项式分解因式。
情景导入
1.因式分解的概念是什么？
把一个多项式化成几个整式的积的形式，叫做因式分解.
3.完全平方公式的内容是什么？
提公因式法，利用平方差公式逆向变形
2.我们学过了哪些因式分解的方法？
(a±b)2=a2±2ab+b2.
核心知识点一：
用完全平方公式分解因式
多项式a2+2ab+b2与a2-2ab+b2有什么特点？你能试着将它们分解因式吗？
a2+2ab+b2
=a2+ab+ab+b2
=a(a+b)+b(a+b)
=(a+b)(a+b)
a2-2ab+b2
=a2-ab-ab+b2
=a(a-b)-b(a-b)
=(a-b)(a-b)
=(a+b)2
=(a-b)2
提公因式
提公因式
探索新知
现在我们把完全平方公式反过来，可得：
两个数的平方和，加上 这两个数的积的两倍，等于这两数和 的平方．
完全平方公式：
（或减去）
（或者差）
探索新知
归纳总结
定义：由两个数的平方加上或减去两个数的积的2倍构成的多项式叫做完全平方式.
a2+2ab+b2
a2-2ab+b2
=(a+b)2
=(a-b)2
1、含有三项；
2、其中两项可写成两数的平方和的形式，另一项刚好是两项积的2倍；
3、a和b即可以是数，也可以是单项式或多项式.
完全平方式的特点：
探索新知
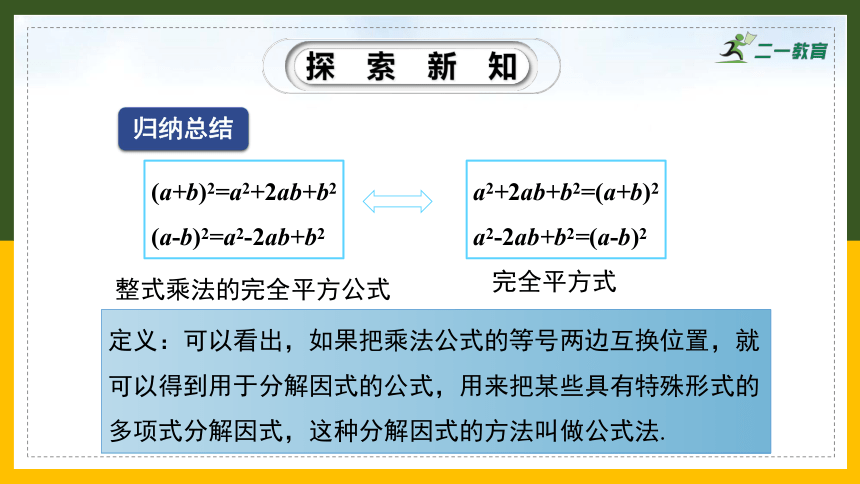
整式乘法的完全平方公式
(a+b)2=a2+2ab+b2
(a-b)2=a2-2ab+b2
a2+2ab+b2=(a+b)2
a2-2ab+b2=(a-b)2
完全平方式
定义：可以看出，如果把乘法公式的等号两边互换位置，就可以得到用于分解因式的公式，用来把某些具有特殊形式的多项式分解因式，这种分解因式的方法叫做公式法.
归纳总结
探索新知
练一练：
1.请你来判断，下列各式是不是完全平方式？若不是，请说明原因
（1）a2－4a+4;
（2）1+4a?;
（3）4b2+4b-1;
（4）x2+x+0.25.

是
（2）因为它只有两项；
不是
（3）4b?与-1的符号不统一；
不是
是
探索新知
（3）a?+4ab+4b?=( )?+2· ( ) ·( )+( )?=( )?
（2）m?－6m+9=( )? － 2· ( ) ·( )+( )? =( )?
（1） x?+4x+4= ( )? +2·( )·( )+( )? =( )?
x
2
x + 2
a
a 2b
a + 2b
2b
2.对照 a?±2ab+b?=(a±b)?，填空：
m
m - 3
3
x
2
m
3
探索新知
例1： 分解因式：
（1）16x2+24x+9； （2）-x2+4xy-4y2.
分析：(1)中，16x2 + 24x +9= (4x)2+ 2·4x·3 + (3)2.
2
a
b
+b2
a2
(2)中首项有负号，先提取负号，注意各项要变号。先变形为-(x2-4xy+4y2)
解： (1)16x2+ 24x +9
= (4x + 3)2；
= (4x)2 + 2·4x·3 + (3)2
(2)-x2+ 4xy-4y2
=-(x2-4xy+4y2)
=-(x-2y)2.
探索新知
例2： 把下列各式分解因式：
(1)3ax2+6axy+3ay2 ； (2)(a+b)2-12(a+b)+36.
解: (1)原式=3a(x2+2xy+y2)
=3a(x+y)2；
分析：(1)中有公因式3a,应先提出公因式，再进一步分解因式；
(2)中将a+b看成一个整体，设a+b=m,则原式化为m2-12m+36.
(2)原式=(a+b)2-2·(a+b) ·6+62
=(a+b-6)2.
探索新知
例3： 利用因式分解计算：
(1)20202－2×2020×2019+2019? (2)742＋74×52＋262
=(2020-2019)?
＝(74＋26)2
=1.
＝10000.
解：20202－2×2020×2019+2019?
解：742＋74×52＋262
＝742＋74×26×2＋262
探索新知
例4：已知ab=2，a+b=5，求a3b+2a2b2+ab3的值.
解：a3b+2a2b2+ab3
=ab(a2+2ab+b2)
=ab(a+b)2.
当ab=2，a+b=5时，
a3b+2a2b2+ab3
=2×52
=50.
探索新知
1.注意多项式的形式是否符合公式的形式；
2.因式分解过程中或分解后可能要进行整式的乘法运算或幂的运算.
3.当多项式的各项含有公因式时，通常先提公因式，如何再进一步因式分解.
利用公式法分解因式的注意事项有哪些？
归纳总结
探索新知
归纳总结
因式分解的一般方法与步骤
方法
①提公因式法：ma＋mb＋mc＝m(a＋b＋c);
②公式法：
?
步骤
①有公因式时，先提公因式;
②没有公因式时，考虑是否符合公式的特征，能否用公式法分解;
③有些问题中提公因式后还能用公式，有些问题中用完公式后还能再用公式;
④因式分解要彻底，分解到不能再分解为止
探索新知
当堂检测
1.下列多项式中，能分解因式的是( ) .
A
A． ?a2+4b2 B． ?a2?b2 C． x4?4x2?4 D． a2?ab+b2
?
2.下列多项式中，能运用公式法进行因式分解的是( ) .
C
A． a2+b2 B． x2+9
C． m2?n2 D． x2+2xy+4y2
?
当堂检测
3.下列多项式能用完全平方公式分解因式的是( ) .
D
A． x2?6x?9 B． a2?16a+32
C． x2?2xy+4y2 D． 9a2?6a+1
?
4.把多项式 x2?6x+9 分解因式，结果正确的是( ) .
?
A
A． x?32 B． x?92
C． x+3x?3 D． x+9x?9
?
当堂检测
5.多项式 2x3?4x2+2x 因式分解为( ) .
?
A
A． 2xx?12 B． 2xx+12 C． x2x?12 D． x2x+12
?
6.把 a2+12? 4a2 分解因式得( ) .
?
C
A． a2+1?4a2 B． a2+1+2aa2+1?2a
C． a+12a?12 D． a2?12
?
当堂检测
8.已知 a=b+2 ，则代数式 3a2?6ab+3b2+2?022 的值为( ).
A.2020 B.2024 C.2021 D.2034
?
7.已知 a+b=3 ， ab=1 ，则多项式 a2b+ab2?a?b 的值为( ).
A.－1 B. 0 C. 3 D. 6
?
B
D
当堂检测
9.已知 x2?4x+y2?6y+13=0 ，求 x ， y 的值.
?
解：
∵x2?4x+y2?6y+13
=x2?4x+4+y2?6y+9
=x?22+y?32
=0 ，
∴x?2=0 ， y?3=0 ，解得 x=2 ， y=3 .
?
当堂检测
10.利用因式分解简便计算.
（1）1242×25－25×762；
解： （1）1242×25－25×762＝25×（1242－762）
＝25×（124＋76）×（124－76）
＝25×200×48
＝5 000×48
＝240 000.
当堂检测
10.利用因式分解简便计算.
（2）382＋24×38＋144.
解： （2）382＋24×38＋144
＝382＋2×12×38＋122
＝（38＋12）2
＝502
＝2 500.
当堂检测
11．(1)若实数a，b满足(a-1)2＋(a+2b)2＝0，求a，b的值；
(2)根据(1)的解题思路解决问题：若实数x，y满足x2＋4x＋4y2－4y＋5＝0，求x，y的值．
解：(1)∵(a－1)2＋(a+2b)2＝0，∴a－1＝0，a＋2b＝0，∴a＝1，b＝－12.
?
(2)∵x2＋4x＋4y2－4y＋5＝0，
∴x2＋4x＋4＋4y2－4y＋1＝0，
∴（x+2）2＋(2y-1)2＝0，
∴x＋2＝0，2y－1＝0，
∴x＝－2，y＝12.
?
一、利用公式法对多项式的因式分解.
a2±2ab+b2=(a±b)2.
二、利用公式法分解因式的注意事项
1.注意多项式的形式是否符合公式的形式；
2.因式分解过程中或分解后可能要进行整式的乘法运算或幂的运算.
3.当多项式的各项含有公因式时，通常先提公因式，如何再进一步因式分解.
感谢收看