北师大八下4.2.1提公因式法（1）

第四章 因式分解
4.2.1提公因式法（1）
北师大版 数学 八年级 下册
学习目标
1．经历探索分解因式方法的过程，体会数学知识之间的整体（整式乘法与因式分解）联系。
2．了解因式分解的意义，会用提公因式法进行因式分解。
情景导入
把一个多项式变成几个整式相乘的积的形式，这种变形叫做因式分解.
1.因式分解的概念
2.乘法分配律及其逆运算
a(b+c)=ab+ac
ab+ac=a(b+c)
核心知识点一：
确定公因式
观察下面的计算过程：
解：原式
你知道小明这么做的理由吗？
方法：他先找到各项中相同的因数，再逆用乘法分配律
38×57+38×43
?
=38×（57+43）
?
=38×100
?
=3800
?
公因数
探索新知
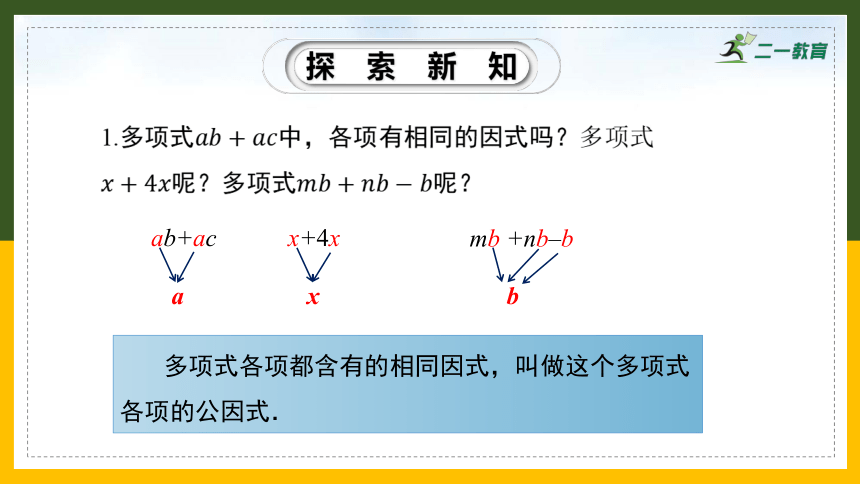
1.多项式????????+????????中，各项有相同的因式吗？多项式?
????+4????呢？多项式????????+?????????????呢？
?
多项式各项都含有的相同因式，叫做这个多项式各项的公因式．
ab+ac
x+4x
mb +nb–b
a
x
b
探索新知
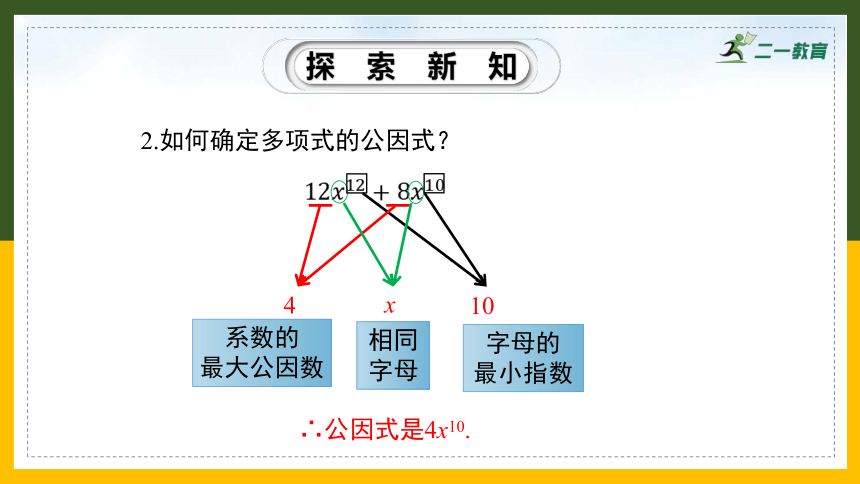
2.如何确定多项式的公因式？
12????12+8????10
?
4
x
10
系数的
最大公因数
相同字母
字母的
最小指数
∴公因式是4x10.
探索新知
归纳总结
确定公因式要从系数、字母及相同字母的指数三方面入手
1.系数：各项系数（包括常数项）的最大公因数；
2.字母：各项相同的字母（或相同因式）；
3.字母指数：取各相同字母（或相同因式）的最小指数.
探索新知
练一练：找出下列各式的公因式.
(1) 4x3+ 12x2;
(2) 3a- 9ab;
(3) -2a4+ a2b3-a3c;
(4) 2x2y3z5-6xy2z4+ 4x3y4z3;
(1)4x2,
(2)3a,
(3)a2,
(4)2xy2c3
探索新知
核心知识点二：
提公因式为单项式的因式分解
利用乘法分配律的逆运算，你可以将含有公因式的多项式进行因式分解吗？
ab+ac=a(b+c)
解：4x3+ 12x2
=4x2?x+4x2?3
=4x2(x2+3)
将多项式4x3+ 12x2分解因式
探索新知
上面利用乘法分配律的逆运算是把一个含有公因式的多项式进行因式分解的一种方法，这种方法叫做提公因式法.
如果一个多项式的各项含有公因式，那么就可以把这个公因式提出来，从而将多项式化成两个因式乘积的形式.这种因式分解的方法叫做提公因式法.
( a+b+c )
pa+ pb +pc
p
=
探索新知
例 ： 分解因式：
8a 3b 2 + 12ab 3c；
分析：提公因式法步骤（分两步）
第一步:找出公因式；
第二步:提取公因式 ，即将多项式化为两个因式的乘积。
解：8a3b2 + 12ab3c
=4ab2 ·2a2+4ab2 ·3bc
=4ab2(2a2+3bc)；
探索新知
提公因式法的步骤：
提公因式法因式分解的步骤：
第一步，找出公因式；
第二步，提取公因式，即用公因式去除这个多项式,所得的商式作为另一个因式；
第三步，分解因式，将多项式化为两个因式的积.
归纳总结
探索新知
用提公因式法分解因式应注意哪些问题呢？
解：?(1)3????+????3
=?????3+?????????2
=????3+????2；
?
例：把下列各式因式分解：
(1)3????+????3; (2)7????3?21????2；
?
(2)7????3?21????2
=7????2??????7????2?3
=7????2??????3；
?
注意：公因式要提尽.
易错点1：因式分解时分解不彻底.
探索新知
用提公因式法分解因式应注意哪些问题呢？
(3)8????3????2?12????????3????+????????；
?
解：(3) 8????3????2?12????????3????+????????
=?????????8????2??????????????12????2????+?????????1
=????????8????2?????12????2????+1；
?
注意：当多项式的某一项和公因式相同时，提公因式后剩余的项是1.
易错点2：提公因式时漏项.
探索新知
用提公因式法分解因式应注意哪些问题呢？
(4)?24????3+12????2?28????.
?
解：(4) ?24????3+12????2?28????
=?(24????3?12????2+28????)
=?(4?????6????2?4?????3????+4?????7)
=?4????(6????2?3????+7).
?
注意：当多项式第一项的系数是负数时，通常先提出“-”号，使括号内第一项的系数成为正数.在提出“-”号时，多项式的各项都要变号.
易错点3：提取“-”号时，括号内变错符号.
探索新知
当堂检测
1．用提公因式法分解因式正确的是( )
A．12abc－9a 2b 2c 2＝3abc (4－3ab)
B．3x 2y－3xy＋6y＝3y（x 2－x＋2y）
C．－a 2＋ab－ac＝－a (a－b＋c)
D．x 2y＋5xy－y＝y （x 2＋5x）
C
当堂检测
2.把多项式2x 2－4x 分解因式，应提取的公因式是( )
A．x　 　 B．2　　 C．x 2　 　 D．2x
D
3．多项式－9x 2y＋3xy 2－6xyz 中，各项的公因式是( )
A．－3xy　 B．3yz　 C．3xz　 D．－3x
A
当堂检测
4.已知ab＝6，a＋b＝7，那么代数式a 2b＋ab 2的值为( )
A．6　　 B．7　　　 C．13　　 D．42
D
5．把多项式a2＋2a 分解因式得( )
A．a(a＋2)　　 B．a(a－2)　　 C．(a＋2)2　　 D．(a＋2)(a－2)
A
当堂检测
6．如图，长为a，宽为b 的长方形周长为20，面积为16，则
a2b＋ab2的值为( )
A．80　 　 B．160　 　 C．320　 　 D．480
B
当堂检测
7．已知m 2－3m 的值为5，那么代数式2 030－2m 2＋6m 的值是( )
A．2 030　　 B．2 020　　 C．2 010　　 D．2 000
B
8.计算(－2)2 020＋(－2)2 021所得的结果是( )
A．－22 020　　 B．－22 021　　 C．22 020　　 D．－2
A
当堂检测
10．已知x＝3－2，y＝3＋2，则xy 2－x 2y 的值是 ．
?
22
?
11．2 0232－2 023×2 022＝ ．
2 023
9．若m 2＋m－1＝0，则m 3＋2m 2＋2 021的值是 ．
2 022
当堂检测
12．将下列各式进行因式分解：
(1)4xy 2＋6x 2y－2xy ;
(2)－8x 4y＋6x 3y 2－2x 3y.
解：4xy 2＋6x 2y－2xy＝2xy（2y＋3x－1）.
解：－8x 4y＋6x 3y 2－2x 3y＝－2x 3y（4x－3y＋1）.
当堂检测
13.先化简，再求值：（?????????)2+(?????????)(????+????)÷x，其中x＝－1，y＝12.
?
解：（?????????)2+(?????????)(????+????)÷x
＝(x－y)(x－y＋x＋y)÷x
＝2x(x－y)÷x
＝2(x－y)．
当 x＝－1，y＝12 时，
原式＝2(x－y)＝2×(-1-12)＝－3.
?
一.什么是提公因式法？
如果一个多项式的各项含有公因式，那么就可以把这个公因式提出来，从而将多项式化成两个因式乘积的形式.这种因式分解的方法叫做提公因式法.
2.不能只对式子的一部分题提公因式；
1.首项系数是负数时通常先提“-”号；
二.注意事项：
3.当某项与公因式相同时， 提公因式后这项为1，不能漏掉;
感谢收看